之前有和大家聊过光场相机的空域重聚焦原理,而我们知道对于信号处理而言,频域处理也是很常见的。对于光场重聚焦如何在频域进行表征呢?
Ng最早提出了频率域重对焦图像算法,算法核心是围绕傅里叶切片定理进行展开。我们知道傅里叶切片定理最重要的作用就是降维,对于四维光场数据为了方便对多维数据处理,首先需要将二维傅里叶切片定理延展至多维,然后降维至四维进行四维光场数据处理,就可以实现在频率域对光场重聚焦图像的处理。
由二维傅里叶切片定理可知:物体f(x,y)在角度θ下的平行投影的傅里叶变换,等于在同一角度下进行f(x,y)二维傅里叶变换的一条直线。假设f(x,y)平行于y轴可以得到一次投影,表示为:h(x,0)
其中
对上式进行傅里叶变换可得:
如果原函数f(x,y)进行傅里叶变换,当V=0时,可得
由上述推导可以知道傅里叶切片定理表明二维函数在一维方向上积分投影的傅里叶变换等于该二维函数傅里叶变换的一维切片。
将傅里叶切片定理推广至N维空间:设f是N维函数,对f进行坐标变换后将其积分投影至M维进行傅里叶变换,那么这个变换等于对函数求傅里叶变换,然后进行坐标逆变换,最后取该变换的M维切片,用算子简化表示如下:
其中
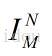
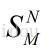
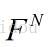
之前我们知道重聚焦空域表达式为:
结合上述两式进行变换后可以得到:
其中Bα表示坐标变换矩阵:由重聚焦的空域变换可以知道变换前后(u,v,s,t)=Bα(u,v,s',t')
由上面的推导我们得到傅里叶切片成像定理:传统图像是光场的四维傅里叶变换的二维切片的逆二维傅里叶变换。







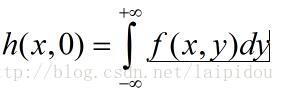
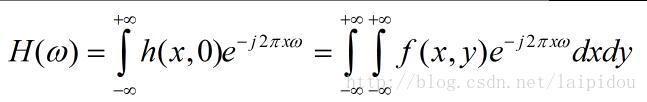
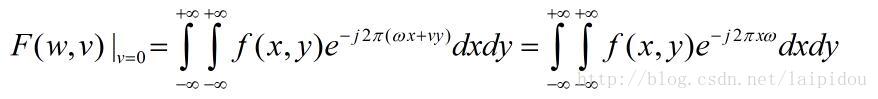
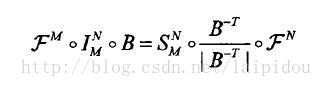
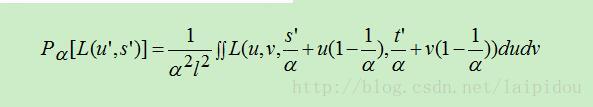
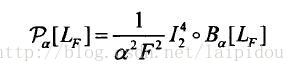













 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








