TOJ 2814

题目连接:

http://acm.tzc.edu.cn/acmhome/problemdetail.do?&method=showdetail&id=2814

题目类型:

数论 - 计算几何

数据结构:

无

思路分析:

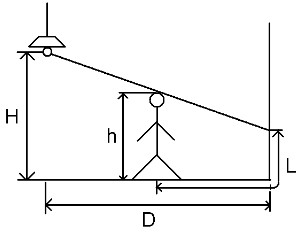
要求的L的最大值

首先需要建立关于L的方程式

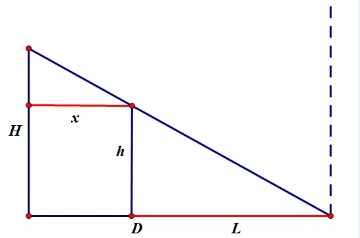
1. 判定当影子全部在地面上的情况,

也就是 x + L <= D

L = h * x / ( H - h )

可知 L 为单调递增函数

所以 x 的值需要尽可能的大

最大达到 x + L = D

也就是 x = ( D * H - h * D ) / H  的时候

这时候 L = h * D / H;

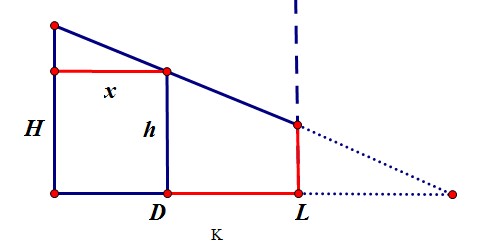
2. 投影出现在墙上的情况

设地和影子虚像的总长为 K

那么 地上未呈现的影子长度为 K - D

地上已呈现的影子长度为 D - x

所以 L 的总长为 地上这部分加上墙上这部分

得 L = ( D - x ) + ( ( H - h ) * ( K - D ) ) / x

    K = H * x / ( H - h )

联立方程 得

L = ( -1 * x * x + ( H + D ) * x + ( h * D - D * H ) ) / x

要求L的最大值 必须点求的 x 的极值点

对L求导

得 L' = -1 + ( -1 ) *  ( h * D - D * H ) / ( x * x ) = 0

     1 = D * ( H - h ) / ( x * x )

     x = sqrt( D * ( H - h ) ) 

所以 x 等于 sqrt( D * ( H - h ) )  时  ( D -  h * D / H <= x <= D )

L取得最大值

比较两种情况的最大值

能得出 最后的答案

证明:

略

源代码:

#include <iostream>
#include <stdio.h>
#include <math.h>

using namespace std;

int main()
{
	int t;
	double H, h, D;
	
	scanf( "%d", &t );
	
	while( t -- )
	{
		scanf( "%lf%lf%lf", &H, &h, &D );
		
		double x = D >= sqrt( D * ( H - h ) ) ? sqrt( D * ( H - h ) ) : D;
		
		if( x < ( D - h * D / H ) )
		{
			x = D - h * D / H;
		}
		
		printf( "%.3lf\n", max( h * D / H, ( - x * x + ( H + D ) * x + D * ( h - H ) ) / x ) );
	}
	
	return 0;
}