图的遍历:深度优先、广度优先
遍历
图的遍历是指从图中的某一顶点出发,按照一定的策略访问图中的每一个顶点。当然,每个顶点有且只能被访问一次。
在图的遍历中,深度优先和广度优先是最常使用的两种遍历方式。这两种遍历方式对无向图和有向图都是适用的,并且都是从指定的顶点开始遍历的。先看下两种遍历方式的遍历规则:
深度优先
深度优先遍历也叫深度优先搜索(Depth First Search)。它的遍历规则:不断地沿着顶点的深度方向遍历。顶点的深度方向是指它的邻接点方向。
具体点,给定一图G=<V,E>,用visited[i]表示顶点i的访问情况,则初始情况下所有的visited[i]都为false。假设从顶点V0开始遍历,则下一个遍历的顶点是V0的第一个邻接点Vi,接着遍历Vi的第一个邻接点Vj,……直到所有的顶点都被访问过。
所谓的第一个是指在某种存储结构中(邻接矩阵、邻接表),所有邻接点中存储位置最近的,通常指的是下标最小的。在遍历的过程中有两种情况经常出现
- 某个顶点的邻接点都已被访问过的情况,此时需回溯已访问过的顶点。
- 图不连通,所有的已访问过的顶点都已回溯完了,仍找不出未被访问的顶点。此时需从下标0开始检测visited[i],找到未被访问的顶点i,从i开始新一轮的深度搜索。
看一个例子
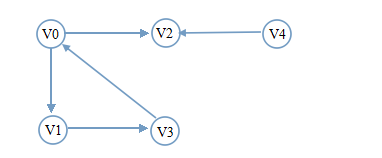
从V
0
开始遍历
遍历分析:V0有两个邻接点V1和V2,选择下标最小的V1遍历。接着从V1开始深度遍历,V1只有邻接点V3,也就是没有选的:遍历V3。接着从V3开始遍历,V3只有邻接点V0,而V0已经被遍历过。此时出现了上面提到的情况一,开始回溯V1,V1无未被遍历的邻接点,接着回溯V0,V0有一个未被遍历的邻接点V2,新的一轮深度遍历从V2开始。V2无邻接点,且无法回溯。此时出现了情况二,检测visited[i],只有V4了。深度遍历完成。看到回溯,应该可以想到需要使用栈。
遍历序列是
V0->V1->V3->V2->V4。
从其它顶点出发的深度优先遍历序列是:
V1->V3->V0->V2->V4。
V2->V0->V1->V3->V4。
V3->V0->V1->V2->V4。
V4->V2->V0->V1->V3。
以上结果,我们稍后用于测试程序。
结合在图的实现:邻接矩阵中的代码,我们看下在邻接矩阵形式下的图的深度遍历算法:
深度优先代码
- /*
- 深度优先搜索
- 从vertex开始遍历,visit是遍历顶点的函数指针
- */
- void Graph::dfs(int vertex, void (*visit)(int))
- {
- stack<int> s;
- //visited[i]用于标记顶点i是否被访问过
- bool *visited = new bool[numV];
- //count用于统计已遍历过的顶点数
- int i, count;
- for (i = 0; i < numV; i++)
- visited[i] = false;
- count = 0;
- while (count < numV)
- {
- visit(vertex);
- visited[vertex] = true;
- s.push(vertex);
- count++;
- if (count == numV)
- break;
- while (visited[vertex])
- {
- for (i = 0; i < numV
- && (visited[i]
- || matrix[vertex][i] == 0 || matrix[vertex][i] == MAXWEIGHT); i++);
- if (i == numV) //当前顶点vertex的所有邻接点都已访问完了
- {
- if (!s.empty())
- {
- s.pop(); //此时vertex正是栈顶,应先出栈
- if (!s.empty())
- {
- vertex = s.top();
- s.pop();
- }
- else //若栈已空,则需从头开始寻找新的、未访问过的顶点
- {
- for (vertex = 0; vertex < numV && visited[vertex]; vertex++);
- }
- }
- else //若栈已空,则需从头开始寻找新的、未访问过的顶点
- {
- for (vertex = 0; vertex < numV && visited[vertex]; vertex++);
- }
- }
- else //找到新的顶点应更新当前访问的顶点vertex
- vertex = i;
- }
- }
- delete[]visited;
- }
广度优先
广度优先遍历也叫广度优先搜索(Breadth First Search)。它的遍历规则:
- 先访问完当前顶点的所有邻接点。(应该看得出广度的意思)
- 先访问顶点的邻接点先于后访问顶点的邻接点被访问。
具体点,给定一图G=<V,E>,用visited[i]表示顶点i的访问情况,则初始情况下所有的visited[i]都为false。假设从顶点V0开始遍历,且顶点V0的邻接点下表从小到大有Vi、Vj...Vk。按规则1,接着应遍历Vi、Vj和Vk。再按规则2,接下来应遍历Vi的所有邻接点,之后是Vj的所有邻接点,...,最后是Vk的所有邻接点。接下来就是递归的过程...
在广度遍历的过程中,会出现图不连通的情况,此时也需按上述情况二来进行:测试visited[i]...。
在上述过程中,可以看出需要用到队列。
举个例子,还是同样一幅图:

从V
0
开始遍历
遍历分析:V0有两个邻接点V1和V2,于是按序遍历V1、V2。V1先于V2被访问,于是V1的邻接点应先于V2的邻接点被访问,那就是接着访问V3。V2无邻接点,只能看V3的邻接点了,而V0已被访问过了。此时需检测visited[i],只有V4了。广度遍历完毕。
遍历序列是
遍历序列是
V0->V1->V2->V3->V4。
从其它顶点出发的广度优先遍历序列是
V1->V3->V0->V
2
->
V
4
。
V2->V0->V1->V3->V4。
V3->V0->V1->V2->V4。
V4->V2->V0->V1->V3。
以上结果,我们同样用于测试程序。
在邻接矩阵下,图的广度遍历算法
广度优先代码
- /*
- 广度优先搜索
- 从vertex开始遍历,visit是遍历顶点的函数指针
- */
- void Graph::bfs(int vertex, void(*visit)(int))
- {
- //使用队列
- queue<int> q;
- //visited[i]用于标记顶点i是否被访问过
- bool *visited = new bool[numV];
- //count用于统计已遍历过的顶点数
- int i, count;
- for (i = 0; i < numV; i++)
- visited[i] = false;
- q.push(vertex);
- visit(vertex);
- visited[vertex] = true;
- count = 1;
- while (count < numV)
- {
- if (!q.empty())
- {
- vertex = q.front();
- q.pop();
- }
- else
- {
- for (vertex = 0; vertex < numV && visited[vertex]; vertex++);
- visit(vertex);
- visited[vertex] = true;
- count++;
- if (count == numV)
- return;
- q.push(vertex);
- }
- //代码走到这里,vertex是已经访问过的顶点
- for (int i = 0; i < numV; i++)
- {
- if (!visited[i] && matrix[vertex][i] > 0 && matrix[vertex][i] < MAXWEIGHT)
- {
- visit(i);
- visited[i] = true;
- count ++;
- if (count == numV)
- return;
- q.push(i);
- }
- }
- }
- delete[]visited;
- }
- void visit(int vertex)
- {
- cout << setw(4) << vertex;
- }
- int main()
- {
- cout << "******图的遍历:深度优先、广度优先***by David***" << endl;
- bool isDirected, isWeighted;
- int numV;
- cout << "建图" << endl;
- cout << "输入顶点数 ";
- cin >> numV;
- cout << "边是否带权值,0(不带) or 1(带) ";
- cin >> isWeighted;
- cout << "是否是有向图,0(无向) or 1(有向) ";
- cin >> isDirected;
- Graph graph(numV, isWeighted, isDirected);
- cout << "这是一个";
- isDirected ? cout << "有向、" : cout << "无向、";
- isWeighted ? cout << "有权图" << endl : cout << "无权图" << endl;
- graph.createGraph();
- cout << "打印邻接矩阵" << endl;
- graph.printAdjacentMatrix();
- cout << endl;
- cout << "深度遍历" << endl;
- for (int i = 0; i < numV; i++)
- {
- graph.dfs(i, visit);
- cout << endl;
- }
- cout << endl;
- cout << "广度遍历" << endl;
- for (int i = 0; i < numV; i++)
- {
- graph.bfs(i, visit);
- cout << endl;
- }
- system("pause");
- return 0;
- }
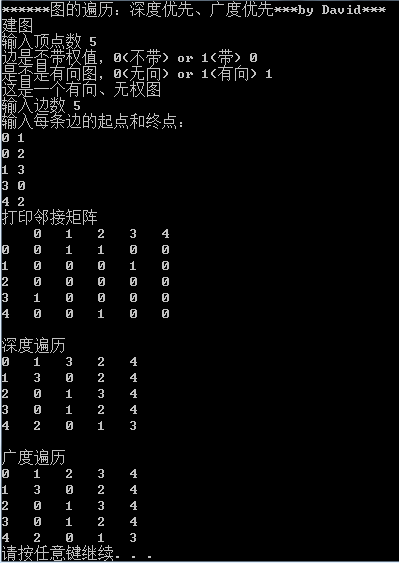
仔细对照测试结果,我们的代码是没有问题的。
完整代码下载:图的遍历:深度优先、广度优先
小结
对于某个图来说,深度优先遍历和广度优先遍历的序列不是唯一的,但当图的存储结构一确定,它的遍历序列就是唯一的。因为当有多个候选点时,我们总是优先选择下标最小的。
深度遍历:其实质是运用了递归思想,在遍历图中时,对图中的每个顶点之多调用一次DNS函数,因为一旦某个顶点把标志成已被访问,就不再从它出发进行搜索了,因此遍历图的实质上是对每个顶点查找其邻接点的过程。
广度遍历:对于图的广度优先遍历的来说,运用了队列的特点,每一个顶点之多进一次队列,遍历图的实质上是通过边或者弧
找邻接点的过程。
从上可以看出,其实广度遍历和深度遍历它们两者的时间复杂度是一样的,两者的不同之处仅仅在于对顶点访问的顺序不同而已。






















 554
554











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








