组合数学 | 图论

图的基本概念

定义：若用点表示研究的对象，用边表示这些对象之间的联系，则图G可以定义为点和边的集合，记作G=(V,E),其中V—点集，E—边集

端点：若有边e可表示为e=vivj，称vi和vj是边e的端点，反之称边e为vi和vj的关联边。若点vi、vj与同一条边关联，称点vi和vj相邻；若边ei和ej具有公共端点，称边ei和ej相邻。

环：如果边e的两个端点相重，称该边为环。如e1

多重边：如果两点之间的边多于一条，称为多重边。如e4和e5

简单图：无环、无多重边的图

有向图：图中的边是有方向的

无向图：图中的边没有方向

次（度）：与某一个点vi相关联的边的数目称为点vi的度，记作d(vi),如d(v1)=4，d(v3)=5，d(v5)=1

奇度点：度为奇数的点，d(v3)=5

偶度点：度为偶数的点，d(v2)=4

悬挂点：度为1的点，d(v5)=1

孤立点：度为0的点

入度：在有向图中，以a为终点的边的条数称为a的入度，记作deg-(a)或d-(a)

出度：在有向图中，以a为始点的边的条数称为a的出度，记作deg+(a)或d+(a)

d-(v1)=3，d-(v2)=0，d(v3)=3，d-(v4)=3

d+(v1)=2，d+(v2)=3，d+(v3)=2，d+(v4)=2

握手定理：设无向图G(V,E)，有n个顶点，m条边，则G中所有顶点的度之和等于m的两倍。即Σd(vi) = 2m

推论：无向图中度为奇数的顶点个数恰有偶数个

定理：设有向图D(V,E)有n个顶点，m条边，则G中所有顶点的入度之和等于所有顶点的出度之和，也等于m。Σd+(vi) = Σd-(vi) = m

例：空间中不可能有这样的多面体存在，他的面数是奇数，而且每个面由奇数条线段组成。

证明：如果有这样的多面体，以此多面体的面集合为顶点集构造一个图G，当且仅当两个面有公共边界时，在相应的两顶点之间连一条边，于是G有奇数个顶点，且每个顶点都为奇点，与定理（度为奇数的顶点个数恰有偶数个）矛盾，故不存在这样的多面体。

特殊的图

完全图

二部图

若能将无向图G=(V,E)的顶点集V划分成两个不相交的非空子集V1和V2，使得G中的任何一条边的两个端点一个属于V1，另一个属于V2，则称G为二部图（或偶图），记作G=(XUY，E)，X,Y称为G的一个划分（二分类）

完全二部图

在简单二部图G(XUY，E)中，若X的每个顶点与Y的每个顶点有边连接，则称G为完全二部图；若|X|=m,|Y|=n,则记此完全二部图为Km,n。特别地，K1,n称为星

1. 

   路、圈、连通
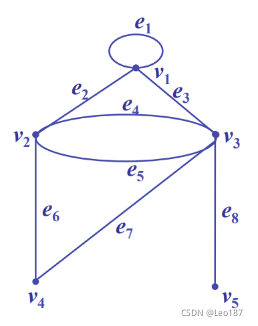
   1. 途径：图G中一个顶点和边交替出现的有限非空序列 v1e2v2e4v3e7v4e7v3e5v2 e6v4
   2. 迹：各边相异的途径  v1 e2 v2 e4 v3 e7v4 e6 v2 e5v3 e8 v5
   3. 路：各顶点相异的迹 v1 e2 v2 e4 v3 e7v4
   4. 闭途径：具有正的长且起点和终点相同的途径 v1e2v2e4v3e7v4e7v3e5v2e6v4e7v3e3v1
   5. 闭迹：也称回路  v2 e4 v3 e7v4 e6 v2 e5 v3 e3 v1 e2 v2
   6. 圈：起点和终点相同的路 有n个顶点的一个圈记作Cn  v1 e2 v2 e6 v4 e7 v3 e3 v1
   7. 连通图：图G中任二顶点都连通
   8. 图的分支：若图G的顶点集V(G)可划分为若干个非空子集V1,V2,V3…，使得两顶点属于同一子集当且仅当他们在G中连通，则称每个子图G(Vi)为图G的一个分支(i=1,2,3…)
   9. 欧拉回路G=(V,E)，称包含E中所有边的回路为欧拉回路

欧拉定理：无向图存在欧拉回路的充要条件是：a.图是连通的，b.图中奇次顶点个数是0个

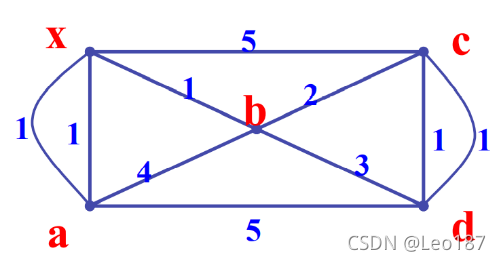
       中国邮政问题：一个邮递员从邮局出发，然后再返回邮局，如果他必须走过他所管辖的每条街至少一次，问如何选择路线可使路程最短？

       解：如果G中全部顶点都为偶度点，则Euler闭迹存在，若是奇度点，则奇度点的个数必为偶数，于是可组成奇度点对，在其间增加重边，使重边的权等于原来边的权，可使G中全部顶点变为偶度点，这时Euler闭迹存在

x-a-b-x-a-d-b-c-d-c-x  总里程24

平面图

定义：G(V,E)是一个无向图，如果能够把G的所有结点和边画在平面上，且使得任何两条边除了端点外没有其他的交点

任何一个包含非平面图作为部分结构的图也都是非平面图

设G=(V,E)是平面图，当且仅当G不含有K5和K3,3或他们的划分作为子图

面：设图G=(V,E)是一个连通平面图，图中各边界定的区域称为平面图的面

边界：界定面的闭的路径称为边界

度(次数)：面r的边界长度称为面r的度，记作deg(r)，又称为r的次数

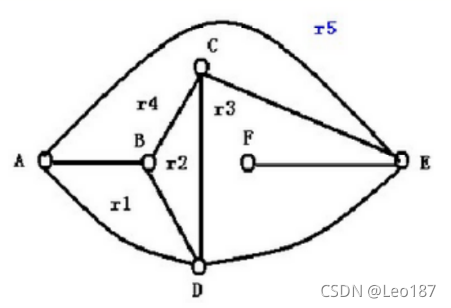
deg(r1)=3  deg(r2)=3  deg(r3)=5  deg(r4)=4  deg(r5)=3

deg(r1)+ deg(r2)+deg(r3)+ deg(r4)+ deg(r5)=18

定理：有限平面图中，面的次数(度)之和等于其边数的两倍。

欧拉定理：设G为平面连通图，v为顶点数，e为边数，r为面数，那么欧拉公式成立  v-e+r=2

例：已知一个平面图中结点数v=10，每个面均由4条边围成，求该平面图的边数和面数。

解：因每个面的次数均为4，则4r=2e，即2r=e,又v=10，代入欧拉公式v-e+r=2,有10-2r+r=2，解得r=8，e=2r=16

树形图与最小支撑树

1. 

   树：无圈的连通图

性质：(1).任何树上必存在次为1的点。(2).n个顶点的树必有n-1条边。(3).树中任意两个顶点之间，恰有且仅有一条链。(4).树连通，但去掉任一条边，必变为不连通。(5).树无回圈，但不相邻的两个点之间加一条边，恰得到一个圈

支撑树

一个图H的每个顶点和每条边都在图G中，则H是G的一个子图。如果H的顶点和G的顶点一样，则H是G的支撑子图。如果H是G的支撑子图，且是树形图，则H是G的支撑树。

子图+顶点相同=支撑子图 

---

转自人民大学张同学笔记