本博客所有内容均整理自《算法图解》,欢迎讨论交流~
相信稍微做过一点学术研究的都不会对“NP完全问题”这个概念感到陌生。它是千禧难题之首。
对于NP完全问题的定义,百度百科是这样给出的:NP完全问题(NP-C问题),是世界七大数学难题之一。 NP的英文全称是Non-deterministic Polynomial的问题,即多项式复杂程度的非确定性问题。简单的写法是 NP=P?,问题就在这个问号上,到底是NP等于P,还是NP不等于P。
通俗地来说,有些计算问题是确定性的,比如加减乘除之类,你只要按照公式推导,按部就班一步步来,就可以得到结果。但是,有些问题是无法按部就班直接地计算出来的。一般这种无法按部就班计算出来的问题,只能通过穷举法等暴力的方法来解决。
1、旅行商问题
对于NP完全问题,有一个经典的例子,就是旅行商问题。
假如你是一个旅行商,需要前往5个不同的城市,当然,你希望找出前往这5个城市的最短路径。为此,你必须计算每条可能的路径,然后一一对比。
那么这里就不得不考虑一个问题了,前往5个城市,可能的路径有多少条呢?
为了解决这个问题,我们先来考虑只有两个城市的情形,然后依次增加城市数量。
2个城市:
对于两个城市,可供选择的路径有两条,如下图所示:
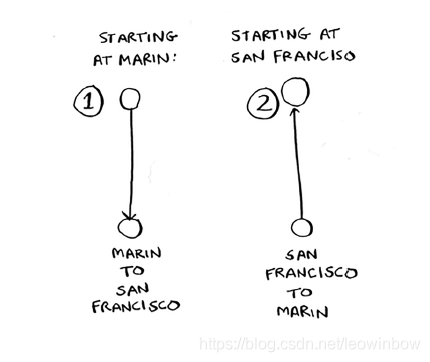
这里可能会有一点争议,那就是理论上来说,从A到B和从B到A应该是相同的,但是实际生活中经常会遇到单行道,所以我们在这里认为从A到B和从B到A不同。
于是,涉及两个城市时,可能的路线有两条。
3个城市:
现在增加一个城市,我们考虑有3个城市的情况。
此时,我们需要首先考虑从哪一个城市出发,有3种情况,而从每个城市出发时,都有两条不同的路线,所以总共有6条路线:
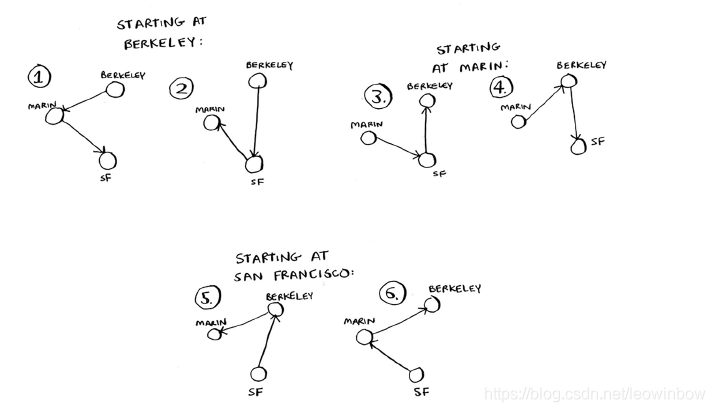
4个城市:
接下来是4个城市的情况。
我们依然是首先考虑从哪个城市出发,于是有4种情况,而选定了出发城市之后,便剩下3个城市,这3个城市的可能路径为6条,所以在选定出发城市的情况下,又分别有6条不同的路径,所以总路径数为4*6=24条。
这里就不详细画出来了。
其实这个问题不难看出来是一个数字阶乘的问题,即涉及n个城市时,可能的路径条数为n!条。
所以前面我们提出的问题就可以有解了,即5个城市时,可能的路线有5!=1*2*3*4*5=120条!
于是,为了寻找这5个城市的最优路线,我们需要遍历120种可能路线,然后一一对比来获取最优路线!
如果你认为这并不是一个多么困难的事情,那么试想一下如果是10个城市呢?10!=3628800。也就是说,你需要计算的可能路线超过300万条。很明显,这很难。
旅行商问题总结一下就是:你需要计算所有的解,并从中选出最小/最短的那一个。为此你必须遍历所有可能,然后一一比对。
旅行商问题就是一个很经典的NP完全问题。
2、集合覆盖问题
还有一种很典型的NP完全问题称为集合覆盖问题。
假设你正在为一个虚构的橄榄球队挑选队员,报名的球员名单如下图所示:
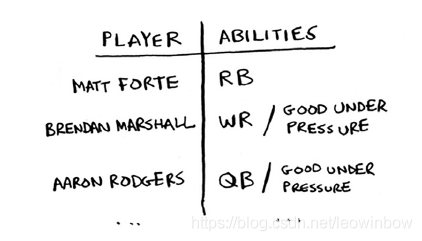
该名单无非就是各个报名选手具备的各种橄榄球技巧。
当然,为了组成一支有实力的球队,我们不可能光挑选一个方面的球员,自然是要挑选各个方面的优秀球员,而且由于名额有限,我们必须在已有的资源中选择一个最优的球员组合。
于是,我们需要列出一个需要的橄榄球技巧清单:优秀的四分卫,优秀的跑卫,擅长雨中作战,能承受压力,等等等等。
在现有的报名选手中,我们根据上面列出的技巧清单来寻找一个最优的球员组合。
面对这个问题,我们可以使用贪婪算法来解决:
- 找出符合最多要求的报名选手。
- 不断重复这个过程,直到球队满足要求或者球队名额已满。
很明显,这是一个集合覆盖问题,根据上面的报名清单我们可以获得以下的集合:
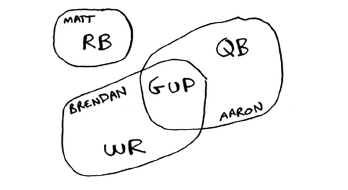
这是只有几个人的情况,如果报名人数多了,这个集合覆盖问题会非常复杂。我们必须一次次找出覆盖面积(或覆盖关键词)最多的集合,直到满足条件。
集合覆盖问题也是一个很典型的NP完全问题。
3、如何识别NP完全问题
既然NP完全问题是多项式复杂程度的非确定性问题,简言之就是难解决的问题,自然也是难判别的。
其实,根本没有一个定理来判断一个问题是否是NP完全问题。只是,还是有很多线索可以帮助我们来做识别的。这些线索罗列如下:
- 元素较少时算法的运行速度非常快,但随着元素数目的增加,速度会变得非常慢。
- 涉及“所有组合”的问题通常是NP完全问题。
- 不能采用分治法的思想将大问题分解成小问题,必须考虑各种可能情况,这很可能是NP完全问题。
- 如果问题涉及“序列”或“集合”,并难以解决,很可能就是NP完全问题。
- 如果问题可转换为旅行商问题或集合覆盖问题,那就肯定是NP完全问题。























 5038
5038











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








