Logistic 逻辑回归原理

Logistic 逻辑回归原理

线性回归

通过历史数据拟合出一条直线，用这条直线对新的数据进行预算。

首先是线性回归：

对于最基本的线性回归问题，公式如下：

                                              

其中x是自变量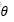， 是权重参数，也就是我们需要去梯度上升求解的具体数值。

Sigmoid函数（将所有的取值映射到[0,1]之间，）：

将两个公式合并：

Sigmoid函数的图形：

因为这里要做的内容是判断属于哪一种类型，但是线性回归预测出来的结果只能是一个实数，我们希望能够通过一个函数来实现最终预测值实现0/1的转换，所以这里就使用Sigmoid函数将 的数值映射到（0,1）之间。然后去求解代价函数，使代价最小，实现预测的分类。

代价函数

这时第一个想到的肯定是线性回归中的方法，利用误差平方代价函数：

但是我们将我们的sigmoid函数代入的话，我们发现这是一个非凸函数，这就意味着他会有很多的局部最小值，不利于我们最终的求解。

所以我们换一种思路来解决：

我们已知样本x和参数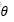 的情况下，正样本和负样本的条件概率，