定义:约数只有1和本身的整数称为质数,或称素数。
计算机或者相关专业,基本上大一新生开始学编程都会接触的一个问题就是判断质数,下面分享几个判断方法,从普通到高效。
1)直观判断法
最直观的方法,根据定义,因为质数除了1和本身之外没有其他约数,所以判断n是否为质数,根据定义直接判断从2到n-1是否存在n的约数即可。C++代码如下:
bool isPrime_1( int num )
{
int tmp =num- 1;
for(int i= 2;i <=tmp; i++)
if(num %i== 0)
return 0 ;
return 1 ;
} 2)直观判断法改进
上述判断方法,明显存在效率极低的问题。对于每个数n,其实并不需要从2判断到n-1,我们知道,一个数若可以进行因数分解,那么分解时得到的两个数一定是一个小于等于sqrt(n),一个大于等于sqrt(n),据此,上述代码中并不需要遍历到n-1,遍历到sqrt(n)即可,因为若sqrt(n)左侧找不到约数,那么右侧也一定找不到约数。C++代码如下:
bool isPrime_2( int num )
{
int tmp =sqrt( num);
for(int i= 2;i <=tmp; i++)
if(num %i== 0)
return 0 ;
return 1 ;
} 3)另一种方法
方法(2)应该是最常见的判断算法了,时间复杂度O(sqrt(n)),速度上比方法(1)的O(n)快得多。最近在网上偶然看到另一种更高效的方法,暂且称为方法(3)吧,由于找不到原始的出处,这里就不贴出链接了,如果有原创者看到,烦请联系我,必定补上版权引用。下面讲一下这种更快速的判断方法;
首先看一个关于质数分布的规律:大于等于5的质数一定和6的倍数相邻。例如5和7,11和13,17和19等等;
证明:令x≥1,将大于等于5的自然数表示如下:
······ 6x-1,6x,6x+1,6x+2,6x+3,6x+4,6x+5,6(x+1),6(x+1)+1 ······
可以看到,不在6的倍数两侧,即6x两侧的数为6x+2,6x+3,6x+4,由于2(3x+1),3(2x+1),2(3x+2),所以它们一定不是素数,再除去6x本身,显然,素数要出现只可能出现在6x的相邻两侧。这里有个题外话,关于孪生素数,有兴趣的道友可以再另行了解一下,由于与我们主题无关,暂且跳过。这里要注意的一点是,在6的倍数相邻两侧并不是一定就是质数。
根据以上规律,判断质数可以6个为单元快进,即将方法(2)循环中i++步长加大为6,加快判断速度,代码如下:
bool isPrime_3( int num )
{
//两个较小数另外处理
if(num ==2|| num==3 )
return 1 ;
//不在6的倍数两侧的一定不是质数
if(num %6!= 1&&num %6!= 5)
return 0 ;
int tmp =sqrt( num);
//在6的倍数两侧的也可能不是质数
for(int i= 5;i <=tmp; i+=6 )
if(num %i== 0||num %(i+ 2)==0 )
return 0 ;
//排除所有,剩余的是质数
return 1 ;
} 算法性能测试:
编写测试代码,使用较多数据测试比较几种方法的判断效率,数据量40w,代码如下:
#include <iostream>
#include <string>
#include <ctime>
#include <vector>
using namespace std;
bool isPrime_1( int num );
bool isPrime_2( int num );
bool isPrime_3( int num );
int main()
{
int test_num =400000;
int tstart ,tstop; //分别记录起始和结束时间
//测试第一个判断质数函数
tstart=clock ();
for(int i= 1;i <=test_num; i++)
isPrime_1(i );
tstop=clock ();
cout<<"方法(1)时间(ms):" <<tstop- tstart<<endl ;//ms为单位
//测试第二个判断质数函数
tstart=clock ();
for(int i= 1;i <=test_num; i++)
isPrime_2(i );
tstop=clock ();
cout<<"方法(2)时间(ms):" <<tstop- tstart<<endl ;
//测试第三个判断质数函数
tstart=clock ();
for(int i= 1;i <=test_num; i++)
isPrime_3(i );
tstop=clock ();
cout<<"方法(3)时间(ms):" <<tstop- tstart<<endl ;
cout<<endl ;
system("pause" );
return 0 ;
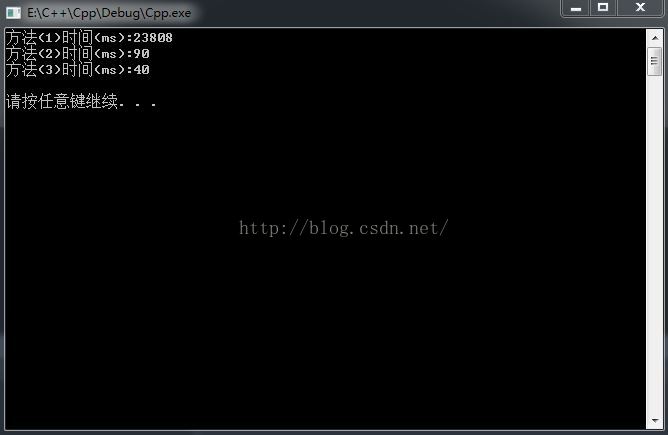
} 运行结果如下;
可以看出,判断到40w,效率上方法(1)明显要差得多,方法(2)和方法(3)在这种测试数量下时间相差2倍多
单独对比方法(2)和(3),数据量加到1000w,结果如下:
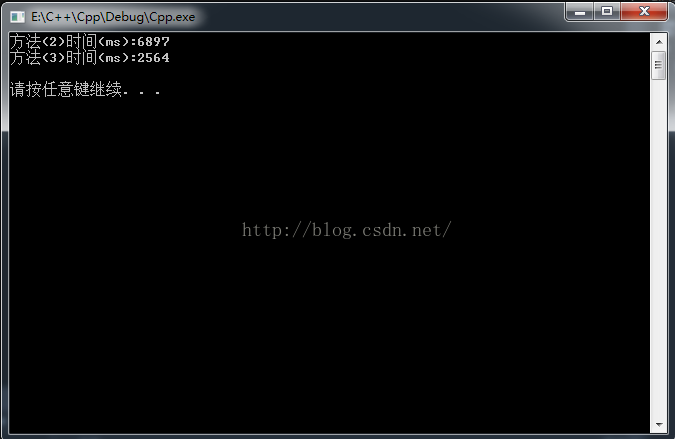
可以看出,方法(2)和方法(3)在这种测试数量下时间相差依然是2倍多,不过已经是很不错的提升。
对了,附上运行环境,CPU-i5-3210,内存4G,win7,vs2012。
好了,判断质数的方法暂时就到这里,不足之处欢迎各道友指出。、
转载自http://blog.csdn.net/huang_miao_xin/article/details/51331710
向大佬比心~~~






















 708
708











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








