误差反向传播法( )
)
对神经网络模型而言,梯度下降法需要计算损失函数对参数的偏导数,如果用链式法则对每个参数逐一求偏导,这是一个非常艰巨的任务!这是因为:
- 模型参数非常多——现在的神经网络中经常会有上亿个参数,而这里每求一个分量的偏导都要把所有参数值代入损失函数求两次损失函数值,而且每个分量都要执行这样的计算。相当于每计算一次梯度需要2x1亿x1亿次计算,而梯度下降算法又要求我们多次(可能是上万次)计算梯度
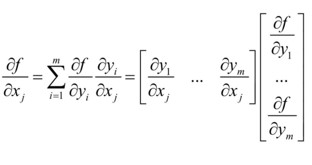
- 复合函数非常复杂——数值计算偏导涉及到矩阵微分,效率比较低。这样巨大的计算量即使是超级计算机也很难承受(前世界第一的“神威·太湖之光”超级计算机峰值性能为12.5亿亿次/秒,每秒也只能计算大概6次梯度)

反向传播算法(back propagation,简称BP模型)是1986年由Rumelhart和McClelland为首的科学家提出的概念,是用于多层神经网络训练的著名算法,有理论依据坚实、推导过程严谨、概念清楚、通用性强等优点。
学习误差反向传播法有两种方式:一是基于计算式,这种方法严密且简洁,但是对数学功底要求比较高;二是基于计算图(Computational graph),比较直观,易于理解。目前各大深度学习框架如Tensorflow、PyTorch、Theano等都以计算图作为描述反向传播算法的基础。本章我们将基于计算图来介绍误差反向传播法。
计算图
计算图将计算过程用图形来表示。这里说的图形是数据结构图,通过多个节点和边表示(连接节点的直线称为“边”)。下面用一个实例来说明:
例,超市里苹果每个100日元,消费税是 10%。如果买 2 个苹果,请计算支付金额。
计算图如下
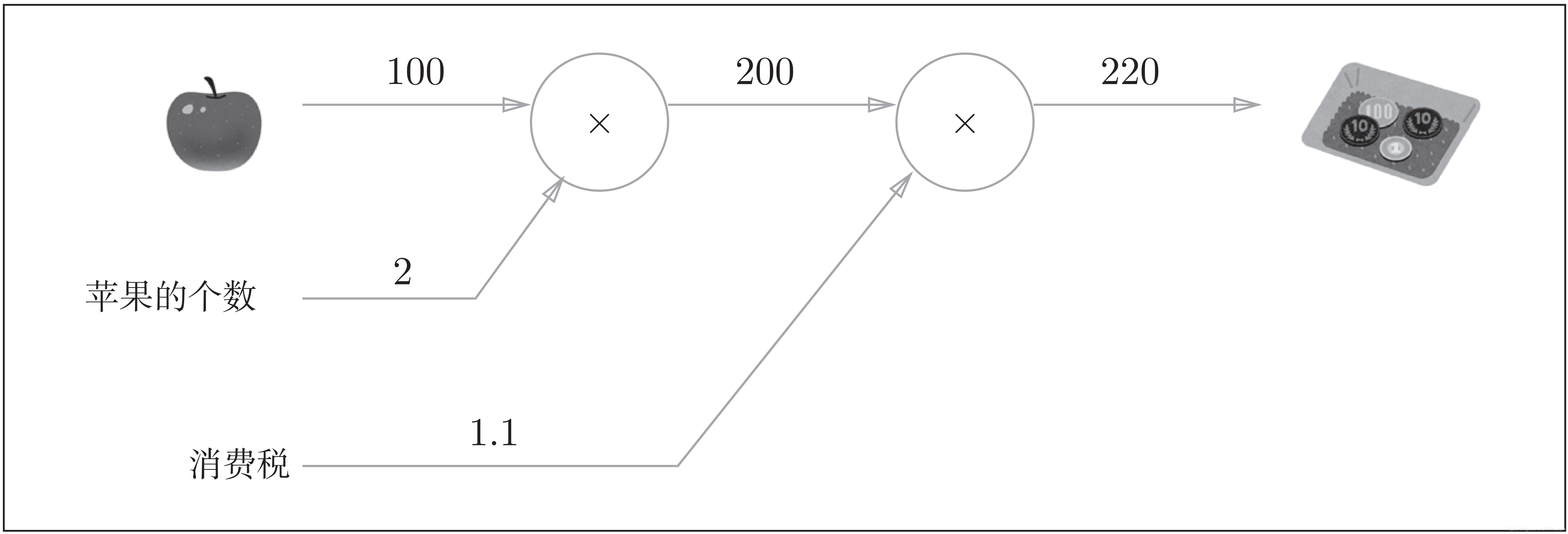
如上图所示,开始时,苹果的单价100日元和苹果的个数2一起流到“×”节点,变成200日元,然后被传递给下一个节点。接着,这个200日元和消费税1.1一起流向第二个“×”节点,变成220日元。因此,从这个计算图的结果可知,答案为220日元。
用计算图解题的情况下,需要按如下流程进行:
- 构建计算图
- 在计算图上,从左向右进行计算
这里的第 2 歩“从左向右进行计算”是一种正方向上的传播,简称为正向传播(forward propagation)。正向传播是从计算图出发点到结束点的传播。考虑反向(从图上看的话,就是从右向左)的传播。实际上,这种传播称为反向传播(backward propagation)。反向传播将在接下来的导数计算中发挥重要作用。
假设我们想知道苹果价格的上涨会在多大程度上影响最终的支付金额,即求“支付金额关于苹果的价格的导数”。设苹果的价格为 ,支付金额为
,则相当于求
。这个导数的值表示当苹果的价格稍微上涨时,支付金额会增加多少。
“支付金额关于苹果的价格的导数”的值可以通过计算图的反向传播求出来。结果如下图所示:
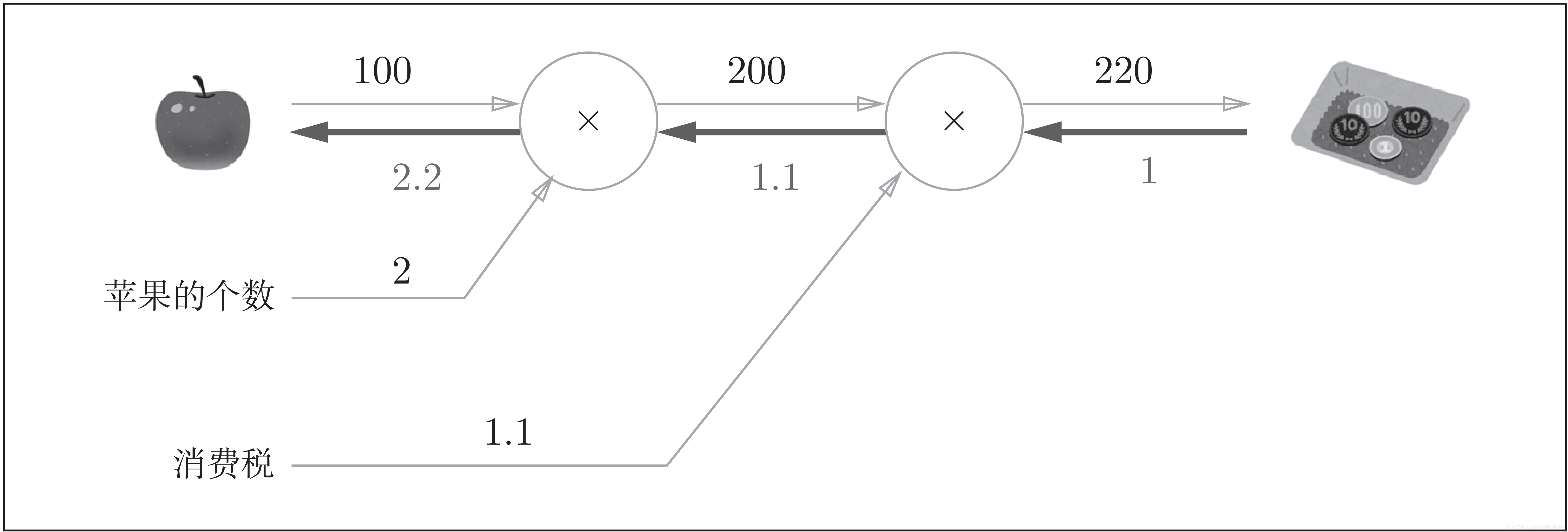
如图所示,反向传播使用与正方向相反的箭头(粗线)表示。反向传播传递“局部导数”,将导数的值写在箭头的下方。在这个例子中,反向传播从右向左传递导数的值(1 → 1.1 → 2.2)。从这个结果中可知,“支付金额关于苹果的价格的导数”的值是2.2。这意味着,如果苹果的价格上涨1日元,最终的支付金额会增加2.2日元(严格地讲,如果苹果的价格增加某个微小值,则最终的支付金额将增加那个微小值的2.2倍)。
这里只求了关于苹果的价格的导数,不过“支付金额关于消费税的导数”、“支付金额关于苹果的个数的导数”等也都可以用同样的方式算出来。并且,计算中途求得的导数的结果(中间传递的导数)可以被共享,从而可以高效地计算多个导数。
综上,计算图的优点是,可以通过正向传播和反向传播高效地计算各个变量的导数值。
计算图的反向传播
假设存在 的计算,这个计算的反向传播如下图所示:

如图所示,反向传播的计算顺序是,将信号 乘以节点的局部导数
,然后将结果传递给下一个节点。
这里所说的局部导数是指正向传播中函数 的导数,也就是
关于
的导数
。
比如,假设 , 则局部导数为
。把这个局部导数乘以上游传过来的值(本例中为
),然后传递给前面的节点。
这就是反向传播的计算顺序。通过这样的计算,可以高效地求出导数的值,这是反向传播的要点。
复合函数求导的链式法则和计算图
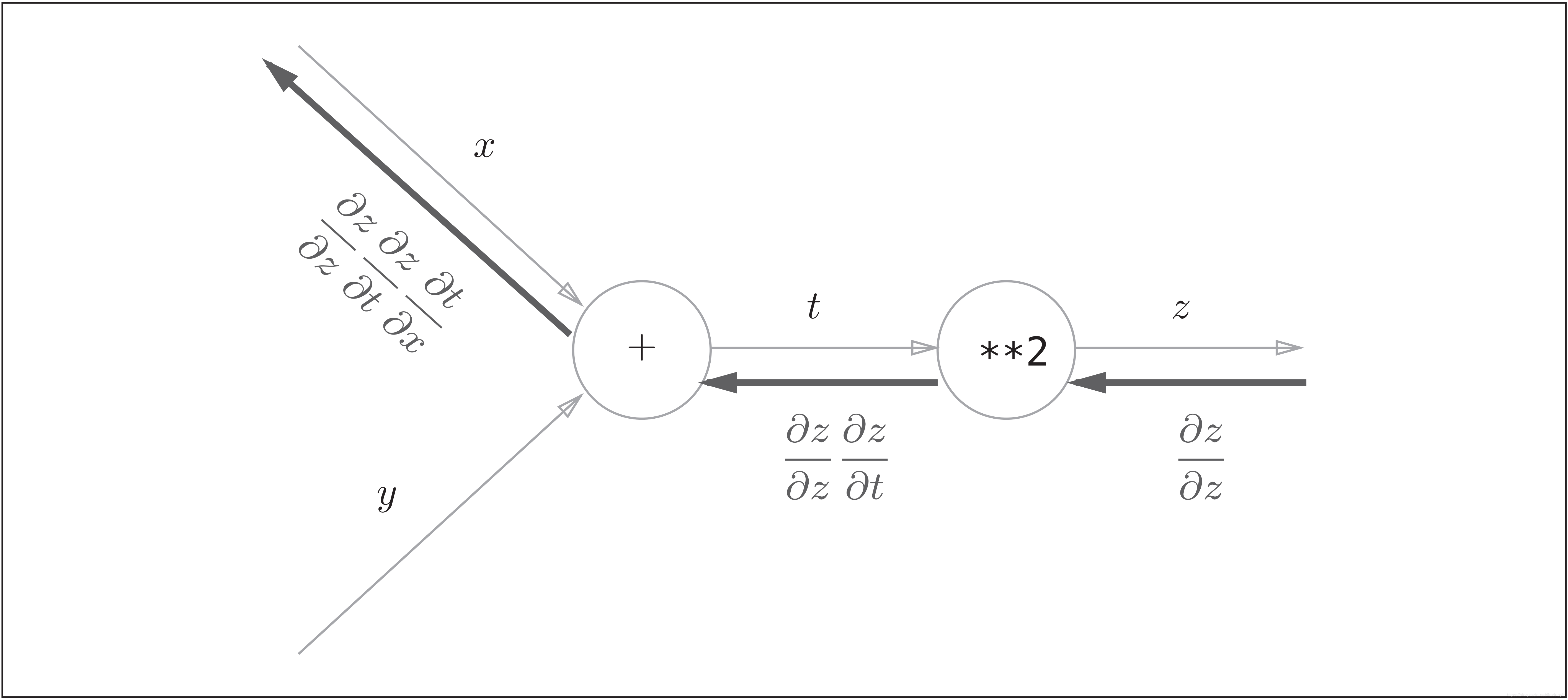
如图所示,计算图的反向传播从右到左传播信号。反向传播的计算顺序是,先将节点的输入信号乘以节点的局部导数(偏导数),然后再传递给下一个节点。比如,反向传播时,“**2”节点的输入是 ,将其乘以局部导数
(因为正向传播时输入是
、输出是
,所以这个节点的局部导数是
),然后传递给下一个节点。另外,图中反向传播最开始的信号
在前面的数学式中没有出现,这是因为
,所以在刚才的式子中被省略了。
图中需要注意的是最左边的反向传播的结果。根据链式法则
,成立,对应“
关于
的导数”。也就是说,反向传播是基于链式法则的。
各种节点的反向传播
- 加法节点
- 乘法节点
- ReLU层
- Sigmoid层
- 除法节点
- exp节点
- Softmax-with-Loss层
加法节点的反向传播
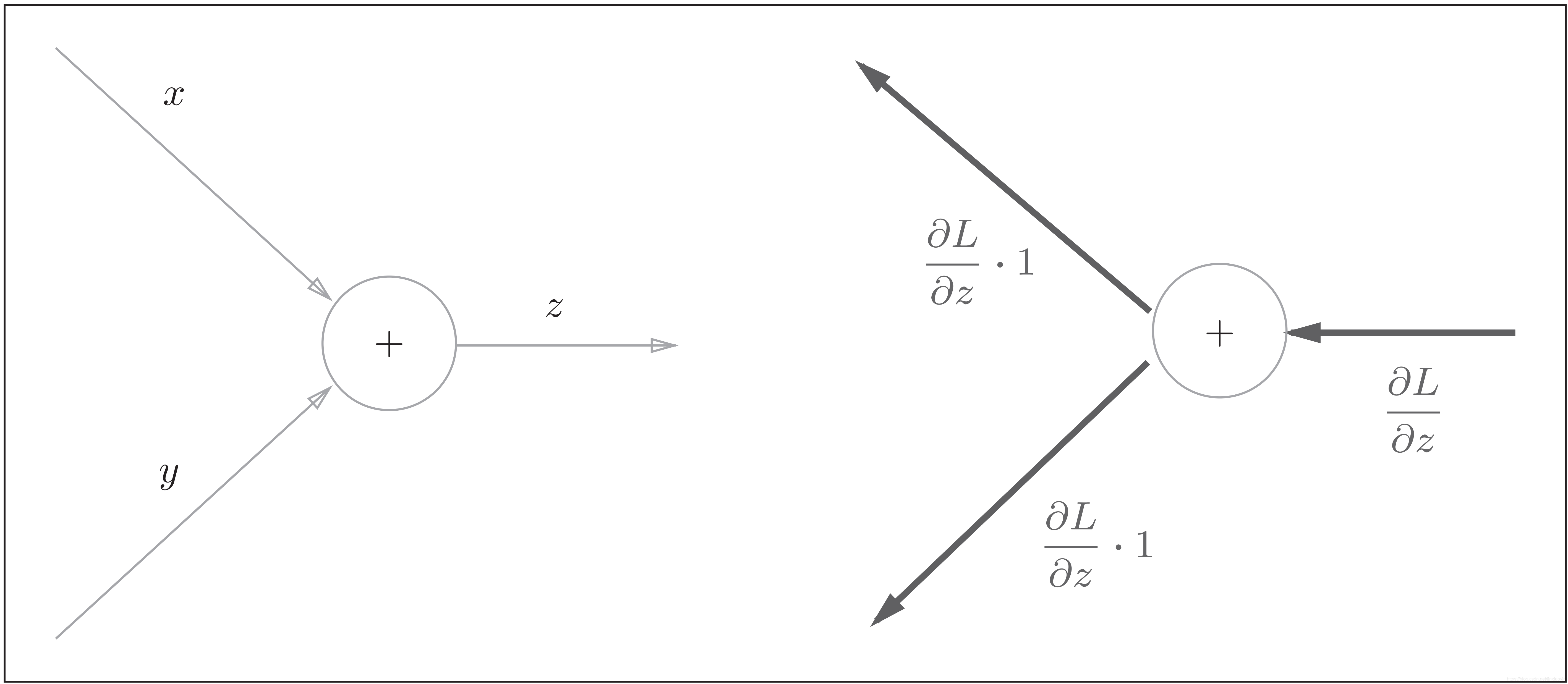
加法节点的反向传播:左图是正向传播,右图是反向传播。如右图的反向传播所示,加法节点的反向传播将上游的值原封不动地输出到下游
乘法节点的反向传播
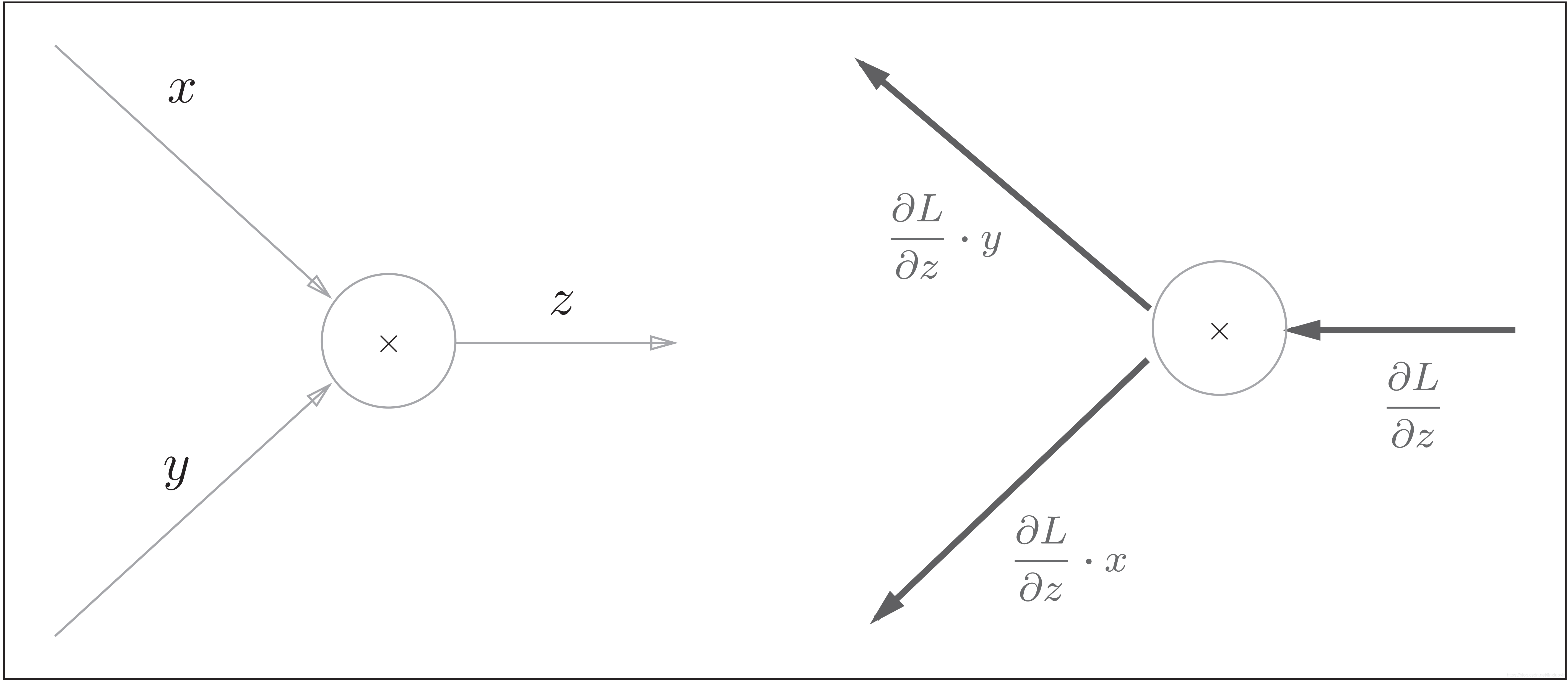
乘法的反向传播:左图是正向传播,右图是反向传播。乘法的反向传播会将上游的值乘以正向传播时的输入信号的“翻转值”后传递给下游。
小测试
在方框中填入数字,完成反向传播
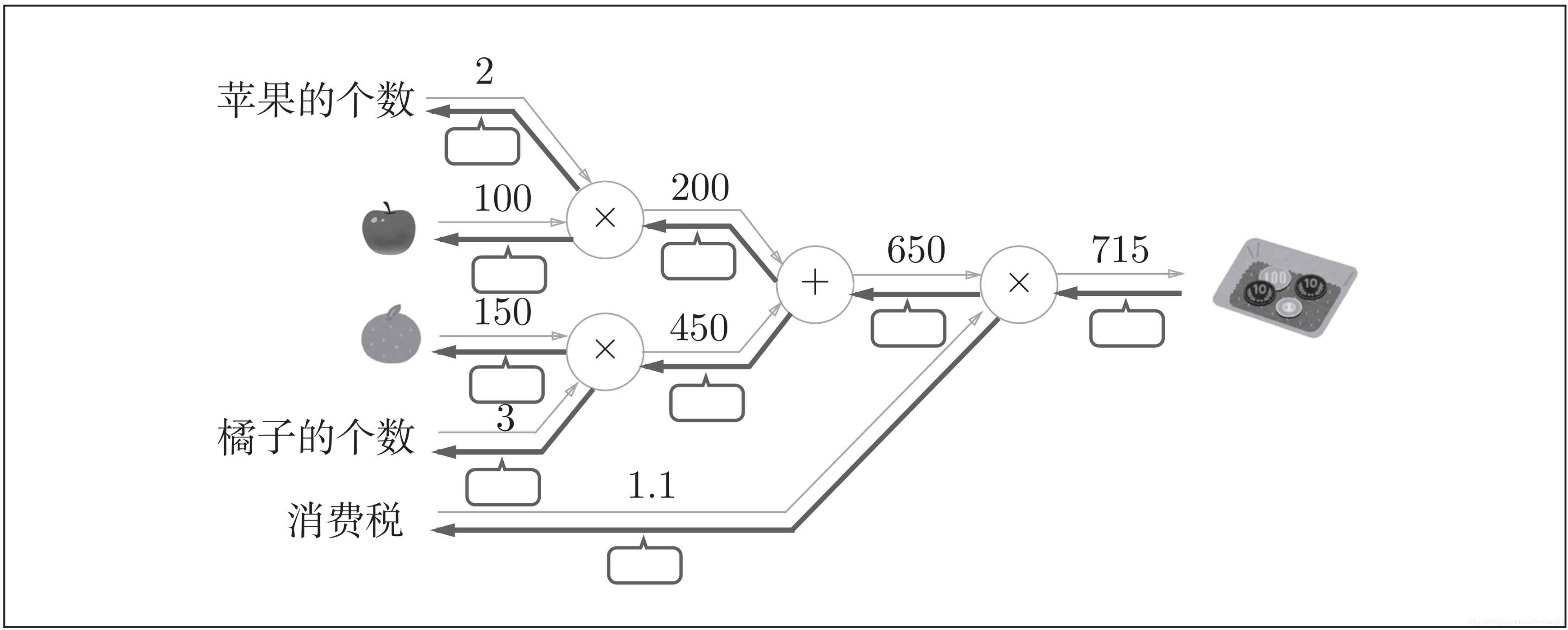
答案见下一章。
ReLU层的反向传播
激活函数ReLU(Rectified Linear Unit)由下式表示:
,
其图形为:
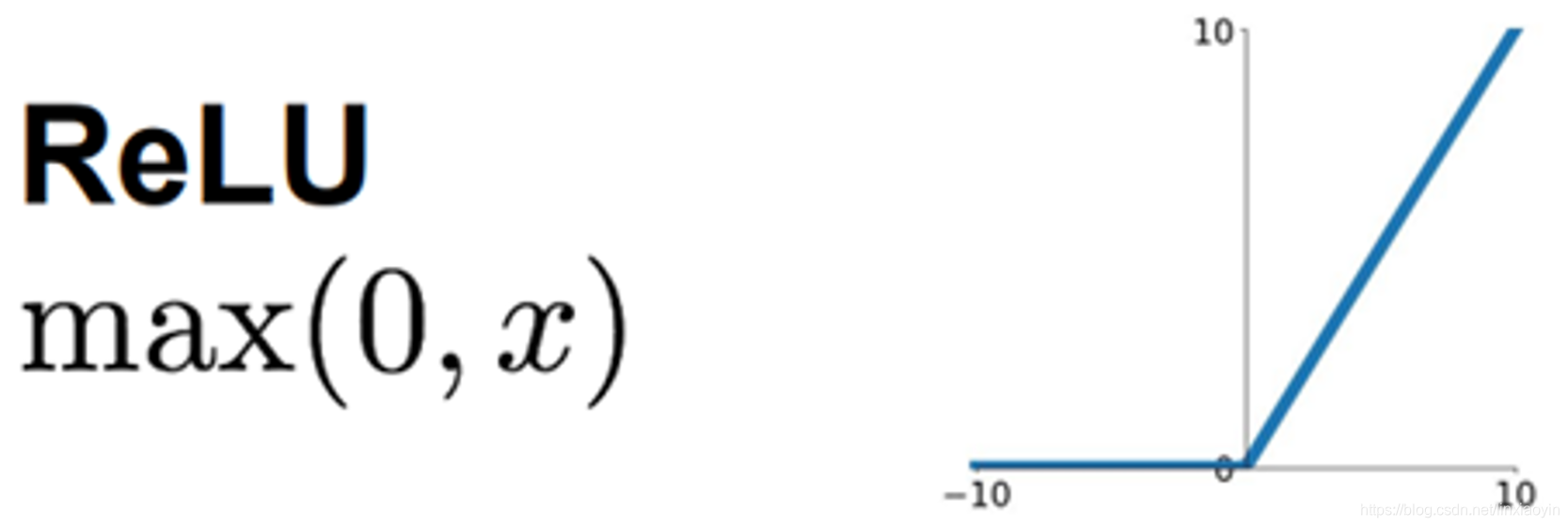
关于
的导数很简单,为:
ReLU函数的计算图:
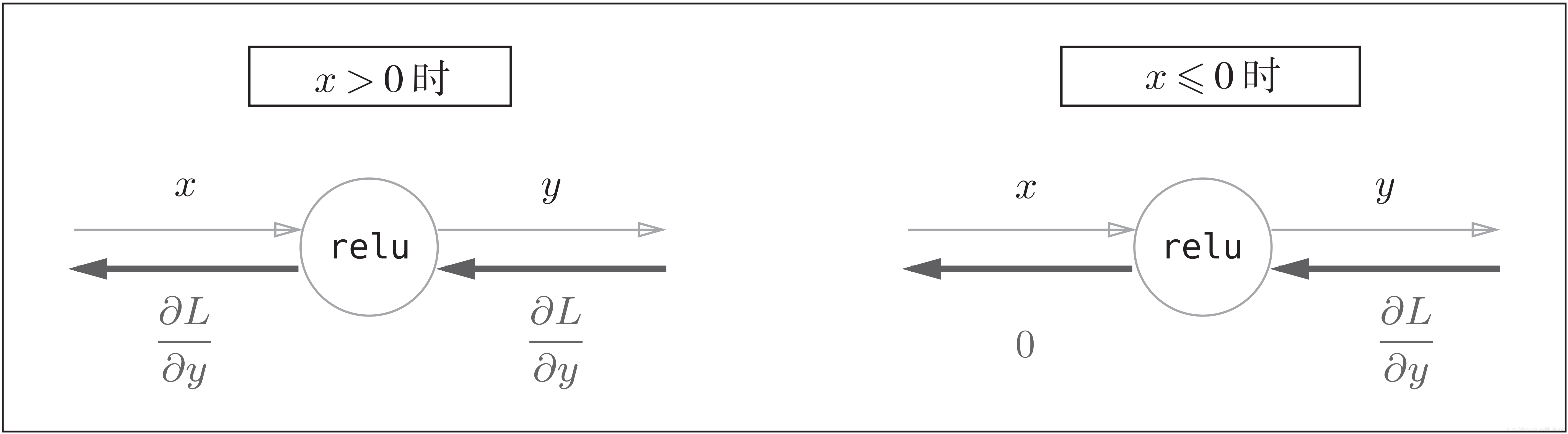
ReLU 层的作用就像电路中的开关一样。正向传播时,有电流通过的话,就将开关设为ON;没有电流通过的话,就将开关设为OFF。反向传播时,开关为ON的话,电流会直接通过;开关为OFF的话,则不会有电流通过。
Sigmoid层的反向传播
我们曾经在第六章《激活函数》中介绍过Sigmoid函数。

Sigmoid函数的正向计算图如下:
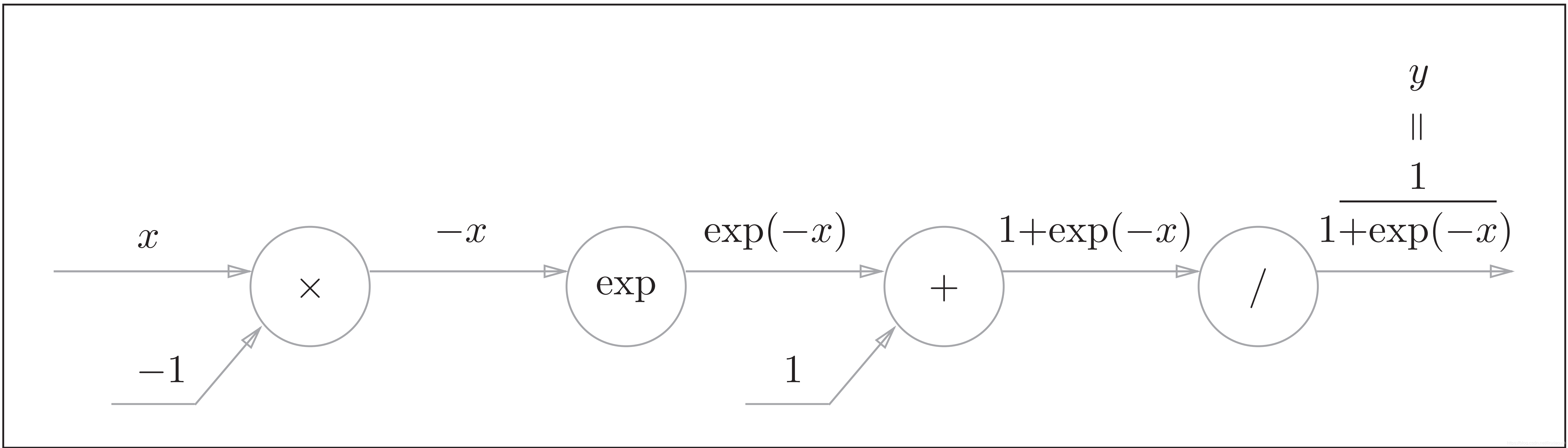
图中除了“×”和“+”节点外,还出现了新的“exp”和“/”节点。
“/”节点会进行 的计算,它的导数为:
反向传播时,会将上游的值乘以 后,再传给下游。计算图如下所示
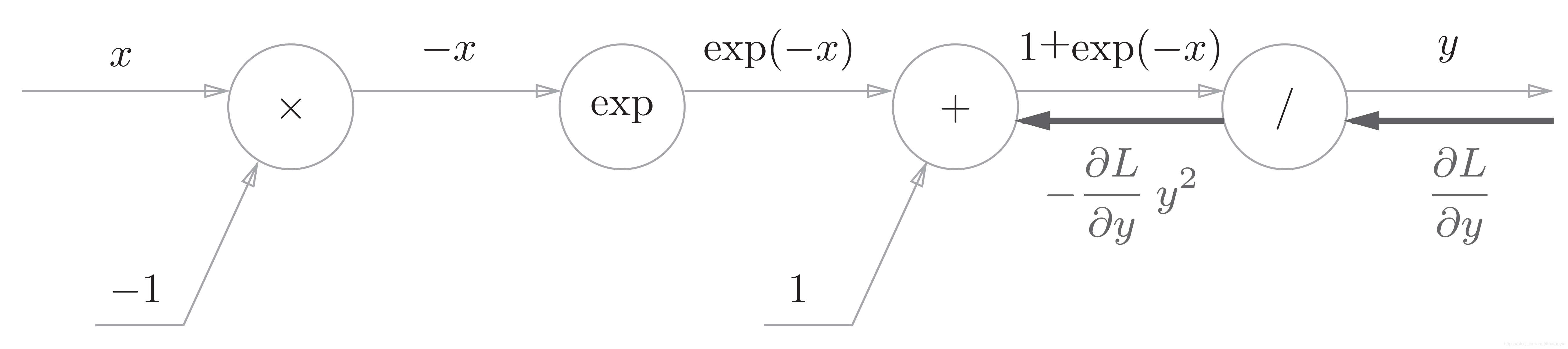
“+”节点将上游的值原封不动地传给下游。计算图如下所示
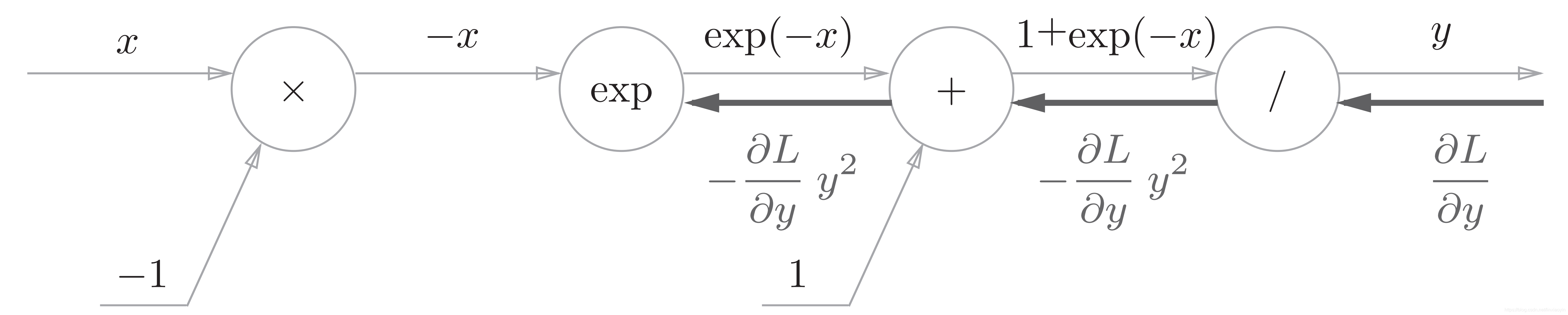
“exp”节点会进行y = exp(x)的计算,它的导数为:
计算图中,上游的值乘以正向传播时的输出(这个例子中是exp(-x))后,再传给下游。
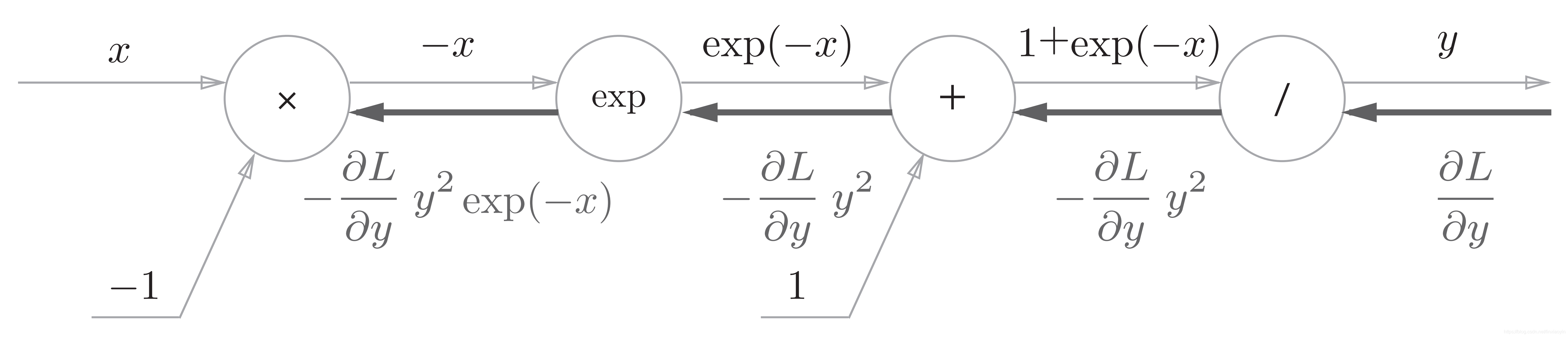
“×”节点将正向传播时的值翻转后做乘法运算。因此,这里要乘以-1
所以Sigmoid函数的完整计算图为:
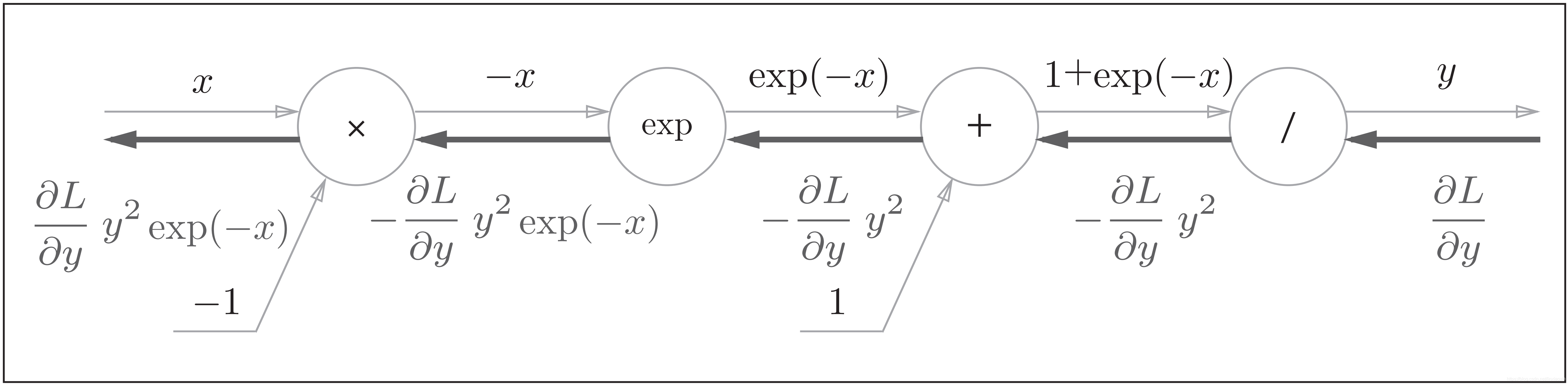
Sigmoid函数的计算图的简洁版为:
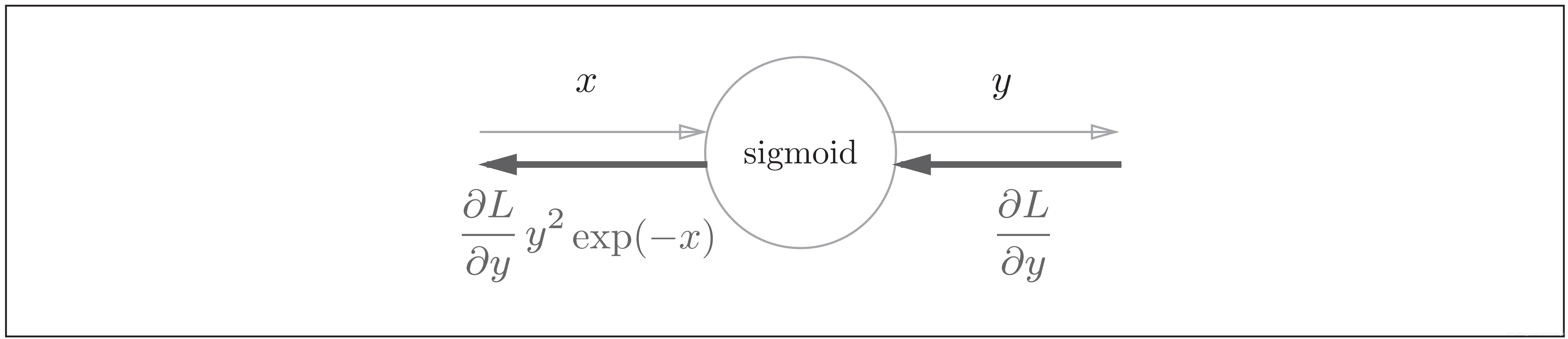

因此,Sigmoid函数的反向传播,只根据正向传播的输出就能计算出来
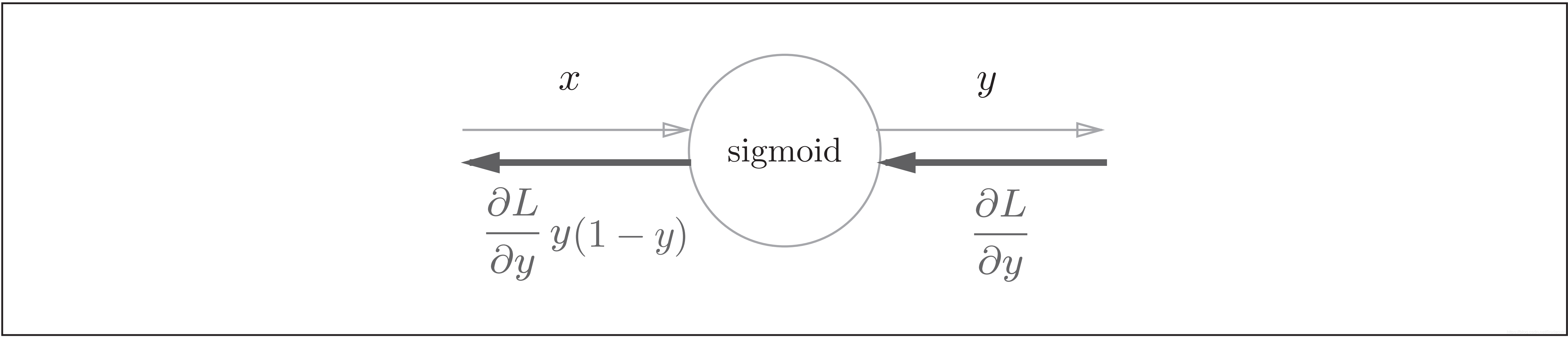
我们在第六章《激活函数》中提到过:
Sigmoid函数被选为激活函数还有一个很重要的原因是它的导数很容易计算:
这里就是对这句话的解释。
Softmax-with-Loss层的反向传播
在这里我们考虑包含交叉熵损失函数,所以称为“Softmax-with-Loss层”。
这里假设要进行3类分类,从前面的层接收3个输入。如下图所示, Softmax层将输入(a1, a2, a3)正规化,输出(y1,
y2, y3)。 Cross Entropy Error层接收Softmax的输出(y1, y2, y3)和监督标签(t1,t2, t3),从这些数据中输出损失L

Softmax层的反向传播得到了(y1 − t1, y2 − t2, y3 − t3)这样“漂亮”的结果。由于(y1, y2, y3)是Softmax层的输出,(t1, t2, t3)是监督数据,所以(y1 − t1, y2 − t2, y3 − t3)是Softmax层的输出和监督标签的差。
具体证明过程请参见 CSDN:简单易懂的softmax交叉熵损失函数求导
使用交叉熵误差作为 softmax函数的损失函数后,反向传播得到( y1 − t1, y2 − t2, y3 − t3)这样“漂亮”的结果。实际上,这样“漂亮” 的结果并不是偶然的,而是为了得到这样的结果,特意设计了交叉熵误差函数。
回归问题中输出层使用“恒等函数”,损失函数使用“平方和误差”,也是出于同样的理由。也就是说,使用“平方和误差”作为“恒等函数”的损失函数,反向传播才能得到( y1 −t1, y2 − t2, y3 − t3)这样“漂亮”的结果。
误差反向传播法的优点
误差反向传播算法可以计算输出目标函数 对所有的参数
的偏微分,这样就可以得到
相对于网络参数的梯度
,有了这个梯度,我们就可以使用梯度下降法对网络进行训练,即每次沿着梯度的负方向(
)移动一小步,不断重复,直到网络输出误差最小。
权重(和偏置)微小变化的传播,会最终传播影响到输出层。实际上,反向传播算法就是追踪权重(和偏置)的这种微小的变化是如何影响到损失函数的技术。
反向传播算法的特点是效率高。反向传播可以同时计算所有的偏导数,仅仅使用一次前向传播,加上一次后向传播。假设对一个节点求偏导需要的时间为单位时间,运算时间呈线性关系,那么网络的时间复杂度如下式所示:O(Network Size)=O(V+E),V为节点数、E为连接边数。为了提高反向传播算法的效率,我们通过高度并行的向量,利用GPU进行计算。
下一章,我们将介绍神经网络的学习中的一些重要观点,涉及寻找最优权重参数的最优化方法、权重参数的初始值、超参数的设定方法以及权值衰减、Dropout等正则化方法。
References:





















 484
484











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








