ccc-sklearn-11-线性回归（1）

1.线性回归概述

回归需求在现实中非常多，自然也有了各种回归算法。最著名的就是线性回归和逻辑回归，衍生出了岭回归、Lasso、弹性网，以及分类算法改进后的回归，如回归树、随机森林回归、支持向量回归等，一切基于特征预测连续型变量的需求都可以使用回归。
sklearn中的线性回归
linear_model模块包含了多种多样的类和函数。具体如下：

类/函数	含义
普通线性回归
linear_model.LinearRegression	使用普通最小二乘法的线性回归
岭回归
linear_model.Ridge	岭回归，一种将L2作为正则化工具的线性最小二乘回归
linear_model.RidgeCV	带交叉验证的岭回归
linear_model.RidgeClassifier	岭回归的分类器
linear_model.RidgeClassifierCV	带交叉验证的岭回归的分类器
linear_model.ridge_regression	【函数】用正太方程法求解岭回归
LASSO
linear_model.Lasso	Lasso，使用L1作为正则化工具来训练的线性回归模型
linear_model.LassoCV	带交叉验证和正则化迭代路径的Lasso
linear_model.LassoLars	使用最小角度回归求解的Lasso
linear_model.LassoLarsCV	带交叉验证的使用最小角度回归求解的Lasso
linear_model.LassoLarsIC	使用BIC或AIC进行模型选择的，使用最小角度回归求解的Lasso
linear_model.MultiTaskLasso	使用L1 / L2混合范数作为正则化工具训练的多标签Lasso
linear_model.MultiTaskLassoCV	使用L1 / L2混合范数作为正则化工具训练的，带交叉验证的多标签Lasso
linear_model.lasso_path	【函数】用坐标下降计算Lasso路径
弹性网
linear_model.ElasticNet	弹性网，一种将L1和L2组合作为正则化工具的线性回归
linear_model.ElasticNetCV	带交叉验证和正则化迭代路径的弹性网
linear_model.MultiTaskElasticNet	多标签弹性网
linear_model.MultiTaskElasticNetCV	带交叉验证的多标签弹性网
linear_model.enet_path	【函数】用坐标下降法计算弹性网的路径
最小角度回归
linear_model.Lars	最小角度回归（Least Angle Regression，LAR）
linear_model.LarsCV	带交叉验证的最小角度回归模型
linear_model.lars_path	【函数】使用LARS算法计算最小角度回归路径或Lasso的路径
正交匹配追踪
linear_model.OrthogonalMatchingPursuit	正交匹配追踪模型（OMP）
linear_model.OrthogonalMatchingPursuitCV	交叉验证的正交匹配追踪模型（OMP）
linear_model.orthogonal_mp	【函数】正交匹配追踪（OMP）
linear_model.orthogonal_mp_gram	【函数】Gram正交匹配追踪（OMP）
贝叶斯回归
linear_model.ARDRegression	贝叶斯ARD回归。ARD是自动相关性确定回归（Automatic Relevance DeterminationRegression），是一种类似于最小二乘的，用来计算参数向量的数学方法。
linear_model.BayesianRidge	贝叶斯岭回归
其他回归
linear_model.PassiveAggressiveClassifier	被动攻击性分类器
linear_model.PassiveAggressiveRegressor	被动攻击性回归
linear_model.Perceptron	感知机
linear_model.RANSACRegressor	RANSAC（RANdom SAmple Consensus）算法
linear_model.HuberRegressor	胡博回归，对异常值具有鲁棒性的一种线性回归模型
linear_model.SGDRegressor	通过最小化SGD的正则化损失函数来拟合线性模型
linear_model.TheilSenRegressor	Theil-Sen估计器，一种鲁棒的多元回归模型

2.多元线性回归LinearRegression

基本原理
回归结果方程如下：
$$\widehat{y_i}=w_0+w_1{x}_{i1}+w_2{x}_{i2}+\cdots w_n{x}_{in}$$
$w$称为模型的参数，$w_0$为截距，$w_1-w_n$为回归系数。如果有m样本，结果可以写作为：
$$\hat{\mathbf{y}}=w_0+w_1{\mathbf{x}}_{i1}+w_2{\mathbf{x}}_{i2}+\cdots w_n{\mathbf{x}}_{\mathbf{in}}$$
加粗的y包含了m个全部样本的回归结果的列向量。有$\hat{\mathbf{y}}=\mathbf{Xw}$

在多元线性回归中，定义损失函数如下：
$$\sum _{i=1}^m(y_i-\widehat{y_i}{)}^2=\sum _{i=1}^m(y_i-{\mathbf{X}}_{\mathbf{i}}\mathbf{w}{)}^2$$
其中，yi为样本i对应的真实标签，yhat就是一组参数w下的预测标签。该损失函数表达了向量$y-\widehat{y_i}$的L2范式的平方结果，L2范式的本质就是欧式距离。追求差异越小越好，即：
$${\underset{w}{\min }||\mathbf{y}-\mathbf{Xw}|{|}_2}^2$$
这个式子一般称为SSE（Sum of Sqaured Error，误差平方和）或者RSS（Residual Sum of Squares 残差平方和）

最小二乘法求解多元性=线性回归的参数
首先对w求导有：

转置化简并且乘法展开：

矩阵求导规则如下：

代入原式可得：

化简得到最终需要的w：

手动推导上面过程是基本要求，要经常复习加深理解。

3.简单的一次回归实验

参数	含义
fit_intercept	布尔值，可不填，默认为True 是否计算此模型的截距。如果设置为False，则不会计算截距
normalize	布尔值，可不填，默认为False 当fit_intercept设置为False时，将忽略此参数。如果为True，则特征矩阵X在进入回归之前将会被减去均值（中心化）并除以L2范式（缩放）
copy_X	布尔值，可不填，默认为True 如果为真，将在X.copy()上进行操作，否则的话原本的特征矩阵X可能被线性回归影响并覆盖
n_jobs	整数或者None，可不填，默认为None 用于计算的作业数。只在多标签的回归和数据量足够大的时候才生效。除非None在joblib.parallel_backend上下文中，否则None统一表示为1。如果输入 -1，则表示使用全部的CPU来进行计算

步骤一：导入库和数据

from sklearn.linear_model import LinearRegression as LR
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_score
from sklearn.datasets import fetch_california_housing as fch
import pandas as pd

housevalue = fch()
X = pd.DataFrame(housevalue.data)
y = housevalue.target
X.head(3)
X.shape
y

步骤二：分训练集和测试集

#列名更改为对应的特征
X.columns = housevalue.feature_names

Xtrain , Xtest, Ytrain ,Ytest = train_test_split(X,y,test_size=0.3,random_state=420)
#重置索引
for i in [Xtrain,Xtest]:
    i.index = range(i.shape[0])
Xtrain.shape
"""
MedInc：该街区住户的收入中位数
HouseAge：该街区房屋使用年代的中位数
AveRooms：该街区平均的房间数目
AveBedrms：该街区平均的卧室数目
Population：街区人口
AveOccup：平均入住率
Latitude：街区的纬度
Longitude：街区的经度
"""

步骤三：建模并探索模型

属性	含义
coef	数组，形状为 (n_features, )或者(n_targets, n_features) 线性回归方程中估计出的系数。如果在fit中传递多个标签（当y为二维或以上的时候），则返回的系数是形状为（n_targets，n_features）的二维数组，而如果仅传递一个标签，则返回的系数是长度为n_features的一维数组
intercept_	数组，线性回归中的截距项

reg = LR().fit(Xtrain,Ytrain)
yhat = reg.predict(Xtest)
yhat

reg.coef_
[*zip(Xtrain.columns,reg.coef_)]
reg.intercept_

步骤四：模型评估
回归算法中有两种角度来看待回归的效果：

1. 是否预测到了正确的数值
2. 是否拟合到了足够的信息

从第一个角度评估
残差平方和RSS本质是预测值和真实值之间的差异，也就是从第一个角度来评估回归能力。但是RSS是一个无界的值，并不能有一个准确的概念来判断效果。因此sklearn中使用MSE（mean squared error）来衡量预测值和真实值的差异：
$$MSE=\frac{1}{m}\sum _{i=1}^m(y_i-\widehat{y_i{)}^2}$$
本质就是RSS基础上除以样本总量，得到平均误差。

from sklearn.metrics import mean_absolute_error as MSE
MSE(yhat,Ytest)

y.max()
y.min()
cross_val_score(reg,X,y,cv=10,scoring="neg_mean_squared_error")

sklearn中认为均方误差是一种loss所以都用负数表示

从第二个角度来评估

上图中，红色为真实标签，蓝色是拟合模型。可以看到后半段的拟合效果十分糟糕，此时用第一种方式评估MSE会比较好，但如果我们需要一个拟合信息足够的模型就需要另一个评判指标即$R^2$:
$$R^2=1-\frac{{\sum }_{i=0}^m(y_i-\widehat{y_i}{)}^2}{{\sum }_{i=0}^m(y_i-\overline{y_i}{)}^2}=1-\frac{RSS}{{\sum }_{i=0}^m(y_i-\overline{y_i}{)}^2}$$
其中y是真实标签，yhat是预测结果，ybar是均值，yi-ybar除以样本量m是方差。分子是真实值和预测值之差的差值，也就是没有捕获的信息总量，分母是真实标签所带的信息量，所以其衡量的是1-我们模型没有捕获到的信息量占真实标签中所带信息量的比例，所以结果越接近1越好。

from sklearn.metrics import r2_score
r2_score(yhat,Ytest)

r2 = reg.score(Xtest,Ytest)
r2

r2_score(Ytest,yhat)
cross_val_score(reg,X,y,cv=10,scoring="r2").mean()

使用metrcis模块要注意参数的顺序，否则会出现相同指标但是结果不同。

import matplotlib.pyplot as plt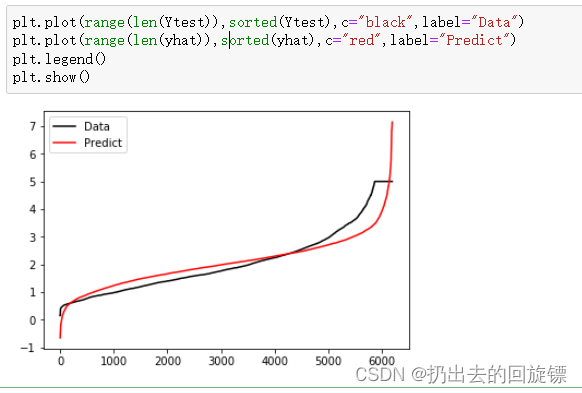![在这里插入图片描述](https://img-blog.csdnimg.cn/da9f1254a3804bf8a4b3396f4d56491b.png)

plt.plot(range(len(Ytest)),sorted(Ytest),c="black",label="Data")
plt.plot(range(len(yhat)),sorted(yhat),c="red",label="Predict")
plt.legend()
plt.show()

从图像上可以看到，虽然大部分数据拟合的不错，但开头和结尾差异缺比较大。若果此时图像右侧还有更多数据，则模型会偏离的越来越远。这个结果也反映了的计算出来的$R^2$值不高

误区注意-$R^2$可以为负！！！
解释平方和ESS（Explained Sum of Squares):定义预测值和样本均值之间的差异
总离差平方和TSS（Total Sum of Squares):定义真实值和样本均值之间的差异

然而公式TSS=RSS+ESS不是一直成立，证明如下：

可以看到，如果让$2{\sum }_{i=0}^m(y_i-\widehat{y_i})(\widehat{y_i}-\overline{y_i})$为负就可能让结果为负

横线是ybar，橙线是yhat，蓝色点是样本点。对$x_i$来说$(y_i-\widehat{y_i})>(\widehat{y_i}-\overline{y_i})$。即此时的模型几乎没有作用，不如全部算平均值。所以当模型结果$R^2$为负数时，证明拟合的很糟糕，需要调整或换其它算法。

4.岭回归与Lasso

多重共线性
矩阵的精确相关关系和高度相关关系并称为“多重共线性”，在多重共线性下，模型无法建立。一个满秩矩阵不能存在多重共线性。

由于多重共线性会导致模型极大的偏移，无法模拟数据的全貌，一般有三种处理多重共线性的方法：

使用统计学的先验思路	使用向前逐步回归	改进线性回归
在开始建模之前先对数据进行各种相关性检验，如果存在多重共线性则可考虑对数据的特征进行删减筛查，或者使用降维算法对其进行处理，最终获得一个完全不存在相关性的数据集	逐步归回能够筛选对标签解释力度最强的特征，同时对于存在相关性的特征们加上⼀个惩罚项，削弱其对标签的贡献，以绕过最小二乘法对共线性较为敏感的缺陷	在原有的线性回归算法基础上进行修改，使其能够容忍特征列存在多重共线性的情况，并且能够顺利建模，且尽可能的保证RSS取得最小值

岭回归，Lasso，弹性网就是依据第三种方法研究出来改善多重共线性的算法。

岭回归解决问题原理
岭回归，又称为吉洪诺夫正则化（Tikhonov regularization），完整表达式：
$$\underset{w}{\min }{||Xw-y|{|}_2}^2+{\alpha ||w|{|}_2}^2$$
即在多元线性回归的损失函数上加上了正则项，表达为系数$w$的L2范式乘以正则化系数$\alpha$，此时假设特征矩阵结构为（m，n），系数w的结构是（1，n），则有：

此时可以控制$\alpha$让$(X^{T}X+\alpha I)$可逆，此时w可以写作：

当然， $\alpha$挤占了w中由原始的特征矩阵贡献的空间，因此如果太大，也会导致w的估计出现较大的偏移，无法正确
拟合数据的真实面貌。

linear_model.Ridge 的使用

步骤一：导入库和数据并处理列名（和之前一样）

import numpy as np
import pandas as pd
from sklearn.linear_model import Ridge, LinearRegression,Lasso
from sklearn.model_selection import train_test_split as TTS
from sklearn.datasets import fetch_california_housing as fch
import matplotlib.pyplot as plt

housevalue = fch()
X=pd.DataFrame(housevalue.data)
y=housevalue.target
X.columns = housevalue.feature_names
X.head()

步骤二：划分训练集并建模

Xtrain , Xtest, Ytrain, Ytest = TTS(X,y,test_size=0.3,random_state=420)
for i in [Xtrain,Xtest]:
    i.index = range(i.shape[0])
    
reg = Ridge(alpha=1).fit(Xtrain,Ytrain)
reg.score(Xtest,Ytest)

步骤三：线性回归与岭回归交叉验证对比（$R^2$）

alpharange = np.arange(1,1001,100)
ridge, lr =[],[]
for alpha in alpharange:
    reg = Ridge(alpha=alpha)
    linear = LinearRegression()
    regs = cross_val_score(reg,X,y,cv=5,scoring="r2").mean()
    linears = cross_val_score(linear,X,y,cv=5,scoring="r2").mean()
    ridge.append(regs)
    lr.append(linears)
plt.plot(alpharange,ridge,color="red",label="Ridge")
plt.plot(alpharange,lr,color="orange",label="LR")
plt.title("Mean")
plt.legend()
plt.show()
#细化学习曲线
alpharange = np.arange(1,201,100)
ridge, lr =[],[]
for alpha in alpharange:
    reg = Ridge(alpha=alpha)
    linear = LinearRegression()
    regs = cross_val_score(reg,X,y,cv=5,scoring="r2").mean()
    linears = cross_val_score(linear,X,y,cv=5,scoring="r2").mean()
    ridge.append(regs)
    lr.append(linears)
plt.plot(alpharange,ridge,color="red",label="Ridge")
plt.plot(alpharange,lr,color="orange",label="LR")
plt.title("Mean")
plt.legend()
plt.show()

可以看到，在这个数据集上，岭回归结果先轻微上升，随后骤降。因此该数据集有轻微的共线性，但如果正则化程度太重，挤占参数w本来的估计空间。

步骤四：线性回归与岭回归交叉验证对比（$Variance$）

alpharange = np.arange(1,1001,100)
ridge, lr =[],[]
for alpha in alpharange:
    reg = Ridge(alpha=alpha)
    linear = LinearRegression()
    varR = cross_val_score(reg,X,y,cv=5,scoring="r2").var()
    varLR = cross_val_score(linear,X,y,cv=5,scoring="r2").var()
    ridge.append(varR)
    lr.append(varLR)
plt.plot(alpharange,ridge,color="red",label="Ridge")
plt.plot(alpharange,lr,color="orange",label="LR")
plt.title("Variance")
plt.legend()
plt.show()

可以看到消除多重共线性也许能够一定程度上提高模型的泛化能力。

多重共线性更加明显的数据对比

from sklearn.datasets import load_boston
from sklearn.model_selection import cross_val_score

X = load_boston().data
y = load_boston().target

Xtrain,Xtest,Ytrain,Ytest = TTS(X,y,test_size=0.3,random_state=420)
#方差的变化
alpharange = np.arange(1,1001,100)
ridge, lr =[],[]
for alpha in alpharange:
    reg = Ridge(alpha=alpha)
    linear = LinearRegression()
    varR = cross_val_score(reg,X,y,cv=5,scoring="r2").var()
    varLR = cross_val_score(linear,X,y,cv=5,scoring="r2").var()
    ridge.append(varR)
    lr.append(varLR)
plt.plot(alpharange,ridge,color="red",label="Ridge")
plt.plot(alpharange,lr,color="orange",label="LR")
plt.title("Variance")
plt.legend()
plt.show()
#R2变化
alpharange = np.arange(1,1001,100)
ridge, lr =[],[]
for alpha in alpharange:
    reg = Ridge(alpha=alpha)
    linear = LinearRegression()
    regs = cross_val_score(reg,X,y,cv=5,scoring="r2").mean()
    linears = cross_val_score(linear,X,y,cv=5,scoring="r2").mean()
    ridge.append(regs)
    lr.append(linears)
plt.plot(alpharange,ridge,color="red",label="Ridge")
plt.plot(alpharange,lr,color="orange",label="LR")
plt.title("Mean")
plt.legend()
plt.show()
#学习曲线细化
alpharange = np.arange(100,300,10)
ridge,lr=[],[]
for alpha in alpharange:
    reg = Ridge(alpha=alpha)
    regs = cross_val_score(reg,X,y,cv=5,scoring="r2").mean()
    ridge.append(regs)
    lr.append(linears)
plt.plot(alpharange,ridge,color="red",label="Ridge")
plt.title("Mean")
plt.legend()
plt.show()

可以看到使用岭回归让方差和偏差都明显降低了。升高了模型的泛化能力。可惜的是，大多数数据集在发布的时候都经过多重线性的处理，要找到多重共线性强的数据集非常困难，这也是导致岭回归和Lasso在机器学习领域冷遇的一部分原因。

Lasso 与多重共线性
Lasso全称（least absolute shrinkage and selection operator），同样被用来解决多重共线性的算法。Lasso使用系数w的L1范式（绝对值）乘以正则化系数$\alpha$，损失函数表达式为：
$$\underset{w}{\min }||Xw-y|{|}^2+\alpha ||w|{|}_1$$
通过最小二乘法求解参数W过程：

注意，Lasso无法解决特征值“精确相关”的问题，如果线性回归无解或者出现报除零错误，Lasso不能解决问题

当方阵$X^{T}X$存在时，有：
$$w=(X^{T}X{)}^{-1}(X^{T}y-\frac{\alpha I}{2})$$
其中$\alpha$可以取正数和负数，绝对值越大对于共线性的限制也越大。
使用Lasso进行特征选择

sklearn 中Lasso使用损失函数为：
$$\underset{w}{\min }\frac{1}{2n_{samples}}||Xw-y|{|}^2+\alpha ||w|{|}_1$$
添加的系数用于简便计算（求平均，统一系数）

比较$\alpha$参数对于Ridge，LinearRegression，Lasson的影响
准备工作

import numpy as np
import pandas as pd
from sklearn.linear_model import Ridge,LinearRegression,Lasso
from sklearn.model_selection import train_test_split as TTS
from sklearn.datasets import fetch_california_housing as fch
import matplotlib.pyplot as plt

housevalue = fch()
X = pd.DataFrame(housevalue.data)
y = housevalue.target
X.columns = ["住户收入中位数","房屋使用年代中位数","平均房间数目","平均卧室数目","街区人口","平均入住率","街区的纬度","街区的经度"]
X.head(3)

Xtrain,Xtest,Ytrain,Ytest = TTS(X,y,test_size=0.3,random_state=420)
for i in [Xtrain,Xtest]:
    i.index = range(i.shape[0])

正则系数为0时的情况

reg = LinearRegression().fit(Xtrain,Ytrain)
(reg.coef_*100).tolist()

Ridge_ = Ridge(alpha=0).fit(Xtrain,Ytrain)
(Ridge_.coef_*100).tolist()

Lasso_ = Lasso(alpha=0).fit(Xtrain,Ytrain)
(Lasso_.coef_*100).tolist()

三者结果几乎没有差距，Lasso中报错分别为：

1. 正则化系数不能为0
2. 不鼓励没有正则项的坐标下降法
3. 目标函数不收敛，使用非常小的$\alpha$可能导致精度问题

但是用非0的小$\alpha$时的各个结果

Ridge_ = Ridge(alpha=0.01).fit(Xtrain,Ytrain)
(Ridge_.coef_*100).tolist()

Lasso_ = Lasso(alpha=0.01).fit(Xtrain,Ytrain)
(Lasso_.coef_*100).tolist()

稍微改变alpha参数的值，Lasso就产生了明显的变换。实际上，Lasso对于系数的惩罚也确实重的多，并且会导致系数压缩到0，这也导致实际使用中让Lasso的正则化系数在很小的空间中变动

Lasso选取最佳的正则化化参数取值

正则化系数由正则化路径进行变动：

对于x1,x2,x3,…xn这n个特征，每个$\alpha$可以取得一组对应的参数向量，其中包含了n+1个参数，分别是$w_0,w_1,...w_n$。看作是n+1维空间的一个点，对于不同的$\alpha$取值，将得道许多（n+1）的点，这些点形成的序列，就被称为正则化路径，$\frac{a.min}{a.max}$被称为正则化路径的长度

sklearn中通过规定正则化路径的长度、$\alpha$的个数来让sklearn为我们自动生成取值。LassonCV会单独建立模型，首先找出最佳的正则化参数，然后在这个参数下按照模型评估建模

参数	含义
eps	正则化路径的长度，默认0.001
n_alphas	正则化路径中 的个数，默认100
alphas	需要测试的正则化参数的取值的元祖，默认None。当不输入的时候，自动使用eps和n_alphas来自动生成带入交叉验证的正则化参数
cv	交叉验证的次数，默认3折交叉验证，将在0.22版本中改为5折交叉验证
属性	含义
alpha_	调用交叉验证选出来的最佳正则化参数
alphas_	使用正则化路径的长度和路径中 的个数来自动生成的，用来进行交叉验证的正则化参数
mse_path	返回所以交叉验证的结果细节
coef_	调用最佳正则化参数下建立的模型的系数

准备工作

from sklearn.linear_model import LassoCV
#建立alpha参数选择的范围
alpharange = np.logspace(-10, -2 , 200 , base=10)
alpharange.shape
Xtrain.head(2)

模型与结果

lasso_ = LassoCV(alphas=alpharange
                ,cv=5
                ).fit(Xtrain,Ytrain)
#查看被选择出来最佳正则化系数             
lasso_.alpha_
#调用所有交叉验证的结果
lasso_.mse_path_
lasso_.mse_path_.shape
#返回每个alpha取值下交叉验证的结果，因此axis=1，跨列求均值
lasso_.mse_path_.mean(axis=1)
#最佳正则化系数下获得的模型系数结果
lasso_.coef_
lasso_.score(Xtest,Ytest)

与线性回归对比

reg = LinearRegression().fit(Xtrain,Ytrain)
reg.score(Xtest,Ytest)

ls_  = LassoCV(eps=0.00001
              ,n_alphas=300
              ,cv=5
              ).fit(Xtrain,Ytrain)
ls_.alpha_ 
ls_.alphas_
ls_.alphas_.shape
ls_.score(Xtest,Ytest)
ls_.coef_