算法与数据结构简介

1、  数据结构简介

数据结构是对计算机中所保存数据的一种组织和存放方式，每一种不同的数据结构都会将数据按某种方式来保存。并且按特定的方式进行操作，相对零散地保存数据，使用经过精心设计的各种数据结构，有助于更有效地使用数据和各种算法，能用最少的资源、最短的执行时间、最小的存储空间完成各种关键操作和任务。

数据结构是将数据存储到计算机中的一种方式，以便有效使用这些数据。

经过精心设计的每种数据结构都有一些独特的属性，使其适用于解决各种不同的问题。

数据结构的各种类型如下：

栈。

队列。

链表。

哈希表。

树。

堆。

图。

1.1、栈

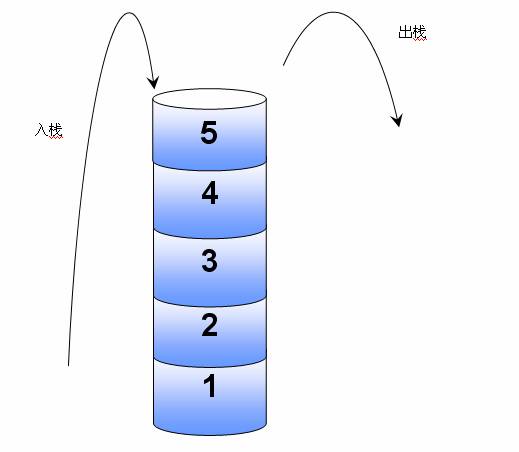
定义：我们把在存储数据时按后进先出（Last In First Out，LIFO）原理工作的一种数据结构称为“栈”。

当我们使用栈来保存数据时，最先被保存的数据，只能在最后取出，最后保存的数据，将被最先取出。

如图：我们假设编号为1、2、3、4、5的小圆盘为栈中保存的每一个数据，其中小圆盘1首先装入，小圆盘5最后装入，而在取数据时就必须先取出小圆盘5，才能取下面得，最后才能取出小圆盘1。

 

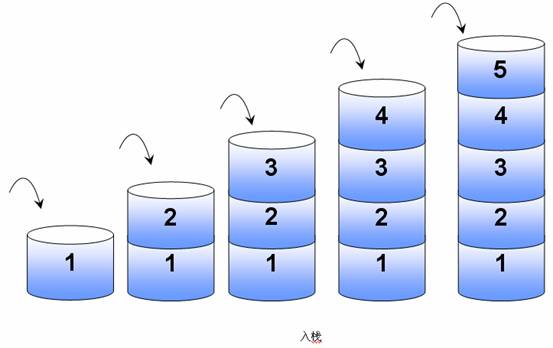
入栈：入栈又称为“压栈”，把数据保存到栈中。该操作是将一个数据添加到栈中，或称为压入栈顶，这时栈的大小就加1。

如图：每次将一个小圆盘装到另一个上面，首先装入的是小圆盘1，然后装入小圆盘2、小圆盘3、小圆盘4，最后装入小圆盘5。

 

 

 

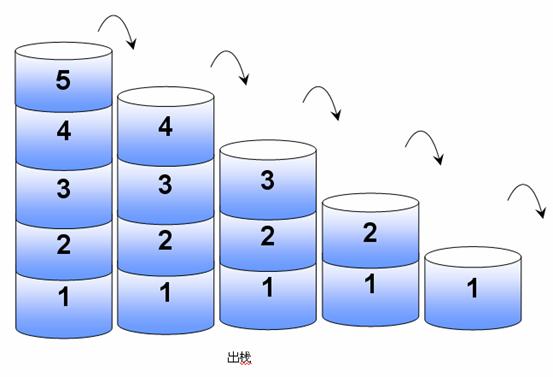
出栈：从栈中取出数据。在此操作中每个数据逐个弹出，直到栈变为空。

如图：位于栈顶的小圆盘5首先从栈中弹出，栈的大小减1.该过程一直继续，栈的大小递减为3，然后递减为2，直到栈为空。

 

栈的应用：

在实际的计算机应用中，很多地方都会用到栈的结构来保存和处理数据，比如处理回文验证、数制转换、表达式求值、括号匹配检验、行编辑程序、递归实现等。

如：将十进制数字转换为二进制

方法：将十进制数不断除2 取余数

      

 

 

 

在使用计算机完成计算时，最先求出的余数需要最后显示出来，而最后求出的余数最先显示出来

       符合栈的先入后出性质，故可用栈来保存求出的所有余数，最后再依次显示出来

十进制转二进制方法：将十进制数不断除2 取余数，（数字除2，看余数，从最后一个余数读起）

       二进制转十进制方法：n X 2几次方+……

       如：95转换为二进制位101’1111。

              将二进制数字101’1111转换为十进制：

              给二进制从右向左标记位数，从0开始标记，101’1111标记为：

 

1.2、队列

定义：我们把存储数据时按先进先出（First In First Out,，FIFO）原理工作的一种数据结构称为“队列”。当我们使用队列来保存数据时，最先被保存的数据会被最先取出，最后保存的数据则最后取出。队列只允许从一端访问。

如图：在我们平常的生活中，也能发现很多类似队列结构的情形：以在银行排队为例，当顾客取银行办事时，他们站在队伍末尾排队，在获得所需服务后，队伍前面的人先出来。（排在前面的人，先进行处理）。在比如：火车进山洞（隧道）的的时候，先进隧道的车厢，最先出隧道。队列操作很像穿过隧道的火车。即火车头首先进入隧道，各节车厢随后依次进入隧道。

 

 

 

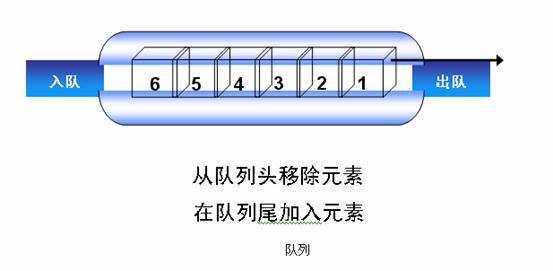
入队：入队就是把数据保存到队列中。入队操作将数据加入到队列尾。

如图:第一个数据从末尾入队，然后第二个数据也入队，并向前移动，直到第5个数据也入队为止。

 

 

 

 

出队：出队就是从队列中取出数据。出队操作从队列移除数据。

如图：第一个数据从队列头出队，然后是第二个数数据。类似地，这个过程一直继续到最后一个数据出队。

 

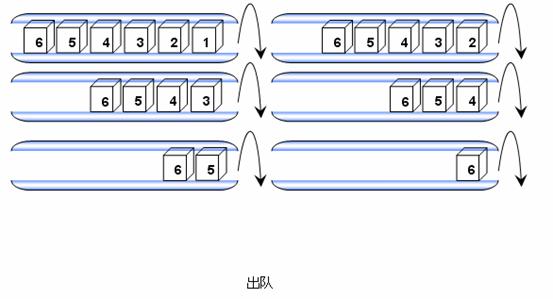
队列的应用：操作系统中就使用了队列这种数据结构，当我们向操作系统发出很多任务或指令后，操作系统并不能把它们立即都完成，但也不是无序地随意执行，而是按一定顺序完成。原因就在于这些指令被保存在一个队列的结构中，先被保存的指令将先被取出、先被执行。

队列还被广泛地应用在多关键字排序、解决主机与外部设备之间速度不匹配问题、解决多用户引起的资源竞争问题、最短路径问题、迷宫问题等各个方面。

 

2、  常用算法

       算法：算法是逐步解决指定问题的步骤和方法。有限性、明确性。

       计算机中常用的算法 ：求最大值、最小值 和 平均值

2.1、求最大值

由于开始时并不知道最高分，所以在要比较的数当中取一个数，将该数当作临时最大数，并且存储在临时变量“i”中。然后将其他数一一分别与这个数比较，如果比这个数大，就将该数存储到临时变量“i”中，然后继续比较其他数，直到全部比较完毕。此时临时变量“i”中的值就是最大数。

求最小值

与求最大值方法一样。

2.2、查找

查找是从较大的数据集中找出或定位某些数据(比如字母、词语、文件和网站等)的过程。

2.2.1、线性查找

在一列给定的值中进行搜索，从一端开始逐一检查每个元素，直到找到所需元素，这个过程叫做线性查找。线性查找又称为顺序查找。

       线性查找可用于有序列表，也可以用于无序列表。

2.2.2、二分查找

       二分查找法是在一个有序的元素列表中查找具有特定值的元素的一种方法。

       将有序列表的中间元素与被查找的值进行比较。

如果中间元素小于被查找的值，排除该有序列表的前半部分，然后对其剩余部分执行相同的过程。

如果中间元素大于被搜索的值，则知道该值一定在中间元素前面的某处。

2.3、排序方法

       排序：排序是把一组无序的数据按照递增或递减的次序重新排列的过程。

2.3.1、冒泡排序

冒泡排序：冒泡排序是一种简单的排序算法。此方法将一个列表中的两个元素进行比较，并将最小的元素交换到顶部。

从最底部的元素开始比较。

两个元素中较小的会冒到顶部，而较大的会沉到底部。 

该过程将被重复执行，直到所有元素都被排序。

该排序过程的名称就说明乐其工作方式，我们把较小的数类比成气泡，气泡会不断向上冒，越小的数就冒得越高，最终达到排序的效果。此方法要先从底层元素开始，用它比较和它紧挨着的上一个元素，将两个元素进行比较，如果下面元素小于上面元素，则交换它们，否则保持原样。然后转移到最底层的上一个位置，重复以上过程，最后，最小的元素将从其原始位置冒到顶部。这时我们再从最底层元素开始比较，重复前面把最小值放在最顶端的步骤，就可以将第二小的值放在第二个位置了，如此不断重复，直到这组数据中的所有元素都被排序。

如：将5个数进行升序排序（从小到大）。

（1）、将第五个元素的值与第四个元素的值进行比较。

（2）、如果第五个元素的值小于第四个元素的值，则交换这两个元素的值。

（3）、接下来，将第四个元素的值与第三个元素的值进行比较。如果上面元素的值大于下面元素的值，则交换他们的值。

（4）、将第三个元素的值与第二个元素的值进行比较，这样继续比较和交换的过程。

（5）、到此过程结束时，最小值到达第一个元素。以形象化得术语可描述为：具有最小值的气泡冒起来了。

（6）、在下一交换过程中，再次从最底层的元素开始比较，一直向上进行到第二个元素。由于第一个元素已经包含最小值，不需要与它比较。这样，第二小的元素就被冒到了第二个位置。

（7）、再次进行交换，分别将第三小和第四小的数冒到合适位置。

（8）、排序完成。

在排序过程结束时，较小的值冒起，而较大的值下沉。

2.3.2、插入排序

插入排序：检查数组列表中的每个元素，并将其放入已排序元素中的适当位置。在插入排序法中，一组数字中的每个元素在经过检查之后放入已经排序元素列表中的适当位置。当最后一个数字放入合适位置时，该组数据排序完毕。

如：假设一组数据有5个元素，对他们进行排序。

（1）、假定第一个元素的值已经排序。

（2）、将第二个元素的值与该数组的已排序部分（当前只含第一个元素）进行比较。

（3）、如果第二个元素的值更小，就将它插在第一个元素之前。此时，前两个元素组成已排序列表，其余元素组成未排序列表。

（4）、将未排序列表中的第一个元素（即第三个元素）与已排序列表比较。

（5）、如果第三个元素的值小于第一个元素，则第三个元素的值就插入到第一个元素之前。否则，如果第三个元素的值小于第二个元素，则第三个元素的值就插到第二元素之前。此时，该数组的已排序部分包含3个元素，而未排序部分包括两个元素。

（6）、将为排序部分的元素与已排序部分的元素进行比较的过程继续进行，直到数组中的最后一个元素完成比较为止。

在排序过程结束时，每个元素都插入到适当的位置中。