NP完全性理论简介

本文目录

• 算法时间复杂度
• P问题
• NP问题
• 归约
• NP完全问题
• P=NP?
• NP难问题
• 求解难问题

---

算法时间复杂度

       对于一个规模为n问题，我们通常用O(n)表示通过某种算法求解这个问题的时间复杂度。对于同一个问题，不同的算法可能会产生不同的复杂度。最典型的例子就是排序，对于n个整数，选择排序和冒泡排序的复杂度为O(n²)，快速排序的复杂度为O(nlogn)，而使用基数排序的复杂度仅为O(mn)。

       当数据的规模比较小时，由于现在的计算机的速度都比较快，因此显现不出差距。不过对于指数级和阶乘的复杂度来说，运行这些算法所消耗的时间会随着n的增加而骤增。假设我们拥有一台每秒钟可以执行100万次计算的机器，考虑n=50的情况下，执行复杂度为O(logn)的算法用时还不足十万分之一秒，执行复杂度为O(n²)的算法大约需要千分之一秒，对于复杂度为O(2ⁿ)的算法则需要36年，而执行一次复杂度为O(n!)的算法则要花费10^57(10的57次方)年！

       因此对于数据规模为n的问题，我们通常认为其算法复杂度为n的多项式时，该问题是存在有效解决方案的。对于这样的复杂度，称为多项式时间复杂度，显然O(2ⁿ)和O(n!)不属于多项式时间复杂度。

       这里额外说明一下，对于表达形式不是多项式的情形，在比较其复杂度时，可以将它与一个多项式相除，并求在n趋向于无穷大时的值（运用洛必达法则）。举个栗子，nlogn/n²在n→∞时为0，因此O(nlogn)复杂度低于O(n²)，这意味着对于O(nlogn)复杂度的问题也是存在有效解决方案的。

P问题

       这里P指代Polynomial。P问题是指能够在多项式时间内解决的问题，这意味着计算机能够在有限时间内完成计算。整数排序问题就是P问题，不管你是采用冒泡排序还是快速排序，也无论你是对于10个整数排序还是10亿个整数排序。

NP问题

       NP指的是(Nondeterministic Polynomial)，即非确定性多项式时间。NP问题是指我们能够在多项式时间内验证一个解的问题。

       对于一个问题，如果我们能够在多项式时间内解决，那么我们肯定也能在多项式时间内验证某个猜测是否为这个问题的一个解，因此P问题也属于NP问题，或者说P问题是NP问题的一个子集。

       不过更多的情况下，我们对于一些问题暂时没有能够在多项式时间内解决它的方案（当然可能永远也不会有，这样的方案是否存在将在下文讨论），但是我们能够在多项式时间内去验证一个解。下面举两个属于这种类型问题的例子。

       1、N皇后问题。在学习数据结构和算法这门课时，有一个比较经典的问题叫做“八皇后问题”，它要求在一个国际象棋的棋盘上摆放八个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上。这里我们把棋盘扩展到N*N，并在其中摆放N个皇后，其他要求一样。这个问题就是一个NP问题，至今为止暂时还没有多项式时间的解法。不过我们很容易验证一个解是否满足要求：对于这N个皇后中的每一个，都检查其所在行，所在列和两个斜线方向是否有其他皇后，即可验证这个解是否是正解，这种验证方法的复杂度为O(n)。

       2、划分问题。以下38个整数的和为2000000：

14175,15055,16616,17495,18072,19390,19731,
22161,23320,23717,26343,28725,29127,32257,
40020,41867,43155,46298,56734,57176,58306,
61848,65825,66042,68634,69189,72936,74287,
74537,81942,82027,82623,82802,82988,90467,
97042,97507,99564

       要求把它们平均分为两组，每组的19个数字之和都是1000000.

       求解这个题其实并不容易，把这38个数分为两组总共有17672631900种方式。也许求出结果对于当今的计算机来说并非遥不可及，程序稍微优化一些其实并不用枚举其中的每一种情况（比如取到前17个数就已经超过1000000时，不用再取第18个和第19个数了）。然而如果是把2000个数分为两组呢？恐怕世界上最好的计算机也无能为力了。

       不过，验证这个问题的解却非常容易，只需检验一下在同一组的19个数的和是不是1000000即可。

归约

       为了下文的阐述，这里需要介绍一下归约(Reducibility，也有一些书中称之为 “约化”)的概念。我们定义一个问题P可以归约到另一个问题Q，当解决Q的方法也可以用来解决P时。这也就是说，如果我找到了解决问题Q的算法，那么这个算法也可以解决问题P。因此我们可以知道问题P一定不比问题Q要难，至少它们两个是同样难度的。

       看下面两组问题。

1.a 已知北京，上海，深圳，昆明，长沙，武汉，西安，台湾这八座城市中任意两座城市之间的机票价格。现在隔壁老王从北京出发，飞到其他七座城市（每个城市都要去一趟），最后回到北京。求是否存在机票总开销小于10000块的旅行方案？

1.b 已知北京，上海，深圳，昆明，长沙，武汉，西安，台湾这八座城市中任意两座城市之间的机票价格。现在隔壁老王从北京出发，飞到其他七座城市（每个城市都要去一趟），最后回到北京。求所有旅行方案中机票总开销最少为多少钱？

2.a 现有N个人要乘坐电梯到楼上，他们的体重分别为a1,a2, … ,an，电梯足够宽敞，不过最大的载重为M，试问是否存在一种方案使得电梯往返次数不多于t次，并且将这N个人全部送上楼？

2.b 现有N个人要乘坐电梯到楼上，他们的体重分别为a1,a2, … ,an，电梯足够宽敞，不过最大的载重为M，要求设计一种方案将这N个人全部送上楼，并且电梯往返次数最少？
2.c 在某港口放有N个集装箱，它们需要通过海运送到另一港口。已知其中第i个集装箱的长宽高和重量分别为Li,Wi,Hi,Mi。负责运载的轮船其货仓的长宽高和载重分别为L,W,H,M。要求设计一种方案将这些集装箱全部海运到另一港口，并且使用的轮船数目最少。

       在第一组问题中，如果我们知道了问题1.b的解，那我们也就知道了问题1.a的解。并且用来求解问题1.b的方法也可用在求解问题1.a上。因此这组问题中，1.a可以归约到1.b

       同样，在第二组问题中，如果我们知道了问题2.b的解，那我们也就知道了问题2.a的解。如果我们能解出2.c，那么我们也一定能解出2.b，然后解出2.a。这里主要是想强调一下归约的可传递性：如果P可归约到Q，Q可归约到R，那么P可以归约到R。

NP完全问题

       那么有没有这样一种NP问题：所有的NP问题都可以归约到它。也就是说，解决了这个问题，也就同时解决了所有的NP问题。

       在1971年，斯蒂芬·库克找到了第一个这样的问题：可满足性问题。简要来说，就是对于N个布尔类型的变量，它们之间采用“与”，“或”，“非”这样的逻辑运算符连接，那么这些变量能否找到一组合适的取值，使得最终的运算结果为真。与之相同的是逻辑电路问题，它其实就是可满足性问题的数字电路实现，用高电平和低电平表示真和假，用与门，或门和非门表示逻辑运算符。

       伯克利的教授理查德·卡普在读过库克的论文之后，发现有一种方法可以把可满足性问题归约到团问题。团问题大致是这样一类问题：对于任意两个人，要么是微信好友，要么不是微信好友。那么能否找到一个人数为50个人的团体，使得他们两两之间彼此都是微信好友？因为库克证明了可满足性问题是NP问题中最难的问题，而卡普得到的则是，团问题不比可满足性问题要简单，至少它们一样难。卡普不仅证明了团问题是NP问题中最难的一个，而且他还找到了19个同样难度的重要问题，比如哈密顿回路，旅行商问题，最大割问题等等。1972年，他在他的论文《Reducibility Among Combinatorial Problems》中，提出了这21个NP中最难的问题。

       那么这些问题叫什么名字呢？在1973年，曾经做了一次投票调查，在投票中出现了几个候选项——herculean, formidable, arduous, intractable, obstinate等等，不过最终胜出的还是”NP-Complete”（NP完全）。complete表示完全或者完备，一个事实集合被称为是完备的，表明它能解释某些逻辑系统的所有真命题。这也比较符合解决了NP完全问题，就能解决所有其他的NP问题的事实。NP完全问题也简称为NPC问题。

P=NP?

       那么对于NP问题，是否都存在有效的解决方法呢？这个问题直到现在一直都没有结论。如果要证明P=NP，则只需给出任意一个NPC问题的多项式复杂度的解决方案即可，随后我们就能得出这样的结论：所有的NP问题都存在多项式复杂度的解决方案（包括上面提到的N皇后问题，划分问题），即使我们还没有发现这些解决方案究竟是什么。

       其实我本人还是倾向于P≠NP的，但是证明P≠NP则相当艰难。证明一件事情可以做到，则给出它的一种解决方案即可。而要证明不可能做成某一类事情，则需要给出所有这样问题在所有情况下都不存在高效的解决方案。

       现在的很多设计都是基于P≠NP之上的，那么假如某一天某一位大牛证明了P=NP，那将对我们的生活产生怎样的改变呢？举几个栗子。在生物学方面，我们能够很快地完成基因测序工作；对于一个机器学习系统，能够很快的得到令人满意的特征选择；如果从犯罪现场提取到罪犯的DNA，我们能在第一时间确定他是谁。不过，这也同样会带来问题：比如当前信息在网络传输中使用MD5来校验，以检查是否在中途被篡改，不过在P=NP之后，这种校验方式就不再可靠了。同样，对于RSA加密算法，也可以很快地计算出密钥。因为RSA是基于计算大数的乘法和除法很容易，而对大数进行因式分解非常难而设计的，因式分解被认为是NP问题。

NP难问题

       那么有没有比NPC问题还要难的问题呢？答案是有的。

       前面说过NPC问题是NP问题中最难的一类问题，那么比NPC问题还要难的问题是什么样子呢？首先可以由NPC问题归约到它，其次它不一定是NP问题。这一类问题称为NP难问题。

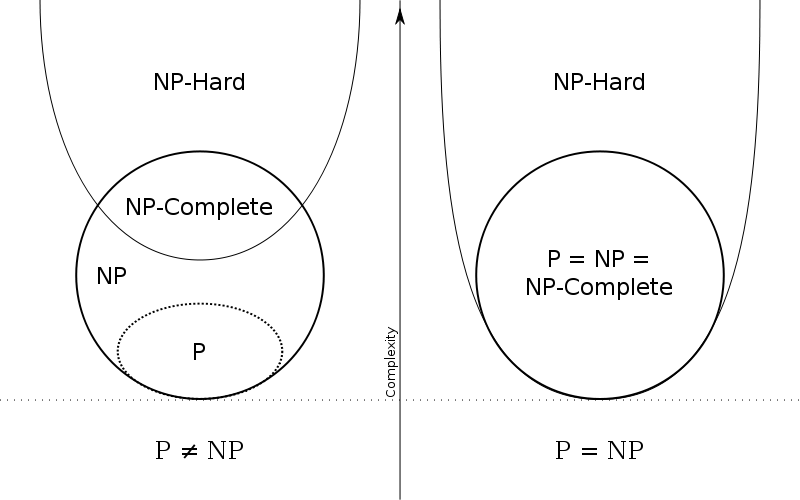
       这里要强调一下NP难问题本身并不一定是NP问题。如果一个问题可以由NPC问题归约到它（也就是说所有NP问题都可归约到它），那它就是NP难问题。更进一步，如果它本身也是NP问题的话，那么它就是NPC问题。就像我们刚才说的可满足性问题可以归约到团问题一样。NPC问题是NP难问题的一个子集。网上看到过一幅表明P问题，NP问题，NPC问题和NP难问题的关系图，觉得非常棒，这里引用过来。

       前面说过如果P=NP，那么所有的NP问题都存在有效的解决方案，而对于NP难问题来说，即使P=NP，也不一定存在有效的解决方案。

       围棋问题就是一个NP难问题。在一个围棋棋盘上摆出一个残局（其实只要棋盘上有棋子，都可以叫做残局），现在问如果执黑棋的选手每一步都选择在最优的位置下子，那么他是否一定能赢？这个问题没有人能在多项式时间内猜到一个必胜的下子位置并且证明它是对的，因为你的决策与对方的下子位置有关。而你的决策又会对对方下一步的下子位置产生影响，因此如此走下去，需要大量的时间和巨大的存储空间进行推导。

       我们前面在讨论“归约”时提出的那两组问题中，1.b, 2.b和2.c都是NP难问题，因为对于任意一个方案，我们很难在多项式时间内判定它是否是全局最优的，因此它们属于NPC问题范围之外的NP难问题。

       为了后面叙述，这里再举个栗子：在机器学习中会遇到特征选择的问题，当发现你的学习系统存在过拟合时，你可能会考虑要减少特征的数量。如果当前的输入特征数为n，那么需要从这些特征中选择一个子集。对于其中每一个特征，我们都可以选择留下它或者抛弃，那么一共会产生2ⁿ种方案。对于其中任意一种方案，通过训练样本，然后进行交叉验证得到一个效果的衡量，但我们很难通过这个衡量来验证这个方案是不是全局最优的，即一般性误差(generalization error)最小。因此普遍认为选取全局最优的特征子集是一个NP难问题。

求解难问题

       对于一个NP问题甚至是NP难问题，通常都无法找到有效的解决方案，于是隔壁老王跟老板说：这个问题我解决不了，并且你找任何人都解决不了。老板想了想之后，把隔壁老王开除掉了，毕竟谁都解决不了，那就干脆不雇佣人好了，还能省点儿钱。

       几天之后，有个叫小明的同学跟老板说：你交给隔壁老王的那个问题要求有些太高，现在没有人能解决。但是如果把要求稍微降低些，我能给你提供一个不错的解决方案。于是老板想了想觉得可以接受，于是就雇佣了小明，顶替隔壁老王之前的岗位。

       在遇到几乎不可能做到的问题时，我们通常会选择退而求其次，寻找一个还能说得过去的方案。

       比如我们要寻找从国贸到中关村的最短距离（当然这个问题使用穷举法也不会算太长时间，仅仅是举个栗子。如果你觉得不过瘾，可以考虑从杭州西湖到中关村的最短距离），由于中间的道路比较繁杂，穷举起来数目非常多，于是我们可以采用一种优化的方案：约定中途需要经过西直门。首先寻找从国贸到西直门的最短距离，然后寻找从西直门到中关村的最短距离。显然从国贸到中关村的最短距离，一定不会比从国贸到西直门的最短距离 加上 从西直门到中关村的最短距离要长。这么做虽然得到的可能不是最短距离的出行方案，不过却可以缩短我们的搜索范围，大大提高了解决问题的效率。当然，你还可以在国贸和西直门之间锁定另外一个地方，比如南锣鼓巷。很多地图软件就是采用这样的方案提供路线的。

       上面提到的机器学习中的特征选择问题，通常采取的做法是使用前向搜索这种启发式算法：每次从所有未选择的特征中选择一个使评价结果最佳的特征，加入到备选子集中，直到加入任何特征时评价结果无法更好，或者达到了限定的特征数。这样做不能保证达到全局最优，不过却使得实现起来变得可能。

结束语

       人们在证明P≠NP的道路上已经走过了数十年，目前仍没有得到一个有说服力的答案。如果要证明不存在有效的算法解决那些NP完全问题，不仅要指明现有的算法无法解决，还要论证未来发明的算法也无法解决，那么如何证明一个还没有出现的东西就必将失败呢？

       也许终有一天，有一位旷世奇才找到了打开宝箱的钥匙。不过在那之前，所有的科学家们还需要在这条荆棘路上摸索很长一段时间。