从波的角度理解图像和滤波

0 前言

在图像处理中滤波是一种很常用的操作，无论是去噪、模糊，还是锐化和提取边缘都是在进行滤波，只不过是使用的滤波器不同。为什么图像可以进行滤波呢，通常我们都是针对波来进行滤波的？其实图像也是一种波，只不过是二维的(灰度图像，彩色图像可以看成是三维的)，所以我们使用的滤波器也是二维的。我们常见的波，如声波是一维的，所使用的的滤波器一般也是一维的。

1 图像为什么是波呢

我们知道，图像由像素组成。下图是一张 400 x 400 的图片，一共包含了 16 万个像素点。

每个像素的颜色，可以用红、绿、蓝、透明度四个值描述，大小范围都是0 ～ 255，比如黑色是[0, 0, 0, 255]，白色是[255, 255, 255, 255]。通过 Canvas API 就可以拿到这些值。

如果把每一行所有像素（上例是400个）的红、绿、蓝的值，依次画成三条曲线，就得到了下面的图形。

可以看到，每条曲线都在不停的上下波动。有些区域的波动比较小，有些区域突然出现了大幅波动（比如 54 和 324 这两点）。

对比一下图像就能发现，曲线波动较大的地方，也是图像出现突变的地方。

这只是一维的情况，其实我们可以想象一下，如果根据像素的值画出二维的波形图，应该是三个三个曲面，RGB三个通道分别是一个曲面。

2 频率

我们知道波是有频率、波长、周期等物理量的，一般的图像不是有规律的特定波形，所以波长和周期暂时不进行研究。我们来看图像的频率。
图像就是色彩的波动：波动大，就是色彩急剧变化；波动小，就是色彩平滑过渡。因此，波的各种指标可以用来描述图像。

频率（frequency）是波动快慢的指标，单位时间内波动次数越多，频率越高，反之越低。

上图是函数sin(Θ)的图形，在2π的周期内完成了一次波动，频率就是1。

上图是函数sin(2Θ)的图形，在2π的周期内完成了两次波动，频率就是2。

所以，色彩剧烈变化的地方，就是图像的高频区域；色彩稳定平滑的地方，就是低频区域。

3 滤波

物理学对波的研究已经非常深入，提出了很多处理波的方法，其中就有滤波器（filter）：过滤掉某些波，保留另一些波。

下面是两种常见的滤波器 。

• 低通滤波器（lowpass）：减弱或阻隔高频信号，保留低频信号
• 高通滤波器（highpass）：减弱或阻隔低频信号，保留高频信号

下面是低通滤波的例子。

上图中，蓝线是原始的波形，绿线是低通滤波lowpass后的波形。可以看到，绿线的波动比蓝线小很多，非常平滑。

下面是高通滤波的例子。

上图中，黄线是原始的波形，蓝线是高通滤波highpass后的波形。可以看到，黄线的三个波峰和两个波谷（低频波动），在蓝线上都消失了，而黄线上那些密集的小幅波动（高频波动），则是全部被蓝线保留。

再看一个例子。

上图有三根曲线，黄线是高频波动，红线是低频波动。它们可以合成为一根曲线，就是绿线。

上图中，绿线进行低通滤波和高通滤波后，得到两根黑色的曲线，它们的波形跟原始的黄线和红线是完全一致的。

4 图像的滤波

图像的滤波与物理波的滤波是类似的，只不过是在二维(彩色图像也可以认为是三维)空间中进行的，要用的滤波器模板也是二维的。图像滤波是很多图像处理算法的预处理过程。

4.1 滤波的作用

消除图像中的噪声: 一般是使用低通滤波，噪声在图像中一般是高频信号。
为图像识别抽取出图像特征：这里的特征一般为边缘纹理的特征，一般是使用高通滤波，图像中边缘和纹理细节是高频信号。

4.2 滤波的分类

图像中滤波算法的分类有很多，除了上面介绍的低通和高通滤波器，还可以分为线性滤波和非线性滤波，可以分为相关滤波和卷积滤波，空间滤波和频域滤波。只不过是从不同的角度来进行解释，但是我个人认为，低通和高通滤波器这样的分类最能反映滤波器的本质。

4.2.1 线性滤波和非线性滤波

4.2.1.1 线性滤波

线性滤波： 维基百科解释为：用于时变输入信号的线性运算，在图像处理中可以这么理解，对于输入的信号（即要处理的图像),进行的是线性的运算，得出的结果作为输出图像。可以参考下图

首先有一个滤波器的模板（这里是3x3大小），模板里有系数，输出图像上f(x,y）的值等于模板系数与输入图像f(x,y)周围的像素点相乘求和，这个运算是线性的。在线性的滤波器中，运算的不同即为滤波器的系数模板不同。
线性滤波的包含: 方框滤波、均值滤波、高斯滤波、拉普拉斯滤波、sobel算子等。
方框滤波：
方框滤波，线性滤波里面最简单的一个。即用一个已确定的模板系数去与像素点邻域相乘，所得结果累加即为像素点的响应。

均值滤波：
均值滤波则是方框滤波的特例，将方框滤波的系数模板归一化之后便是均值滤波

可以看到，均值滤波的结果是取像素点周围领域的平均值作为响应输出。
高斯滤波：
高斯滤波的模板系数就稍显复杂，其模板系数是服从高斯分布的。
先看看一维的高斯分布和二维的高斯分布：

所以高斯滤波的模板系数，应该服从上图中的锥形山峰。那如何计算高斯分布的模板系数呢，我们取均值为模板的中心点，计算公式如下：

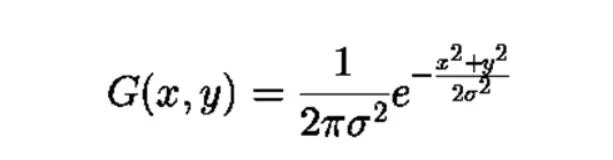
假如不想手动计算高斯滤波的模板系数，也可以取模板的近似值作为模板。如3x3和5x5的模板可以取

sobel算子
Sobel算子是典型的基于一阶导数的边缘检测算子，由于该算子中引入了类似局部平均的运算，因此对噪声具有平滑作用，能很好的消除噪声的影响。sobel算子对边缘定位不是很准确，图像的边缘不止一个像素；当对精度要求不是很高时，是一种较为常用的边缘检测方法。


一阶导数可以由差分来近似，可以求得Gx和Gy：



Canny算子
该算子功能比前面几种都要好，但是它实现起来较为麻烦，Canny算子是一个具有滤波，增强，检测的多阶段的优化算子，在进行处理前，Canny算子先利用高斯平滑滤波器来平滑图像以除去噪声，Canny分割算法采用一阶偏导的有限差分来计算梯度幅值和方向，在处理过程中，Canny算子还将经过一个非极大值抑制的过程，最后Canny算子还采用两个阈值来连接边缘。
Canny边缘检测算法：
step1: 用高斯滤波器平滑图象；
step2: 用一阶偏导的有限差分来计算梯度的幅值和方向；
step3: 对梯度幅值进行非极大值抑制
step4: 用双阈值算法检测和连接边缘
拉普拉斯算子：
Laplace算子是一种各向同性算子，二阶微分算子。一个函数的一阶微分描述了函数图像是朝哪里变化的，即增长或者降低；而二阶微分描述的则是图像变化的速度，急剧增长下降还是平缓的增长下降。当邻域中心像素灰度低于它所在的领域内其它像素的平均灰度时，此中心像素的灰度应被进一步降低，当邻域中心像素灰度高于它所在的邻域内其它像素的平均灰度时，此中心像素的灰度应被进一步提高，以此实现图像的锐化处理。
算子定义为

下面由算子推导计算模板系数
在x方向上，二阶导数的微分可以由差分近似表示，有

类似地，在y方向上有

所以拉普拉斯算子在离散的情况下，可以近似为

还有一般常用的其他拉普拉斯模板

4.2.1.2 非线性滤波

非线性滤波: 输出的信号响应是由输入经过非线性的运算得到的。比如典型的中值滤波，就是取像素点邻域的中值作为像素的的响应输出。
非线性滤波包含:中值滤波，最大最小值滤波，双边滤波。
双边滤波：
一种同时考虑了像素空间差异与强度差异的滤波器，因此具有保持图像边缘的特性。先看看高斯滤波器

其中W是权重，i和j是像素索引，K是归一化常量。公式中可以看出，权重只和像素之间的空间距离有关系，无论图像的内容是什么，都有相同的滤波效果。
再来看看双边滤波器，它只是在原有高斯函数的基础上加了一项，如下

其中 I 是像素的强度值，所以在强度差距大的地方（边缘），权重会减小，滤波效应也就变小。总体而言，在像素强度变换不大的区域，双边滤波有类似于高斯滤波的效果，而在图像边缘等强度梯度较大的地方，可以保持梯度。

4.2.2 卷积滤波和相关滤波

首先要注意的是卷积滤波和相关滤波都属于线性滤波，两者的区别是加权系数的对应相乘顺序有所不同。相关是滤波器模板移过图像并计算计算每个位置乘积之和的处理，卷积的机理相似，但滤波器首先要旋转180度。

4.2.3 空间滤波和频域滤波

空间滤波即直接在像素坐标上对图像数据进行处理滤波，频域滤波则是先把图像由空间域变换到频域，在频域进行处理，结束以后再由频域变换会空间域。

有关频域滤波的只是参考：

1. 数字图像处理-频域滤波-高通/低通滤波
2. 数字图像处理-频域滤波-带通/带阻滤波
   周期性噪声很适合在频域中滤波进行处理。周期性的噪声有一定的变化频率，我们只需要设计一个滤波器，在频域空间将这个频率的信息消除就可以完成频域滤波，而不影响其他频率的信息。相比空间域滤波具有很大的优势。
   这篇博客图像的二维傅里叶变换频谱图特点研究挺有意思的,分析了简单模式的频谱情况。

参考文献：

1. 数字图像处理之几种滤波器
2. 图像处理中的滤波
3. [转]几种图像边缘检测算子的比较
4. 边缘检测算法及各自优缺点
5. 边缘检测算子总结
6. 图像与滤波