文章出处: http://blog.csdn.net/zajin/article/details/8556614
微软2013年经典的算法面试100题(第1-20题)
算法面试:精选微软经典的算法面试100题
引言:
给你10分钟时间,根据上排给出十个数,在其下排填出对应的十个数
要求下排每个数都是先前上排那十个数在下排出现的次数。
上排的十个数如下:
【0,1,2,3,4,5,6,7,8,9】
举一个例子,
数值:0,1,2,3,4,5,6,7,8,9
分配:6,2,1,0,0,0,1,0,0,0
0在下排出现了6次,1在下排出现了2次,
2在下排出现了1次,3在下排出现了0次....
以此类推..
算法面试:精选微软等公司经典的算法面试100题 第1-20题
如下:
--------------- --------------
1.把二元查找树转变成排序的双向链表
题目:
输入一棵二元查找树,将该二元查找树转换成一个排序的双向链表。
要求不能创建任何新的结点,只调整指针的指向。
10
/ /
6 14
/ / / /
4 8 12 16
转换成双向链表
4=6=8=10=12=14=16。
首先我们定义的二元查找树 节点的数据结构如下:
struct BSTreeNode
{
int m_nValue; // value of node
BSTreeNode *m_pLeft; // left child of node
BSTreeNode *m_pRight; // right child of node
};
2.设计包含min函数的栈。
定义栈的数据结构,要求添加一个min函数,能够得到栈的最小元素。
要求函数min、push以及pop的时间复杂度都是O(1)。
3.求子数组的最大和
题目:
输入一个整形数组,数组里有正数也有负数。
数组中连续的一个或多个整数组成一个子数组,每个子数组都有一个和。
求所有子数组的和的最大值。要求时间复杂度为O(n)。
例如输入的数组为1, -2, 3, 10, -4, 7, 2, -5,和最大的子数组为3, 10, -4, 7, 2,
因此输出为该子数组的和18。
4.在二元树中找出和为某一值的所有路径
题目:输入一个整数和一棵二元树。
从树的根结点开始往下访问一直到叶结点所经过的所有结点形成一条路径。
打印出和与输入整数相等的所有路径。
例如 输入整数22和如下二元树
10
/ /
5 12
/ /
4 7
则打印出两条路径:10, 12和10, 5, 7。
二元树节点的数据结构定义为:
struct BinaryTreeNode // a node in the binary tree
{
int m_nValue; // value of node
BinaryTreeNode *m_pLeft; // left child of node
BinaryTreeNode *m_pRight; // right child of node
};
5.查找最小的k个元素
题目:输入n个整数,输出其中最小的k个。
例如输入1,2,3,4,5,6,7和8这8个数字,则最小的4个数字为1,2,3和4。
第6题
腾讯面试题:
给你10分钟时间,根据上排给出十个数,在其下排填出对应的十个数
要求下排每个数都是先前上排那十个数在下排出现的次数。
上排的十个数如下:
【0,1,2,3,4,5,6,7,8,9】
初看此题,貌似很难,10分钟过去了,可能有的人,题目都还没看懂。
举一个例子,
数值: 0,1,2,3,4,5,6,7,8,9
分配: 6,2,1,0,0,0,1,0,0,0
0在下排出现了6次,1在下排出现了2次,
2在下排出现了1次,3在下排出现了0次....
以此类推..
昨天,花了一个下午,用c++实现了此题。(*^__^*)
第7题
微软亚院之编程判断俩个链表是否相交
给出俩个单向链表的头指针,比如h1,h2,判断这俩个链表是否相交。
为了简化问题,我们假设俩个链表均不带环。
问题扩展:
1.如果链表可能有环列?
2.如果需要求出俩个链表相交的第一个节点列?
第8题
此贴选一些 比较怪的题,,由于其中题目本身与算法关系不大,仅考考思维。特此并作一题。
1.有两个房间,一间房里有三盏灯,另一间房有控制着三盏灯的三个开关,这两个房间是 分割开的,从一间里不能看到另一间的情况。
现在要求受训者分别进这两房间一次,然后判断出这三盏灯分别是由哪个开关控制的。
有什么办法呢?
2.你让一些人为你工作了七天,你要用一根金条作为报酬。金条被分成七小块,每天给出一块。如果你只能将金条切割两次,你怎样分给这些工人?
3.★链接表和数组之间的区别是什么?
★做一个链接表,你为什么要选择这样的方法?
★选择一种算法来整理出一个链接表。你为什么要选择这种方法?现在用O(n)时间来做。
★说说各种股票分类算法的优点和缺点。
★用一种算法来颠倒一个链接表的顺序。现在在不用递归式的情况下做一遍。
★用一种算法在一个循环的链接表里插入一个节点,但不得穿越链接表。
★用一种算法整理一个数组。你为什么选择这种方法?
★用一种算法使通用字符串相匹配。
★颠倒一个字符串。优化速度。优化空间。
★颠倒一个句子中的词的顺序,比如将“我叫克丽丝”转换为“克丽丝叫我”,实现速度最快,移动最少。
★找到一个子字符串。优化速度。优化空间。
★比较两个字符串,用O(n)时间和恒量空间。
★假设你有一个用1001个整数组成的数组,这些整数是任意排列的,但是你知道所有的整数都在1到1000(包括1000)之间。此外,除一个数字出现两次外,其他所有数字只出现一次。假设你只能对这个数组做一次处理,用一种算法找出重复的那个数字。如果你在运算中使用了辅助的存储方式,那么你能找到不用这种方式的算法吗?
★不用乘法或加法增加8倍。现在用同样的方法增加7倍。
第9题
判断整数序列是不是二元查找树的后序遍历结果
题目:输入一个整数数组,判断该数组是不是某二元查找树的后序遍历的结果。
如果是返回true,否则返回false。
例如输入5、7、6、9、11、10、8,由于这一整数序列是如下树的后序遍历结果:
8
/ /
6 10
/ / / /
5 7 9 11
因此返回true。
如果输入7、4、6、5,没有哪棵树的后序遍历的结果是这个序列,因此返回false。
第10题
翻转句子中单词的顺序。
题目:输入一个英文句子,翻转句子中单词的顺序,但单词内字符的顺序不变。句子中单词以空格符隔开。
为简单起见,标点符号和普通字母一样处理。
例如输入“I am a student.”,则输出“student. a am I”。
第11题
求二叉树中节点的最大距离...
如果我们把二叉树看成一个图,
父子节点之间的连线看成是双向的,
我们姑且定义"距离"为两节点之间边的个数。
写一个程序,
求一棵二叉树中相距最远的两个节点之间的距离。
第12题
题目:求1+2+…+n,
要求不能使用乘除法、for、while、if、else、switch、case等关键字以及条件判断语句(A?B:C)。
第13题:
题目:输入一个单向链表,输出该链表中倒数第k个结点。链表的倒数第0个结点为链表的尾指针。
链表结点定义如下:
struct ListNode
{
int m_nKey;
ListNode* m_pNext;
};
第14题:
题目:输入一个已经按升序排序过的数组和一个数字,
在数组中查找两个数,使得它们的和正好是输入的那个数字。
要求时间复杂度是O(n)。如果有多对数字的和等于输入的数字,输出任意一对即可。
例如输入数组1、2、4、7、11、15和数字15。由于4+11=15,因此输出4和11。
第15题:
题目:输入一颗二元查找树,将该树转换为它的镜像,
即在转换后的二元查找树中,左子树的结点都大于右子树的结点。
用递归和循环两种方法完成树的镜像转换。
例如输入:
8
/ /
6 10
// //
5 7 9 11
输出:
8
/ /
10 6
// //
11 9 7 5
定义二元查找树的结点为:
struct BSTreeNode // a node in the binary search tree (BST)
{
int m_nValue; // value of node
BSTreeNode *m_pLeft; // left child of node
BSTreeNode *m_pRight; // right child of node
};
第16题:
题目(微软):
输入一颗二元树,从上往下按层打印树的每个结点,同一层中按照从左往右的顺序打印。
例如输入
8
/ /
6 10
/ / / /
5 7 9 11
输出8 6 10 5 7 9 11。
第17题:
题目:在一个字符串中找到第一个只出现一次的字符。如输入abaccdeff,则输出b。
分析:这道题是2006年google的一道笔试题。
第18题:
题目:n个数字(0,1,…,n-1)形成一个圆圈,从数字0开始,
每次从这个圆圈中删除第m个数字(第一个为当前数字本身,第二个为当前数字的下一个数字)。
当一个数字删除后,从被删除数字的下一个继续删除第m个数字。
求出在这个圆圈中剩下的最后一个数字。
July:我想,这个题目,不少人已经 见识过了。
第19题:
题目:定义Fibonacci数列如下:
/ 0 n=0
f(n)= 1 n=1
/ f(n-1)+f(n-2) n=2
输入n,用最快的方法求该数列的第n项。
分析:在很多C语言教科书中讲到递归函数的时候,都会用Fibonacci作为例子。
因此很多程序员对这道题的递归解法非常熟悉,但....呵呵,你知道的。。
第20题:
题目:输入一个表示整数的字符串,把该字符串转换成整数并输出。
例如输入字符串"345",则输出整数345。
微软2013年经典的算法面试100题(第21-25题)
算法面试:精选微软等公司经典的算法面试100题 第21-25题
---------------------------------
2010年10月15日
第21题
2010年中兴面试题
编程求解:
输入两个整数 n 和 m,从数列1,2,3.......n 中 随意取几个数,
使其和等于 m ,要求将其中所有的可能组合列出来.
第22题:
有4张红色的牌和4张蓝色的牌,主持人先拿任意两张,再分别在A、B、C三人额头上贴任意两张牌,
A、B、C三人都可以看见其余两人额头上的牌,看完后让他们猜自己额头上是什么颜色的牌,
A说不知道,B说不知道,C说不知道,然后A说知道了。
请教如何推理,A是怎么知道的。
如果用程序,又怎么实现呢?
第23题:
用最简单, 最快速的方法计算出下面这个圆形是否和正方形相交。"
3D坐标系 原点(0.0,0.0,0.0)
圆形:
半径r = 3.0
圆心o = (*.*, 0.0, *.*)
正方形:
4个角坐标;
1:(*.*, 0.0, *.*)
2:(*.*, 0.0, *.*)
3:(*.*, 0.0, *.*)
4:(*.*, 0.0, *.*)
第24题:
链表操作,
(1).单链表就地逆置,
(2)合并链表
第25题:
写一个函数,它的原形是int continumax(char *outputstr,char *intputstr)
功能:
在字符串中找出连续最长的数字串,并把这个串的长度返回,
并把这个最长数字串付给其中一个函数参数outputstr所指内存。
例如:"abcd12345ed125ss123456789"的首地址传给intputstr后,函数将返回9,
outputstr所指的值为123456789
微软等公司2013年经典的算法面试100题 第26-35题
算法面试:精选微软等公司经典的算法面试100题 第26-35题
26.左旋转字符串
题目:
定义字符串的左旋转操作:把字符串前面的若干个字符移动到字符串的尾部。
如把字符串abcdef左旋转2位得到字符串cdefab。请实现字符串左旋转的函数。
要求时间对长度为n的字符串操作的复杂度为O(n),辅助内存为O(1)。
27.跳台阶问题
题目:一个台阶总共有n级,如果一次可以跳1级,也可以跳2级。
求总共有多少总跳法,并分析算法的时间复杂度。
这道题最近经常出现,包括MicroStrategy等比较重视算法的公司都
曾先后选用过个这道题作为面试题或者笔试题。
28.整数的二进制表示中1的个数
题目:输入一个整数,求该整数的二进制表达中有多少个1。
例如输入10,由于其二进制表示为1010,有两个1,因此输出2。
分析:
这是一道很基本的考查位运算的面试题。
包括微软在内的很多公司都曾采用过这道题。
29.栈的push、pop序列
题目:输入两个整数序列。其中一个序列表示栈的push顺序,
判断另一个序列有没有可能是对应的pop顺序。
为了简单起见,我们假设push序列的任意两个整数都是不相等的。
比如输入的push序列是1、2、3、4、5,那么4、5、3、2、1就有可能是一个pop系列。
因为可以有如下的push和pop序列:
push 1,push 2,push 3,push 4,pop,push 5,pop,pop,pop,pop,
这样得到的pop序列就是4、5、3、2、1。
但序列4、3、5、1、2就不可能是push序列1、2、3、4、5的pop序列。
30.在从1到n的正数中1出现的次数
题目:输入一个整数n,求从1到n这n个整数的十进制表示中1出现的次数。
例如输入12,从1到12这些整数中包含1 的数字有1,10,11和12,1一共出现了5次。
分析:这是一道广为流传的google面试题。
31.华为面试题:
一类似于蜂窝的结构的图,进行搜索最短路径(要求5分钟)
32.
有两个序列a,b,大小都为n,序列元素的值任意整数,无序;
要求:通过交换a,b中的元素,使[序列a元素的和]与[序列b元素的和]之间的差最小。
例如:
var a=[100,99,98,1,2, 3];
var b=[1, 2, 3, 4,5,40];
33.
实现一个挺高级的字符匹配算法:
给一串很长字符串,要求找到符合要求的字符串,例如目的串:123
1******3***2 ,12*****3这些都要找出来
其实就是类似一些和谐系统。。。。。
34.
实现一个队列。
队列的应用场景为:
一个生产者线程将int类型的数入列,一个消费者线程将int类型的数出列
35.
求一个矩阵中最大的二维矩阵(元素和最大).如:
1 2 0 3 4
2 3 4 5 1
1 1 5 3 0
中最大的是:
4 5
5 3
要求:(1)写出算法;(2)分析时间复杂度;(3)用C写出关键代码
精选微软等公司数据结构+算法面试100题 [第1-40题]
精选微软等公司,数据结构+算法,经典面试100题
--------之前40题
--------------- --------------
1.把二元查找树转变成排序的双向链表
题目:
输入一棵二元查找树,将该二元查找树转换成一个排序的双向链表。
要求不能创建任何新的结点,只调整指针的指向。
10
/ /
6 14
/ / / /
4 8 12 16
转换成双向链表
4=6=8=10=12=14=16。
首先我们定义的二元查找树 节点的数据结构如下:
struct BSTreeNode
{
int m_nValue; // value of node
BSTreeNode *m_pLeft; // left child of node
BSTreeNode *m_pRight; // right child of node
};
2.设计包含min函数的栈。
定义栈的数据结构,要求添加一个min函数,能够得到栈的最小元素。
要求函数min、push以及pop的时间复杂度都是O(1)。
3.求子数组的最大和
题目:
输入一个整形数组,数组里有正数也有负数。
数组中连续的一个或多个整数组成一个子数组,每个子数组都有一个和。
求所有子数组的和的最大值。要求时间复杂度为O(n)。
例如输入的数组为1, -2, 3, 10, -4, 7, 2, -5,和最大的子数组为3, 10, -4, 7, 2,
因此输出为该子数组的和18。
4.在二元树中找出和为某一值的所有路径
题目:输入一个整数和一棵二元树。
从树的根结点开始往下访问一直到叶结点所经过的所有结点形成一条路径。
打印出和与输入整数相等的所有路径。
例如 输入整数22和如下二元树
10
/ /
5 12
/ /
4 7
则打印出两条路径:10, 12和10, 5, 7。
二元树节点的数据结构定义为:
struct BinaryTreeNode // a node in the binary tree
{
int m_nValue; // value of node
BinaryTreeNode *m_pLeft; // left child of node
BinaryTreeNode *m_pRight; // right child of node
};
5.查找最小的k个元素
题目:输入n个整数,输出其中最小的k个。
例如输入1,2,3,4,5,6,7和8这8个数字,则最小的4个数字为1,2,3和4。
第6题
------------------------------------
腾讯面试题:
给你10分钟时间,根据上排给出十个数,在其下排填出对应的十个数
要求下排每个数都是先前上排那十个数在下排出现的次数。
上排的十个数如下:
【0,1,2,3,4,5,6,7,8,9】
初看此题,貌似很难,10分钟过去了,可能有的人,题目都还没看懂。
举一个例子,
数值: 0,1,2,3,4,5,6,7,8,9
分配: 6,2,1,0,0,0,1,0,0,0
0在下排出现了6次,1在下排出现了2次,
2在下排出现了1次,3在下排出现了0次....
以此类推..
第7题
------------------------------------
微软亚院之编程判断俩个链表是否相交
给出俩个单向链表的头指针,比如h1,h2,判断这俩个链表是否相交。
为了简化问题,我们假设俩个链表均不带环。
问题扩展:
1.如果链表可能有环列?
2.如果需要求出俩个链表相交的第一个节点列?
第8题
------------------------------------
此贴选一些 比较怪的题,,由于其中题目本身与算法关系不大,仅考考思维。特此并作一题。
1.有两个房间,一间房里有三盏灯,另一间房有控制着三盏灯的三个开关,这两个房间是 分割开的,
从一间里不能看到另一间的情况。
现在要求受训者分别进这两房间一次,然后判断出这三盏灯分别是由哪个开关控制的。
有什么办法呢?
2.你让一些人为你工作了七天,你要用一根金条作为报酬。金条被分成七小块,每天给出一块。
如果你只能将金条切割两次,你怎样分给这些工人?
3 ★用一种算法来颠倒一个链接表的顺序。现在在不用递归式的情况下做一遍。
★用一种算法在一个循环的链接表里插入一个节点,但不得穿越链接表。
★用一种算法整理一个数组。你为什么选择这种方法?
★用一种算法使通用字符串相匹配。
★颠倒一个字符串。优化速度。优化空间。
★颠倒一个句子中的词的顺序,比如将“我叫克丽丝”转换为“克丽丝叫我”,实现速度最快,移动最少。
★找到一个子字符串。优化速度。优化空间。
★比较两个字符串,用O(n)时间和恒量空间。
★假设你有一个用1001个整数组成的数组,这些整数是任意排列的,但是你知道所有的整数都在1到1000(包括1000)之间。此外,除一个数字出现两次外,其他所有数字只出现一次
。假设你只能对这个数组做一次处理,用一种算法找出重复的那个数字。
如果你在运算中使用了辅助的存储方式,那么你能找到不用这种方式的算法吗?
★不用乘法或加法增加8倍。现在用同样的方法增加7倍。
第9题
-----------------------------------
判断整数序列是不是二元查找树的后序遍历结果
题目:输入一个整数数组,判断该数组是不是某二元查找树的后序遍历的结果。
如果是返回true,否则返回false。
例如输入5、7、6、9、11、10、8,由于这一整数序列是如下树的后序遍历结果:
8
/ /
6 10
/ / / /
5 7 9 11
因此返回true。
如果输入7、4、6、5,没有哪棵树的后序遍历的结果是这个序列,因此返回false。
第10题
---------------------------------
翻转句子中单词的顺序。
题目:输入一个英文句子,翻转句子中单词的顺序,但单词内字符的顺序不变。句子中单词以空格符隔开。
为简单起见,标点符号和普通字母一样处理。
例如输入“I am a student.”,则输出“student. a am I”。
第11题
------------------------------------
求二叉树中节点的最大距离...
如果我们把二叉树看成一个图,
父子节点之间的连线看成是双向的,
我们姑且定义"距离"为两节点之间边的个数。
写一个程序,
求一棵二叉树中相距最远的两个节点之间的距离。
第12题
题目:求1+2+…+n,
要求不能使用乘除法、for、while、if、else、switch、case等关键字以及条件判断语句(A?B:C)。
第13题:
题目:输入一个单向链表,输出该链表中倒数第k个结点。链表的倒数第0个结点为链表的尾指针。
链表结点定义如下:
struct ListNode
{
int m_nKey;
ListNode* m_pNext;
};
第14题:
题目:输入一个已经按升序排序过的数组和一个数字,
在数组中查找两个数,使得它们的和正好是输入的那个数字。
要求时间复杂度是O(n)。如果有多对数字的和等于输入的数字,输出任意一对即可。
例如输入数组1、2、4、7、11、15和数字15。由于4+11=15,因此输出4和11。
第15题:
题目:输入一颗二元查找树,将该树转换为它的镜像,
即在转换后的二元查找树中,左子树的结点都大于右子树的结点。
用递归和循环两种方法完成树的镜像转换。
例如输入:
8
/ /
6 10
// //
5 7 9 11
输出:
8
/ /
10 6
// //
11 9 7 5
定义二元查找树的结点为:
struct BSTreeNode // a node in the binary search tree (BST)
{
int m_nValue; // value of node
BSTreeNode *m_pLeft; // left child of node
BSTreeNode *m_pRight; // right child of node
};
第16题:
题目(微软):
输入一颗二元树,从上往下按层打印树的每个结点,同一层中按照从左往右的顺序打印。
例如输入
8
/ /
6 10
/ / / /
5 7 9 11
输出8 6 10 5 7 9 11。
第17题:
题目:在一个字符串中找到第一个只出现一次的字符。如输入abaccdeff,则输出b。
分析:这道题是2006年google的一道笔试题。
第18题:
题目:n个数字(0,1,…,n-1)形成一个圆圈,从数字0开始,
每次从这个圆圈中删除第m个数字(第一个为当前数字本身,第二个为当前数字的下一个数字)。
当一个数字删除后,从被删除数字的下一个继续删除第m个数字。
求出在这个圆圈中剩下的最后一个数字。
July:我想,这个题目,不少人已经 见识过了。
第19题:
题目:定义Fibonacci数列如下:
/ 0 n=0
f(n)= 1 n=1
/ f(n-1)+f(n-2) n=2
输入n,用最快的方法求该数列的第n项。
分析:在很多C语言教科书中讲到递归函数的时候,都会用Fibonacci作为例子。
因此很多程序员对这道题的递归解法非常熟悉,但....呵呵,你知道的。。
第20题:
题目:输入一个表示整数的字符串,把该字符串转换成整数并输出。
例如输入字符串"345",则输出整数345。
第21题
2010年中兴面试题
编程求解:
输入两个整数 n 和 m,从数列1,2,3.......n 中 随意取几个数,
使其和等于 m ,要求将其中所有的可能组合列出来.
第22题:
有4张红色的牌和4张蓝色的牌,主持人先拿任意两张,再分别在A、B、C三人额头上贴任意两张牌,
A、B、C三人都可以看见其余两人额头上的牌,看完后让他们猜自己额头上是什么颜色的牌,
A说不知道,B说不知道,C说不知道,然后A说知道了。
请教如何推理,A是怎么知道的。
如果用程序,又怎么实现呢?
第23题:
用最简单, 最快速的方法计算出下面这个圆形是否和正方形相交。"
3D坐标系 原点(0.0,0.0,0.0)
圆形:
半径r = 3.0
圆心o = (*.*, 0.0, *.*)
正方形:
4个角坐标;
1:(*.*, 0.0, *.*)
2:(*.*, 0.0, *.*)
3:(*.*, 0.0, *.*)
4:(*.*, 0.0, *.*)
第24题:
链表操作,
(1).单链表就地逆置,
(2)合并链表
第25题:
写一个函数,它的原形是int continumax(char *outputstr,char *intputstr)
功能:
在字符串中找出连续最长的数字串,并把这个串的长度返回,
并把这个最长数字串付给其中一个函数参数outputstr所指内存。
例如:"abcd12345ed125ss123456789"的首地址传给intputstr后,函数将返回9,
outputstr所指的值为123456789
26.左旋转字符串
题目:
定义字符串的左旋转操作:把字符串前面的若干个字符移动到字符串的尾部。
如把字符串abcdef左旋转2位得到字符串cdefab。请实现字符串左旋转的函数。
要求时间对长度为n的字符串操作的复杂度为O(n),辅助内存为O(1)。
27.跳台阶问题
题目:一个台阶总共有n级,如果一次可以跳1级,也可以跳2级。
求总共有多少总跳法,并分析算法的时间复杂度。
这道题最近经常出现,包括MicroStrategy等比较重视算法的公司都
曾先后选用过个这道题作为面试题或者笔试题。
28.整数的二进制表示中1的个数
题目:输入一个整数,求该整数的二进制表达中有多少个1。
例如输入10,由于其二进制表示为1010,有两个1,因此输出2。
分析:
这是一道很基本的考查位运算的面试题。
包括微软在内的很多公司都曾采用过这道题。
29.栈的push、pop序列
题目:输入两个整数序列。其中一个序列表示栈的push顺序,
判断另一个序列有没有可能是对应的pop顺序。
为了简单起见,我们假设push序列的任意两个整数都是不相等的。
比如输入的push序列是1、2、3、4、5,那么4、5、3、2、1就有可能是一个pop系列。
因为可以有如下的push和pop序列:
push 1,push 2,push 3,push 4,pop,push 5,pop,pop,pop,pop,
这样得到的pop序列就是4、5、3、2、1。
但序列4、3、5、1、2就不可能是push序列1、2、3、4、5的pop序列。
30.在从1到n的正数中1出现的次数
题目:输入一个整数n,求从1到n这n个整数的十进制表示中1出现的次数。
例如输入12,从1到12这些整数中包含1 的数字有1,10,11和12,1一共出现了5次。
分析:这是一道广为流传的google面试题。
31.华为面试题:
一类似于蜂窝的结构的图,进行搜索最短路径(要求5分钟)
32.
有两个序列a,b,大小都为n,序列元素的值任意整数,无序;
要求:通过交换a,b中的元素,使[序列a元素的和]与[序列b元素的和]之间的差最小。
例如:
var a=[100,99,98,1,2, 3];
var b=[1, 2, 3, 4,5,40];
33.
实现一个挺高级的字符匹配算法:
给一串很长字符串,要求找到符合要求的字符串,例如目的串:123
1******3***2 ,12*****3这些都要找出来
其实就是类似一些和谐系统。。。。。
34.
实现一个队列。
队列的应用场景为:
一个生产者线程将int类型的数入列,一个消费者线程将int类型的数出列
35.
求一个矩阵中最大的二维矩阵(元素和最大).如:
1 2 0 3 4
2 3 4 5 1
1 1 5 3 0
中最大的是:
4 5
5 3
要求:(1)写出算法;(2)分析时间复杂度;(3)用C写出关键代码
第36题-40题(有些题目搜集于CSDN上的网友,已标明):
36.引用自网友:longzuo
谷歌笔试:
n支队伍比赛,分别编号为0,1,2。。。。n-1,已知它们之间的实力对比关系,
存储在一个二维数组w[n][n]中,w[i][j] 的值代表编号为i,j的队伍中更强的一支。
所以w[i][j]=i 或者j,现在给出它们的出场顺序,并存储在数组order[n]中,
比如order[n] = {4,3,5,8,1......},那么第一轮比赛就是 4对3, 5对8。.......
胜者晋级,败者淘汰,同一轮淘汰的所有队伍排名不再细分,即可以随便排,
下一轮由上一轮的胜者按照顺序,再依次两两比,比如可能是4对5,直至出现第一名
编程实现,给出二维数组w,一维数组order 和 用于输出比赛名次的数组result[n],求出result。
37.
有n个长为m+1的字符串,
如果某个字符串的最后m个字符与某个字符串的前m个字符匹配,则两个字符串可以联接,
问这n个字符串最多可以连成一个多长的字符串,如果出现循环,则返回错误。
38.
百度面试:
1.用天平(只能比较,不能称重)从一堆小球中找出其中唯一一个较轻的,使用x次天平,最多可以从y个小球中找出较轻的那个,求y与x的关系式
2.有一个很大很大的输入流,大到没有存储器可以将其存储下来,而且只输入一次,如何从这个输入流中随机取得m个记录
3.大量的URL字符串,如何从中去除重复的,优化时间空间复杂度
39.
网易有道笔试:
(1).
求一个二叉树中任意两个节点间的最大距离,
两个节点的距离的定义是 这两个节点间边的个数,
比如某个孩子节点和父节点间的距离是1,和相邻兄弟节点间的距离是2,优化时间空间复杂度。
(2).
求一个有向连通图的割点,割点的定义是,如果除去此节点和与其相关的边,
有向图不再连通,描述算法。
40.百度研发笔试题
引用自:zp155334877
1)设计一个栈结构,满足一下条件:min,push,pop操作的时间复杂度为O(1)。
2)一串首尾相连的珠子(m个),有N种颜色(N<=10),
设计一个算法,取出其中一段,要求包含所有N中颜色,并使长度最短。
并分析时间复杂度与空间复杂度。
3)设计一个系统处理词语搭配问题,比如说 中国 和人民可以搭配,
则中国人民 人民中国都有效。要求:
*系统每秒的查询数量可能上千次;
*词语的数量级为10W;
*每个词至多可以与1W个词搭配
当用户输入中国人民的时候,要求返回与这个搭配词组相关的信息。
作者声明:
1.由于其中大部题目搜集于网络。有的流传甚广,个别题,我已无法考究,究竟最初源自哪里。
但,所有资料如此精选整理,的确是出自于我手。且题目的答案由我个人和一些网友完成。
如此,我自称为作者,我想并不过分。
2.作者本人July对以上所有任何资料享有版权。转载请注明出处。谢谢。July。
精选微软等公司数据结构+算法面试100题 [第41-60题]
精选微软等公司数据结构+算法,经典面试100题 [第1题-第60题]
-------- 首次公布
July声明:首次发布。请尊重作者。
20:38:53 2010-10-29
----------------------------------------------------
前40题:
[整理I]精选微软等公司数据结构+算法面试100题 [第1-40题]
http://blog.csdn.net/v_JULY_v/archive/2010/10/27/5968678.aspx
41.求固晶机的晶元查找程序
晶元盘由数目不详的大小一样的晶元组成,晶元并不一定全布满晶元盘,
照相机每次这能匹配一个晶元,如匹配过,则拾取该晶元,
若匹配不过,照相机则按测好的晶元间距移到下一个位置。
求遍历晶元盘的算法 求思路。
42.请修改append函数,利用这个函数实现:
两个非降序链表的并集,1->2->3 和 2->3->5 并为 1->2->3->5
另外只能输出结果,不能修改两个链表的数据。
43.递归和非递归俩种方法实现二叉树的前序遍历。
44.腾讯面试题:
1.设计一个魔方(六面)的程序。
2.有一千万条短信,有重复,以文本文件的形式保存,一行一条,有重复。
请用5分钟时间,找出重复出现最多的前10条。
3.收藏了1万条url,现在给你一条url,如何找出相似的url。(面试官不解释何为相似)
45.雅虎:
1.对于一个整数矩阵,存在一种运算,对矩阵中任意元素加一时,需要其相邻(上下左右)某一个元素也加一,
现给出一正数矩阵,判断其是否能够由一个全零矩阵经过上述运算得到。
2.一个整数数组,长度为n,将其分为m份,使各份的和相等,求m的最大值
比如{3,2,4,3,6} 可以分成{3,2,4,3,6} m=1;
{3,6}{2,4,3} m=2
{3,3}{2,4}{6} m=3 所以m的最大值为3
46.搜狐:
四对括号可以有多少种匹配排列方式?比如两对括号可以有两种:()()和(())
47.创新工场:
求一个数组的最长递减子序列 比如{9,4,3,2,5,4,3,2}的最长递减子序列为{9,5,4,3,2}
48.微软:
一个数组是由一个递减数列左移若干位形成的,比如{4,3,2,1,6,5}
是由{6,5,4,3,2,1}左移两位形成的,在这种数组中查找某一个数。
49.一道看上去很吓人的算法面试题:
如何对n个数进行排序,要求时间复杂度O(n),空间复杂度O(1)
50.网易有道笔试:
1.求一个二叉树中任意两个节点间的最大距离,两个节点的距离的定义是 这两个节点间边的个数,
比如某个孩子节点和父节点间的距离是1,和相邻兄弟节点间的距离是2,优化时间空间复杂度。
2.求一个有向连通图的割点,割点的定义是,
如果除去此节点和与其相关的边,有向图不再连通,描述算法。
51.和为n连续正数序列。
题目:输入一个正数n,输出所有和为n连续正数序列。
例如输入15,由于1+2+3+4+5=4+5+6=7+8=15,所以输出3个连续序列1-5、4-6和7-8。
分析:这是网易的一道面试题。
52.二元树的深度。
题目:输入一棵二元树的根结点,求该树的深度。
从根结点到叶结点依次经过的结点(含根、叶结点)形成树的一条路径,最长路径的长度为树的深度。
例如:输入二元树:
10
/ /
6 14
/ / /
4 12 16
输出该树的深度3。
二元树的结点定义如下:
struct SBinaryTreeNode // a node of the binary tree
{
int m_nValue; // value of node
SBinaryTreeNode *m_pLeft; // left child of node
SBinaryTreeNode *m_pRight; // right child of node
};
分析:这道题本质上还是考查二元树的遍历。
53.字符串的排列。
题目:输入一个字符串,打印出该字符串中字符的所有排列。
例如输入字符串abc,则输出由字符a、b、c所能排列出来的所有字符串abc、acb、bac、bca、cab和cba。
分析:这是一道很好的考查对递归理解的编程题,
因此在过去一年中频繁出现在各大公司的面试、笔试题中。
54.调整数组顺序使奇数位于偶数前面。
题目:输入一个整数数组,调整数组中数字的顺序,使得所有奇数位于数组的前半部分,
所有偶数位于数组的后半部分。要求时间复杂度为O(n)。
55.
题目:类CMyString的声明如下:
class CMyString
{
public:
CMyString(char* pData = NULL);
CMyString(const CMyString& str);
~CMyString(void);
CMyString& operator = (const CMyString& str);
private:
char* m_pData;
};
请实现其赋值运算符的重载函数,要求异常安全,即当对一个对象进行赋值时发生异常,对象的状态不能改变。
56.最长公共字串。
题目:如果字符串一的所有字符按其在字符串中的顺序出现在另外一个字符串二中,
则字符串一称之为字符串二的子串。
注意,并不要求子串(字符串一)的字符必须连续出现在字符串二中。
请编写一个函数,输入两个字符串,求它们的最长公共子串,并打印出最长公共子串。
例如:输入两个字符串BDCABA和ABCBDAB,字符串BCBA和BDAB都是是它们的最长公共子串,
则输出它们的长度4,并打印任意一个子串。
分析:求最长公共子串(Longest Common Subsequence, LCS)是一道非常经典的动态规划题,
因此一些重视算法的公司像MicroStrategy都把它当作面试题。
57.用俩个栈实现队列。
题目:某队列的声明如下:
template<typename T> class CQueue
{
public:
CQueue() {}
~CQueue() {}
void appendTail(const T& node); // append a element to tail
void deleteHead(); // remove a element from head
private:
T> m_stack1;
T> m_stack2;
};
分析:从上面的类的声明中,我们发现在队列中有两个栈。
因此这道题实质上是要求我们用两个栈来实现一个队列。
相信大家对栈和队列的基本性质都非常了解了:栈是一种后入先出的数据容器,
因此对队列进行的插入和删除操作都是在栈顶上进行;队列是一种先入先出的数据容器,
我们总是把新元素插入到队列的尾部,而从队列的头部删除元素。
58.从尾到头输出链表。
题目:输入一个链表的头结点,从尾到头反过来输出每个结点的值。链表结点定义如下:
struct ListNode
{
int m_nKey;
ListNode* m_pNext;
};
分析:这是一道很有意思的面试题。
该题以及它的变体经常出现在各大公司的面试、笔试题中。
59.不能被继承的类。
题目:用C++设计一个不能被继承的类。
分析:这是Adobe公司2007年校园招聘的最新笔试题。
这道题除了考察应聘者的C++基本功底外,还能考察反应能力,是一道很好的题目。
60.在O(1)时间内删除链表结点。
题目:给定链表的头指针和一个结点指针,在O(1)时间删除该结点。链表结点的定义如下:
struct ListNode
{
int m_nKey;
ListNode* m_pNext;
};
函数的声明如下:
void DeleteNode(ListNode* pListHead, ListNode* pToBeDeleted);
分析:这是一道广为流传的Google面试题,能有效考察我们的编程基本功,还能考察我们的反应速度,更重要的是,还能考察我们对时间复杂度的理解。
作者声明:
1.由于其中有些题目搜集于网络。有的流传甚广,个别题,我也无法考究究竟最初源自哪里。
但,所有资料如此精选整理,的确是出自于我手。且题目的答案由我个人和一些网友完成。
如此,我自称为作者,我想并不过分。
2.作者本人July对以上所有任何资料享有版权。转载请注明出处。谢谢。July。
[答案V0.1版]精选微软等数据结构+算法面试100题 [前20题]
精选微软等数据结构+算法面试100题
-------
我很享受思考的过程,个人思考的全部结果,都放在了这篇帖子上,
现在,我要,好好整理下,这篇帖子我已做出来的题目答案 了。
展示自己的思考结果,我觉得很骄傲。:)。
----------------------------------------------------------
2010年 10月18日下午 July
--------------------------------
1.把二元查找树转变成排序的双向链表
题目:
输入一棵二元查找树,将该二元查找树转换成一个排序的双向链表。
要求不能创建任何新的结点,只调整指针的指向。
10
/ /
6 14
/ / / /
4 8 12 16
转换成双向链表
4=6=8=10=12=14=16。
首先我们定义的二元查找树 节点的数据结构如下:
struct BSTreeNode
{
int m_nValue; // value of node
BSTreeNode *m_pLeft; // left child of node
BSTreeNode *m_pRight; // right child of node
};
//引用 245 楼 tree_star 的回复
#include <stdio.h>
#include <iostream.h>
struct BSTreeNode
{
int m_nValue; // value of node
BSTreeNode *m_pLeft; // left child of node
BSTreeNode *m_pRight; // right child of node
};
typedef struct BSTreeNode DoubleList;;DoubleList * pHead;
DoubleList * pListIndex;
void convertToDoubleList(BSTreeNode * pCurrent);
// 创建二元查找树
void addBSTreeNode(BSTreeNode * & pCurrent, int value)
{
if (NULL == pCurrent)
{
BSTreeNode * pBSTree = new BSTreeNode();
pBSTree -> m_pLeft = NULL;
pBSTree -> m_pRight = NULL;
pBSTree -> m_nValue = value;
pCurrent = pBSTree;
}
else
{
if ((pCurrent -> m_nValue) > value)
{
addBSTreeNode(pCurrent -> m_pLeft, value);
}
else if ((pCurrent -> m_nValue) < value)
{
addBSTreeNode(pCurrent -> m_pRight, value);
}
else
{
// cout<<"重复加入节点"<<endl;
}
}
}
// 遍历二元查找树 中序
void ergodicBSTree(BSTreeNode * pCurrent)
{
if (NULL == pCurrent)
{
return ;
}
if (NULL != pCurrent -> m_pLeft)
{
ergodicBSTree(pCurrent -> m_pLeft);
}
// 节点接到链表尾部
convertToDoubleList(pCurrent);
// 右子树为空
if (NULL != pCurrent -> m_pRight)
{
ergodicBSTree(pCurrent -> m_pRight);
}
}
// 二叉树转换成list
void convertToDoubleList(BSTreeNode * pCurrent)
{
pCurrent -> m_pLeft = pListIndex;
if (NULL != pListIndex)
{
pListIndex -> m_pRight = pCurrent;
}
else
{
pHead = pCurrent;
}
pListIndex = pCurrent;
cout << pCurrent -> m_nValue << endl;
}
int main()
{
BSTreeNode * pRoot = NULL;
pListIndex = NULL;
pHead = NULL;
addBSTreeNode(pRoot, 10 );
addBSTreeNode(pRoot, 4 );
addBSTreeNode(pRoot, 6 );
addBSTreeNode(pRoot, 8 );
addBSTreeNode(pRoot, 12 );
addBSTreeNode(pRoot, 14 );
addBSTreeNode(pRoot, 15 );
addBSTreeNode(pRoot, 16 );
ergodicBSTree(pRoot);
return 0 ;
}
/ //
4
6
8
10
12
14
15
16
Press any key to continue
/ /
2.设计包含min函数的栈。
定义栈的数据结构,要求添加一个min函数,能够得到栈的最小元素。
要求函数min、push以及pop的时间复杂度都是O(1)。
结合链表一起做。
首先我做插入以下数字:10,7,3,3,8,5,2, 6
0: 10 -> NULL (MIN=10, POS=0)
1: 7 -> [0] (MIN=7, POS=1) 用数组表示堆栈,第0个元素表示栈底
2: 3 -> [1] (MIN=3, POS=2)
3: 3 -> [2] (MIN=3, POS=3)
4: 8 -> NULL (MIN=3, POS=3) 技巧在这里,因为8比当前的MIN大,所以弹出8不会对当前的MIN产生影响
5:5 -> NULL (MIN=3, POS=3)
6: 2 -> [2] (MIN=2, POS=6) 如果2出栈了,那么3就是MIN
7: 6 -> [6]
出栈的话采用类似方法修正。
所以,此题的第1小题,即是借助辅助栈,保存最小值,
且随时更新辅助栈中的元素。
如先后,push 2 6 4 1 5
stack A stack B(辅助栈)
4: 5 1 //push 5,min=p->[3]=1 ^
3: 1 1 //push 1,min=p->[3]=1 | //此刻push进A的元素1小于B中栈顶元素2
2: 4 2 //push 4,min=p->[0]=2 |
1: 6 2 //push 6,min=p->[0]=2 |
0: 2 2 //push 2,min=p->[0]=2 |
push第一个元素进A,也把它push进B,
当向Apush的元素比B中的元素小, 则也push进B,即更新B。否则,不动B,保存原值。
向栈A push元素时,顺序由下至上。
辅助栈B中,始终保存着最小的元素。
然后,pop栈A中元素,5 1 4 6 2
A B ->更新
4: 5 1 1 //pop 5,min=p->[3]=1 |
3: 1 1 2 //pop 1,min=p->[0]=2 |
2: 4 2 2 //pop 4,min=p->[0]=2 |
1: 6 2 2 //pop 6,min=p->[0]=2 |
0: 2 2 NULL //pop 2,min=NULL v
当pop A中的元素小于B中栈顶元素时,则也要pop B中栈顶元素。
3.求子数组的最大和
题目:
输入一个整形数组,数组里有正数也有负数。
数组中连续的一个或多个整数组成一个子数组,每个子数组都有一个和。
求所有子数组的和的最大值。要求时间复杂度为O(n)。
例如输入的数组为1, -2, 3, 10, -4, 7, 2, -5,和最大的子数组为3, 10, -4, 7, 2,
因此输出为该子数组的和18。
//July 2010/10/18
#include <iostream.h>
int maxSum(int* a, int n)
{
int sum=0;
int b=0;
for(int i=0; i<n; i++)
{
if(b<0)
b=a[i];
else
b+=a[i];
if(sum<b)
sum=b;
}
return sum;
}
int main()
{
int a[10]={1,-8,6,3,-1,5,7,-2,0,1};
cout<<maxSum(a,10)<<endl;
return 0;
}
运行结果,如下:
20
Press any key to continue------------------------------------------------------------
int maxSum(int* a, int n)
{
int sum=0;
int b=0;
for(int i=0; i<n; i++)
{
if(b<=0) //此处修正下,把b<0改为 b<=0
b=a[i];
else
b+=a[i];
if(sum<b)
sum=b;
}
return sum;
}
//
解释下:
例如输入的数组为1, -2, 3, 10, -4, 7, 2, -5,
那么最大的子数组为3, 10, -4, 7, 2,
因此输出为该子数组的和18
所有的东西都在以下俩行,
即:
b:0 1 -1 3 13 9 16 18 7
sum:0 1 1 3 13 13 16 18 18
其实算法很简单,当前面的几个数,加起来后,b<0后,
把b重新赋值,置为下一个元素,b=a[i]。
当b>sum,则更新sum=b;
若b<sum,则sum保持原值,不更新。:)。July、10/31。
///
//关于第4题,
当访问到某一结点时,把该结点添加到路径上,并累加当前结点的值。
如果当前结点为叶结点并且当前路径的和刚好等于输入的整数,则当前的路径符合要求,我们把它打印出来。
如果当前结点不是叶结点,则继续访问它的子结点。当前结点访问结束后,递归函数将自动回到父结点。
因此我们在函数退出之前要在路径上删除当前结点并减去当前结点的值,
以确保返回父结点时路径刚好是根结点到父结点的路径。
我们不难看出保存路径的数据结构实际上是一个栈结构,因为路径要与递归调用状态一致,
而递归调用本质就是一个压栈和出栈的过程。
其中,部分题目源码及思路,参考自:
http://zhedahht.blog.163.com/blog/#m=0
void FindPath
(
BinaryTreeNode * pTreeNode, // a node of binary tree
int expectedSum, // the expected sum
std::vector < int >& path, // a path from root to current node
int & currentSum // the sum of path
)
{
if ( ! pTreeNode)
return ;
currentSum += pTreeNode -> m_nValue;
path.push_back(pTreeNode -> m_nValue);
// if the node is a leaf, and the sum is same as pre-defined,
// the path is what we want. print the path
bool isLeaf = ( ! pTreeNode -> m_pLeft && ! pTreeNode -> m_pRight);
if (currentSum == expectedSum && isLeaf)
{
std::vector < int > ::iterator iter = path.begin();
for (; iter != path.end(); ++ iter)
std::cout << * iter << ' /t ' ;
std::cout << std::endl;
}
// if the node is not a leaf, goto its children
if (pTreeNode -> m_pLeft)
FindPath(pTreeNode -> m_pLeft, expectedSum, path, currentSum);
if (pTreeNode -> m_pRight)
FindPath(pTreeNode -> m_pRight, expectedSum, path, currentSum);
// when we finish visiting a node and return to its parent node,
// we should delete this node from the path and
// minus the node's value from the current sum
currentSum -= pTreeNode -> m_nValue;
path.pop_back();
}
5.查找最小的k个元素
题目:输入n个整数,输出其中最小的k个。
例如输入1,2,3,4,5,6,7和8这8个数字,
则最小的4个数字为1,2,3和4。
//July 2010/10/18
//引用自116 楼 wocaoqwer 的回复。
#include<iostream>
using namespace std;
class MinK{
public:
MinK(int *arr,int si):array(arr),size(si){}
bool kmin(int k,int*& ret){
if(k>size)
{
ret=NULL;
return false;
}
else
{
ret=new int[k--];
int i;
for(i=0;i<=k;++i)
ret[i]=array[i];
for(int j=(k-1)/2;j>=0;--j)
shiftDown(ret,j,k);
for(;i<size;++i)
if(array[i]<ret[0])
{
ret[0]=array[i];
shiftDown(ret,0,k);
}
return true;
}
}
void remove(int*& ret){
delete[] ret;
ret=NULL;
}
private:
void shiftDown(int *ret,int pos,int length){
int t=ret[pos];
for(int s=2*pos+1;s<=length;s=2*s+1){
if(s<length&&ret[s]<ret[s+1])
++s;
if(t<ret[s])
{
ret[pos]=ret[s];
pos=s;
}
else break;
}
ret[pos]=t;
}
int *array;
int size;
};
int main()
{
int array[]={1,2,3,4,5,6,7,8};
MinK mink(array,sizeof(array)/sizeof(array[0]));
int *ret;
int k=4;
if(mink.kmin(k,ret))
{
for(int i=0;i<k;++i)
cout<<ret[i]<<endl;
mink.remove(ret);
}
return 0;
}
/////
运行结果:
4
2
3
1
Press any key to continue
/////
第6题
------------------------------------
腾讯面试题:
给你10分钟时间,根据上排给出十个数,在其下排填出对应的十个数
要求下排每个数都是先前上排那十个数在下排出现的次数。
上排的十个数如下:
【0,1,2,3,4,5,6,7,8,9】
初看此题,貌似很难,10分钟过去了,可能有的人,题目都还没看懂。
举一个例子,
数值: 0,1,2,3,4,5,6,7,8,9
分配: 6,2,1,0,0,0,1,0,0,0
0在下排出现了6次,1在下排出现了2次,
2在下排出现了1次,3在下排出现了0次....
以此类推..
// 引用自July 2010年10月18日。
//数值: 0,1,2,3,4,5,6,7,8,9
//分配: 6,2,1,0,0,0,1,0,0,0
#include <iostream.h>
#define len 10
class NumberTB
{
private:
int top[len];
int bottom[len];
bool success;
public:
NumberTB();
int* getBottom();
void setNextBottom();
int getFrequecy(int num);
};
NumberTB::NumberTB()
{
success = false;
//format top
for(int i=0;i<len;i++)
{
top[i] = i;
}
}
int* NumberTB::getBottom()
{
int i = 0;
while(!success)
{
i++;
setNextBottom();
}
return bottom;
}
//set next bottom
void NumberTB::setNextBottom()
{
bool reB = true;
for(int i=0;i<len;i++)
{
int frequecy = getFrequecy(i);
if(bottom[i] != frequecy)
{
bottom[i] = frequecy;
reB = false;
}
}
success = reB;
}
//get frequency in bottom
int NumberTB::getFrequecy(int num) //此处的num即指上排的数 i
{
int count = 0;
for(int i=0;i<len;i++)
{
if(bottom[i] == num)
count++;
}
return count; //cout即对应 frequecy
}
int main()
{
NumberTB nTB;
int* result= nTB.getBottom();
for(int i=0;i<len;i++)
{
cout<<*result++<<endl;
}
return 0;
}
///
运行结果:
6
2
1
0
0
0
1
0
0
0
Press any key to continue
/////
第7题
------------------------------------
微软亚院之编程判断俩个链表是否相交
给出俩个单向链表的头指针,比如h1,h2,判断这俩个链表是否相交。
为了简化问题,我们假设俩个链表均不带环。
问题扩展:
1.如果链表可能有环列?
2.如果需要求出俩个链表相交的第一个节点列?
//这一题,自己也和不少人讨论过了,
//更详细的,请看这里:
//My sina Blog:
//http://blog.sina.com.cn/s/blog_5e3ab00c0100le4s.html
1.首先假定链表不带环
那么,我们只要判断俩个链表的尾指针是否相等。
相等,则链表相交;否则,链表不相交。
2.如果链表带环,
那判断一链表上俩指针相遇的那个节点,在不在另一条链表上。
如果在,则相交,如果不在,则不相交。
所以,事实上,这个问题就转化成了:
1.先判断带不带环
2.如果都不带环,就判断尾节点是否相等
3.如果都带环,判断一链表上俩指针相遇的那个节点,在不在另一条链表上。
如果在,则相交,如果不在,则不相交。
//用两个指针,一个指针步长为1,一个指针步长为2,判断链表是否有环
bool check(const node* head)
{
if(head==NULL)
return false;
node *low=head, *fast=head->next;
while(fast!=NULL && fast->next!=NULL)
{
low=low->next;
fast=fast->next->next;
if(low==fast) return true;
}
return false;
}
//如果链表可能有环,则如何判断两个链表是否相交
//思路:链表1 步长为1,链表2步长为2 ,如果有环且相交则肯定相遇,否则不相交
list1 head: p1
list2 head: p2
while( p1 != p2 && p1 != NULL && p2 != NULL )
[b]//但当链表有环但不相交时,此处是死循环。![/b]
{
p1 = p1->next;
if ( p2->next )
p2 = p2->next->next;
else
p2 = p2->next;
}
if ( p1 == p2 && p1 && p2)
//相交
else
//不相交
[color=#FF0000][b]所以,判断带环的链表,相不相交,只能这样[/b]:[/color]
如果都带环,判断一链表上俩指针相遇的那个节点,在不在另一条链表上。
如果在,则相交,如果不在,则不相交。(未写代码实现,见谅。:)..
------------------
第9题
-----------------------------------
判断整数序列是不是二元查找树的后序遍历结果
题目:输入一个整数数组,判断该数组是不是某二元查找树的后序遍历的结果。
如果是返回true,否则返回false。
例如输入5、7、6、9、11、10、8,由于这一整数序列是如下树的后序遍历结果:
8
/ /
6 10
/ / / /
5 7 9 11
因此返回true。
如果输入7、4、6、5,没有哪棵树的后序遍历的结果是这个序列,因此返回false。
//貌似,少有人关注此题。:).2010/10/18
bool verifySquenceOfBST(int squence[], int length)
{
if(squence == NULL || length <= 0)
return false;
// root of a BST is at the end of post order traversal squence
int root = squence[length - 1];
// the nodes in left sub-tree are less than the root
int i = 0;
for(; i < length - 1; ++ i)
{
if(squence[i] > root)
break;
}
// the nodes in the right sub-tree are greater than the root
int j = i;
for(; j < length - 1; ++ j)
{
if(squence[j] < root)
return false;
}
// verify whether the left sub-tree is a BST
bool left = true;
if(i > 0)
left = verifySquenceOfBST(squence, i);
// verify whether the right sub-tree is a BST
bool right = true;
if(i < length - 1)
right = verifySquenceOfBST(squence + i, length - i - 1);
return (left && right);
}
第9题:
其实,就是一个后序遍历二叉树的算法。
关键点:
1.
//确定根结点
int root = squence[length - 1];
2.
// the nodes in left sub-tree are less than the root
int i = 0;
for(; i < length - 1; ++ i)
{
if(squence[i] > root)
break;
}
// the nodes in the right sub-tree are greater than the root
int j = i;
for(; j < length - 1; ++ j)
{
if(squence[j] < root)
return false;
}
3.
递归遍历,左右子树。
---------------------------------------
//第10题,单词翻转。
//单词翻转,引用自117 楼 wocaoqwer 的回复。
#include<iostream>
#include<string>
using namespace std;
class ReverseWords{
public:
ReverseWords(string* wo):words(wo){}
void reverse_()
{
int length=words->size();
int begin=-1,end=-1;
for(int i=0;i<length;++i){
if(begin==-1&&words->at(i)==' ')
continue;
if(begin==-1)
{
begin=i;
continue;
}
if(words->at(i)==' ')
end=i-1;
else if(i==length-1)
end=i;
else
continue;
reverse__(begin,end); //1.字母翻转
begin=-1,end=-1;
}
reverse__(0,length-1); //2.单词翻转
}
private:
void reverse__(int begin,int end) //
{
while(begin<end)
{
char t=words->at(begin);
words->at(begin)=words->at(end);
words->at(end)=t;
++begin;
--end;
}
}
string* words;
};
int main(){
string s="I am a student.";
ReverseWords r(&s);
r.reverse_();
cout<<s<<endl;
return 0;
}
运行结果:
student. a am I
Press any key to continue
第11题
------------------------------------
求二叉树中节点的最大距离...
如果我们把二叉树看成一个图,
父子节点之间的连线看成是双向的,
我们姑且定义"距离"为两节点之间边的个数。
写一个程序,
求一棵二叉树中相距最远的两个节点之间的距离。
//July 2010/10/19
//此题思路,tree_star and i 在257、258楼,讲的很明白了。
//定义一个结构体
struct NODE
{
NODE* pLeft;
NODE* pRight;
int MaxLen;
int MaxRgt;
};
NODE* pRoot; //根节点
int MaxLength;
void traversal_MaxLen(NODE* pRoot)
{
if(pRoot == NULL)
{
return 0;
};
if(pRoot->pLeft == NULL)
{
pRoot->MaxLeft = 0;
}
else //若左子树不为空
{
int TempLen = 0;
if(pRoot->pLeft->MaxLeft > pRoot->pLeft->MaxRight)
//左子树上的,某一节点,往左边大,还是往右边大
{
TempLen+=pRoot->pLeft->MaxLeft;
}
else
{
TempLen+=pRoot->pLeft->MaxRight;
}
pRoot->nMaxLeft = TempLen + 1;
traversal_MaxLen(NODE* pRoot->pLeft);
//此处,加上递归
}
if(pRoot->pRigth == NULL)
{
pRoot->MaxRight = 0;
}
else //若右子树不为空
{
int TempLen = 0;
if(pRoot->pRight->MaxLeft > pRoot->pRight->MaxRight)
//右子树上的,某一节点,往左边大,还是往右边大
{
TempLen+=pRoot->pRight->MaxLeft;
}
else
{
TempLen+=pRoot->pRight->MaxRight;
}
pRoot->MaxRight = TempLen + 1;
traversal_MaxLen(NODE* pRoot->pRight);
//此处,加上递归
}
if(pRoot->MaxLeft + pRoot->MaxRight > 0)
{
MaxLength=pRoot->nMaxLeft + pRoot->MaxRight;
}
}
// 数据结构定义
struct NODE
{
NODE* pLeft; // 左子树
NODE* pRight; // 右子树
int nMaxLeft; // 左子树中的最长距离
int nMaxRight; // 右子树中的最长距离
char chValue; // 该节点的值
};
int nMaxLen = 0;
// 寻找树中最长的两段距离
void FindMaxLen(NODE* pRoot)
{
// 遍历到叶子节点,返回
if(pRoot == NULL)
{
return;
}
// 如果左子树为空,那么该节点的左边最长距离为0
if(pRoot -> pLeft == NULL)
{
pRoot -> nMaxLeft = 0;
}
// 如果右子树为空,那么该节点的右边最长距离为0
if(pRoot -> pRight == NULL)
{
pRoot -> nMaxRight = 0;
}
// 如果左子树不为空,递归寻找左子树最长距离
if(pRoot -> pLeft != NULL)
{
FindMaxLen(pRoot -> pLeft);
}
// 如果右子树不为空,递归寻找右子树最长距离
if(pRoot -> pRight != NULL)
{
FindMaxLen(pRoot -> pRight);
}
// 计算左子树最长节点距离
if(pRoot -> pLeft != NULL)
{
int nTempMax = 0;
if(pRoot -> pLeft -> nMaxLeft > pRoot -> pLeft -> nMaxRight)
{
nTempMax = pRoot -> pLeft -> nMaxLeft;
}
else
{
nTempMax = pRoot -> pLeft -> nMaxRight;
}
pRoot -> nMaxLeft = nTempMax + 1;
}
// 计算右子树最长节点距离
if(pRoot -> pRight != NULL)
{
int nTempMax = 0;
if(pRoot -> pRight -> nMaxLeft > pRoot -> pRight -> nMaxRight)
{
nTempMax = pRoot -> pRight -> nMaxLeft;
}
else
{
nTempMax = pRoot -> pRight -> nMaxRight;
}
pRoot -> nMaxRight = nTempMax + 1;
}
// 更新最长距离
if(pRoot -> nMaxLeft + pRoot -> nMaxRight > nMaxLen)
{
nMaxLen = pRoot -> nMaxLeft + pRoot -> nMaxRight;
}
}
//很明显,思路完全一样,但书上给的这段代码更规范!:)。
第12题
题目:求1+2+…+n,
要求不能使用乘除法、for、while、if、else、switch、case等关键字
以及条件判断语句(A?B:C)。
//July、2010/10/19
-----------------
循环只是让相同的代码执行n遍而已,我们完全可以不用for和while达到这个效果。
比如定义一个类,我们new一含有n个这种类型元素的数组,
那么该类的构造函数将确定会被调用n次。我们可以将需要执行的代码放到构造函数里。
------------------
#include <iostream.h>
class Temp
{
public:
Temp()
{
++N;
Sum += N;
}
static void Reset() { N = 0; Sum = 0; }
static int GetSum() { return Sum; }
private:
static int N;
static int Sum;
};
int Temp::N = 0;
int Temp::Sum = 0;
int solution1_Sum(int n)
{
Temp::Reset();
Temp *a = new Temp[n]; //就是这个意思,new出n个数组。
delete []a;
a = 0;
return Temp::GetSum();
}
int main()
{
cout<<solution1_Sum(100)<<endl;
return 0;
}
//运行结果:
//5050
//Press any key to continue
//July、2010/10/19
//第二种思路:
----------------
既然不能判断是不是应该终止递归,我们不妨定义两个函数。
一个函数充当递归函数的角色,另一个函数处理终止递归的情况,
我们需要做的就是在两个函数里二选一。
从二选一我们很自然的想到布尔变量,
比如ture/(1)的时候调用第一个函数,false/(0)的时候调用第二个函数。
那现在的问题是如和把数值变量n转换成布尔值。
如果对n连续做两次反运算,即!!n,那么非零的n转换为true,0转换为false。
#include <iostream.h>
class A;
A* Array[2];
class A
{
public:
virtual int Sum (int n) { return 0; }
};
class B: public A
{
public:
virtual int Sum (int n) { return Array[!!n]->Sum(n-1)+n; }
};
int solution2_Sum(int n)
{
A a;
B b;
Array[0] = &a;
Array[1] = &b;
int value = Array[1]->Sum(n);
//利用虚函数的特性,当Array[1]为0时,即Array[0] = &a; 执行A::Sum,
//当Array[1]不为0时, 即Array[1] = &b; 执行B::Sum。
return value;
}
int main()
{
cout<<solution2_Sum(100)<<endl;
return 0;
}
//5050
//Press any key to continue
第13题:
题目:
输入一个单向链表,输出该链表中倒数第k个结点,
链表的倒数第0个结点为链表的尾指针。
//此题一出,相信,稍微有点 经验的同志,都会说到:
------------------------
设置两个指针p1,p2
首先p1和p2都指向head
然后p2向前走n步,这样p1和p2之间就间隔k个节点
然后p1和p2同……
#include <iostream.h>
#include <stdio.h>
#include <stdlib.h>
struct ListNode
{
char data;
ListNode* next;
};
ListNode* head,*p,*q;
ListNode *pone,*ptwo;
ListNode* fun(ListNode *head,int k)
{
pone = ptwo = head;
for(int i=0;i<=k-1;i++)
ptwo=ptwo->next;
while(ptwo!=NULL)
{
pone=pone->next;
ptwo=ptwo->next;
}
return pone;
}
int main()
{
char c;
head = (ListNode*)malloc(sizeof(ListNode));
head->next = NULL;
p = head;
while(c !='0')
{
q = (ListNode*)malloc(sizeof(ListNode));
q->data = c;
q->next = NULL;
p->next = q;
p = p->next;
c = getchar();
}
cout<<"---------------"<<endl;
cout<<fun(head,2)->data<<endl;
return 0;
}
/////
1254863210
---------------
2
Press any key to continue
////
第14题:
题目:输入一个已经按升序排序过的数组和一个数字,
在数组中查找两个数,使得它们的和正好是输入的那个数字。
要求时间复杂度是O(n)。
如果有多对数字的和等于输入的数字,输出任意一对即可。
例如输入数组1、2、4、7、11、15和数字15。由于4+11=15,因此输出4和11。
//由于数组已经过升序排列,所以,难度下降了不少。
//July、2010/10/19
#include <iostream.h>
bool FindTwoNumbersWithSum
(
int data[], // 已经排序的 数组
unsigned int length, // 数组长度
int sum, //用户输入的 sum
int& num1, // 输出符合和等于sum的第一个数
int& num2 // 第二个数
)
{
bool found = false;
if(length < 1)
return found;
int begin = 0;
int end = length - 1;
while(end > begin)
{
long curSum = data[begin] + data[end];
if(curSum == sum)
{
num1 = data[begin];
num2 = data[end];
found = true;
break;
}
else if(curSum > sum)
end--;
else
begin++;
}
return found;
}
int main()
{
int x,y;
int a[6]={1,2,4,7,11,15};
if(FindTwoNumbersWithSum(a,6,15,x,y) )
{
cout<<x<<endl<<y<<endl;
}
return 0;
}
4
11
Press any key to continue
//扩展:如果输入的数组是没有排序的,但知道里面数字的范围,其他条件不变,
//如何在O(n)时间里找到这两个数字?
关于第14题,
1.题目假定是,只要找出俩个数,的和等于给定的数,
其实是,当给定一排数,
4,5,7,10,12
然后给定一个数,22。
就有俩种可能了。因为22=10+12=10+5+7。
而恰恰与第4题,有关联了。望大家继续思考下。:)。
2.第14题,还有一种思路,如下俩个数组:
1、 2、 4、7、11、15 //用15减一下为
14、13、11、8、4、 0 //如果下面出现了和上面一样的数,稍加判断,就能找出这俩个数来了。
第一个数组向右扫描,第二个数组向左扫描。
第15题:
题目:输入一颗二元查找树,将该树转换为它的镜像,
即在转换后的二元查找树中,左子树的结点都大于右子树的结点。
用递归和循环两种方法完成树的镜像转换。
例如输入:
8
/ /
6 10
/ / / /
5 7 9 11
输出:
8
/ /
10 6
/ / / /
11 9 7 5
定义二元查找树的结点为:
struct BSTreeNode // a node in the binary search tree (BST)
{
int m_nValue; // value of node
BSTreeNode *m_pLeft; // left child of node
BSTreeNode *m_pRight; // right child of node
};
//就是递归翻转树,有子树则递归翻转子树。
//July、2010/10/19
void Revertsetree(list *root)
{
if(!root)
return;
list *p;
p=root->leftch;
root->leftch=root->rightch;
root->rightch=p;
if(root->leftch)
Revertsetree(root->leftch);
if(root->rightch)
Revertsetree(root->rightch);
}
由于递归的本质是编译器生成了一个函数调用的栈,
因此用循环来完成同样任务时最简单的办法就是用一个辅助栈来模拟递归。
首先我们把树的头结点放入栈中。
在循环中,只要栈不为空,弹出栈的栈顶结点,交换它的左右子树。
如果它有左子树,把它的左子树压入栈中;
如果它有右子树,把它的右子树压入栈中。
这样在下次循环中就能交换它儿子结点的左右子树了。
//再用辅助栈模拟递归,改成循环的(有误之处,望不吝指正):
void Revertsetree(list *phead)
{
if(!phead)
return;
stack<list*> stacklist;
stacklist.push(phead); //首先把树的头结点放入栈中。
while(stacklist.size())
//在循环中,只要栈不为空,弹出栈的栈顶结点,交换它的左右子树
{
list* pnode=stacklist.top();
stacklist.pop();
list *ptemp;
ptemp=pnode->leftch;
pnode->leftch=pnode->rightch;
pnode->rightch=ptemp;
if(pnode->leftch)
stacklist.push(pnode->leftch); //若有左子树,把它的左子树压入栈中
if(pnode->rightch)
stacklist.push(pnode->rightch); //若有右子树,把它的右子树压入栈中
}
}
第16题
题目:输入一颗二元树,从上往下按层打印树的每个结点,同一层中按照从左往右的顺序打印。
例如输入
8
/ /
6 10
// //
5 7 9 11
输出8 6 10 5 7 9 11。
//题目不是我们所熟悉的,树的前序,中序,后序。即是树的层次遍历。
/*308 楼 panda_lin 的回复,说的已经很好了。:)
利用队列,每个单元对应二叉树的一个节点.
1:输出8, 队列内容: 6, 10
2:输出6, 6的2个子节点5,7入队列。队列的内容:10, 5, 7
3:输出10,10的2个子节点9,11入队列。队列的内容:5,7,9,11。
4:输出5 ,5没有子节点。队列的内容:7,9,11
5:。。。
由于STL已经为我们实现了一个很好的deque(两端都可以进出的队列),
我们只需要拿过来用就可以了。
我们知道树是图的一种特殊退化形式。
同时如果对图的深度优先遍历和广度优先遍历有比较深刻的理解,
将不难看出这种遍历方式实际上是一种广度优先遍历。
因此这道题的本质是在二元树上实现广度优先遍历。
//July、2010/10/19/晚。
#include <deque>
#include <iostream>
using namespace std;
struct BTreeNode // a node in the binary tree
{
int m_nValue; // value of node
BTreeNode *m_pLeft; // left child of node
BTreeNode *m_pRight; // right child of node
};
BTreeNode* pListIndex;
BTreeNode* pHead;
void PrintFromTopToBottom(BTreeNode *pTreeRoot)
{
if(!pTreeRoot)
return;
// get a empty queue
deque<BTreeNode *> dequeTreeNode;
// insert the root at the tail of queue
dequeTreeNode.push_back(pTreeRoot);
while(dequeTreeNode.size())
{
// get a node from the head of queue
BTreeNode *pNode = dequeTreeNode.front();
dequeTreeNode.pop_front();
// print the node
cout << pNode->m_nValue << ' ';
// print its left child sub-tree if it has
if(pNode->m_pLeft)
dequeTreeNode.push_back(pNode->m_pLeft);
// print its right child sub-tree if it has
if(pNode->m_pRight)
dequeTreeNode.push_back(pNode->m_pRight);
}
}
// 创建二元查找树
void addBTreeNode(BTreeNode * & pCurrent, int value)
{
if (NULL == pCurrent)
{
BTreeNode * pBTree = new BTreeNode();
pBTree->m_pLeft = NULL;
pBTree->m_pRight = NULL;
pBTree->m_nValue = value;
pCurrent = pBTree;
}
else
{
if ((pCurrent->m_nValue) > value)
{
addBTreeNode(pCurrent->m_pLeft, value);
}
else if ((pCurrent->m_nValue) < value)
{
addBTreeNode(pCurrent->m_pRight, value);
}
}
}
int main()
{
BTreeNode * pRoot = NULL;
pListIndex = NULL;
pHead = NULL;
addBTreeNode(pRoot, 8);
addBTreeNode(pRoot, 6);
addBTreeNode(pRoot, 5);
addBTreeNode(pRoot, 7);
addBTreeNode(pRoot, 10);
addBTreeNode(pRoot, 9);
addBTreeNode(pRoot, 11);
PrintFromTopToBottom(pRoot);
return 0;
}
//输出结果:
//8 6 10 5 7 9 11 Press any key to continue
是的,由这道题,突然想到了,树的广度优先遍历,BFS算法,
算法王帖:精选经典的24个算法 [3.BFS和DFS优先搜索]
http://blog.sina.com.cn/s/blog_5e3ab00c0100lya2.html
第17题:
题目:在一个字符串中找到第一个只出现一次的字符。
如输入abaccdeff,则输出b。
这道题是2006年google的一道笔试题。
思路剖析:由于题目与字符出现的次数相关,我们可以统计每个字符在该字符串中出现的次数.
要达到这个目的,需要一个数据容器来存放每个字符的出现次数。
在这个数据容器中可以根据字符来查找它出现的次数,
也就是说这个容器的作用是把一个字符映射成一个数字。
在常用的数据容器中,哈希表正是这个用途。
由于本题的特殊性,我们只需要一个非常简单的哈希表就能满足要求。
由于字符(char)是一个长度为8的数据类型,因此总共有可能256 种可能。
于是我们创建一个长度为256的数组,每个字母根据其ASCII码值作为数组的下标对应数组的对应项,
而数组中存储的是每个字符对应的次数。
这样我们就创建了一个大小为256,以字符ASCII码为键值的哈希表。
我们第一遍扫描这个数组时,每碰到一个字符,在哈希表中找到对应的项并把出现的次数增加一次。
这样在进行第二次扫描时,就能直接从哈希表中得到每个字符出现的次数了。
//July、2010/10/20
#include <iostream.h>
#include <string.h>
char FirstNotRepeatingChar(char* pString)
{
if(!pString)
return 0;
const int tableSize = 256;
unsigned int hashTable[tableSize];
for(unsigned int i = 0; i < tableSize; ++ i)
hashTable[i] = 0;
char* pHashKey = pString;
while(*(pHashKey) != '/0')
hashTable[*(pHashKey++)] ++;
pHashKey = pString;
while(*pHashKey != '/0')
{
if(hashTable[*pHashKey] == 1)
return *pHashKey;
pHashKey++;
}
return *pHashKey;
}
int main()
{
cout<<"请输入一串字符:"<<endl;
char s[100];
cin>>s;
char* ps=s;
cout<<FirstNotRepeatingChar(ps)<<endl;
return 0;
}
//
请输入一串字符:
abaccdeff
b
Press any key to continue
///
第18题:
题目:n个数字(0,1,…,n-1)形成一个圆圈,从数字0开始,
每次从这个圆圈中删除第m个数字(第一个为当前数字本身,第二个为当前数字的下一个数字)。
当一个数字删除后,从被删除数字的下一个继续删除第m个数字。
求出在这个圆圈中剩下的最后一个数字。
July:我想,这个题目,不少人已经 见识过了。
先看这个题目的简单变形。
n个人围成一圈,顺序排号。从第一个人开始报数(从1到3报数),
凡报到3的人退出圈子,问最后留下的是原来第几号的那个人?
---------------------------------------------------------
//July、2010/10/20
//我把这100题,当每日必须完成的作业,来做了。:)。
#include <stdio.h>int main()
{
int i,k,m,n,num[50],*p;
printf("input number of person:n=");
scanf("%d",&n);printf("input number of the quit:m="); //留下->18题
scanf("%d",&m); //留下->18题p=num;
for(i=0;i<n;i++)
*(p+i)=i+1; //给每个人编号
i=0; //报数
k=0; //此处为3
// m=0; //m为退出人数 //去掉->18题
while(m<n-1)
{
if(*(p+i)!=0)
k++;
if(k==3)
{
*(p+i)=0; //退出,对应的数组元素置为0
k=0;
m++;
}
i++;
if(i==n)
i=0;
}
while(*p==0)
p++;
printf("The last one is NO.%d/n",*p);
}
//
int LastRemaining_Solution2(int n, unsigned int m)
{
// invalid input
if(n <= 0 || m < 0)
return -1;// if there are only one integer in the circle initially,
// of course the last remaining one is 0
int lastinteger = 0;// find the last remaining one in the circle with n integers
for (int i = 2; i <= n; i ++)
lastinteger = (lastinteger + m) % i;return lastinteger;
}
第19题:
题目:定义Fibonacci数列如下:
/ 0 n=0
f(n)= 1 n=1,2
/ f(n-1)+f(n-2) n>2
输入n,用最快的方法求该数列的第n项。
分析:在很多C语言教科书中讲到递归函数的时候,都会用Fibonacci作为例子。
因此很多程序员对这道题的递归解法非常熟悉,但....呵呵,你知道的。。
//0 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597..........
//注意,当求第100项,甚至更大的项时,请确保你用什么类型,长整型?or long long int存储。
//不然,计算机,将 得不到结果。
//若用递归方法,可写 下如下代码:
#include <iostream.h>int Fibona(int n)
{
int m;
if(n==0)
return 0;
else if(n==1||n==2)
return 1;
else
{
m=Fibona(n-1)+Fibona(n-2);
return m;
}
}int main()
{
cout<<"-----------------"<<endl;
cout<<Fibona(17)<<endl;
return 0;
}
---------------------------
科书上反复用这个题目来讲解递归函数,并不能说明递归解法最适合这道题目。
我们以求解f(10)作为例子来分析递归求解的过程。
要求得f(10),需要求得f(9)和f(8)。同样,要求得f(9),要先求得f(8)和f(7)……
我们用树形结构来表示这种依赖关系
f(10)
/ /
f(9) f(8)
/ / / /
f(8) f(7) f(6) f(5)
/ / / /
f(7) f(6) f(6) f(5)更简单的办法是从下往上计算,首先根据f(0)和f(1)算出f(2),再根据f(1)和f(2)算出f(3)……
依此类推就可以算出第n项了。很容易理解,这种思路的时间复杂度是O(n)。其实,就是转化为非递归程序,用递推。!
------------------------------------------
long long Fibonacci_Solution2(unsigned n)
{
int result[2] = {0, 1};
if(n < 2)
return result[n];long long fibNMinusOne = 1;
long long fibNMinusTwo = 0;
long long fibN = 0;
for(unsigned int i = 2; i <= n; ++ i)
{
fibN = fibNMinusOne + fibNMinusTwo;fibNMinusTwo = fibNMinusOne;
fibNMinusOne = fibN;
}return fibN;
}
//很可惜,这还不是最快的方法。
//还有一种方法,可达到,时间复杂度为O(lgn).
//............
第20题:
题目:输入一个表示整数的字符串,把该字符串转换成整数并输出。
例如输入字符串"345",则输出整数345。
-----------------------------
此题一点也不简单。不信,你就先不看一下的代码,
你自己先写一份,然后再对比一下,便知道了。
1.转换的思路:每扫描到一个字符,我们把在之前得到的数字乘以10再加上当前字符表示的数字。
这个思路用循环不难实现。
2.由于整数可能不仅仅之含有数字,还有可能以'+'或者'-'开头,表示整数的正负。
如果第一个字符是'+'号,则不需要做任何操作;如果第一个字符是'-'号,
则表明这个整数是个负数,在最后的时候我们要把得到的数值变成负数。
3.接着我们试着处理非法输入。由于输入的是指针,在使用指针之前,
我们要做的第一件是判断这个指针是不是为空。
如果试着去访问空指针,将不可避免地导致程序崩溃。
4.输入的字符串中可能含有不是数字的字符。
每当碰到这些非法的字符,我们就没有必要再继续转换。
最后一个需要考虑的问题是溢出问题。由于输入的数字是以字符串的形式输入,
因此有可能输入一个很大的数字转换之后会超过能够表示的最大的整数而溢出。
//July、2010、10/22。
enum Status {kValid = 0, kInvalid};
int g_nStatus = kValid;int StrToInt(const char* str)
{
g_nStatus = kInvalid;
long long num = 0;if(str != NULL)
{
const char* digit = str;// the first char in the string maybe '+' or '-'
bool minus = false;
if(*digit == '+')
digit ++;
else if(*digit == '-')
{
digit ++;
minus = true;
}// the remaining chars in the string
while(*digit != '/0')
{
if(*digit >= '0' && *digit <= '9')
{
num = num * 10 + (*digit - '0');// overflow
if(num > std::numeric_limits<int>::max())
{
num = 0;
break;
}digit ++;
}
// if the char is not a digit, invalid input
else
{
num = 0;
break;
}
}if(*digit == '/0')
{
g_nStatus = kValid;
if(minus)
num = 0 - num;
}
}
return static_cast<int>(num);
}
//在C语言提供的库函数中,函数atoi能够把字符串转换整数。
//它的声明是int atoi(const char *str)。该函数就是用一个全局变量来标志输入是否合法的。
其中,部分题目源码及思路,参考自:http://blog.csdn.net/zajin
精选微软等公司数据结构+算法面试100题[第1-60题汇总]
精选微软等公司数据结构+算法面试100题
-----[第1题-60题总]
--------------------------------
相关资源,下载地址:
[第1题-60题汇总]微软等数据结构+算法面试100题
http://download.csdn.net/source/2826690
帖子维护地址:
[整理]算法面试:精选微软经典的算法面试100题[前1-60题]
http://topic.csdn.net/u/20101023/20/5652ccd7-d510-4c10-9671-307a56006e6d.html
懒得写了。题目都在上述帖子上,或请下载资源。
--------------------------------------------------------------------------------------------------
以上是前期,所写的。在此,我特意,将第1-60题,再重新整理下。
以感谢Csdn的推荐。谢谢。
感谢Csdn对另外俩篇文章(即本微软等100题系列) 的推荐。
--------------- --------------
1.把二元查找树转变成排序的双向链表
题目:
输入一棵二元查找树,将该二元查找树转换成一个排序的双向链表。
要求不能创建任何新的结点,只调整指针的指向。
10
/ /
6 14
/ / / /
4 8 12 16
转换成双向链表
4=6=8=10=12=14=16。
首先我们定义的二元查找树 节点的数据结构如下:
struct BSTreeNode
{
int m_nValue; // value of node
BSTreeNode *m_pLeft; // left child of node
BSTreeNode *m_pRight; // right child of node
};
2.设计包含min函数的栈。
定义栈的数据结构,要求添加一个min函数,能够得到栈的最小元素。
要求函数min、push以及pop的时间复杂度都是O(1)。
3.求子数组的最大和
题目:
输入一个整形数组,数组里有正数也有负数。
数组中连续的一个或多个整数组成一个子数组,每个子数组都有一个和。
求所有子数组的和的最大值。要求时间复杂度为O(n)。
例如输入的数组为1, -2, 3, 10, -4, 7, 2, -5,和最大的子数组为3, 10, -4, 7, 2,
因此输出为该子数组的和18。
4.在二元树中找出和为某一值的所有路径
题目:输入一个整数和一棵二元树。
从树的根结点开始往下访问一直到叶结点所经过的所有结点形成一条路径。
打印出和与输入整数相等的所有路径。
例如 输入整数22和如下二元树
10
/ /
5 12
/ /
4 7
则打印出两条路径:10, 12和10, 5, 7。
二元树节点的数据结构定义为:
struct BinaryTreeNode // a node in the binary tree
{
int m_nValue; // value of node
BinaryTreeNode *m_pLeft; // left child of node
BinaryTreeNode *m_pRight; // right child of node
};
5.查找最小的k个元素
题目:输入n个整数,输出其中最小的k个。
例如输入1,2,3,4,5,6,7和8这8个数字,则最小的4个数字为1,2,3和4。
第6题
------------------------------------
腾讯面试题:
给你10分钟时间,根据上排给出十个数,在其下排填出对应的十个数
要求下排每个数都是先前上排那十个数在下排出现的次数。
上排的十个数如下:
【0,1,2,3,4,5,6,7,8,9】
初看此题,貌似很难,10分钟过去了,可能有的人,题目都还没看懂。
举一个例子,
数值: 0,1,2,3,4,5,6,7,8,9
分配: 6,2,1,0,0,0,1,0,0,0
0在下排出现了6次,1在下排出现了2次,
2在下排出现了1次,3在下排出现了0次....
以此类推..
第7题
------------------------------------
微软亚院之编程判断俩个链表是否相交
给出俩个单向链表的头指针,比如h1,h2,判断这俩个链表是否相交。
为了简化问题,我们假设俩个链表均不带环。
问题扩展:
1.如果链表可能有环列?
2.如果需要求出俩个链表相交的第一个节点列?
第8题
------------------------------------
此贴选一些 比较怪的题,,由于其中题目本身与算法关系不大,仅考考思维。特此并作一题。
1.有两个房间,一间房里有三盏灯,另一间房有控制着三盏灯的三个开关,这两个房间是 分割开的,
从一间里不能看到另一间的情况。
现在要求受训者分别进这两房间一次,然后判断出这三盏灯分别是由哪个开关控制的。
有什么办法呢?
2.你让一些人为你工作了七天,你要用一根金条作为报酬。金条被分成七小块,每天给出一块。
如果你只能将金条切割两次,你怎样分给这些工人?
3 ★用一种算法来颠倒一个链接表的顺序。现在在不用递归式的情况下做一遍。
★用一种算法在一个循环的链接表里插入一个节点,但不得穿越链接表。
★用一种算法整理一个数组。你为什么选择这种方法?
★用一种算法使通用字符串相匹配。
★颠倒一个字符串。优化速度。优化空间。
★颠倒一个句子中的词的顺序,比如将“我叫克丽丝”转换为“克丽丝叫我”,实现速度最快,移动最少。
★找到一个子字符串。优化速度。优化空间。
★比较两个字符串,用O(n)时间和恒量空间。
★假设你有一个用1001个整数组成的数组,这些整数是任意排列的,但是你知道所有的整数都在1到1000(包括1000)之间。
此外,除一个数字出现两次外,其他所有数字只出现一次
。假设你只能对这个数组做一次处理,用一种算法找出重复的那个数字。
如果你在运算中使用了辅助的存储方式,那么你能找到不用这种方式的算法吗?
★不用乘法或加法增加8倍。现在用同样的方法增加7倍。
第9题
判断整数序列是不是二元查找树的后序遍历结果
题目:输入一个整数数组,判断该数组是不是某二元查找树的后序遍历的结果。
如果是返回true,否则返回false。
例如输入5、7、6、9、11、10、8,由于这一整数序列是如下树的后序遍历结果:
8
/ /
6 10
/ / / /
5 7 9 11
因此返回true。
如果输入7、4、6、5,没有哪棵树的后序遍历的结果是这个序列,因此返回false。
第10题
翻转句子中单词的顺序。
题目:输入一个英文句子,翻转句子中单词的顺序,但单词内字符的顺序不变。句子中单词以空格符隔开。
为简单起见,标点符号和普通字母一样处理。
例如输入“I am a student.”,则输出“student. a am I”。
第11题
求二叉树中节点的最大距离...
如果我们把二叉树看成一个图,
父子节点之间的连线看成是双向的,
我们姑且定义"距离"为两节点之间边的个数。
写一个程序,
求一棵二叉树中相距最远的两个节点之间的距离。
第12题
题目:求1+2+…+n,
要求不能使用乘除法、for、while、if、else、switch、case等关键字以及条件判断语句(A?B:C)。
第13题:
题目:输入一个单向链表,输出该链表中倒数第k个结点。链表的倒数第0个结点为链表的尾指针。
链表结点定义如下:
struct ListNode
{
int m_nKey;
ListNode* m_pNext;
};
第14题:
题目:输入一个已经按升序排序过的数组和一个数字,
在数组中查找两个数,使得它们的和正好是输入的那个数字。
要求时间复杂度是O(n)。如果有多对数字的和等于输入的数字,输出任意一对即可。
例如输入数组1、2、4、7、11、15和数字15。由于4+11=15,因此输出4和11。
第15题:
题目:输入一颗二元查找树,将该树转换为它的镜像,
即在转换后的二元查找树中,左子树的结点都大于右子树的结点。
用递归和循环两种方法完成树的镜像转换。
例如输入:
8
/ /
6 10
// //
5 7 9 11
输出:
8
/ /
10 6
// //
11 9 7 5
定义二元查找树的结点为:
struct BSTreeNode // a node in the binary search tree (BST)
{
int m_nValue; // value of node
BSTreeNode *m_pLeft; // left child of node
BSTreeNode *m_pRight; // right child of node
};
第16题:
题目(微软):
输入一颗二元树,从上往下按层打印树的每个结点,同一层中按照从左往右的顺序打印。
例如输入
8
/ /
6 10
/ / / /
5 7 9 11
输出8 6 10 5 7 9 11。
第17题:
题目:在一个字符串中找到第一个只出现一次的字符。如输入abaccdeff,则输出b。
分析:这道题是2006年google的一道笔试题。
第18题:
题目:n个数字(0,1,…,n-1)形成一个圆圈,从数字0开始,
每次从这个圆圈中删除第m个数字(第一个为当前数字本身,第二个为当前数字的下一个数字)。
当一个数字删除后,从被删除数字的下一个继续删除第m个数字。
求出在这个圆圈中剩下的最后一个数字。
July:我想,这个题目,不少人已经 见识过了。
第19题:
题目:定义Fibonacci数列如下:
/ 0 n=0
f(n)= 1 n=1
/ f(n-1)+f(n-2) n=2
输入n,用最快的方法求该数列的第n项。
分析:在很多C语言教科书中讲到递归函数的时候,都会用Fibonacci作为例子。
因此很多程序员对这道题的递归解法非常熟悉,但....呵呵,你知道的。。
第20题:
题目:输入一个表示整数的字符串,把该字符串转换成整数并输出。
例如输入字符串"345",则输出整数345。
第21题
2010年中兴面试题
编程求解:
输入两个整数 n 和 m,从数列1,2,3.......n 中 随意取几个数,
使其和等于 m ,要求将其中所有的可能组合列出来.
第22题:
有4张红色的牌和4张蓝色的牌,主持人先拿任意两张,再分别在A、B、C三人额头上贴任意两张牌,
A、B、C三人都可以看见其余两人额头上的牌,看完后让他们猜自己额头上是什么颜色的牌,
A说不知道,B说不知道,C说不知道,然后A说知道了。
请教如何推理,A是怎么知道的。
如果用程序,又怎么实现呢?
第23题:
用最简单, 最快速的方法计算出下面这个圆形是否和正方形相交。"
3D坐标系 原点(0.0,0.0,0.0)
圆形:
半径r = 3.0
圆心o = (*.*, 0.0, *.*)
正方形:
4个角坐标;
1:(*.*, 0.0, *.*)
2:(*.*, 0.0, *.*)
3:(*.*, 0.0, *.*)
4:(*.*, 0.0, *.*)
第24题:
链表操作,
(1).单链表就地逆置,
(2)合并链表
第25题:
写一个函数,它的原形是int continumax(char *outputstr,char *intputstr)
功能:
在字符串中找出连续最长的数字串,并把这个串的长度返回,
并把这个最长数字串付给其中一个函数参数outputstr所指内存。
例如:"abcd12345ed125ss123456789"的首地址传给intputstr后,函数将返回9,
outputstr所指的值为123456789
26.左旋转字符串
题目:
定义字符串的左旋转操作:把字符串前面的若干个字符移动到字符串的尾部。
如把字符串abcdef左旋转2位得到字符串cdefab。请实现字符串左旋转的函数。
要求时间对长度为n的字符串操作的复杂度为O(n),辅助内存为O(1)。
27.跳台阶问题
题目:一个台阶总共有n级,如果一次可以跳1级,也可以跳2级。
求总共有多少总跳法,并分析算法的时间复杂度。
这道题最近经常出现,包括MicroStrategy等比较重视算法的公司都
曾先后选用过个这道题作为面试题或者笔试题。
28.整数的二进制表示中1的个数
题目:输入一个整数,求该整数的二进制表达中有多少个1。
例如输入10,由于其二进制表示为1010,有两个1,因此输出2。
分析:
这是一道很基本的考查位运算的面试题。
包括微软在内的很多公司都曾采用过这道题。
29.栈的push、pop序列
题目:输入两个整数序列。其中一个序列表示栈的push顺序,
判断另一个序列有没有可能是对应的pop顺序。
为了简单起见,我们假设push序列的任意两个整数都是不相等的。
比如输入的push序列是1、2、3、4、5,那么4、5、3、2、1就有可能是一个pop系列。
因为可以有如下的push和pop序列:
push 1,push 2,push 3,push 4,pop,push 5,pop,pop,pop,pop,
这样得到的pop序列就是4、5、3、2、1。
但序列4、3、5、1、2就不可能是push序列1、2、3、4、5的pop序列。
30.在从1到n的正数中1出现的次数
题目:输入一个整数n,求从1到n这n个整数的十进制表示中1出现的次数。
例如输入12,从1到12这些整数中包含1 的数字有1,10,11和12,1一共出现了5次。
分析:这是一道广为流传的google面试题。
31.华为面试题:
一类似于蜂窝的结构的图,进行搜索最短路径(要求5分钟)
32.
有两个序列a,b,大小都为n,序列元素的值任意整数,无序;
要求:通过交换a,b中的元素,使[序列a元素的和]与[序列b元素的和]之间的差最小。
例如:
var a=[100,99,98,1,2, 3];
var b=[1, 2, 3, 4,5,40];
33.
实现一个挺高级的字符匹配算法:
给一串很长字符串,要求找到符合要求的字符串,例如目的串:123
1******3***2 ,12*****3这些都要找出来
其实就是类似一些和谐系统。。。。。
34.
实现一个队列。
队列的应用场景为:
一个生产者线程将int类型的数入列,一个消费者线程将int类型的数出列
35.
求一个矩阵中最大的二维矩阵(元素和最大).如:
1 2 0 3 4
2 3 4 5 1
1 1 5 3 0
中最大的是:
4 5
5 3
要求:(1)写出算法;(2)分析时间复杂度;(3)用C写出关键代码
第36题-40题(有些题目搜集于CSDN上的网友,已标明):
36.引用自网友:longzuo
谷歌笔试:
n支队伍比赛,分别编号为0,1,2。。。。n-1,已知它们之间的实力对比关系,
存储在一个二维数组w[n][n]中,w[i][j] 的值代表编号为i,j的队伍中更强的一支。
所以w[i][j]=i 或者j,现在给出它们的出场顺序,并存储在数组order[n]中,
比如order[n] = {4,3,5,8,1......},那么第一轮比赛就是 4对3, 5对8。.......
胜者晋级,败者淘汰,同一轮淘汰的所有队伍排名不再细分,即可以随便排,
下一轮由上一轮的胜者按照顺序,再依次两两比,比如可能是4对5,直至出现第一名
编程实现,给出二维数组w,一维数组order 和 用于输出比赛名次的数组result[n],求出result。
37.
有n个长为m+1的字符串,
如果某个字符串的最后m个字符与某个字符串的前m个字符匹配,则两个字符串可以联接,
问这n个字符串最多可以连成一个多长的字符串,如果出现循环,则返回错误。
38.
百度面试:
1.用天平(只能比较,不能称重)从一堆小球中找出其中唯一一个较轻的,使用x次天平,
最多可以从y个小球中找出较轻的那个,求y与x的关系式
2.有一个很大很大的输入流,大到没有存储器可以将其存储下来,而且只输入一次,如何从这个输入
流中随机取得m个记录
3.大量的URL字符串,如何从中去除重复的,优化时间空间复杂度
39.
网易有道笔试:
(1).
求一个二叉树中任意两个节点间的最大距离,
两个节点的距离的定义是 这两个节点间边的个数,
比如某个孩子节点和父节点间的距离是1,和相邻兄弟节点间的距离是2,优化时间空间复杂度。
(2).
求一个有向连通图的割点,割点的定义是,如果除去此节点和与其相关的边,
有向图不再连通,描述算法。
40.百度研发笔试题
引用自:zp155334877
1)设计一个栈结构,满足一下条件:min,push,pop操作的时间复杂度为O(1)。
2)一串首尾相连的珠子(m个),有N种颜色(N<=10),
设计一个算法,取出其中一段,要求包含所有N中颜色,并使长度最短。
并分析时间复杂度与空间复杂度。
3)设计一个系统处理词语搭配问题,比如说 中国 和人民可以搭配,
则中国人民 人民中国都有效。要求:
*系统每秒的查询数量可能上千次;
*词语的数量级为10W;
*每个词至多可以与1W个词搭配
当用户输入中国人民的时候,要求返回与这个搭配词组相关的信息。
接上,第41-60道:
41.求固晶机的晶元查找程序
晶元盘由数目不详的大小一样的晶元组成,晶元并不一定全布满晶元盘,
照相机每次这能匹配一个晶元,如匹配过,则拾取该晶元,
若匹配不过,照相机则按测好的晶元间距移到下一个位置。
求遍历晶元盘的算法 求思路。
42.请修改append函数,利用这个函数实现:
两个非降序链表的并集,1->2->3 和 2->3->5 并为 1->2->3->5
另外只能输出结果,不能修改两个链表的数据。
43.递归和非递归俩种方法实现二叉树的前序遍历。
44.腾讯面试题:
1.设计一个魔方(六面)的程序。
2.有一千万条短信,有重复,以文本文件的形式保存,一行一条,有重复。
请用5分钟时间,找出重复出现最多的前10条。
3.收藏了1万条url,现在给你一条url,如何找出相似的url。(面试官不解释何为相似)
45.雅虎:
1.对于一个整数矩阵,存在一种运算,对矩阵中任意元素加一时,需要其相邻(上下左右)某一个元素也加一,
现给出一正数矩阵,判断其是否能够由一个全零矩阵经过上述运算得到。
2.一个整数数组,长度为n,将其分为m份,使各份的和相等,求m的最大值
比如{3,2,4,3,6} 可以分成{3,2,4,3,6} m=1;
{3,6}{2,4,3} m=2
{3,3}{2,4}{6} m=3 所以m的最大值为3
46.搜狐:
四对括号可以有多少种匹配排列方式?比如两对括号可以有两种:()()和(())
47.创新工场:
求一个数组的最长递减子序列 比如{9,4,3,2,5,4,3,2}的最长递减子序列为{9,5,4,3,2}
48.微软:
一个数组是由一个递减数列左移若干位形成的,比如{4,3,2,1,6,5}
是由{6,5,4,3,2,1}左移两位形成的,在这种数组中查找某一个数。
49.一道看上去很吓人的算法面试题:
如何对n个数进行排序,要求时间复杂度O(n),空间复杂度O(1)
50.网易有道笔试:
1.求一个二叉树中任意两个节点间的最大距离,两个节点的距离的定义是 这两个节点间边的个数,
比如某个孩子节点和父节点间的距离是1,和相邻兄弟节点间的距离是2,优化时间空间复杂度。
2.求一个有向连通图的割点,割点的定义是,
如果除去此节点和与其相关的边,有向图不再连通,描述算法。
51.和为n连续正数序列。
题目:输入一个正数n,输出所有和为n连续正数序列。
例如输入15,由于1+2+3+4+5=4+5+6=7+8=15,所以输出3个连续序列1-5、4-6和7-8。
分析:这是网易的一道面试题。
52.二元树的深度。
题目:输入一棵二元树的根结点,求该树的深度。
从根结点到叶结点依次经过的结点(含根、叶结点)形成树的一条路径,最长路径的长度为树的深度。
例如:输入二元树:
10
/ /
6 14
/ / /
4 12 16
输出该树的深度3。
二元树的结点定义如下:
struct SBinaryTreeNode // a node of the binary tree
{
int m_nValue; // value of node
SBinaryTreeNode *m_pLeft; // left child of node
SBinaryTreeNode *m_pRight; // right child of node
};
分析:这道题本质上还是考查二元树的遍历。
53.字符串的排列。
题目:输入一个字符串,打印出该字符串中字符的所有排列。
例如输入字符串abc,则输出由字符a、b、c所能排列出来的所有字符串abc、acb、bac、bca、cab和cba。
分析:这是一道很好的考查对递归理解的编程题,
因此在过去一年中频繁出现在各大公司的面试、笔试题中。
54.调整数组顺序使奇数位于偶数前面。
题目:输入一个整数数组,调整数组中数字的顺序,使得所有奇数位于数组的前半部分,
所有偶数位于数组的后半部分。要求时间复杂度为O(n)。
55.
题目:类CMyString的声明如下:
class CMyString
{
public:
CMyString(char* pData = NULL);
CMyString(const CMyString& str);
~CMyString(void);
CMyString& operator = (const CMyString& str);
private:
char* m_pData;
};
请实现其赋值运算符的重载函数,要求异常安全,即当对一个对象进行赋值时发生异常,
对象的状态不能改变。
56.最长公共字串。
题目:如果字符串一的所有字符按其在字符串中的顺序出现在另外一个字符串二中,
则字符串一称之为字符串二的子串。
注意,并不要求子串(字符串一)的字符必须连续出现在字符串二中。
请编写一个函数,输入两个字符串,求它们的最长公共子串,并打印出最长公共子串。
例如:输入两个字符串BDCABA和ABCBDAB,字符串BCBA和BDAB都是是它们的最长公共子串,
则输出它们的长度4,并打印任意一个子串。
分析:求最长公共子串(Longest Common Subsequence, LCS)是一道非常经典的动态规划题,
因此一些重视算法的公司像MicroStrategy都把它当作面试题。
July声明:17:02:53 2010-11-09
57.用俩个栈实现队列。
题目:某队列的声明如下:
template<typename T> class CQueue
{
public:
CQueue() {}
~CQueue() {}
void appendTail(const T& node); // append a element to tail
void deleteHead(); // remove a element from head
private:
T> m_stack1;
T> m_stack2;
};
分析:从上面的类的声明中,我们发现在队列中有两个栈。
因此这道题实质上是要求我们用两个栈来实现一个队列。
相信大家对栈和队列的基本性质都非常了解了:栈是一种后入先出的数据容器,
因此对队列进行的插入和删除操作都是在栈顶上进行;队列是一种先入先出的数据容器,
我们总是把新元素插入到队列的尾部,而从队列的头部删除元素。
58.从尾到头输出链表。
题目:输入一个链表的头结点,从尾到头反过来输出每个结点的值。链表结点定义如下:
struct ListNode
{
int m_nKey;
ListNode* m_pNext;
};
分析:这是一道很有意思的面试题。
该题以及它的变体经常出现在各大公司的面试、笔试题中。
59.不能被继承的类。
题目:用C++设计一个不能被继承的类。
分析:这是Adobe公司2007年校园招聘的最新笔试题。
这道题除了考察应聘者的C++基本功底外,还能考察反应能力,是一道很好的题目。
60.在O(1)时间内删除链表结点。
题目:给定链表的头指针和一个结点指针,在O(1)时间删除该结点。链表结点的定义如下:
struct ListNode
{
int m_nKey;
ListNode* m_pNext;
};
函数的声明如下:
void DeleteNode(ListNode* pListHead, ListNode* pToBeDeleted);
分析:这是一道广为流传的Google面试题,能有效考察我们的编程基本功,还能考察我们的反应
速度,更重要的是,还能考察我们对时间复杂度的理解。
----------------------------------------------------------------------------------------------------------------
关于这100道题,我已经上传资源,共享。下载地址:
题目系列:
1.[最新整理公布][汇总II]微软等数据结构+算法面试100题[第1-80题]
http://download.csdn.net/source/2846055
2.[第一部分]精选微软等公司数据结构+算法经典面试100题[1-40题]
http://download.csdn.net/source/2778852
3.[第二部分]精选微软等公司结构+算法面试100题[前41-60题]:
http://download.csdn.net/source/2811703
4.[第1题-60题汇总]微软等数据结构+算法面试100题
http://download.csdn.net/source/2826690
答案系列:
5.[最新答案V0.3版]微软等数据结构+算法面试100题[第21-40题答案]
http://download.csdn.net/source/2832862
6.[答案V0.2版]精选微软数据结构+算法面试100题[前20题]--修正
http://download.csdn.net/source/2813890
//此份答案是针对最初的V0.1版本,进行的校正与修正。
7.[答案V0.1版]精选微软数据结构+算法面试100题[前25题]
http://download.csdn.net/source/2796735
[最新答案V0.3版]微软等数据结构+算法面试100题[第21-40题答案]
http://download.csdn.net/source/2832862
其它整理资源,下载地址:
[第1题-60题汇总]微软等数据结构+算法面试100题
http://download.csdn.net/source/2826690
[答案V0.2版]精选微软数据结构+算法面试100题[前20题]--修正
http://download.csdn.net/source/2813890
//此份答案是针对最初的V0.1版本,进行的校正与修正。
[答案V0.1版]精选微软数据结构+算法面试100题[前25题]
http://download.csdn.net/source/2796735
[第二部分]精选微软等公司结构+算法面试100题[前41-60题]:
http://download.csdn.net/source/2811703
[第一部分]精选微软等公司数据结构+算法经典面试100题[1-40题]
http://download.csdn.net/source/2778852
作者:July。
时间:2010年10月-11月。版权所有,侵权必究。
出处:http://blog.csdn.net/v_JULY_v。
说明:本文原题为:“横空出世,席卷Csdn [评微软等公司数据结构+算法面试100题]”,但后来此微软100题(加上后续的80道,共计180道面试题)已成一系列,被网络上大量疯狂转载,因此特改为上述题目。
-----------------------------------------------------------
入编程这一行之初,便常听人说,要多动手写代码。可要怎么写列?写些什么列?做些什么列?
c语言程序设计100例,太过基础,入门之后,挑战性不够。直接做项目,初学者则需花费大量的时间与精力、且得有一定能力之后。
于是,这份精选微软等公司数据结构+算法面试100题的资料横空出世了:
[推荐] [整理]算法面试:精选微软经典的算法面试100题[前60题](帖子已结) 10.23
http://topic.csdn.net/u/20101023/20/5652ccd7-d510-4c10-9671-307a56006e6d.html。上述帖子已结贴。如果,各位,对100题中任何一题、有任何问题,或想法,请把你的思路、或想法回复到这更新帖子上:
[推荐]横空出世,席卷Csdn:记微软等100题系列数次被荐[100题永久维护地址] 11.26日
http://topic.csdn.net/u/20101126/10/b4f12a00-6280-492f-b785-cb6835a63dc9.html。
======================================================
仅仅一个月, 此帖子4次上csdn bbs首页,3次上csdn首页。总点击率已超过10000(直至现在已被网络上大量疯狂转载,估计已被上十万人看过或见识到)。
在这份资料里,作者不仅大胆的罗列了微软等公司极具代表性的精彩100题,更为重要的是,作者在展示自己思考成果的同时,与一群志同道合的同志,一起思考每一道题,想办法怎样一步步去编写代码,并及时的整理自己的思路、和方案。
这100道题,不仅解决了大量初学者找不到编程素材、练习资料的尴尬,而且更是给你最直接的诱惑:作者随后直接亲自参与做这100题,或自个做,或引用他人方案,一步步带你思考,一步步挖代码给你看。
作者在展示自己和他人思考成果的同时,给他人带来了无比重要的分享,此举颇有开源精神。
不但授之以鱼,而且授之以渔。不但提供给你大量经典的编程素材,而且带给你思考的力量。此等幸运,非有心人莫属。在参与做这100道题的浩荡队伍中,有老师,有学生,有正在工作的上班族,有经验丰富的老者,前微软SDET...等等。如此无私奉献,享受帮助他人的乐趣,思考、分享、追根究底每一道题,此等境界,亦非每一人所有也。
编程就是享受思考。
一句话,盛宴已摆在桌前,敬请享用。
updated:
关于此一百道+后续185道(参见文末),近300道面试题的所有一切详情,请参见,如下:
原题
[珍藏版]微软等数据结构+算法面试全部100题全部出炉[100题首次完整亮相] 1206
http://blog.csdn.net/v_JULY_v/archive/2010/12/06/6057286.aspx
//至此,第1-100题整理完成,如上所示。微软等100题系列V0.1版完成。2010年12月6日。
[汇总II]微软等公司数据结构+算法面试第1-80题[前80题首次集体亮相] 11.27
http://blog.csdn.net/v_JULY_v/archive/2010/11/27/6039896.aspx
帖子
1、2010年10月11日,发表第一篇帖子,
算法面试:精选微软经典的算法面试100题[每周更新] (已结帖)
http://topic.csdn.net/u/20101011/16/2befbfd9-f3e4-41c5-bb31-814e9615832e.html;
2、2010年10月23日,发表第二篇帖子:
[推荐] [整理]算法面试:精选微软经典的算法面试100题[前40题] (4次被推荐,已结帖)
http://topic.csdn.net/u/20101023/20/5652ccd7-d510-4c10-9671-307a56006e6d.html;
3、2010年11月26日,发表第三篇帖子,此微软等100题系列永久维护地址:
[推荐] 横空出世,席卷Csdn:记微软等100题系列数次被荐[100题维护地址] (帖子未结)
http://topic.csdn.net/u/20101126/10/b4f12a00-6280-492f-b785-cb6835a63dc9.html。
资源
题目系列:
- [珍藏版]微软等数据结构+算法面试100题全部出炉 [完整100题下载地址]:http://download.csdn.net/source/2885434
- [最新整理公布][汇总II]微软等数据结构+算法面试100题[第1-80题] :http://download.csdn.net/source/2846055
- [最新答案V0.4版]微软等数据结构+算法面试100题[第41-60题答案] 2011、01、04:http://download.csdn.net/source/2959162
- [答案V0.3版]微软等数据结构+算法面试100题[第21-40题答案]:http://download.csdn.net/source/2832862
- [答案V0.2版]精选微软数据结构+算法面试100题[前20题]--修正:http://download.csdn.net/source/2813890
更多资源,下载地址:
本微软公司面试100题的全部答案日前已经上传资源,所有读者可到此处下载:http://download.csdn.net/detail/v_JULY_v/3685306。2011.10.15。
维护
- 关于本微软等公司数据结构+算法面试100题系列的郑重声明 1202:http://blog.csdn.net/v_JULY_v/archive/2010/12/02/6050133.aspx
- 各位,若关于这100题,有任何问题,可联系我,My e-mail:zhoulei0907@yahoo.cn
- 各位,若对这100题中任何一题,有好的思路、或想法,欢迎回复到下面的帖子上:本微软等100题系列的永久维护,帖子地址,[推荐]横空出世,席卷Csdn:记微软等100题系列数次被荐[100题永久维护地址] 11.26日:http://topic.csdn.net/u/20101126/10/b4f12a00-6280-492f-b785-cb6835a63dc9.html
答案
为了更广泛的与读者就这微软等面试100题交流,也为了更好的获取读者的反馈,
现在,除了可以在我的帖子上,发表思路回复,和下载答案资源外,
我把此微软100题的全部答案直接放到了本博客上,欢迎,所有的广大读者批评指正。
答案V0.2版[第1题-20题答案]
http://blog.csdn.net/v_JULY_v/archive/2011/01/10/6126406.aspx [博文 I]
答案V0.3版[第21-40题答案]
http://blog.csdn.net/v_JULY_v/archive/2011/01/10/6126444.aspx [博文II]
答案V0.4版[第41-60题答案]
http://blog.csdn.net/v_JULY_v/archive/2011/02/01/6171539.aspx [博文III]
有部分答案或参考或借鉴自此博客:http://zhedahht.blog.163.com/。特此声明,十分感谢。
现今,这100题的答案已经全部整理出来了,微软面试100题2010年版全部答案集锦:http://blog.csdn.net/v_july_v/article/details/6870251。2011.10.13。
勘误
- 永久优化:微软技术面试100题第1-10题答案修正与优化,http://blog.csdn.net/v_JULY_v/archive/2011/03/25/6278484.aspx。
- 永久优化:微软技术面试100题第11-20题答案修正与优化,http://blog.csdn.net/v_JULY_v/archive/2011/04/04/6301244.aspx。
后续
- 微软面试100题2010年版全部答案集锦(含下载地址)
- 全新整理:微软、谷歌、百度等公司经典面试100题[第101-160题]
- 全新整理:微软、Google等公司的面试题及解答[第161-170题]
- 十道海量数据处理面试题与十个方法大总结
- 海量数据处理面试题集锦与Bit-map详解
- 教你如何迅速秒杀掉:99%的海量数据处理面试题 (解决海量数据处理问题之六把密匙)
- 九月腾讯,创新工场,淘宝等公司最新面试三十题(第171-200题)
- 十月百度,阿里巴巴,迅雷搜狗最新面试七十题(第201-270题)
- 十月下旬腾讯,网易游戏,百度最新校园招聘笔试题集锦(第271-330题)
- 最新九月百度人搜,阿里巴巴,腾讯华为京东360笔/面试二十题 (2012年度最新九月笔试面试二十题)
艺术
根据本blog里面的180道面试题为题材之一,我专门针对每一道编程题而创作了程序员编程艺术系列,力争将编程过程中所有能体现的到的有关选择合适的数据结构、寻找更高效的算法、编码规范等等内容无私分享,造福天下。详情,请参见:程序员编程艺术系列。目前已经写到了第十章,且将长期写下去。
本编程艺术系列分为三个部分,第一部分、程序设计,主要包括面试题目,ACM题目等各类编程题目的设计与实现,第二部分、算法研究,主要以我之前写的经典算法研究系列为题材扩展深入,第三部分、编码规范,主要阐述有关编程中要注意的规范等问题。ok,一切的详情,请参见:程序员编程艺术系列。
加入
能在网上找到有意义的事情并不多,而如此能帮助到千千万万的初学者,和即将要找工作而参加面试的人的事情更是罕见。希望,你也能参与进我们之中来,一起来做这微软面试187题,一起享受无私分享,开源,思考,共同努力,彼此交流,探讨的诸多无限乐趣:
有很多朋友跟我说,已毕业工作了的一般都不喜欢做面试编程题了。我觉不然,那得看你接受的是什么一种方式,如果抛开面试这个负担,纯粹为编程而编程,享受思考锻炼思维的乐趣,则也可以凝聚成一股开源军,且将声势浩大。如我去年11月发的微软面试贴,如今早已超过1000条回复:http://topic.csdn.net/u/20101126/10/b4f12a00-6280-492f-b785-cb6835a63dc9.html。
版权声明:
1、本人对此微软面试100题系列,包括原题整理,上传资源,帖子,答案,勘误,修正与优化等系列的全部文章或内容,享有全部的版权。任何人转载或引用以上任何资料,一律必须以超链接形式注明出处。
2、未经本人书面许可,严禁任何出版社或个人出版本BLOG内任何内容。否则,永久追究法律责任,永不懈怠(July、二零一零年十月声明)。
微软等数据结构+算法面试100题[最新第61-80题]
精选微软等数据结构+算法面试100题[第61-80题]
--最新整理公布
昨日,11.19,最新整理了,第61-80题,现在公布。
可以这么说,绝大部分的面试题,都是这100道题系列的翻版,
此微软等公司数据结构+算法面试100题系列,是极具代表性的经典面试题。
我曾经暗暗问自己,不知道我是否把面试题基本上都搜集整理尽了,
而当然,对你更重要的是,我自个还提供了答案下载,提供思路,呵。
所以,这份资料+答案,在网上是独一无二的。
闲不多说,接下来,你可以尽情的享用了,朋友。
现在首次公布整理的第61-80题(11.19最新整理公布):
---------------------------------------
[整理I]精选微软等公司数据结构+算法面试100题 [第1-40题] (博文)
http://blog.csdn.net/v_JULY_v/archive/2010/10/27/5968678.aspx
[整理II]精选微软等公司数据结构+算法面试100题 [第41-60题] (博文)
http://blog.csdn.net/v_JULY_v/archive/2010/10/29/5975019.aspx
[汇总I]精选微软等公司数据结构+算法面试100题[第1-60题汇总](博文)
http://blog.csdn.net/v_JULY_v/archive/2010/11/12/6004660.aspx
61.找出数组中两个只出现一次的数字
题目:一个整型数组里除了两个数字之外,其他的数字都出现了两次。
请写程序找出这两个只出现一次的数字。要求时间复杂度是O(n),空间复杂度是O(1)。
分析:这是一道很新颖的关于位运算的面试题。
62.找出链表的第一个公共结点。
题目:两个单向链表,找出它们的第一个公共结点。
链表的结点定义为:
struct ListNode
{
int m_nKey;
ListNode* m_pNext;
};
分析:这是一道微软的面试题。
微软非常喜欢与链表相关的题目,因此在微软的面试题中,链表出现的概率相当高。
63.在字符串中删除特定的字符。
题目:输入两个字符串,从第一字符串中删除第二个字符串中所有的字符。
例如,输入”They are students.”和”aeiou”,则删除之后的第一个字符串变成”Thy r stdnts.”。
分析:这是一道微软面试题。在微软的常见面试题中,与字符串相关的题目占了很大的一部分,
因为写程序操作字符串能很好的反映我们的编程基本功。
64. 寻找丑数。
题目:我们把只包含因子2、3和5的数称作丑数(Ugly Number)。
例如6、8都是丑数,但14不是,因为它包含因子7。习惯上我们把1当做是第一个丑数。
求按从小到大的顺序的第1500个丑数。
分析:这是一道在网络上广为流传的面试题,据说google曾经采用过这道题。
65.输出1到最大的N位数
题目:输入数字n,按顺序输出从1最大的n位10进制数。
比如输入3,则输出1、2、3一直到最大的3位数即999。
分析:这是一道很有意思的题目。看起来很简单,其实里面却有不少的玄机。
66.颠倒栈。
题目:用递归颠倒一个栈。例如输入栈{1, 2, 3, 4, 5},1在栈顶。
颠倒之后的栈为{5, 4, 3, 2, 1},5处在栈顶。
67.俩个闲玩娱乐。
1.扑克牌的顺子
从扑克牌中随机抽5张牌,判断是不是一个顺子,即这5张牌是不是连续的。
2-10为数字本身,A为1,J为11,Q为12,K为13,而大小王可以看成任意数字。
2.n个骰子的点数。
把n个骰子扔在地上,所有骰子朝上一面的点数之和为S。
输入n,打印出S的所有可能的值出现的概率。
68.把数组排成最小的数。
题目:输入一个正整数数组,将它们连接起来排成一个数,输出能排出的所有数字中最小的一个。
例如输入数组{32, 321},则输出这两个能排成的最小数字32132。
请给出解决问题的算法,并证明该算法。
分析:这是09年6月份百度的一道面试题,
从这道题我们可以看出百度对应聘者在算法方面有很高的要求。
69.旋转数组中的最小元素。
题目:把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。
输入一个排好序的数组的一个旋转,输出旋转数组的最小元素。
例如数组{3, 4, 5, 1, 2}为{1, 2, 3, 4, 5}的一个旋转,该数组的最小值为1。
分析:这道题最直观的解法并不难。从头到尾遍历数组一次,就能找出最小的元素,
时间复杂度显然是O(N)。但这个思路没有利用输入数组的特性,我们应该能找到更好的解法。
70.给出一个函数来输出一个字符串的所有排列。
分析:简单的回溯就可以实现了。当然排列的产生也有很多种算法,去看看组合数学,
还有逆序生成排列和一些不需要递归生成排列的方法。
印象中Knuth的<TAOCP>第一卷里面深入讲了排列的生成。
这些算法的理解需要一定的数学功底,
也需要一定的灵感,有兴趣最好看看。
71.数值的整数次方。
题目:实现函数double Power(double base, int exponent),求base的exponent次方。
不需要考虑溢出。
分析:这是一道看起来很简单的问题。可能有不少的人在看到题目后30秒写出如下的代码:
double Power(double base, int exponent)
{
double result = 1.0;
for(int i = 1; i <= exponent; ++i)
result *= base;
return result;
}
72.
题目:设计一个类,我们只能生成该类的一个实例。
分析:只能生成一个实例的类是实现了Singleton模式的类型。
73.对策字符串的最大长度。
题目:输入一个字符串,输出该字符串中对称的子字符串的最大长度。
比如输入字符串“google”,由于该字符串里最长的对称子字符串是“goog”,因此输出4。
分析:可能很多人都写过判断一个字符串是不是对称的函数,这个题目可以看成是该函数的加强版。
74.数组中超过出现次数超过一半的数字
题目:数组中有一个数字出现的次数超过了数组长度的一半,找出这个数字。
分析:这是一道广为流传的面试题,包括百度、微软和Google在内的多家公司
都曾经采用过这个题目。要几十分钟的时间里很好地解答这道题,除了较好的编程能力之外,
还需要较快的反应和较强的逻辑思维能力。
75.二叉树两个结点的最低共同父结点
题目:二叉树的结点定义如下:
struct TreeNode
{
int m_nvalue;
TreeNode* m_pLeft;
TreeNode* m_pRight;
};
输入二叉树中的两个结点,输出这两个结点在数中最低的共同父结点。
分析:求数中两个结点的最低共同结点是面试中经常出现的一个问题。这个问题至少有两个变种。
76.复杂链表的复制
题目:有一个复杂链表,其结点除了有一个m_pNext指针指向下一个结点外,
还有一个m_pSibling指向链表中的任一结点或者NULL。其结点的C++定义如下:
struct ComplexNode
{
int m_nValue;
ComplexNode* m_pNext;
ComplexNode* m_pSibling;
};
下图是一个含有5个结点的该类型复杂链表。
图中实线箭头表示m_pNext指针,虚线箭头表示m_pSibling指针。
为简单起见,指向NULL的指针没有画出。
请完成函数ComplexNode* Clone(ComplexNode* pHead),以复制一个复杂链表。
//图,接下来,自会补上。July、11.19.
分析:在常见的数据结构上稍加变化,这是一种很新颖的面试题。
要在不到一个小时的时间里解决这种类型的题目,
我们需要较快的反应能力,对数据结构透彻的理解以及扎实的编程功底。
77.关于链表问题的面试题目如下:
题一、 给定单链表,检测是否有环。
使用两个指针p1,p2从链表头开始遍历,p1每次前进一步,p2每次前进两步。
如果p2到达链表尾部,说明无环,否则p1、p2必然会在某个时刻相遇(p1==p2),从而检测到链表中有环。
题二、 给定两个单链表(head1, head2),检测两个链表是否有交点,如果有返回第一个交点。
如果head1==head2,那么显然相交,直接返回head1。
否则,分别从head1,head2开始遍历两个链表获得其长度len1与len2,假设len1>=len2,
那么指针p1由head1开始向后移动len1-len2步,指针p2=head2,
下面p1、p2每次向后前进一步并比较p1p2是否相等,如果相等即返回该结点,
否则说明两个链表没有交点。
题三、 给定单链表(head),如果有环的话请返回从头结点进入环的第一个节点。
运用题一,我们可以检查链表中是否有环。
如果有环,那么p1p2重合点p必然在环中。从p点断开环,方法为:p1=p, p2=p->next,
p->next=NULL。此时,原单链表可以看作两条单链表,一条从head开始,另一条从p2开始,
于是运用题二的方法,我们找到它们的第一个交点即为所求。
题四、只给定单链表中某个结点p(并非最后一个结点,即p->next!=NULL)指针,删除该结点。
办法很简单,首先是放p中数据,然后将p->next的数据copy入p中,接下来删除p->next即可。
题五、只给定单链表中某个结点p(非空结点),在p前面插入一个结点。
办法与前者类似,首先分配一个结点q,将q插入在p后,
接下来将p中的数据copy入q中,然后再将要插入的数据记录在p中。
78.链表和数组的区别在哪里?
分析:主要在基本概念上的理解。
但是最好能考虑的全面一点,现在公司招人的竞争可能就在细节上产生,
谁比较仔细,谁获胜的机会就大。
79.
1.编写实现链表排序的一种算法。说明为什么你会选择用这样的方法?
2.编写实现数组排序的一种算法。说明为什么你会选择用这样的方法?
3.请编写能直接实现strstr()函数功能的代码。
80.阿里巴巴一道笔试题
引自baihacker
问题描述:
12个高矮不同的人,排成两排,每排必须是从矮到高排列,而且第二排比对应的第一排的人高,问排列方式有多少种?
这个笔试题,很YD,因为把某个递归关系隐藏得很深.
//第81-100题正在整理中。
---------------------------------------------------------------------------------------
整理资源下载地址:
题目系列:
1.[最新整理公布][汇总II]微软等数据结构+算法面试100题[第1-80题]
http://download.csdn.net/source/2846055
2.[第一部分]精选微软等公司数据结构+算法经典面试100题[1-40题]
http://download.csdn.net/source/2778852
3.[第二部分]精选微软等公司结构+算法面试100题[前41-60题]:
http://download.csdn.net/source/2811703
4.[第1题-60题汇总]微软等数据结构+算法面试100题
http://download.csdn.net/source/2826690
答案系列:
5.[最新答案V0.3版]微软等数据结构+算法面试100题[第21-40题答案]
http://download.csdn.net/source/2832862
6.[答案V0.2版]精选微软数据结构+算法面试100题[前20题]--修正
http://download.csdn.net/source/2813890
//此份答案是针对最初的V0.1版本,进行的校正与修正。
7.[答案V0.1版]精选微软数据结构+算法面试100题[前25题]
http://download.csdn.net/source/2796735
更多资源,下载地址:
http://v_july_v.download.csdn.net/
谢谢。
---------------------------------------
各位,我已经针对本100题, 开了一帖,作为本微软等100题系列的永久维护地址。
真诚欢迎,各位,前去帖子上,写下对这100道题中任何一题的思路或想法。
帖子地址:
微软等公司数据结构+算法面试第1-80题[前80题首次集体亮相]
[整理III]微软等公司数据结构+算法面试第1-80题汇总
---首次一次性汇总公布
由于这些题,实在太火了。所以,应广大网友建议要求,在此把之前已整理公布的前80题,
现在,一次性分享出来。此也算是前80题第一次集体亮相。
此些题,已有上万人,看到或见识到,若私自据为己有,必定为有知之人识破,付出代价。
所以,作者声明:
本人July对以上所有任何内容和资料享有版权,转载请注明作者本人July出处。
向你的厚道致敬。谢谢。
2010年11月27日。
----------------------------------------------------------------------------------------------------------------
1.把二元查找树转变成排序的双向链表
题目:
输入一棵二元查找树,将该二元查找树转换成一个排序的双向链表。
要求不能创建任何新的结点,只调整指针的指向。
10
/ /
6 14
/ / / /
4 8 12 16
转换成双向链表
4=6=8=10=12=14=16。
首先我们定义的二元查找树 节点的数据结构如下:
struct BSTreeNode
{
int m_nValue; // value of node
BSTreeNode *m_pLeft; // left child of node
BSTreeNode *m_pRight; // right child of node
};
2.设计包含min函数的栈。
定义栈的数据结构,要求添加一个min函数,能够得到栈的最小元素。
要求函数min、push以及pop的时间复杂度都是O(1)。
3.求子数组的最大和
题目:
输入一个整形数组,数组里有正数也有负数。
数组中连续的一个或多个整数组成一个子数组,每个子数组都有一个和。
求所有子数组的和的最大值。要求时间复杂度为O(n)。
例如输入的数组为1, -2, 3, 10, -4, 7, 2, -5,和最大的子数组为3, 10, -4, 7, 2,
因此输出为该子数组的和18。
4.在二元树中找出和为某一值的所有路径
题目:输入一个整数和一棵二元树。
从树的根结点开始往下访问一直到叶结点所经过的所有结点形成一条路径。
打印出和与输入整数相等的所有路径。
例如 输入整数22和如下二元树
10
/ /
5 12
/ /
4 7
则打印出两条路径:10, 12和10, 5, 7。
二元树节点的数据结构定义为:
struct BinaryTreeNode // a node in the binary tree
{
int m_nValue; // value of node
BinaryTreeNode *m_pLeft; // left child of node
BinaryTreeNode *m_pRight; // right child of node
};
5.查找最小的k个元素
题目:输入n个整数,输出其中最小的k个。
例如输入1,2,3,4,5,6,7和8这8个数字,则最小的4个数字为1,2,3和4。
第6题
腾讯面试题:
给你10分钟时间,根据上排给出十个数,在其下排填出对应的十个数
要求下排每个数都是先前上排那十个数在下排出现的次数。
上排的十个数如下:
【0,1,2,3,4,5,6,7,8,9】
举一个例子,
数值: 0,1,2,3,4,5,6,7,8,9
分配: 6,2,1,0,0,0,1,0,0,0
0在下排出现了6次,1在下排出现了2次,
2在下排出现了1次,3在下排出现了0次....
以此类推..
第7题
微软亚院之编程判断俩个链表是否相交
给出俩个单向链表的头指针,比如h1,h2,判断这俩个链表是否相交。
为了简化问题,我们假设俩个链表均不带环。
问题扩展:
1.如果链表可能有环列?
2.如果需要求出俩个链表相交的第一个节点列?
第8题
此贴选一些 比较怪的题,,由于其中题目本身与算法关系不大,仅考考思维。特此并作一题。
1.有两个房间,一间房里有三盏灯,另一间房有控制着三盏灯的三个开关,
这两个房间是 分割开的,从一间里不能看到另一间的情况。
现在要求受训者分别进这两房间一次,然后判断出这三盏灯分别是由哪个开关控制的。
有什么办法呢?
2.你让一些人为你工作了七天,你要用一根金条作为报酬。金条被分成七小块,每天给出一块。
如果你只能将金条切割两次,你怎样分给这些工人?
3. ★用一种算法来颠倒一个链接表的顺序。现在在不用递归式的情况下做一遍。
★用一种算法在一个循环的链接表里插入一个节点,但不得穿越链接表。
★用一种算法整理一个数组。你为什么选择这种方法?
★用一种算法使通用字符串相匹配。
★颠倒一个字符串。优化速度。优化空间。
★颠倒一个句子中的词的顺序,比如将“我叫克丽丝”转换为“克丽丝叫我”,
实现速度最快,移动最少。
★找到一个子字符串。优化速度。优化空间。
★比较两个字符串,用O(n)时间和恒量空间。
★假设你有一个用1001个整数组成的数组,这些整数是任意排列的,但是你知道所有的整数都在1到1000(包括1000)之间。此外,除一个数字出现两次外,其他所有数字只出现一次。假设你只能对这个数组做一次处理,用一种算法找出重复的那个数字。如果你在运算中使用了辅助的存储方式,那么你能找到不用这种方式的算法吗?
★不用乘法或加法增加8倍。现在用同样的方法增加7倍。
第9题
判断整数序列是不是二元查找树的后序遍历结果
题目:输入一个整数数组,判断该数组是不是某二元查找树的后序遍历的结果。
如果是返回true,否则返回false。
例如输入5、7、6、9、11、10、8,由于这一整数序列是如下树的后序遍历结果:
8
/ /
6 10
/ / / /
5 7 9 11
因此返回true。
如果输入7、4、6、5,没有哪棵树的后序遍历的结果是这个序列,因此返回false。
第10题
翻转句子中单词的顺序。
题目:输入一个英文句子,翻转句子中单词的顺序,但单词内字符的顺序不变。
句子中单词以空格符隔开。为简单起见,标点符号和普通字母一样处理。
例如输入“I am a student.”,则输出“student. a am I”。
第11题
求二叉树中节点的最大距离...
如果我们把二叉树看成一个图,父子节点之间的连线看成是双向的,
我们姑且定义"距离"为两节点之间边的个数。
写一个程序,
求一棵二叉树中相距最远的两个节点之间的距离。
第12题
题目:求1+2+…+n,
要求不能使用乘除法、for、while、if、else、switch、case等关键字以及条件判断语句(A?B:C)。
第13题:
题目:输入一个单向链表,输出该链表中倒数第k个结点。链表的倒数第0个结点为链表的尾指针。
链表结点定义如下:
struct ListNode
{
int m_nKey;
ListNode* m_pNext;
};
第14题:
题目:输入一个已经按升序排序过的数组和一个数字,
在数组中查找两个数,使得它们的和正好是输入的那个数字。
要求时间复杂度是O(n)。如果有多对数字的和等于输入的数字,输出任意一对即可。
例如输入数组1、2、4、7、11、15和数字15。由于4+11=15,因此输出4和11。
第15题:
题目:输入一颗二元查找树,将该树转换为它的镜像,
即在转换后的二元查找树中,左子树的结点都大于右子树的结点。
用递归和循环两种方法完成树的镜像转换。
例如输入:
8
/ /
6 10
// //
5 7 9 11
输出:
8
/ /
10 6
// //
11 9 7 5
定义二元查找树的结点为:
struct BSTreeNode // a node in the binary search tree (BST)
{
int m_nValue; // value of node
BSTreeNode *m_pLeft; // left child of node
BSTreeNode *m_pRight; // right child of node
};
第16题:
题目(微软):
输入一颗二元树,从上往下按层打印树的每个结点,同一层中按照从左往右的顺序打印。
例如输入
8
/ /
6 10
/ / / /
5 7 9 11
输出8 6 10 5 7 9 11。
第17题:
题目:在一个字符串中找到第一个只出现一次的字符。如输入abaccdeff,则输出b。
分析:这道题是2006年google的一道笔试题。
第18题:
题目:n个数字(0,1,…,n-1)形成一个圆圈,从数字0开始,
每次从这个圆圈中删除第m个数字(第一个为当前数字本身,第二个为当前数字的下一个数字)。
当一个数字删除后,从被删除数字的下一个继续删除第m个数字。
求出在这个圆圈中剩下的最后一个数字。
July:我想,这个题目,不少人已经 见识过了。
第19题:
题目:定义Fibonacci数列如下:
/ 0 n=0
f(n)= 1 n=1
/ f(n-1)+f(n-2) n=2
输入n,用最快的方法求该数列的第n项。
分析:在很多C语言教科书中讲到递归函数的时候,都会用Fibonacci作为例子。
因此很多程序员对这道题的递归解法非常熟悉,但....呵呵,你知道的。。
第20题:
题目:输入一个表示整数的字符串,把该字符串转换成整数并输出。
例如输入字符串"345",则输出整数345。
第21题
2010年中兴面试题
编程求解:
输入两个整数 n 和 m,从数列1,2,3.......n 中 随意取几个数,
使其和等于 m ,要求将其中所有的可能组合列出来.
第22题:
有4张红色的牌和4张蓝色的牌,主持人先拿任意两张,再分别在A、B、C三人额头上贴任意两张牌,
A、B、C三人都可以看见其余两人额头上的牌,看完后让他们猜自己额头上是什么颜色的牌,
A说不知道,B说不知道,C说不知道,然后A说知道了。
请教如何推理,A是怎么知道的。
如果用程序,又怎么实现呢?
第23题:
用最简单,最快速的方法计算出下面这个圆形是否和正方形相交。"
3D坐标系 原点(0.0,0.0,0.0)
圆形:
半径r = 3.0
圆心o = (*.*, 0.0, *.*)
正方形:
4个角坐标;
1:(*.*, 0.0, *.*)
2:(*.*, 0.0, *.*)
3:(*.*, 0.0, *.*)
4:(*.*, 0.0, *.*)
第24题:
链表操作,
(1).单链表就地逆置,
(2)合并链表
第25题:
写一个函数,它的原形是int continumax(char *outputstr,char *intputstr)
功能:
在字符串中找出连续最长的数字串,并把这个串的长度返回,
并把这个最长数字串付给其中一个函数参数outputstr所指内存。
例如:"abcd12345ed125ss123456789"的首地址传给intputstr后,函数将返回9,
outputstr所指的值为123456789
26.左旋转字符串
题目:
定义字符串的左旋转操作:把字符串前面的若干个字符移动到字符串的尾部。
如把字符串abcdef左旋转2位得到字符串cdefab。请实现字符串左旋转的函数。
要求时间对长度为n的字符串操作的复杂度为O(n),辅助内存为O(1)。
27.跳台阶问题
题目:一个台阶总共有n级,如果一次可以跳1级,也可以跳2级。
求总共有多少总跳法,并分析算法的时间复杂度。
这道题最近经常出现,包括MicroStrategy等比较重视算法的公司
都曾先后选用过个这道题作为面试题或者笔试题。
28.整数的二进制表示中1的个数
题目:输入一个整数,求该整数的二进制表达中有多少个1。
例如输入10,由于其二进制表示为1010,有两个1,因此输出2。
分析:
这是一道很基本的考查位运算的面试题。
包括微软在内的很多公司都曾采用过这道题。
29.栈的push、pop序列
题目:输入两个整数序列。其中一个序列表示栈的push顺序,
判断另一个序列有没有可能是对应的pop顺序。
为了简单起见,我们假设push序列的任意两个整数都是不相等的。
比如输入的push序列是1、2、3、4、5,那么4、5、3、2、1就有可能是一个pop系列。
因为可以有如下的push和pop序列:
push 1,push 2,push 3,push 4,pop,push 5,pop,pop,pop,pop,
这样得到的pop序列就是4、5、3、2、1。
但序列4、3、5、1、2就不可能是push序列1、2、3、4、5的pop序列。
30.在从1到n的正数中1出现的次数
题目:输入一个整数n,求从1到n这n个整数的十进制表示中1出现的次数。
例如输入12,从1到12这些整数中包含1 的数字有1,10,11和12,1一共出现了5次。
分析:这是一道广为流传的google面试题。
31.华为面试题:
一类似于蜂窝的结构的图,进行搜索最短路径(要求5分钟)
32.
有两个序列a,b,大小都为n,序列元素的值任意整数,无序;
要求:通过交换a,b中的元素,使[序列a元素的和]与[序列b元素的和]之间的差最小。
例如:
var a=[100,99,98,1,2, 3];
var b=[1, 2, 3, 4,5,40];
33.
实现一个挺高级的字符匹配算法:
给一串很长字符串,要求找到符合要求的字符串,例如目的串:123
1******3***2 ,12*****3这些都要找出来
其实就是类似一些和谐系统。。。。。
34.
实现一个队列。
队列的应用场景为:
一个生产者线程将int类型的数入列,一个消费者线程将int类型的数出列
35.
求一个矩阵中最大的二维矩阵(元素和最大).如:
1 2 0 3 4
2 3 4 5 1
1 1 5 3 0
中最大的是:
4 5
5 3
要求:(1)写出算法;(2)分析时间复杂度;(3)用C写出关键代码
第36题-40题(有些题目搜集于CSDN上的网友,已标明):
36.引用自网友:longzuo
谷歌笔试:
n支队伍比赛,分别编号为0,1,2。。。。n-1,已知它们之间的实力对比关系,
存储在一个二维数组w[n][n]中,w[i][j] 的值代表编号为i,j的队伍中更强的一支。
所以w[i][j]=i 或者j,现在给出它们的出场顺序,并存储在数组order[n]中,
比如order[n] = {4,3,5,8,1......},那么第一轮比赛就是 4对3, 5对8。.......
胜者晋级,败者淘汰,同一轮淘汰的所有队伍排名不再细分,即可以随便排,
下一轮由上一轮的胜者按照顺序,再依次两两比,比如可能是4对5,直至出现第一名
编程实现,给出二维数组w,一维数组order 和 用于输出比赛名次的数组result[n],
求出result。
37.
有n个长为m+1的字符串,
如果某个字符串的最后m个字符与某个字符串的前m个字符匹配,则两个字符串可以联接,
问这n个字符串最多可以连成一个多长的字符串,如果出现循环,则返回错误。
38.
百度面试:
1.用天平(只能比较,不能称重)从一堆小球中找出其中唯一一个较轻的,使用x次天平,
最多可以从y个小球中找出较轻的那个,求y与x的关系式。
2.有一个很大很大的输入流,大到没有存储器可以将其存储下来,
而且只输入一次,如何从这个输入流中随机取得m个记录。
3.大量的URL字符串,如何从中去除重复的,优化时间空间复杂度
39.
网易有道笔试:
(1).
求一个二叉树中任意两个节点间的最大距离,
两个节点的距离的定义是 这两个节点间边的个数,
比如某个孩子节点和父节点间的距离是1,和相邻兄弟节点间的距离是2,优化时间空间复杂度。
(2).
求一个有向连通图的割点,割点的定义是,如果除去此节点和与其相关的边,
有向图不再连通,描述算法。
40.百度研发笔试题
引用自:zp155334877
1)设计一个栈结构,满足一下条件:min,push,pop操作的时间复杂度为O(1)。
2)一串首尾相连的珠子(m个),有N种颜色(N<=10),
设计一个算法,取出其中一段,要求包含所有N中颜色,并使长度最短。
并分析时间复杂度与空间复杂度。
3)设计一个系统处理词语搭配问题,比如说 中国 和人民可以搭配,
则中国人民 人民中国都有效。要求:
*系统每秒的查询数量可能上千次;
*词语的数量级为10W;
*每个词至多可以与1W个词搭配
当用户输入中国人民的时候,要求返回与这个搭配词组相关的信息。
41.求固晶机的晶元查找程序
晶元盘由数目不详的大小一样的晶元组成,晶元并不一定全布满晶元盘,
照相机每次这能匹配一个晶元,如匹配过,则拾取该晶元,
若匹配不过,照相机则按测好的晶元间距移到下一个位置。
求遍历晶元盘的算法 求思路。
42.请修改append函数,利用这个函数实现:
两个非降序链表的并集,1->2->3 和 2->3->5 并为 1->2->3->5
另外只能输出结果,不能修改两个链表的数据。
43.递归和非递归俩种方法实现二叉树的前序遍历。
44.腾讯面试题:
1.设计一个魔方(六面)的程序。
2.有一千万条短信,有重复,以文本文件的形式保存,一行一条,有重复。
请用5分钟时间,找出重复出现最多的前10条。
3.收藏了1万条url,现在给你一条url,如何找出相似的url。(面试官不解释何为相似)
45.雅虎:
1.对于一个整数矩阵,存在一种运算,对矩阵中任意元素加一时,需要其相邻(上下左右)
某一个元素也加一,现给出一正数矩阵,判断其是否能够由一个全零矩阵经过上述运算得到。
2.一个整数数组,长度为n,将其分为m份,使各份的和相等,求m的最大值
比如{3,2,4,3,6} 可以分成{3,2,4,3,6} m=1;
{3,6}{2,4,3} m=2
{3,3}{2,4}{6} m=3 所以m的最大值为3
46.搜狐:
四对括号可以有多少种匹配排列方式?比如两对括号可以有两种:()()和(())
47.创新工场:
求一个数组的最长递减子序列 比如{9,4,3,2,5,4,3,2}的最长递减子序列为{9,5,4,3,2}
48.微软:
一个数组是由一个递减数列左移若干位形成的,比如{4,3,2,1,6,5}
是由{6,5,4,3,2,1}左移两位形成的,在这种数组中查找某一个数。
49.一道看上去很吓人的算法面试题:
如何对n个数进行排序,要求时间复杂度O(n),空间复杂度O(1)
50.网易有道笔试:
1.求一个二叉树中任意两个节点间的最大距离,两个节点的距离的定义是 这两个节点间边的个数,
比如某个孩子节点和父节点间的距离是1,和相邻兄弟节点间的距离是2,优化时间空间复杂度。
2.求一个有向连通图的割点,割点的定义是,
如果除去此节点和与其相关的边,有向图不再连通,描述算法。
-------------------------------------------------------------------
51.和为n连续正数序列。
题目:输入一个正数n,输出所有和为n连续正数序列。
例如输入15,由于1+2+3+4+5=4+5+6=7+8=15,所以输出3个连续序列1-5、4-6和7-8。
分析:这是网易的一道面试题。
52.二元树的深度。
题目:输入一棵二元树的根结点,求该树的深度。
从根结点到叶结点依次经过的结点(含根、叶结点)形成树的一条路径,最长路径的长度为树的深度。
例如:输入二元树:
10
/ /
6 14
/ / /
4 12 16
输出该树的深度3。
二元树的结点定义如下:
struct SBinaryTreeNode // a node of the binary tree
{
int m_nValue; // value of node
SBinaryTreeNode *m_pLeft; // left child of node
SBinaryTreeNode *m_pRight; // right child of node
};
分析:这道题本质上还是考查二元树的遍历。
53.字符串的排列。
题目:输入一个字符串,打印出该字符串中字符的所有排列。
例如输入字符串abc,则输出由字符a、b、c所能排列出来的所有字符串
abc、acb、bac、bca、cab和cba。
分析:这是一道很好的考查对递归理解的编程题,
因此在过去一年中频繁出现在各大公司的面试、笔试题中。
54.调整数组顺序使奇数位于偶数前面。
题目:输入一个整数数组,调整数组中数字的顺序,使得所有奇数位于数组的前半部分,
所有偶数位于数组的后半部分。要求时间复杂度为O(n)。
55.
题目:类CMyString的声明如下:
class CMyString
{
public:
CMyString(char* pData = NULL);
CMyString(const CMyString& str);
~CMyString(void);
CMyString& operator = (const CMyString& str);
private:
char* m_pData;
};
请实现其赋值运算符的重载函数,要求异常安全,即当对一个对象进行赋值时发生异常,对象的状态不能改变。
56.最长公共字串。
题目:如果字符串一的所有字符按其在字符串中的顺序出现在另外一个字符串二中,
则字符串一称之为字符串二的子串。
注意,并不要求子串(字符串一)的字符必须连续出现在字符串二中。
请编写一个函数,输入两个字符串,求它们的最长公共子串,并打印出最长公共子串。
例如:输入两个字符串BDCABA和ABCBDAB,字符串BCBA和BDAB都是是它们的最长公共子串,
则输出它们的长度4,并打印任意一个子串。
分析:求最长公共子串(Longest Common Subsequence, LCS)是一道非常经典的动态规划题,
因此一些重视算法的公司像MicroStrategy都把它当作面试题。
57.用俩个栈实现队列。
题目:某队列的声明如下:
template<typename T> class CQueue
{
public:
CQueue() {}
~CQueue() {}
void appendTail(const T& node); // append a element to tail
void deleteHead(); // remove a element from head
private:
T> m_stack1;
T> m_stack2;
};
分析:从上面的类的声明中,我们发现在队列中有两个栈。
因此这道题实质上是要求我们用两个栈来实现一个队列。
相信大家对栈和队列的基本性质都非常了解了:栈是一种后入先出的数据容器,
因此对队列进行的插入和删除操作都是在栈顶上进行;队列是一种先入先出的数据容器,
我们总是把新元素插入到队列的尾部,而从队列的头部删除元素。
58.从尾到头输出链表。
题目:输入一个链表的头结点,从尾到头反过来输出每个结点的值。链表结点定义如下:
struct ListNode
{
int m_nKey;
ListNode* m_pNext;
};
分析:这是一道很有意思的面试题。
该题以及它的变体经常出现在各大公司的面试、笔试题中。
59.不能被继承的类。
题目:用C++设计一个不能被继承的类。
分析:这是Adobe公司2007年校园招聘的最新笔试题。
这道题除了考察应聘者的C++基本功底外,还能考察反应能力,是一道很好的题目。
60.在O(1)时间内删除链表结点。
题目:给定链表的头指针和一个结点指针,在O(1)时间删除该结点。链表结点的定义如下:
struct ListNode
{
int m_nKey;
ListNode* m_pNext;
};
函数的声明如下:
void DeleteNode(ListNode* pListHead, ListNode* pToBeDeleted);
分析:这是一道广为流传的Google面试题,能有效考察我们的编程基本功,还能考察我们的反应速度,
更重要的是,还能考察我们对时间复杂度的理解。
-------------------------------------------------------------------------
61.找出数组中两个只出现一次的数字
题目:一个整型数组里除了两个数字之外,其他的数字都出现了两次。
请写程序找出这两个只出现一次的数字。要求时间复杂度是O(n),空间复杂度是O(1)。
分析:这是一道很新颖的关于位运算的面试题。
62.找出链表的第一个公共结点。
题目:两个单向链表,找出它们的第一个公共结点。
链表的结点定义为:
struct ListNode
{
int m_nKey;
ListNode* m_pNext;
};
分析:这是一道微软的面试题。微软非常喜欢与链表相关的题目,
因此在微软的面试题中,链表出现的概率相当高。
63.在字符串中删除特定的字符。
题目:输入两个字符串,从第一字符串中删除第二个字符串中所有的字符。例如,输入”They are students.”和”aeiou”,
则删除之后的第一个字符串变成”Thy r stdnts.”。
分析:这是一道微软面试题。在微软的常见面试题中,与字符串相关的题目占了很大的一部分,
因为写程序操作字符串能很好的反映我们的编程基本功。
64. 寻找丑数。
题目:我们把只包含因子2、3和5的数称作丑数(Ugly Number)。例如6、8都是丑数,
但14不是,因为它包含因子7。习惯上我们把1当做是第一个丑数。
求按从小到大的顺序的第1500个丑数。
分析:这是一道在网络上广为流传的面试题,据说google曾经采用过这道题。
65.输出1到最大的N位数
题目:输入数字n,按顺序输出从1最大的n位10进制数。比如输入3,
则输出1、2、3一直到最大的3位数即999。
分析:这是一道很有意思的题目。看起来很简单,其实里面却有不少的玄机。
66.颠倒栈。
题目:用递归颠倒一个栈。例如输入栈{1, 2, 3, 4, 5},1在栈顶。
颠倒之后的栈为{5, 4, 3, 2, 1},5处在栈顶。
67.俩个闲玩娱乐。
1.扑克牌的顺子
从扑克牌中随机抽5张牌,判断是不是一个顺子,即这5张牌是不是连续的。
2-10为数字本身,A为1,J为11,Q为12,K为13,而大小王可以看成任意数字。
2.n个骰子的点数。
把n个骰子扔在地上,所有骰子朝上一面的点数之和为S。输入n,
打印出S的所有可能的值出现的概率。
68.把数组排成最小的数。
题目:输入一个正整数数组,将它们连接起来排成一个数,输出能排出的所有数字中最小的一个。
例如输入数组{32, 321},则输出这两个能排成的最小数字32132。
请给出解决问题的算法,并证明该算法。
分析:这是09年6月份百度的一道面试题,
从这道题我们可以看出百度对应聘者在算法方面有很高的要求。
69.旋转数组中的最小元素。
题目:把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。输入一个排好序的数组的一个旋转,
输出旋转数组的最小元素。例如数组{3, 4, 5, 1, 2}为{1, 2, 3, 4, 5}的一个旋转,该数组的最小值为1。
分析:这道题最直观的解法并不难。从头到尾遍历数组一次,就能找出最小的元素,
时间复杂度显然是O(N)。但这个思路没有利用输入数组的特性,我们应该能找到更好的解法。
70.给出一个函数来输出一个字符串的所有排列。
ANSWER 简单的回溯就可以实现了。当然排列的产生也有很多种算法,去看看组合数学,
还有逆序生成排列和一些不需要递归生成排列的方法。
印象中Knuth的<TAOCP>第一卷里面深入讲了排列的生成。这些算法的理解需要一定的数学功底,
也需要一定的灵感,有兴趣最好看看。
71.数值的整数次方。
题目:实现函数double Power(double base, int exponent),求base的exponent次方。
不需要考虑溢出。
分析:这是一道看起来很简单的问题。可能有不少的人在看到题目后30秒写出如下的代码:
double Power(double base, int exponent)
{
double result = 1.0;
for(int i = 1; i <= exponent; ++i)
result *= base;
return result;
}
72.
题目:设计一个类,我们只能生成该类的一个实例。
分析:只能生成一个实例的类是实现了Singleton模式的类型。
73.对策字符串的最大长度。
题目:输入一个字符串,输出该字符串中对称的子字符串的最大长度。
比如输入字符串“google”,由于该字符串里最长的对称子字符串是“goog”,因此输出4。
分析:可能很多人都写过判断一个字符串是不是对称的函数,这个题目可以看成是该函数的加强版。
74.数组中超过出现次数超过一半的数字
题目:数组中有一个数字出现的次数超过了数组长度的一半,找出这个数字。
分析:这是一道广为流传的面试题,包括百度、微软和Google在内的多家公司都
曾经采用过这个题目。要几十分钟的时间里很好地解答这道题,
除了较好的编程能力之外,还需要较快的反应和较强的逻辑思维能力。
75.二叉树两个结点的最低共同父结点
题目:二叉树的结点定义如下:
struct TreeNode
{
int m_nvalue;
TreeNode* m_pLeft;
TreeNode* m_pRight;
};
输入二叉树中的两个结点,输出这两个结点在数中最低的共同父结点。
分析:求数中两个结点的最低共同结点是面试中经常出现的一个问题。这个问题至少有两个变种。
76.复杂链表的复制
题目:有一个复杂链表,其结点除了有一个m_pNext指针指向下一个结点外,
还有一个m_pSibling指向链表中的任一结点或者NULL。其结点的C++定义如下:
struct ComplexNode
{
int m_nValue;
ComplexNode* m_pNext;
ComplexNode* m_pSibling;
};
下图是一个含有5个结点的该类型复杂链表。
图中实线箭头表示m_pNext指针,虚线箭头表示m_pSibling指针。为简单起见,
指向NULL的指针没有画出。
请完成函数ComplexNode* Clone(ComplexNode* pHead),以复制一个复杂链表。
分析:在常见的数据结构上稍加变化,这是一种很新颖的面试题。
要在不到一个小时的时间里解决这种类型的题目,我们需要较快的反应能力,
对数据结构透彻的理解以及扎实的编程功底。
77.关于链表问题的面试题目如下:
1.给定单链表,检测是否有环。
使用两个指针p1,p2从链表头开始遍历,p1每次前进一步,p2每次前进两步。如果p2到达链表尾部,
说明无环,否则p1、p2必然会在某个时刻相遇(p1==p2),从而检测到链表中有环。
2.给定两个单链表(head1, head2),检测两个链表是否有交点,如果有返回第一个交点。
如果head1==head2,那么显然相交,直接返回head1。
否则,分别从head1,head2开始遍历两个链表获得其长度len1与len2,假设len1>=len2,
那么指针p1由head1开始向后移动len1-len2步,指针p2=head2,
下面p1、p2每次向后前进一步并比较p1p2是否相等,如果相等即返回该结点,
否则说明两个链表没有交点。
3.给定单链表(head),如果有环的话请返回从头结点进入环的第一个节点。
运用题一,我们可以检查链表中是否有环。
如果有环,那么p1p2重合点p必然在环中。从p点断开环,
方法为:p1=p, p2=p->next, p->next=NULL。此时,原单链表可以看作两条单链表,
一条从head开始,另一条从p2开始,于是运用题二的方法,我们找到它们的第一个交点即为所求。
4.只给定单链表中某个结点p(并非最后一个结点,即p->next!=NULL)指针,删除该结点。
办法很简单,首先是放p中数据,然后将p->next的数据copy入p中,接下来删除p->next即可。
5.只给定单链表中某个结点p(非空结点),在p前面插入一个结点。
办法与前者类似,首先分配一个结点q,将q插入在p后,接下来将p中的数据copy入q中,
然后再将要插入的数据记录在p中。
78.链表和数组的区别在哪里?
分析:主要在基本概念上的理解。
但是最好能考虑的全面一点,现在公司招人的竞争可能就在细节上产生,
谁比较仔细,谁获胜的机会就大。
79.
1.编写实现链表排序的一种算法。说明为什么你会选择用这样的方法?
2.编写实现数组排序的一种算法。说明为什么你会选择用这样的方法?
3.请编写能直接实现strstr()函数功能的代码。
80.阿里巴巴一道笔试题
问题描述:
12个高矮不同的人,排成两排,每排必须是从矮到高排列,而且第二排比对应的第一排的人高,问排列方式有多少种?
这个笔试题,很YD,因为把某个递归关系隐藏得很深。
关于本微软等公司数据结构+算法面试100题系列的郑重声明
关于,本微软等公司数据结构+算法面试100题系列的郑重声明
-------------
作者:July
看此文之前,首先请区别于微软等100题系列(包含全部的题目+答案+资源)与100题原题目。
上个月,就这微软等100题系列,的版权在我俩篇博文中,已经有所说明,
=================
作者声明:
1.由于其中大部题目搜集于网络。有的流传甚广,个别题,我已无法考究,究竟最初源自哪里。
但,所有资料以如此形式,如此精选整理,的确是出自于我个人之手。
且题目的答案由我个人和一些网友完成。如此,我自称为作者,我想并不过分。
2.作者本人July对以上所有任何资料享有版权。转载请注明出处。谢谢。July。2010年10月27日。
=================================
在此,特意再郑重声明下:
一、本微软等公司数据结构+算法面试100题系列,所有任何全部的解释权归我个人所有。
二、本微软等100题系列,的全部题目的知识产权,归原公司微软、谷歌、腾讯、华为、百度等公司所有。
三、本微软等100题系列,的全部答案(特指已上传为资源共享)的版权,归我个人和我所发表的3个帖子上的部分网友所有。
四、本微软等100题系列,的资源下载的所有权,归我个人July所有。
五、凡是以July为名,不论是博客发表,帖子发表,还是资源上传,所有任何内容和资料,归July本人所有。
任何人,不得私自将此100题题目+答案,据为己有。凡是不注明作者July及出处者,必究。
六、本微软等100题系列,将永久更新,永久维护。不断更新此100题。
整理完了最初的100题V0.1版本后,会有不同的更新的另外100题V0.2、V0.3..版本。不断更新,去粗取精。
何谓版权?打个比喻就是,
中国汉字归全体中国人所有,但某一个人写或整理出了一篇文章,我们就说,这篇文章的版权归他个人所有。
微软公司等数据结构+算法面试100题(第1-100题)全部出炉
微软等公司数据结构+算法面试100题(第1-100题)首次完整亮相
作者:July、2010年12月6日。
-
更新:现今,这100题的答案已经全部整理出来了,微软面试100题2010年版全部答案集锦:http://blog.csdn.net/v_july_v/article/details/6870251。
-
以下100题中有部分题目整理自何海涛的博客(http://zhedahht.blog.163.com/)。十分感谢。
---------------------------------------------------
微软等100题系列V0.1版终于结束了。
从2010年10月11日当天最初发表前40题以来,直至此刻,整理这100题,已有近2个月。
2个月,因为要整理这100题,很多很多其它的事都被我强迫性的搁置一旁,
如今,要好好专心去做因这100题而被耽误的、其它的事了。
这微软等数据结构+算法面试100题系列(是的,系列),到底现在、或此刻、或未来,对初学者有多大的意义,
在此,我就不给予评说了。
由他们自己来认定。所谓,公道自在人心,我相信这句话。
任何人,对以下任何资料、题目、或答案,有任何问题,欢迎联系我。
作者邮箱:
作者声明:
转载或引用以下任何资料、或题目,请注明作者本人July及出处。
向您的厚道致敬,谢谢。
好了,请享受这完完整整的100题吧,这可是首次完整亮相哦。:D。
-----------------------------------
1.把二元查找树转变成排序的双向链表(树)
题目:
输入一棵二元查找树,将该二元查找树转换成一个排序的双向链表。
要求不能创建任何新的结点,只调整指针的指向。
10
/ /
6 14
/ / / /
4 8 12 16
转换成双向链表
4=6=8=10=12=14=16。
首先我们定义的二元查找树 节点的数据结构如下:
struct BSTreeNode
{
int m_nValue; // value of node
BSTreeNode *m_pLeft; // left child of node
BSTreeNode *m_pRight; // right child of node
};
2.设计包含min函数的栈(栈)
定义栈的数据结构,要求添加一个min函数,能够得到栈的最小元素。
要求函数min、push以及pop的时间复杂度都是O(1)。
3.求子数组的最大和(数组)
题目:
输入一个整形数组,数组里有正数也有负数。
数组中连续的一个或多个整数组成一个子数组,每个子数组都有一个和。
求所有子数组的和的最大值。要求时间复杂度为O(n)。
例如输入的数组为1, -2, 3, 10, -4, 7, 2, -5,和最大的子数组为3, 10, -4, 7, 2,
因此输出为该子数组的和18。
4.在二元树中找出和为某一值的所有路径(树)
题目:输入一个整数和一棵二元树。
从树的根结点开始往下访问一直到叶结点所经过的所有结点形成一条路径。
打印出和与输入整数相等的所有路径。
例如 输入整数22和如下二元树
10
/ /
5 12
/ /
4 7
则打印出两条路径:10, 12和10, 5, 7。
二元树节点的数据结构定义为:
struct BinaryTreeNode // a node in the binary tree
{
int m_nValue; // value of node
BinaryTreeNode *m_pLeft; // left child of node
BinaryTreeNode *m_pRight; // right child of node
};
5.查找最小的k个元素(数组)
题目:输入n个整数,输出其中最小的k个。
例如输入1,2,3,4,5,6,7和8这8个数字,则最小的4个数字为1,2,3和4。
第6题(数组)
腾讯面试题:
给你10分钟时间,根据上排给出十个数,在其下排填出对应的十个数
要求下排每个数都是先前上排那十个数在下排出现的次数。
上排的十个数如下:
【0,1,2,3,4,5,6,7,8,9】
举一个例子,
数值: 0,1,2,3,4,5,6,7,8,9
分配: 6,2,1,0,0,0,1,0,0,0
0在下排出现了6次,1在下排出现了2次,
2在下排出现了1次,3在下排出现了0次....
以此类推..
第7题(链表)
微软亚院之编程判断俩个链表是否相交
给出俩个单向链表的头指针,比如h1,h2,判断这俩个链表是否相交。
为了简化问题,我们假设俩个链表均不带环。
问题扩展:
1.如果链表可能有环列?
2.如果需要求出俩个链表相交的第一个节点列?
第8题(算法)
此贴选一些 比较怪的题,,由于其中题目本身与算法关系不大,仅考考思维。特此并作一题。
1.有两个房间,一间房里有三盏灯,另一间房有控制着三盏灯的三个开关,
这两个房间是 分割开的,从一间里不能看到另一间的情况。
现在要求受训者分别进这两房间一次,然后判断出这三盏灯分别是由哪个开关控制的。
有什么办法呢?
2.你让一些人为你工作了七天,你要用一根金条作为报酬。金条被分成七小块,每天给出一块。
如果你只能将金条切割两次,你怎样分给这些工人?
3. ★用一种算法来颠倒一个链接表的顺序。现在在不用递归式的情况下做一遍。
★用一种算法在一个循环的链接表里插入一个节点,但不得穿越链接表。
★用一种算法整理一个数组。你为什么选择这种方法?
★用一种算法使通用字符串相匹配。
★颠倒一个字符串。优化速度。优化空间。
★颠倒一个句子中的词的顺序,比如将“我叫克丽丝”转换为“克丽丝叫我”,
实现速度最快,移动最少。
★找到一个子字符串。优化速度。优化空间。
★比较两个字符串,用O(n)时间和恒量空间。
★假设你有一个用1001个整数组成的数组,这些整数是任意排列的,但是你知道所有的整数都在1到1000(包括1000)之间。此外,除一个数字出现两次外,其他所有数字只出现一次。假设你只能对这个数组做一次处理,用一种算法找出重复的那个数字。如果你在运算中使用了辅助的存储方式,那么你能找到不用这种方式的算法吗?
★不用乘法或加法增加8倍。现在用同样的方法增加7倍。
第9题(树)
判断整数序列是不是二元查找树的后序遍历结果
题目:输入一个整数数组,判断该数组是不是某二元查找树的后序遍历的结果。
如果是返回true,否则返回false。
例如输入5、7、6、9、11、10、8,由于这一整数序列是如下树的后序遍历结果:
8
/ /
6 10
/ / / /
5 7 9 11
因此返回true。
如果输入7、4、6、5,没有哪棵树的后序遍历的结果是这个序列,因此返回false。
第10题(字符串)
翻转句子中单词的顺序。
题目:输入一个英文句子,翻转句子中单词的顺序,但单词内字符的顺序不变。
句子中单词以空格符隔开。为简单起见,标点符号和普通字母一样处理。
例如输入“I am a student.”,则输出“student. a am I”。
第11题(树)
求二叉树中节点的最大距离...
如果我们把二叉树看成一个图,父子节点之间的连线看成是双向的,
我们姑且定义"距离"为两节点之间边的个数。
写一个程序,
求一棵二叉树中相距最远的两个节点之间的距离。
第12题(语法)
题目:求1+2+…+n,
要求不能使用乘除法、for、while、if、else、switch、case等关键字以及条件判断语句(A?B:C)。
第13题(链表):
题目:输入一个单向链表,输出该链表中倒数第k个结点。链表的倒数第0个结点为链表的尾指针。
链表结点定义如下:
struct ListNode
{
int m_nKey;
ListNode* m_pNext;
};
第14题(数组):
题目:输入一个已经按升序排序过的数组和一个数字,
在数组中查找两个数,使得它们的和正好是输入的那个数字。
要求时间复杂度是O(n)。如果有多对数字的和等于输入的数字,输出任意一对即可。
例如输入数组1、2、4、7、11、15和数字15。由于4+11=15,因此输出4和11。
第15题(树):
题目:输入一颗二元查找树,将该树转换为它的镜像,
即在转换后的二元查找树中,左子树的结点都大于右子树的结点。
用递归和循环两种方法完成树的镜像转换。
例如输入:
8
/ /
6 10
// //
5 7 9 11
输出:
8
/ /
10 6
// //
11 9 7 5
定义二元查找树的结点为:
struct BSTreeNode // a node in the binary search tree (BST)
{
int m_nValue; // value of node
BSTreeNode *m_pLeft; // left child of node
BSTreeNode *m_pRight; // right child of node
};
第16题(树):
题目(微软):
输入一颗二元树,从上往下按层打印树的每个结点,同一层中按照从左往右的顺序打印。
例如输入
8
/ /
6 10
/ / / /
5 7 9 11
输出8 6 10 5 7 9 11。
第17题(字符串):
题目:在一个字符串中找到第一个只出现一次的字符。如输入abaccdeff,则输出b。
分析:这道题是2006年google的一道笔试题。
第18题(数组):
题目:n个数字(0,1,…,n-1)形成一个圆圈,从数字0开始,
每次从这个圆圈中删除第m个数字(第一个为当前数字本身,第二个为当前数字的下一个数字)。
当一个数字删除后,从被删除数字的下一个继续删除第m个数字。
求出在这个圆圈中剩下的最后一个数字。
July:我想,这个题目,不少人已经 见识过了。
第19题(数组、递归):
题目:定义Fibonacci数列如下:
/ 0 n=0
f(n)= 1 n=1
/ f(n-1)+f(n-2) n=2
输入n,用最快的方法求该数列的第n项。
分析:在很多C语言教科书中讲到递归函数的时候,都会用Fibonacci作为例子。
因此很多程序员对这道题的递归解法非常熟悉,但....呵呵,你知道的。。
第20题(字符串):
题目:输入一个表示整数的字符串,把该字符串转换成整数并输出。
例如输入字符串"345",则输出整数345。
第21题(数组)
2010年中兴面试题
编程求解:
输入两个整数 n 和 m,从数列1,2,3.......n 中 随意取几个数,
使其和等于 m ,要求将其中所有的可能组合列出来.
第22题(推理):
有4张红色的牌和4张蓝色的牌,主持人先拿任意两张,再分别在A、B、C三人额头上贴任意两张牌,
A、B、C三人都可以看见其余两人额头上的牌,看完后让他们猜自己额头上是什么颜色的牌,
A说不知道,B说不知道,C说不知道,然后A说知道了。
请教如何推理,A是怎么知道的。
如果用程序,又怎么实现呢?
第23题(算法):
用最简单,最快速的方法计算出下面这个圆形是否和正方形相交。"
3D坐标系 原点(0.0,0.0,0.0)
圆形:
半径r = 3.0
圆心o = (*.*, 0.0, *.*)
正方形:
4个角坐标;
1:(*.*, 0.0, *.*)
2:(*.*, 0.0, *.*)
3:(*.*, 0.0, *.*)
4:(*.*, 0.0, *.*)
第24题(链表):
链表操作,单链表就地逆置,
第25题(字符串):
写一个函数,它的原形是int continumax(char *outputstr,char *intputstr)
功能:
在字符串中找出连续最长的数字串,并把这个串的长度返回,
并把这个最长数字串付给其中一个函数参数outputstr所指内存。
例如:"abcd12345ed125ss123456789"的首地址传给intputstr后,函数将返回9,
outputstr所指的值为123456789
26.左旋转字符串(字符串)
题目:
定义字符串的左旋转操作:把字符串前面的若干个字符移动到字符串的尾部。
如把字符串abcdef左旋转2位得到字符串cdefab。请实现字符串左旋转的函数。
要求时间对长度为n的字符串操作的复杂度为O(n),辅助内存为O(1)。
27.跳台阶问题(递归)
题目:一个台阶总共有n级,如果一次可以跳1级,也可以跳2级。
求总共有多少总跳法,并分析算法的时间复杂度。
这道题最近经常出现,包括MicroStrategy等比较重视算法的公司
都曾先后选用过个这道题作为面试题或者笔试题。
28.整数的二进制表示中1的个数(运算)
题目:输入一个整数,求该整数的二进制表达中有多少个1。
例如输入10,由于其二进制表示为1010,有两个1,因此输出2。
分析:
这是一道很基本的考查位运算的面试题。
包括微软在内的很多公司都曾采用过这道题。
29.栈的push、pop序列(栈)
题目:输入两个整数序列。其中一个序列表示栈的push顺序,
判断另一个序列有没有可能是对应的pop顺序。
为了简单起见,我们假设push序列的任意两个整数都是不相等的。
比如输入的push序列是1、2、3、4、5,那么4、5、3、2、1就有可能是一个pop系列。
因为可以有如下的push和pop序列:
push 1,push 2,push 3,push 4,pop,push 5,pop,pop,pop,pop,
这样得到的pop序列就是4、5、3、2、1。
但序列4、3、5、1、2就不可能是push序列1、2、3、4、5的pop序列。
30.在从1到n的正数中1出现的次数(数组)
题目:输入一个整数n,求从1到n这n个整数的十进制表示中1出现的次数。
例如输入12,从1到12这些整数中包含1 的数字有1,10,11和12,1一共出现了5次。
分析:这是一道广为流传的google面试题。
31.华为面试题(搜索):
一类似于蜂窝的结构的图,进行搜索最短路径(要求5分钟)
32.(数组、规划)
有两个序列a,b,大小都为n,序列元素的值任意整数,无序;
要求:通过交换a,b中的元素,使[序列a元素的和]与[序列b元素的和]之间的差最小。
例如:
var a=[100,99,98,1,2, 3];
var b=[1, 2, 3, 4,5,40];
33.(字符串)
实现一个挺高级的字符匹配算法:
给一串很长字符串,要求找到符合要求的字符串,例如目的串:123
1******3***2 ,12*****3这些都要找出来
其实就是类似一些和谐系统。。。。。
34.(队列)
实现一个队列。
队列的应用场景为:
一个生产者线程将int类型的数入列,一个消费者线程将int类型的数出列
35.(矩阵)
求一个矩阵中最大的二维矩阵(元素和最大).如:
1 2 0 3 4
2 3 4 5 1
1 1 5 3 0
中最大的是:
4 5
5 3
要求:(1)写出算法;(2)分析时间复杂度;(3)用C写出关键代码
第36题-40题(有些题目搜集于CSDN上的网友,已标明):
36.引用自网友:longzuo(运算)
谷歌笔试:
n支队伍比赛,分别编号为0,1,2。。。。n-1,已知它们之间的实力对比关系,
存储在一个二维数组w[n][n]中,w[i][j] 的值代表编号为i,j的队伍中更强的一支。
所以w[i][j]=i 或者j,现在给出它们的出场顺序,并存储在数组order[n]中,
比如order[n] = {4,3,5,8,1......},那么第一轮比赛就是 4对3, 5对8。.......
胜者晋级,败者淘汰,同一轮淘汰的所有队伍排名不再细分,即可以随便排,
下一轮由上一轮的胜者按照顺序,再依次两两比,比如可能是4对5,直至出现第一名
编程实现,给出二维数组w,一维数组order 和 用于输出比赛名次的数组result[n],
求出result。
37.(字符串)
有n个长为m+1的字符串,
如果某个字符串的最后m个字符与某个字符串的前m个字符匹配,则两个字符串可以联接,
问这n个字符串最多可以连成一个多长的字符串,如果出现循环,则返回错误。
38.(算法)
百度面试:
1.用天平(只能比较,不能称重)从一堆小球中找出其中唯一一个较轻的,使用x次天平,
最多可以从y个小球中找出较轻的那个,求y与x的关系式。
2.有一个很大很大的输入流,大到没有存储器可以将其存储下来,
而且只输入一次,如何从这个输入流中随机取得m个记录。
3.大量的URL字符串,如何从中去除重复的,优化时间空间复杂度
39.(树、图、算法)
网易有道笔试:
(1).
求一个二叉树中任意两个节点间的最大距离,
两个节点的距离的定义是 这两个节点间边的个数,
比如某个孩子节点和父节点间的距离是1,和相邻兄弟节点间的距离是2,优化时间空间复杂度。
(2).
求一个有向连通图的割点,割点的定义是,如果除去此节点和与其相关的边,
有向图不再连通,描述算法。
40.百度研发笔试题(栈、算法)
引用自:zp155334877
1)设计一个栈结构,满足一下条件:min,push,pop操作的时间复杂度为O(1)。
2)一串首尾相连的珠子(m个),有N种颜色(N<=10),
设计一个算法,取出其中一段,要求包含所有N中颜色,并使长度最短。
并分析时间复杂度与空间复杂度。
3)设计一个系统处理词语搭配问题,比如说 中国 和人民可以搭配,
则中国人民 人民中国都有效。要求:
*系统每秒的查询数量可能上千次;
*词语的数量级为10W;
*每个词至多可以与1W个词搭配
当用户输入中国人民的时候,要求返回与这个搭配词组相关的信息。
41.求固晶机的晶元查找程序(匹配、算法)
晶元盘由数目不详的大小一样的晶元组成,晶元并不一定全布满晶元盘,
照相机每次这能匹配一个晶元,如匹配过,则拾取该晶元,
若匹配不过,照相机则按测好的晶元间距移到下一个位置。
求遍历晶元盘的算法 求思路。
42.请修改append函数,利用这个函数实现(链表):
两个非降序链表的并集,1->2->3 和 2->3->5 并为 1->2->3->5
另外只能输出结果,不能修改两个链表的数据。
43.递归和非递归俩种方法实现二叉树的前序遍历。
44.腾讯面试题(算法):
1.设计一个魔方(六面)的程序。
2.有一千万条短信,有重复,以文本文件的形式保存,一行一条,有重复。
请用5分钟时间,找出重复出现最多的前10条。
3.收藏了1万条url,现在给你一条url,如何找出相似的url。(面试官不解释何为相似)
45.雅虎(运算、矩阵):
1.对于一个整数矩阵,存在一种运算,对矩阵中任意元素加一时,需要其相邻(上下左右)
某一个元素也加一,现给出一正数矩阵,判断其是否能够由一个全零矩阵经过上述运算得到。
2.一个整数数组,长度为n,将其分为m份,使各份的和相等,求m的最大值
比如{3,2,4,3,6} 可以分成{3,2,4,3,6} m=1;
{3,6}{2,4,3} m=2
{3,3}{2,4}{6} m=3 所以m的最大值为3
46.搜狐(运算):
四对括号可以有多少种匹配排列方式?比如两对括号可以有两种:()()和(())
47.创新工场(算法):
求一个数组的最长递减子序列 比如{9,4,3,2,5,4,3,2}的最长递减子序列为{9,5,4,3,2}
48.微软(运算):
一个数组是由一个递减数列左移若干位形成的,比如{4,3,2,1,6,5}
是由{6,5,4,3,2,1}左移两位形成的,在这种数组中查找某一个数。
49.一道看上去很吓人的算法面试题(排序、算法):
如何对n个数进行排序,要求时间复杂度O(n),空间复杂度O(1)
50.网易有道笔试(sorry,与第39题重复):
1.求一个二叉树中任意两个节点间的最大距离,两个节点的距离的定义是 这两个节点间边的个数,
比如某个孩子节点和父节点间的距离是1,和相邻兄弟节点间的距离是2,优化时间空间复杂度。
2.求一个有向连通图的割点,割点的定义是,
如果除去此节点和与其相关的边,有向图不再连通,描述算法。
-------------------------------------------------------------------
51.和为n连续正数序列(数组)。
题目:输入一个正数n,输出所有和为n连续正数序列。
例如输入15,由于1+2+3+4+5=4+5+6=7+8=15,所以输出3个连续序列1-5、4-6和7-8。
分析:这是网易的一道面试题。
52.二元树的深度(树)。
题目:输入一棵二元树的根结点,求该树的深度。
从根结点到叶结点依次经过的结点(含根、叶结点)形成树的一条路径,最长路径的长度为树的深度。
例如:输入二元树:
10
/ /
6 14
/ / /
4 12 16
输出该树的深度3。
二元树的结点定义如下:
struct SBinaryTreeNode // a node of the binary tree
{
int m_nValue; // value of node
SBinaryTreeNode *m_pLeft; // left child of node
SBinaryTreeNode *m_pRight; // right child of node
};
分析:这道题本质上还是考查二元树的遍历。
53.字符串的排列(字符串)。
题目:输入一个字符串,打印出该字符串中字符的所有排列。
例如输入字符串abc,则输出由字符a、b、c所能排列出来的所有字符串
abc、acb、bac、bca、cab和cba。
分析:这是一道很好的考查对递归理解的编程题,
因此在过去一年中频繁出现在各大公司的面试、笔试题中。
54.调整数组顺序使奇数位于偶数前面(数组)。
题目:输入一个整数数组,调整数组中数字的顺序,使得所有奇数位于数组的前半部分,
所有偶数位于数组的后半部分。要求时间复杂度为O(n)。
55.(语法)
题目:类CMyString的声明如下:
class CMyString
{
public:
CMyString(char* pData = NULL);
CMyString(const CMyString& str);
~CMyString(void);
CMyString& operator = (const CMyString& str);
private:
char* m_pData;
};
请实现其赋值运算符的重载函数,要求异常安全,即当对一个对象进行赋值时发生异常,对象的状态不能改变。
56.最长公共字串(算法、字符串)。
题目:如果字符串一的所有字符按其在字符串中的顺序出现在另外一个字符串二中,
则字符串一称之为字符串二的子串。
注意,并不要求子串(字符串一)的字符必须连续出现在字符串二中。
请编写一个函数,输入两个字符串,求它们的最长公共子串,并打印出最长公共子串。
例如:输入两个字符串BDCABA和ABCBDAB,字符串BCBA和BDAB都是是它们的最长公共子串,
则输出它们的长度4,并打印任意一个子串。
分析:求最长公共子串(Longest Common Subsequence, LCS)是一道非常经典的动态规划题,
因此一些重视算法的公司像MicroStrategy都把它当作面试题。
57.用俩个栈实现队列(栈、队列)。
题目:某队列的声明如下:
template<typename T> class CQueue
{
public:
CQueue() {}
~CQueue() {}
void appendTail(const T& node); // append a element to tail
void deleteHead(); // remove a element from head
private:
T> m_stack1;
T> m_stack2;
};
分析:从上面的类的声明中,我们发现在队列中有两个栈。
因此这道题实质上是要求我们用两个栈来实现一个队列。
相信大家对栈和队列的基本性质都非常了解了:栈是一种后入先出的数据容器,
因此对队列进行的插入和删除操作都是在栈顶上进行;队列是一种先入先出的数据容器,
我们总是把新元素插入到队列的尾部,而从队列的头部删除元素。
58.从尾到头输出链表(链表)。
题目:输入一个链表的头结点,从尾到头反过来输出每个结点的值。链表结点定义如下:
struct ListNode
{
int m_nKey;
ListNode* m_pNext;
};
分析:这是一道很有意思的面试题。
该题以及它的变体经常出现在各大公司的面试、笔试题中。
59.不能被继承的类(语法)。
题目:用C++设计一个不能被继承的类。
分析:这是Adobe公司2007年校园招聘的最新笔试题。
这道题除了考察应聘者的C++基本功底外,还能考察反应能力,是一道很好的题目。
60.在O(1)时间内删除链表结点(链表、算法)。
题目:给定链表的头指针和一个结点指针,在O(1)时间删除该结点。链表结点的定义如下:
struct ListNode
{
int m_nKey;
ListNode* m_pNext;
};
函数的声明如下:
void DeleteNode(ListNode* pListHead, ListNode* pToBeDeleted);
分析:这是一道广为流传的Google面试题,能有效考察我们的编程基本功,还能考察我们的反应速度,
更重要的是,还能考察我们对时间复杂度的理解。
-------------------------------------------------------------------------
61.找出数组中两个只出现一次的数字(数组)
题目:一个整型数组里除了两个数字之外,其他的数字都出现了两次。
请写程序找出这两个只出现一次的数字。要求时间复杂度是O(n),空间复杂度是O(1)。
分析:这是一道很新颖的关于位运算的面试题。
62.找出链表的第一个公共结点(链表)。
题目:两个单向链表,找出它们的第一个公共结点。
链表的结点定义为:
struct ListNode
{
int m_nKey;
ListNode* m_pNext;
};
分析:这是一道微软的面试题。微软非常喜欢与链表相关的题目,
因此在微软的面试题中,链表出现的概率相当高。
63.在字符串中删除特定的字符(字符串)。
题目:输入两个字符串,从第一字符串中删除第二个字符串中所有的字符。
例如,输入”They are students.”和”aeiou”,
则删除之后的第一个字符串变成”Thy r stdnts.”。
分析:这是一道微软面试题。在微软的常见面试题中,与字符串相关的题目占了很大的一部分,
因为写程序操作字符串能很好的反映我们的编程基本功。
64. 寻找丑数(运算)。
题目:我们把只包含因子2、3和5的数称作丑数(Ugly Number)。例如6、8都是丑数,
但14不是,因为它包含因子7。习惯上我们把1当做是第一个丑数。
求按从小到大的顺序的第1500个丑数。
分析:这是一道在网络上广为流传的面试题,据说google曾经采用过这道题。
65.输出1到最大的N位数(运算)
题目:输入数字n,按顺序输出从1最大的n位10进制数。比如输入3,
则输出1、2、3一直到最大的3位数即999。
分析:这是一道很有意思的题目。看起来很简单,其实里面却有不少的玄机。
66.颠倒栈(栈)。
题目:用递归颠倒一个栈。例如输入栈{1, 2, 3, 4, 5},1在栈顶。
颠倒之后的栈为{5, 4, 3, 2, 1},5处在栈顶。
67.俩个闲玩娱乐(运算)。
1.扑克牌的顺子
从扑克牌中随机抽5张牌,判断是不是一个顺子,即这5张牌是不是连续的。
2-10为数字本身,A为1,J为11,Q为12,K为13,而大小王可以看成任意数字。
2.n个骰子的点数。
把n个骰子扔在地上,所有骰子朝上一面的点数之和为S。输入n,
打印出S的所有可能的值出现的概率。
68.把数组排成最小的数(数组、算法)。
题目:输入一个正整数数组,将它们连接起来排成一个数,输出能排出的所有数字中最小的一个。
例如输入数组{32, 321},则输出这两个能排成的最小数字32132。
请给出解决问题的算法,并证明该算法。
分析:这是09年6月份百度的一道面试题,
从这道题我们可以看出百度对应聘者在算法方面有很高的要求。
69.旋转数组中的最小元素(数组、算法)。
题目:把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。输入一个排好序的数组的一个旋转,
输出旋转数组的最小元素。例如数组{3, 4, 5, 1, 2}为{1, 2, 3, 4, 5}的一个旋转,该数组的最小值为1。
分析:这道题最直观的解法并不难。从头到尾遍历数组一次,就能找出最小的元素,
时间复杂度显然是O(N)。但这个思路没有利用输入数组的特性,我们应该能找到更好的解法。
70.给出一个函数来输出一个字符串的所有排列(经典字符串问题)。
ANSWER 简单的回溯就可以实现了。当然排列的产生也有很多种算法,去看看组合数学,
还有逆序生成排列和一些不需要递归生成排列的方法。
印象中Knuth的<TAOCP>第一卷里面深入讲了排列的生成。这些算法的理解需要一定的数学功底,
也需要一定的灵感,有兴趣最好看看。
71.数值的整数次方(数字、运算)。
题目:实现函数double Power(double base, int exponent),求base的exponent次方。
不需要考虑溢出。
分析:这是一道看起来很简单的问题。可能有不少的人在看到题目后30秒写出如下的代码:
double Power(double base, int exponent)
{
double result = 1.0;
for(int i = 1; i <= exponent; ++i)
result *= base;
return result;
}
72.(语法)
题目:设计一个类,我们只能生成该类的一个实例。
分析:只能生成一个实例的类是实现了Singleton模式的类型。
73.对称字符串的最大长度(字符串)。
题目:输入一个字符串,输出该字符串中对称的子字符串的最大长度。
比如输入字符串“google”,由于该字符串里最长的对称子字符串是“goog”,因此输出4。
分析:可能很多人都写过判断一个字符串是不是对称的函数,这个题目可以看成是该函数的加强版。
74.数组中超过出现次数超过一半的数字(数组)
题目:数组中有一个数字出现的次数超过了数组长度的一半,找出这个数字。
分析:这是一道广为流传的面试题,包括百度、微软和Google在内的多家公司都
曾经采用过这个题目。要几十分钟的时间里很好地解答这道题,
除了较好的编程能力之外,还需要较快的反应和较强的逻辑思维能力。
75.二叉树两个结点的最低共同父结点(树)
题目:二叉树的结点定义如下:
struct TreeNode
{
int m_nvalue;
TreeNode* m_pLeft;
TreeNode* m_pRight;
};
输入二叉树中的两个结点,输出这两个结点在数中最低的共同父结点。
分析:求数中两个结点的最低共同结点是面试中经常出现的一个问题。这个问题至少有两个变种。
76.复杂链表的复制(链表、算法)
题目:有一个复杂链表,其结点除了有一个m_pNext指针指向下一个结点外,
还有一个m_pSibling指向链表中的任一结点或者NULL。其结点的C++定义如下:
struct ComplexNode
{
int m_nValue;
ComplexNode* m_pNext;
ComplexNode* m_pSibling;
};
下图是一个含有5个结点的该类型复杂链表。
图中实线箭头表示m_pNext指针,虚线箭头表示m_pSibling指针。为简单起见,
指向NULL的指针没有画出。
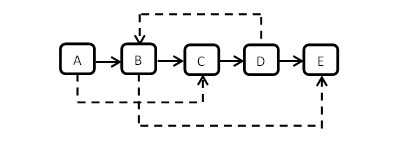
请完成函数ComplexNode* Clone(ComplexNode* pHead),以复制一个复杂链表。
分析:在常见的数据结构上稍加变化,这是一种很新颖的面试题。
要在不到一个小时的时间里解决这种类型的题目,我们需要较快的反应能力,
对数据结构透彻的理解以及扎实的编程功底。
77.关于链表问题的面试题目如下(链表):
1.给定单链表,检测是否有环。
使用两个指针p1,p2从链表头开始遍历,p1每次前进一步,p2每次前进两步。如果p2到达链表尾部,
说明无环,否则p1、p2必然会在某个时刻相遇(p1==p2),从而检测到链表中有环。
2.给定两个单链表(head1, head2),检测两个链表是否有交点,如果有返回第一个交点。
如果head1==head2,那么显然相交,直接返回head1。
否则,分别从head1,head2开始遍历两个链表获得其长度len1与len2,假设len1>=len2,
那么指针p1由head1开始向后移动len1-len2步,指针p2=head2,
下面p1、p2每次向后前进一步并比较p1p2是否相等,如果相等即返回该结点,
否则说明两个链表没有交点。
3.给定单链表(head),如果有环的话请返回从头结点进入环的第一个节点。
运用题一,我们可以检查链表中是否有环。
如果有环,那么p1p2重合点p必然在环中。从p点断开环,
方法为:p1=p, p2=p->next, p->next=NULL。此时,原单链表可以看作两条单链表,
一条从head开始,另一条从p2开始,于是运用题二的方法,我们找到它们的第一个交点即为所求。
4.只给定单链表中某个结点p(并非最后一个结点,即p->next!=NULL)指针,删除该结点。
办法很简单,首先是放p中数据,然后将p->next的数据copy入p中,接下来删除p->next即可。
5.只给定单链表中某个结点p(非空结点),在p前面插入一个结点。
办法与前者类似,首先分配一个结点q,将q插入在p后,接下来将p中的数据copy入q中,
然后再将要插入的数据记录在p中。
78.链表和数组的区别在哪里(链表、数组)?
分析:主要在基本概念上的理解。
但是最好能考虑的全面一点,现在公司招人的竞争可能就在细节上产生,
谁比较仔细,谁获胜的机会就大。
79.(链表、字符串)
1.编写实现链表排序的一种算法。说明为什么你会选择用这样的方法?
2.编写实现数组排序的一种算法。说明为什么你会选择用这样的方法?
3.请编写能直接实现strstr()函数功能的代码。
80.阿里巴巴一道笔试题(运算、算法)
问题描述:
12个高矮不同的人,排成两排,每排必须是从矮到高排列,而且第二排比对应的第一排的人高,问排列方式有多少种?
这个笔试题,很YD,因为把某个递归关系隐藏得很深。
先来几组百度的面试题:
===================
81.第1组百度面试题
1.一个int数组,里面数据无任何限制,要求求出所有这样的数a[i],
其左边的数都小于等于它,右边的数都大于等于它。
能否只用一个额外数组和少量其它空间实现。
2.一个文件,内含一千万行字符串,每个字符串在1K以内,
要求找出所有相反的串对,如abc和cba。
3.STL的set用什么实现的?为什么不用hash?
82.第2组百度面试题
1.给出两个集合A和B,其中集合A={name},
集合B={age、sex、scholarship、address、...},
要求:
问题1、根据集合A中的name查询出集合B中对应的属性信息;
问题2、根据集合B中的属性信息(单个属性,如age<20等),查询出集合A中对应的name。
2.给出一个文件,里面包含两个字段{url、size},
即url为网址,size为对应网址访问的次数,
要求:
问题1、利用Linux Shell命令或自己设计算法,
查询出url字符串中包含“baidu”子字符串对应的size字段值;
问题2、根据问题1的查询结果,对其按照size由大到小的排列。
(说明:url数据量很大,100亿级以上)
83.第3组百度面试题
1.今年百度的一道题目
百度笔试:给定一个存放整数的数组,重新排列数组使得数组左边为奇数,右边为偶数。
要求:空间复杂度O(1),时间复杂度为O(n)。
2.百度笔试题
用C语言实现函数void * memmove(void *dest, const void *src, size_t n)。
memmove函数的功能是拷贝src所指的内存内容前n个字节到dest所指的地址上。
分析:
由于可以把任何类型的指针赋给void类型的指针
这个函数主要是实现各种数据类型的拷贝。
84.第4组百度面试题
2010年3道百度面试题[相信,你懂其中的含金量]
1.a~z包括大小写与0~9组成的N个数
用最快的方式把其中重复的元素挑出来。
2.已知一随机发生器,产生0的概率是p,产生1的概率是1-p,现在要你构造一个发生器,
使得它构造0和1的概率均为1/2;构造一个发生器,使得它构造1、2、3的概率均为1/3;...,
构造一个发生器,使得它构造1、2、3、...n的概率均为1/n,要求复杂度最低。
3.有10个文件,每个文件1G,
每个文件的每一行都存放的是用户的query,每个文件的query都可能重复。
要求按照query的频度排序.
85.又见字符串的问题
1.给出一个函数来复制两个字符串A和B。
字符串A的后几个字节和字符串B的前几个字节重叠。
分析:记住,这种题目往往就是考你对边界的考虑情况。
2.已知一个字符串,比如asderwsde,寻找其中的一个子字符串比如sde的个数,
如果没有返回0,有的话返回子字符串的个数。
86.
怎样编写一个程序,把一个有序整数数组放到二叉树中?
分析:本题考察二叉搜索树的建树方法,简单的递归结构。
关于树的算法设计一定要联想到递归,因为树本身就是递归的定义。
而,学会把递归改称非递归也是一种必要的技术。
毕竟,递归会造成栈溢出,关于系统底层的程序中不到非不得以最好不要用。
但是对某些数学问题,就一定要学会用递归去解决。
87.
1.大整数数相乘的问题。(这是2002年在一考研班上遇到的算法题)
2.求最大连续递增数字串(如“ads3sl456789DF3456ld345AA”中的“456789”)
3.实现strstr功能,即在父串中寻找子串首次出现的位置。
(笔试中常让面试者实现标准库中的一些函数)
88.2005年11月金山笔试题。编码完成下面的处理函数。
函数将字符串中的字符'*'移到串的前部分,
前面的非'*'字符后移,但不能改变非'*'字符的先后顺序,函数返回串中字符'*'的数量。
如原始串为:ab**cd**e*12,
处理后为*****abcde12,函数并返回值为5。(要求使用尽量少的时间和辅助空间)
89.神州数码、华为、东软笔试题
1.2005年11月15日华为软件研发笔试题。实现一单链表的逆转。
2.编码实现字符串转整型的函数(实现函数atoi的功能),据说是神州数码笔试题。如将字符
串 ”+123”123, ”-0123”-123, “123CS45”123, “123.45CS”123, “CS123.45”0
3.快速排序(东软喜欢考类似的算法填空题,又如堆排序的算法等)
4.删除字符串中的数字并压缩字符串。
如字符串”abc123de4fg56”处理后变为”abcdefg”。注意空间和效率。
(下面的算法只需要一次遍历,不需要开辟新空间,时间复杂度为O(N))
5.求两个串中的第一个最长子串(神州数码以前试题)。
如"abractyeyt","dgdsaeactyey"的最大子串为"actyet"。
90.
1.不开辟用于交换数据的临时空间,如何完成字符串的逆序
(在技术一轮面试中,有些面试官会这样问)。
2.删除串中指定的字符
(做此题时,千万不要开辟新空间,否则面试官可能认为你不适合做嵌入式开发)
3.判断单链表中是否存在环。
91.
1.一道著名的毒酒问题
有1000桶酒,其中1桶有毒。而一旦吃了,毒性会在1周后发作。
现在我们用小老鼠做实验,要在1周内找出那桶毒酒,问最少需要多少老鼠。
2.有趣的石头问题
有一堆1万个石头和1万个木头,对于每个石头都有1个木头和它重量一样,
把配对的石头和木头找出来。
92.
1.多人排成一个队列,我们认为从低到高是正确的序列,但是总有部分人不遵守秩序。
如果说,前面的人比后面的人高(两人身高一样认为是合适的),
那么我们就认为这两个人是一对“捣乱分子”,比如说,现在存在一个序列:
176, 178, 180, 170, 171
这些捣乱分子对为
<176, 170>, <176, 171>, <178, 170>, <178, 171>, <180, 170>, <180, 171>,
那么,现在给出一个整型序列,请找出这些捣乱分子对的个数(仅给出捣乱分子对的数目即可,不用具体的对)
要求:
输入:
为一个文件(in),文件的每一行为一个序列。序列全为数字,数字间用”,”分隔。
输出:
为一个文件(out),每行为一个数字,表示捣乱分子的对数。
详细说明自己的解题思路,说明自己实现的一些关键点。
并给出实现的代码 ,并分析时间复杂度。
限制:
输入每行的最大数字个数为100000个,数字最长为6位。程序无内存使用限制。
93.在一个int数组里查找这样的数,它大于等于左侧所有数,小于等于右侧所有数。
直观想法是用两个数组a、b。a[i]、b[i]分别保存从前到i的最大的数和从后到i的最小的数,
一个解答:这需要两次遍历,然后再遍历一次原数组,
将所有data[i]>=a[i-1]&&data[i]<=b[i]的data[i]找出即可。
给出这个解答后,面试官有要求只能用一个辅助数组,且要求少遍历一次。
94.微软笔试题
求随机数构成的数组中找到长度大于=3的最长的等差数列9 d- x' W) w9 ?" o3 b0 R
输出等差数列由小到大:
如果没有符合条件的就输出
格式:
输入[1,3,0,5,-1,6]
输出[-1,1,3,5]
要求时间复杂度,空间复杂度尽量小
95.华为面试题
1 判断一字符串是不是对称的,如:abccba
2.用递归的方法判断整数组a[N]是不是升序排列
96.08年中兴校园招聘笔试题
1.编写strcpy 函数
已知strcpy 函数的原型是
char *strcpy(char *strDest, const char *strSrc);
其中strDest 是目的字符串,strSrc 是源字符串。不调用C++/C 的字符串库函数,请
编写函数 strcpy
最后压轴之戏,终结此微软等100题系列V0.1版。
那就,
连续来几组微软公司的面试题,让你一次爽个够:
======================
97.第1组微软较简单的算法面试题
1.编写反转字符串的程序,要求优化速度、优化空间。
2.在链表里如何发现循环链接?
3.编写反转字符串的程序,要求优化速度、优化空间。
4.给出洗牌的一个算法,并将洗好的牌存储在一个整形数组里。
5.写一个函数,检查字符是否是整数,如果是,返回其整数值。
(或者:怎样只用4行代码编写出一个从字符串到长整形的函数?)
98.第2组微软面试题
1.给出一个函数来输出一个字符串的所有排列。
2.请编写实现malloc()内存分配函数功能一样的代码。
3.给出一个函数来复制两个字符串A和B。字符串A的后几个字节和字符串B的前几个字节重叠。
4.怎样编写一个程序,把一个有序整数数组放到二叉树中?
5.怎样从顶部开始逐层打印二叉树结点数据?请编程。
6.怎样把一个链表掉个顺序(也就是反序,注意链表的边界条件并考虑空链表)?
99.第3组微软面试题
1.烧一根不均匀的绳,从头烧到尾总共需要1个小时。
现在有若干条材质相同的绳子,问如何用烧绳的方法来计时一个小时十五分钟呢?
2.你有一桶果冻,其中有黄色、绿色、红色三种,闭上眼睛抓取同种颜色的两个。
抓取多少个就可以确定你肯定有两个同一颜色的果冻?(5秒-1分钟)
3.如果你有无穷多的水,一个3公升的提捅,一个5公升的提捅,两只提捅形状上下都不均匀,
问你如何才能准确称出4公升的水?(40秒-3分钟)
一个岔路口分别通向诚实国和说谎国。
来了两个人,已知一个是诚实国的,另一个是说谎国的。
诚实国永远说实话,说谎国永远说谎话。现在你要去说谎国,
但不知道应该走哪条路,需要问这两个人。请问应该怎么问?(20秒-2分钟)
100.第4组微软面试题,挑战思维极限
1.12个球一个天平,现知道只有一个和其它的重量不同,问怎样称才能用三次就找到那个球。
13个呢?(注意此题并未说明那个球的重量是轻是重,所以需要仔细考虑)(5分钟-1小时)
2.在9个点上画10条直线,要求每条直线上至少有三个点?(3分钟-20分钟)
3.在一天的24小时之中,时钟的时针、分针和秒针完全重合在一起的时候有几次?
都分别是什么时间?你怎样算出来的?(5分钟-15分钟)
终结附加题:
微软面试题,挑战你的智商
==========
说明:如果你是第一次看到这种题,并且以前从来没有见过类似的题型,
并且能够在半个小时之内做出答案,说明你的智力超常..)
1.第一题 . 五个海盗抢到了100颗宝石,每一颗都一样大小和价值连城。他们决定这么分:
抽签决定自己的号码(1、2、3、4、5)
首先,由1号提出分配方案,然后大家表决,当且仅当超过半数的人同意时,
按照他的方案进行分配,否则将被扔进大海喂鲨鱼
如果1号死后,再由2号提出分配方案,然后剩下的4人进行表决,
当且仅当超过半数的人同意时,按照他的方案进行分配,否则将被扔入大海喂鲨鱼。
依此类推
条件:每个海盗都是很聪明的人,都能很理智地做出判断,从而做出选择。
问题:第一个海盗提出怎样的分配方案才能使自己的收益最大化?
2.一道关于飞机加油的问题,已知:
每个飞机只有一个油箱,
飞机之间可以相互加油(注意是相互,没有加油机)
一箱油可供一架飞机绕地球飞半圈,
问题:
为使至少一架飞机绕地球一圈回到起飞时的飞机场,至少需要出动几架飞机?
(所有飞机从同一机场起飞,而且必须安全返回机场,不允许中途降落,中间没有飞机场)
//欢迎,关注另外不同的更精彩的100题V0.2版,和此V0.1版的答案等后续内容。
完。
微软等100题系列V0.1版:c/c++基础面试题集锦
微软等100题系列V1.0版整理I:c/c++基础面试题集锦
July 2010年12月14日
-----------------------------------------
应网友要求和建议,特此把微软等公司数据结构+算法面试100题系列V0.1版,分门别类、彻底整理下。
一来为了让各位朋友看着清晰明了,二来为了让大家对这100题有个总体印象。
即微软等各大公司对数据结构+算法的考察,最喜欢考察那些结构,那些算法,着重点、重点考察在哪些方面。
所以,我现在把这些个着重点、重点给提炼出来,为了更方便的给大家分享。
我把这微软等100题系列V0.1版,分了以下几个方面:
1.c/c++基础
2.链表
3.栈堆队列
4.字符串 + 数组
5.树 + 图
6.数字游戏
7.思维推理 算法
8.百度、腾讯、微软三公司题目集锦。
每一分类,即一篇文章,此整理系列,即是八篇文章。
谢谢各位。:D。
好的,咱们,开始吧,请看:
=============
第一章 c/c++基础面试
55.
题目:类CMyString的声明如下:
class CMyString
{
public:
CMyString(char* pData = NULL);
CMyString(const CMyString& str);
~CMyString(void);
CMyString& operator = (const CMyString& str);
private:
char* m_pData;
};
请实现其赋值运算符的重载函数,要求异常安全,
即当对一个对象进行赋值时发生异常,对象的状态不能改变。
59.不能被继承的类。
题目:用C++设计一个不能被继承的类。
分析:这是Adobe公司2007年校园招聘的最新笔试题。
这道题除了考察应聘者的C++基本功底外,还能考察反应能力,是一道很好的题目。
72.
题目:设计一个类,我们只能生成该类的一个实例。
分析:只能生成一个实例的类是实现了Singleton模式的类型。
//此类c/c++基础面试题,完。
欢迎,你对以上任何一题,发表你的见解、看法、和思路。
谢谢。
微软等100题系列V0.1版:链表面试题集锦
微软等100题系列V0.1版整理II:链表面试题集锦
--
July 2010年12月14日
=======================
此微软等100题系列V0.1版,关于链表的面试题,占了11道。
链表,在数据结构中,也是一个最基本的重头戏。
请看:
--------------
第7题
微软亚院之编程判断俩个链表是否相交
给出俩个单向链表的头指针,比如h1,h2,判断这俩个链表是否相交。
为了简化问题,我们假设俩个链表均不带环。
问题扩展:
1.如果链表可能有环列?
2.如果需要求出俩个链表相交的第一个节点列?
第13题:
题目:输入一个单向链表,输出该链表中倒数第k个结点。
链表的倒数第0个结点为链表的尾指针。
链表结点定义如下:
struct ListNode
{
int m_nKey;
ListNode* m_pNext;
};
第24题:
链表操作,
(1).单链表就地逆置,
(2)合并链表
42.请修改append函数,利用这个函数实现:
两个非降序链表的并集,1->2->3 和 2->3->5 并为 1->2->3->5
另外只能输出结果,不能修改两个链表的数据。
58.从尾到头输出链表。
题目:输入一个链表的头结点,从尾到头反过来输出每个结点的值。
链表结点定义如下:
struct ListNode
{
int m_nKey;
ListNode* m_pNext;
};
分析:这是一道很有意思的面试题。
该题以及它的变体经常出现在各大公司的面试、笔试题中。
60.在O(1)时间内删除链表结点。
题目:给定链表的头指针和一个结点指针,在O(1)时间删除该结点。
链表结点的定义如下:
struct ListNode
{
int m_nKey;
ListNode* m_pNext;
};
函数的声明如下:
void DeleteNode(ListNode* pListHead, ListNode* pToBeDeleted);
分析:这是一道广为流传的Google面试题,能有效考察我们的编程基本功,
还能考察我们的反应速度,更重要的是,还能考察我们对时间复杂度的理解。
62.找出链表的第一个公共结点。
题目:两个单向链表,找出它们的第一个公共结点。
链表的结点定义为:
struct ListNode
{
int m_nKey;
ListNode* m_pNext;
};
分析:这是一道微软的面试题。微软非常喜欢与链表相关的题目,
因此在微软的面试题中,链表出现的概率相当高。
76.复杂链表的复制
题目:有一个复杂链表,其结点除了有一个m_pNext指针指向下一个结点外,
还有一个m_pSibling指向链表中的任一结点或者NULL。其结点的C++定义如下:
struct ComplexNode
{
int m_nValue;
ComplexNode* m_pNext;
ComplexNode* m_pSibling;
};
下图是一个含有5个结点的该类型复杂链表。
图中实线箭头表示m_pNext指针,虚线箭头表示m_pSibling指针。为简单起见,
指向NULL的指针没有画出。
请完成函数ComplexNode* Clone(ComplexNode* pHead),以复制一个复杂链表。
分析:在常见的数据结构上稍加变化,这是一种很新颖的面试题。
要在不到一个小时的时间里解决这种类型的题目,我们需要较快的反应能力,
对数据结构透彻的理解以及扎实的编程功底。
77.关于链表问题的面试题目如下:
1.给定单链表,检测是否有环。
使用两个指针p1,p2从链表头开始遍历,p1每次前进一步,p2每次前进两步。
如果p2到达链表尾部,说明无环,
否则p1、p2必然会在某个时刻相遇(p1==p2),从而检测到链表中有环。
2.给定两个单链表(head1, head2),检测两个链表是否有交点,如果有返回第一个交点。
如果head1==head2,那么显然相交,直接返回head1。
否则,分别从head1,head2开始遍历两个链表获得其长度len1与len2,假设len1>=len2,
那么指针p1由head1开始向后移动len1-len2步,指针p2=head2,
下面p1、p2每次向后前进一步并比较p1p2是否相等,如果相等即返回该结点,
否则说明两个链表没有交点。
3.给定单链表(head),如果有环的话请返回从头结点进入环的第一个节点。
运用题一,我们可以检查链表中是否有环。
如果有环,那么p1p2重合点p必然在环中。从p点断开环,
方法为:p1=p, p2=p->next, p->next=NULL。
此时,原单链表可以看作两条单链表,一条从head开始,另一条从p2开始,
于是运用题二的方法,我们找到它们的第一个交点即为所求。
4.只给定单链表中某个结点p(并非最后一个结点,即p->next!=NULL)指针,删除该结点。
办法很简单,首先是放p中数据,然后将p->next的数据copy入p中,接下来删除p->next即可。
5.只给定单链表中某个结点p(非空结点),在p前面插入一个结点。
办法与前者类似,首先分配一个结点q,将q插入在p后,接下来将p中的数据copy入q中,
然后再将要插入的数据记录在p中。
78.链表和数组的区别在哪里?
分析:主要在基本概念上的理解。
但是最好能考虑的全面一点,现在公司招人的竞争可能就在细节上产生,
谁比较仔细,谁获胜的机会就大。
79.
1.编写实现链表排序的一种算法。说明为什么你会选择用这样的方法?
2.编写实现数组排序的一种算法。说明为什么你会选择用这样的方法?
3.请编写能直接实现strstr()函数功能的代码。
//此链表面试题类,完。
欢迎,你对以上任何一题,提出你见解、思路、算法。
谢谢。:D。
微软等面试100题系列之网友精彩回复 [一]
微软等数据结构+算法面试100题系列之网友精彩回复 [一]
------------------------------
作者:July 飞雪
一直不断有网友来信,想要微软等100题的答案,可由于整理这100题的答案,分量太大。
所以,后60题的答案,一直迟迟未得出炉。我也早已经在前面的博文中,有所阐述:
=====
由于答案的整理不像题目那般,除了自己所有的,还可以从网上搜集,
而这个答案,全都得由自己去想、去做,更是由于这些题现已经有近10万人看到或见识到。
如此,更兼诚惶诚恐,不敢大肆造次。
我也将,更加细致的整理本100题V0.1版最后60题第41题-100题的答案,
所以希望,各位更加耐心的等待。
=======================
但,网友热切盼望的心情,实不敢有丁点辜负。
正好,有一群不错的,极具热心的网友,
在我发表的帖子上,一直在孜孜不倦的思考,不畏100题分量之大,一点一点的做这100题。
正好可以整理,贴出来作为各位后来网友的思路参考,于是,本文,就产生了。
首先,向所有在我帖子上,回复了自己独立而完整的思路的,所有热心的网友,表示衷心的感谢与致敬。
为了表示对他们劳动成果的尊重,接下来,除了继续分类整理这100题的同时,
我将把一些网友的精彩回复,整理到我的博客里。
同时,希望各位能对以下任何网友给出的思路,毫不犹豫的给出批评、指正。
并特别的期待,你也能贡献你的思路、或者更好的想法、算法。
谢谢。
----------------------
完整100题,请参见,
[珍藏版]微软等数据结构+算法面试100题全部出炉[100题首次完整亮相]
http://blog.csdn.net/v_JULY_v/archive/2010/12/06/6057286.aspx
以下所有的思路、答案选自网友飞雪在我这帖子上的回复:
本微软等100题系列V0.1版,永久维护(网友,思路回复)地址:
http://topic.csdn.net/u/20101126/10/b4f12a00-6280-492f-b785-cb6835a63dc9.html
//当然,继续欢迎,各位把自己针对此100题中任何一道,给出自己的思路,回复于上述帖子上。:D。
-----------------------------------------------------------------
为了表示对飞雪最大的尊重,我没有对他的回复做任何修改与改动。
欢迎,各位,毫不犹豫的,对他的思路、或解法提出质疑、批评、指正。谢谢。
飞雪:
第一题,改为循环链表做。
左边返回循环链表的最后一个元素,右边也返回,于是就可以返回加上根的循环链表了。
最后把循环部分断开,为所求。
第二题,似乎是今年很热的题,略。
第三题,最大子段和,略。
几个类似问题:
1.问这样的子串有多少个。
2.如果是首尾相连的,那么最大子串和是多少,有多少个。
3.如果是首尾相连的,取两个不相交子串,那么最大子串和是多少。
第四题,dfs。
第五题,一般可以用类似二分的,丢弃一半,这是渐近线性的算法。
还可以分为若干个桶,然后可以知道第k个在哪个桶里,这种算法比较稳定,如果输入比较均匀,表现可能较好。
另外,如果输入是有一定分布规律的话,可以取其中一部分进行采样,然后得到一个估计,然后再在这个估计的基础上优化。
第6题
直觉是有很多元素是0,所以可以先确定0的,然后再凭感觉做后面的。
第7题
似乎很古老了,略。
一个新问题:
结点里多了一个指针Node* x;指向链表中另一个元素,要求复制一个相同的链表。
第8题
...
第9题
预处题可以在nlogn内查询子段最大,最小值。
枚举根,查询左边和右边最小和最大值,于是可以知道根是不是合法的,如果合法,然后可以转换为子问题是不是合法。
另外似乎也可以不用做RMQ的预处理,因为枚举根是O(n)的,而求区间最大最小值也是O(n)的,RMQ会多一点东西出来。
复杂度大概是O(n^2)吧。
第10题
略
第9题补充,
总共O(n^2)个状态,O(n)的转移,所以复杂度上限是O(n^3),但是实际上可能只有O(n^2)。
第11题
用dp[i]表示结点i上子问题的解,h[i]表示i子树的高度。
于是i的解可能是:i的高度,两个最高的子树的高度和加1(如果子树大于等于2),子问题上的解。
第12题
暂时没想法,本来想用位移计算n^2但是要判断某一位是不是1。
第13题
构造两个步长差为k的指针,然后同时移动。
主要是优化常数了。
第14题
for (int i = 0, j = n - 1; i < j;)
{
int t = data[i] + data[j];
if (t == value) ok;
if (t > value) --j;
else ++i;
}
第15题
递归的直接应用,如果要求循环,估计也是伪的,是直接把递归化为循环那种。
至于直接用循环的,还没想法。
第16题
利用队列做层次遍历,似乎也很老了。
第17题
貌似开个ascii上限的数组遍历就行了。
第18题
很老的题了。
给几个变种吧:
要求输出第一个的,而报数是在按a1, a2, a3, ..., ax的顺序报,也就是说第一次报a1的出局,第二次报到a2的出局,报到ax后又重新来。似乎是09年某个regional的题。
要求输出最后一个的,n大概是10亿,k是不超过1000,在hdoj上有。
还有就是2n个人,前面的是坏人,后面的是好人,要求好后在坏人后出去,求最小的k,也是old题了。
第19题
如果精度要求不高,直接解差分方程。
如果精度要求高,可以用大数加矩阵二分。
第20题
似乎没啥难度。
第21题
npc难问题。
这里只给出n不大,用位俺码来表示集合,枚举所有含m个元素的集合的算法:
int x = comb & -comb, y = comb + x;
comb = ((comb & ~y) / x >> 1) | y;
来源是topcoder.
第22题
逻辑推理吧,如果用程序的话,可能就是枚举所有情况,然后一步一步判断,注意前后关系。
第23题
在x-z平面上做。
第24题
似乎又是老的了。
第25题
用一个自动机扫描过去就OK了。
开始状态,字符状态,数字状态,结束状态。
26.左旋转字符串
两种做法:
1.分别就地翻转后再整体翻转,但是隐藏的常数偏大。
2.转换分解为循环,可能内存会大一点点,还有就是__gcd算法,但是最小复制的。
27.跳台阶问题
免子数,前面有提。
28.整数的二进制表示中1的个数
可以用x&(x-1)技巧,可以分段打表,也可以用内建函数__builtin_popcount,还可以位加法并对其优化。
29.栈的push、pop序列
问题可以加强为,push的元素是从小到大的,也可以知道这两个问题是等价的,但是转换过程是nlogn。
既然push是从小到大的,于是问题就灰常好解决了。
30.在从1到n的正数中1出现的次数
按位dp,计算每一位中出现的次数。
31.华为面试题:
无图无真相
32.
问题等价于给定n+m个元素,分为两部分,其中一部分为n个元素。
用dp[i][j]表示从这n+m个元素中先i个出来是不是能组成一个j。
于是i最大为min(n, m),再遍历一次可以求解。
空间复杂度可以优化到O(全部的和)。
但是这样的话,要求所有的和不太大。
33.
似乎没有读懂,例子貌似只要统计1,2,3的次数就行了。
34.
似乎是OS上经典的问题了。
35.
枚举行O(N^2)
在列上做最大子段和O(M)。
36.引用自网友:longzuo
谷歌笔试
没仔细读。
37.
可能题目有小bug,最好假定串互不包含,否则会有些比较fuckable的情况。
然后就是预处理建拓扑图,求个最长路出来了。
38.
(3^n-1)/2
这个题目至少是2006年以前的了,做过。
39
39.1老题
39.2简单的dfs
40
似乎也很老了,不再回答了。
41.求固晶机的晶元查找程序
表示没读懂。
42.请修改append函数,利用这个函数实现:
似乎就是归并过程,取需要的部分。
43.递归和非递归俩种方法实现二叉树的前序遍历。
……加强为不准用辅助栈。
44.腾讯面试题:
……
45.雅虎:
45.1
每个点有个坐标(i,j)根据i+j的奇偶性,于是数字可以分为两组。
于是,这两组的和要相等。
45.2
似乎可以枚举m再做搜索。
46.搜狐:
catalan数
47.创新工场:
经典的dp了。
48.微软:
似乎还是直接二分。
如果序列从中间断为两部分,至多有一部分是一个递减序列循环移动而成的,并且是可判断的。
递归时,判断两部分的性质,对于递减的,可以知道是不是在里面,对于不满足递减性质的,可以递归地处理。
49.一道看上去很吓人的算法面试题:
神题,表示没想法。
50.网易有道笔试:
似乎重复了。
51.和为n连续正数序列
这个似乎不是网易的,而是05年百度之星的。
枚举划分的个数就行了,注意一下枚举的范围。
52.二元树的深度。
dfs
53.字符串的排列。
略
54.调整数组顺序使奇数位于偶数前面。
参考归并排序的inplace merge.
55.
题目:类CMyString的声明如下:
略
补充一下51:
如果划分为奇数个,那么n能被中间那个数整除,且n/划分个数就是中间那个数。
如果划分为偶数个,中间两个数的和和整除n的,刚好是n/(划分个数的一半)。
补充一下54:
好像直接inplace merge是不对的
可以用两个指针分别指向操作后的两个开始位置,然后扫描。
都扫描到不合法的为止,然后交换。然后继续扫描。。。
修改33楼,“NPC难问题”没这个说法,多打了一个C字,应该是“NP-难问题”,这和NP完全问题是不同的。
修正一下上文中22题给的解法。
似乎推理还推不出来。
编程计算我提的也是不对的。
应该是首先构造所有合法的可能性。
然后对于A猜不出。那么对于可能可能的B,C的组合应该是大于1种A。于是可以去掉一种的。
同样的对去掉后的,根据B猜不出,可以去掉一些。
再根据C继续去掉。
最后A猜出了,说明对应的B,C组合有只有一种情况。
我但是算出来是有四种情况。
于是尝试修改,对于B,C的组合,不考虑其顺序的话,还剩两种情况。
得再想想。
不考虑顺序,还剩0种。
56.最长公共字串。
经典lcs dp
57.用俩个栈实现队列。
似乎也没啥说的
58.从尾到头输出链表。
似乎可以考虑递归。
也可以考虑临时性翻转。
还可以考虑把值存到一个序列中去。
59.不能被继承的类。
final类的经典实现:利用一个private虚继承一个有非平凡构造函数的类。
60.在O(1)时间内删除链表结点。
写的时候要小心。
61.找出数组中两个只出现一次的数字
可以先全部异或起来,得到这两个数字的异或值。
可以知道这两个数字在某一位上不同,根据这个不同,把所有的数字分为两组。
分组异或出来为所求。
类似问题,1到n的数,丢失了一个数,如何求出来。丢失了两个呢?
62.找出链表的第一个公共结点。
似乎没啥说的。
一个以前我给的答案,遍历三次(遍历的时候返转),得到
A + X, B + X, A + B的值,(A为每一个链表独立部分,B为第二个链接独立部分,X为公共部分)
但是这似乎要假定X > 0.
63.在字符串中删除特定的字符。
没啥说的。
64. 寻找丑数。
在一个更大的集合内BFS。
65.输出1到最大的N位数
似乎没说的。
如果要溢出的话,说明输出相当大,再去注意一些细节意义不大了。
66.颠倒栈。
直接递归地做了。
不清楚的是,输入是啥?能改变输入栈么?
67.俩个闲玩娱乐。
67.1似乎直接排序就完了。
67.2假定n不太大,用dp[i][j]表示前i个骰子组合成j的方案数。
于是加一个骰子可以更新dp[i+1][j+x] x = 1 ... 6。
如果n太大,可以试着把生成函数求出来。
68.把数组排成最小的数。
对于两个串a,b。a在b的前面的时候a+b<b+a.
69.旋转数组中的最小元素。
似乎可以2分的。在前面的题目中有类似的。
70.给出一个函数来输出一个字符串的所有排列。
http://hi.baidu.com/feixue/blog/item/9442d11337eef9085aaf5355.html
71.数值的整数次方。
二分
72.
singleton的实现方法太多,但是各种实现又有各种问题。
73.对策字符串的最大长度。
最长回文子串:
经典方法:反转后连接到原字符串上,求出后缀数组,再求出高度数组,再各种处理。
另外还有一个,基于分治,类似暴力,近似线性的做法。
74.数组中超过出现次数超过一半的数字
主元素的查找,一种做法是每两个一组,不同的消去,相同的保留一个,最后还是线性的。
另一种做法是扫描+计数。
扩展:允许刚好出现一半。
75.二叉树两个结点的最低共同父结点
经典的LCA问题。
在欧拉序列上做RMQ。
或者用tarjan离线地做。
或者直接暴力。
76.复杂链表的复制
A B A B A B
77.关于链表问题的面试题目如下:
77.1似乎old了
在chinaunix有一个04年9月的贴子,里面有分析,似乎比较详细。
77.2又old了。
77.3还是没变。
77.4略
77.5略
78.链表和数组的区别在哪里?
各有长短。
有一种互补的数据结构叫 块状链表。
79.
80.阿里巴巴一道笔试题
似乎是我发的贴子里的。
81
81.1
用一个数组表示所有后缀的最小值,然后从左往右扫描,记录扫描到的最大值。
81.2
反向做hash?
81.3
一般是rbt。
82
82.1
不熟悉这方面的
82.2
同上
83
83.1
统计奇数的数组,然后两个位置开始扫描,都有不合法的时候交换。
83.2
old题。
84
84.1
一般还是开个数组扫描并统计
84.2
如果n是偶数可以知道一半的概率大于等于n/2于是可以用随机的0,1表示,再加上一个0到n/2-1的随机
数就行了。
如果是奇数似乎我没有好的想法,可以考虑生成一个0到2^t-1的随机数然后对n取模,可以知道取模后可能
的值都是1/n,当t越大,效果越好。这样可以以1/n的概率返回n/2,对于其它数很好处理。
85
85.1翻转A后的最长公共前缀。
85.2单串匹配算法灰常多的。
86
这个递归地用用就行了,平衡的话,要溢出时整数的个数就已经溢出了。
非递归的话开个指针数组,一次长度为2,处理的地址是0,2,4第二次长度为4地址是0,4,8。
87
似乎都没什么可以说的。
88
暂时我只能做到O(n)空间O(n)时间或者O(1)空间O(n^2)时间。
89
89.5
表示只会用后缀数组求最大公共子串。
90
90.1
似乎是在考察无中间变量的交换。
90.2
while (str[i] = str[j++]) if (str[i] != key) ++i;
90.3
略
91
91.1
10:第桶酒给对应的二进制位那些老鼠吃。
91.2
不清楚输入输出
92
经典的逆序数了
93
和前文重复了。
94
如果数据范围不大,可以先排序,然后从大的往小的扫描:
dp[i][j]表示以i结尾,公差为j的最长序列,时空复杂度和元素范围有关。
范围太大的话,可以考虑搜索。
95
略
96
略
97
略
98
略
99
99.1
从两头开始点可以计算出半个小时,组合多个可以计算出15分钟。
99.2
略
99.3
如果我问指向的一条路是不是正确的方向,对方会回答什么。
100
略
ps1,倒推。
ps2,还在想。
完。
=============
欢迎,各位,毫不犹豫的,对他的思路、或解法提出质疑、批评、指正。谢谢。
友情链接下:
飞雪主页:
http://hi.csdn.net/baihacker
飞雪博客:
http://blog.csdn.net/baihacker
--------------------------------------------------
接下来,我会陆续贴出其它网友在我帖子上,所回复的精彩答案与思路。
再次,向飞雪等网友表示致敬。
谢谢,大家。
帖子回复光荣榜第一期(按回复先后顺序排列):
感谢:飞雪
shmiluwabi666
My_hello
mimo9527
hawksoft
涂文强
litaoye
fengqiao1999
linyt
Force200413
supernove
kof87427
特别感谢:
飞雪
mimo9527
litaoye
hawksoft
微软等100题系列V0.1版之三:栈、堆、队列面试题集锦
[整理III]微软等100题系列V0.1版之三:栈、堆、队列面试题集锦
July
==============
2.设计包含min函数的栈。
定义栈的数据结构,要求添加一个min函数,能够得到栈的最小元素。
要求函数min、push以及pop的时间复杂度都是O(1)。
29.栈的push、pop序列
题目:输入两个整数序列。其中一个序列表示栈的push顺序,
判断另一个序列有没有可能是对应的pop顺序。
为了简单起见,我们假设push序列的任意两个整数都是不相等的。
比如输入的push序列是1、2、3、4、5,那么4、5、3、2、1就有可能是一个pop系列。
因为可以有如下的push和pop序列:
push 1,push 2,push 3,push 4,pop,push 5,pop,pop,pop,pop,
这样得到的pop序列就是4、5、3、2、1。
但序列4、3、5、1、2就不可能是push序列1、2、3、4、5的pop序列。
34.
实现一个队列。
队列的应用场景为:
一个生产者线程将int类型的数入列,一个消费者线程将int类型的数出列
35.
求一个矩阵中最大的二维矩阵(元素和最大).如:
1 2 0 3 4
2 3 4 5 1
1 1 5 3 0
中最大的是:
4 5
5 3
要求:(1)写出算法;(2)分析时间复杂度;(3)用C写出关键代码
57.用俩个栈实现队列。
题目:某队列的声明如下:
template<typename T> class CQueue
{
public:
CQueue() {}
~CQueue() {}
void appendTail(const T& node); // append a element to tail
void deleteHead(); // remove a element from head
private:
T> m_stack1;
T> m_stack2;
};
分析:从上面的类的声明中,我们发现在队列中有两个栈。
因此这道题实质上是要求我们用两个栈来实现一个队列。
相信大家对栈和队列的基本性质都非常了解了:栈是一种后入先出的数据容器,
因此对队列进行的插入和删除操作都是在栈顶上进行;队列是一种先入先出的数据容器,
我们总是把新元素插入到队列的尾部,而从队列的头部删除元素。
66.颠倒栈。
题目:用递归颠倒一个栈。例如输入栈{1, 2, 3, 4, 5},1在栈顶。
颠倒之后的栈为{5, 4, 3, 2, 1},5处在栈顶。
经典算法研究系列:一、A*搜索算法
作者:July、二零一一年一月
更多请参阅:十三个经典算法研究与总结、目录+索引。
----------------------------------
博主说明:
1、本经典算法研究系列,此系列文章写的不够好之处,还望见谅。
2、本经典算法研究系列,系我参考资料,一篇一篇原创所作,转载必须注明作者本人July及出处。
3、本经典算法研究系列,精益求精,不断优化,永久更新,永久勘误。
欢迎,各位,与我一同学习探讨,交流研究。
有误之处,不吝指正。
-------------------------------------------
引言
1968年,的一篇论文,“P. E. Hart, N. J. Nilsson, and B. Raphael. A formal basis for the heuristic determination of minimum cost paths in graphs. IEEE Trans. Syst. Sci. and Cybernetics, SSC-4(2):100-107, 1968”。从此,一种精巧、高效的算法------A*算法横空出世了,并在相关领域得到了广泛的应用。
启发式搜索算法
要理解A*搜寻算法,还得从启发式搜索算法开始谈起。
所谓启发式搜索,就在于当前搜索结点往下选择下一步结点时,可以通过一个启发函数来进行选择,选择代价最少的结点作为下一步搜索结点而跳转其上(遇到有一个以上代价最少的结点,不妨选距离当前搜索点最近一次展开的搜索点进行下一步搜索)。
DFS和BFS在展开子结点时均属于盲目型搜索,也就是说,它不会选择哪个结点在下一次搜索中更优而去跳转到该结点进行下一步的搜索。在运气不好的情形中,均需要试探完整个解集空间, 显然,只能适用于问题规模不大的搜索问题中。
而与DFS,BFS不同的是,一个经过仔细设计的启发函数,往往在很快的时间内就可得到一个搜索问题的最优解,对于NP问题,亦可在多项式时间内得到一个较优解。是的,关键就是如何设计这个启发函数。
A*搜寻算法
A*搜寻算法,俗称A星算法,作为启发式搜索算法中的一种,这是一种在图形平面上,有多个节点的路径,求出最低通过成本的算法。常用于游戏中的NPC的移动计算,或线上游戏的BOT的移动计算上。该算法像Dijkstra算法一样,可以找到一条最短路径;也像BFS一样,进行启发式的搜索。
A*算法最为核心的部分,就在于它的一个估值函数的设计上:
f(n)=g(n)+h(n)
其中f(n)是每个可能试探点的估值,它有两部分组成:
一部分,为g(n),它表示从起始搜索点到当前点的代价(通常用某结点在搜索树中的深度来表示)。
另一部分,即h(n),它表示启发式搜索中最为重要的一部分,即当前结点到目标结点的估值,
h(n)设计的好坏,直接影响着具有此种启发式函数的启发式算法的是否能称为A*算法。
一种具有f(n)=g(n)+h(n)策略的启发式算法能成为A*算法的充分条件是:
1、搜索树上存在着从起始点到终了点的最优路径。
2、问题域是有限的。
3、所有结点的子结点的搜索代价值>0。
4、h(n)=<h*(n) (h*(n)为实际问题的代价值)。
当此四个条件都满足时,一个具有f(n)=g(n)+h(n)策略的启发式算法能成为A*算法,并一定能找到最优解。
对于一个搜索问题,显然,条件1,2,3都是很容易满足的,而条件4: h(n)<=h*(n)是需要精心设计的,由于h*(n)显然是无法知道的,所以,一个满足条件4的启发策略h(n)就来的难能可贵了。
不过,对于图的最优路径搜索和八数码问题,有些相关策略h(n)不仅很好理解,而且已经在理论上证明是满足条件4的,从而为这个算法的推广起到了决定性的作用。
且h(n)距离h*(n)的呈度不能过大,否则h(n)就没有过强的区分能力,算法效率并不会很高。对一个好的h(n)的评价是:h(n)在h*(n)的下界之下,并且尽量接近h*(n)。
A*搜寻算法的实现
先举一个小小的例子:即求V0->V5的路径,V0->V5的过程中,可以经由V1,V2,V3,V4各点达到目的点V5。下面的问题,即是求此起始顶点V0->途径任意顶点V1、V2、V3、V4->目标顶点V5的最短路径。
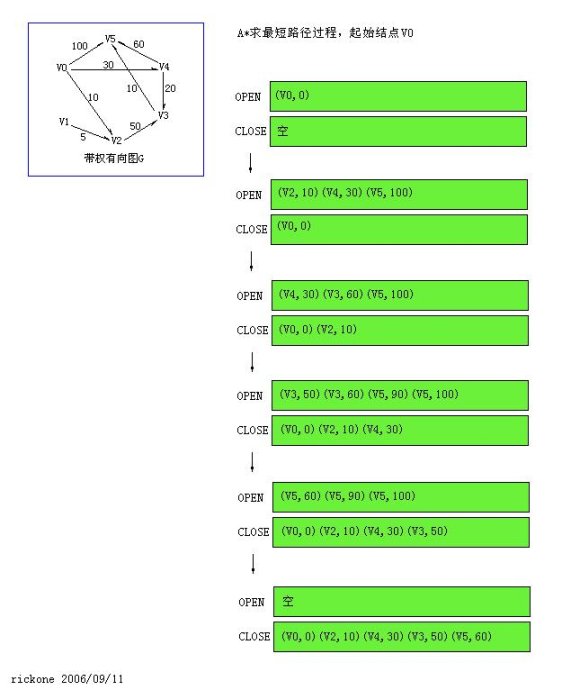
//图片是引用rickone 的。上图中,说白了,无非就是:一个队列,open 往close 插入元素。
通过上图,我们可以看出::A*算法最为核心的过程,就在每次选择下一个当前搜索点时,是从所有已探知的但未搜索过点中(可能是不同层,亦可不在同一条支路上),选取f值最小的结点进行展开。
而所有“已探知的但未搜索过点”可以通过一个按f值升序的队列(即优先队列)进行排列。
这样,在整体的搜索过程中,只要按照类似广度优先的算法框架,从优先队列中弹出队首元素(f值),对其可能子结点计算g、h和f值,直到优先队列为空(无解)或找到终止点为止。
A*算法与广度、深度优先和Dijkstra 算法的联系就在于:当g(n)=0时,该算法类似于DFS,当h(n)=0时,该算法类似于BFS。且同时,如果h(n)为0,只需求出g(n),即求出起点到任意顶点n的最短路径,则转化为单源最短路径问题,即Dijkstra算法。这一点,可以通过上面的A*搜索树的具体过程中将h(n)设为0或将g(n)设为0而得到。
A*算法流程:
首先将起始结点S放入OPEN表,CLOSE表置空,算法开始时:
1、如果OPEN表不为空,从表头取一个结点n,如果为空算法失败。
2、n是目标解吗?是,找到一个解(继续寻找,或终止算法)。
3、将n的所有后继结点展开,就是从n可以直接关联的结点(子结点),如果不在CLOSE表中,就将它们放入OPEN表,并把S放入CLOSE表,同时计算每一个后继结点的估价值f(n),将OPEN表按f(x)排序,最小的放在表头,重复算法,回到1。
//OPEN-->CLOSE,起点-->任意顶点g(n)-->目标顶点h(n)
closedset := the empty set //已经被估算的节点集合
openset := set containing the initial node //将要被估算的节点集合
g_score[start] := 0 //g(n)
h_score[start] := heuristic_estimate_of_distance(start, goal) //h(n)
f_score[start] := h_score[start]
while openset is not empty //若OPEN表不为空
x := the node in openset having the lowest f_score[] value //x为OPEN表中最小的
if x = goal //如果x是一个解
return reconstruct_path(came_from,goal) //
remove x from openset
add x to closedset //x放入
CLSOE表
for each y in neighbor_nodes(x)
if y in closedset
continue
tentative_g_score := g_score[x] + dist_between(x,y)
if y not in openset
add y to openset
tentative_is_better := true
else if tentative_g_score < g_score[y]
tentative_is_better := true
else
tentative_is_better := false
if tentative_is_better = true
came_from[y] := x
g_score[y] := tentative_g_score
h_score[y] := heuristic_estimate_of_distance(y, goal) //x-->y-->goal
f_score[y] := g_score[y] + h_score[y]
return failure
function reconstruct_path(came_from,current_node)
if came_from[current_node] is set
p = reconstruct_path(came_from,came_from[current_node])
return (p + current_node)
else
return the empty path
与结点写在一起的数值表示那个结点的价值f(n),当OPEN表为空时CLOSE表中将求得从V0到其它所有结点的最短路径。
考虑到算法性能,外循环中每次从OPEN表取一个元素,共取了n次(共n个结点),每次展开一个结点的后续结点时,需O(n)次,同时再对OPEN表做一次排序,OPEN表大小是O(n)量级的,若用快排就是O(nlogn),乘以外循环总的复杂度是O(n^2 * logn),
如果每次不是对OPEN表进行排序,因为总是不断地有新的结点添加进来,所以不用进行排序,而是每次从OPEN表中求一个最小的,那只需要O(n)的复杂度,所以总的复杂度为O(n*n),这相当于Dijkstra算法。
本文完。
July、二零一一年二月十日更新。
------------------------------------------------
后续:July、二零一一年三月一日更新。
简述A*最短路径算法的方法:
目标:从当前位置A到目标位置B找到一条最短的行走路径。
方法:从A点开始,遍历所有的可走路径,记录到一个结构中,记录内容为(位置点,最小步数)
当任何第二次走到一个点的时候,判断最小步骤是否小于记录的内容,如果是,则更新掉原最小步数,一直到所有的路径点都不能继续都了为止,最终那个点被标注的最小步数既是最短路径,
而反向找跟它相连的步数相继少一个值的点连起来就形成了最短路径,当多个点相同,则任意取一条即可。
总结:
A*算法实际是个穷举算法,也与课本上教的最短路径算法类似。课本上教的是两头往中间走,也是所有路径都走一次,每一个点标注最短值。(更多,请参考此A*搜寻算法的后续一篇文章:一(续)、A*,Dijkstra,BFS算法性能比较及A*算法的应用。谢谢大家。)本文完。
记2个月来,我在Csdn 掀起的微软面试风暴
2010年冬风暴来袭:记2个月来,我在Csdn 掀起的面试风暴
---年初的纪念与新年祝福
作者: July
时间:2013年年初
----------------------------------------------
2010年10月11日,是个值得我个人纪念的日子。那天,我正式注册了Csdn,并当天在论坛上,
发表了第一篇帖子,那个帖子 便是引起后来在Csdn 掀起一股狂热风暴的微软等面试100题系列的第一篇帖子,
标题为:算法面试:精选微软经典的算法面试100题 [每周更新]。
当时的想法很简单:我既然手头上搜集到了这么多好的、经典的面试题,那就把它,分享出来给大家共同享用吧。
与此同时,还能看到大家的 思路火一样的碰撞。。更能扩宽自己的视野。
如此美妙的事,何乐而不为列?
说干就干。于是,微软等面试100题系列首次在Csdn 亮相了。
其实,在此之前,我当时并未把Csdn 当做这100题系列发表的首选,
只是后来在Csdn看到越来越多的热心、实力的网友,才更加坚定了我想不断发表下去的决心。
刚开始的时候,有不少人表示是并不支持与赞同的。不过,到底是坚持下来了,
并最终完整发完了微软等面试100题系列V0.1版的全部100题(参见博客其它文章)。
不管怎样,作为此微软等100题系列的第一篇帖子,一经发表,整理公布,很快,
就有越来越多的人,看到,并参与做题中来。点击率持续 直线上升。
每天看着不少网友独特而绝妙的思路,心里,既新鲜又美妙。
但就在11天后,虽然,陆陆续续还是有不少的网友在帖子上,回复自己的思路,我结贴了。
因为,我发现,这微软100题系列,影响了我正常的学习,我不喜欢受到外来过多的干扰。
所以,我说,我要走了。
但第二天,2010年10月23日,我就 come back,发表了此微软100题系列的第二篇帖子。
[推荐] [整理]算法面试:精选微软经典的算法面试100题[前40题](第二篇帖子)
到底是因为这个东西还没有完成,我不能搁置弃在一旁,所以,又回来了。
在第二篇帖子上,我整理了我自己、和网友们在我第一篇帖子上回复的思路,版面干净了不少。
终于,帖子后来 被十一文 推荐了。
自此,不但点击率急剧攀升,几乎每个注意留意论坛的人,都能见到这第二篇帖子了。
与此同时,在网友lovesi3344的提醒下,我陆续把这100题系列上传了资源,
于是,资源被推荐,也一下子火了起来,网友们对资源评论:“感谢”“感谢楼主分享”“好人啊,感谢分享”。。。
我意识到了,我做了一件 对大家有利的好事。但我始终不认为我是个好人 :)。
我仅仅 只是做了一件分享的小事而已。
终于渐渐的,我意识到了这微软等100题所隐含的巨大潜力,每天看着那么多的人,来看帖,回帖,
内心里有股莫名其妙的兴奋劲儿。一天网上,寝室熄灯后,潜意识里告知我,
应该写一篇关于这微软等100题系列的文章。结果,那晚我一挥而就。
于是,第二天,2010年11月17日,一篇名为 横空出世,席卷Csdn [评微软等公司数据结构+算法面试100题]
的文章在我博客上发表了。发表后几天,我本想还删了此篇文章的。
大概7天后,这篇文章 终被推荐了,上CSDN 首页了,博客精选第二条,那时,甭提有多兴奋了。
终于,仅仅 一个多月的时间,我在CSDN 掀起了一股面试风暴。
我觉得自己做了一件非常有意义非常值得分享的事。
正如那篇文章里所提到的:“这100道题,不仅解决了大量初学者找不到编程素材、练习资料的尴尬,
而且更是给你最直接的诱惑:
作者随后直接亲自参与做这100题,或自个做,或引用他人方案,一步步带你思考,一步步挖代码给你看。
作者在展示自己和他人思考成果的同时,给他人带来了无比重要的分享,此举颇有开源精神。”
而后我博客里又接连 第二篇 第三篇文章被推荐,
主题全是有关这100题系列的(详情请参考本博客其它文章)。
直到2010年12月6日,随着此篇文章发表:
[珍藏版]微软等数据结构+算法面试100题全部出炉[100题V0.1版完美汇总]
微软等数据结构+算法面试100题系列,全部的100题终于全部发完了。
那天,长吁了一口气,我到底是坚持下来了。
100题,首先是我一个人在默默的做,然后发展到上千网友,一起与我来做。
我知道这在整个CSDN ,也是非常罕见且难得的事。
但毕竟,整理这100题,所要花费的时间和精力太大了。但有时想到,我的这一举动,
能给上万参加 面试的朋友、毕业生,一解燃眉之急,又给初学者带来了大量的经典编程素材,
同时还为他们 提供整理答案,想到这,不觉,又来了劲。
无论如何,这微软等100题系列,已告一段落,虽然剩下60题的答案还未整理公布。
但,无须急,明年2011年,与微软等面试100题系列V0.2版 一起整理公布吧。
这股面试风暴还远未停息,明年,它将继续来袭。:D。
谢谢,所有关注本微软等面试100题系列V0.1版的,所有网友、朋友。
2010年即将告别,2011年的钟声即将敲起。
祝各位、度过一个新鲜快乐、无比祥和的新春佳节。
祝各位 在新的一年里,一顺百顺,事事顺利,人人健康。
祝自己,所有的心愿 都能在接下来的日子里,一一全部实现。
经典算法研究系列:二、Dijkstra 算法初探
经典算法研究系列:二、Dijkstra 算法初探
July 二零一一年一月
本文主要参考:算法导论 第二版、维基百科。
一、Dijkstra 算法的介绍
Dijkstra 算法,又叫迪科斯彻算法(Dijkstra),算法解决的是有向图中单个源点到其他顶点的最短路径问题。举例来说,如果图中的顶点表示城市,而边上的权重表示著城市间开车行经的距离,Dijkstra 算法可以用来找到两个城市之间的最短路径。
二、图文解析 Dijkstra 算法
ok,经过上文有点繁杂的信息,你还并不对此算法了如指掌,清晰透彻。没关系,咱们来幅图,就好了。请允许我再对此算法的概念阐述下,
Dijkstra算法是典型最短路径算法,用于计算一个节点到其他所有节点的最短路径。不过,针对的是非负值权边。主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。[Dijkstra算法能得出最短路径的最优解,但由于它遍历计算的节点很多,所以效率低。]
ok,如下图,设A为源点,求A到其他各所有一一顶点(B、C、D、E、F)的最短路径。线上所标注为相邻线段之间的距离,即权值。
(注:此图为随意所画,其相邻顶点间的距离与图中的目视长度不能一一对等)
Dijkstra无向图
算法执行步骤如下表:
三、Dijkstra 的算法实现
Dijkstra 算法的输入包含了一个有权重的有向图 G,以及G中的一个来源顶点 S。我们以 V 表示 G 中所有顶点的集合,以 E 表示G 中所有边的集合。
(u, v) 表示从顶点 u 到 v 有路径相连,而边的权重则由权重函数 w: E → [0, ∞] 定义。因此,w(u, v) 就是从顶点 u 到顶点 v 的非负花费值(cost),边的花费可以想像成两个顶点之间的距离。
任两点间路径的花费值,就是该路径上所有边的花费值总和。
已知有 V 中有顶点 s 及 t,Dijkstra 算法可以找到 s 到 t 的最低花费路径(例如,最短路径)。这个算法也可以在一个图中,找到从一个顶点 s 到任何其他顶点的最短路径。
好,咱们来看下此算法的具体实现:
Dijkstra 算法的实现一(维基百科):
u := Extract_Min(Q) 在顶点集合 Q 中搜索有最小的 d[u] 值的顶点 u。这个顶点被从集合 Q 中删除并返回给用户。
1 function Dijkstra(G, w, s)
2 for each vertex v in V[G] // 初始化
3 d[v] := infinity
4 previous[v] := undefined
5 d[s] := 0
6 S := empty set
7 Q := set of all vertices
8 while Q is not an empty set // Dijkstra演算法主體
9 u := Extract_Min(Q)
10 S := S union {u}
11 for each edge (u,v) outgoing from u
12 if d[v] > d[u] + w(u,v) // 拓展边(u,v)
13 d[v] := d[u] + w(u,v)
14 previous[v] := u
如果我们只对在 s 和 t 之间寻找一条最短路径的话,我们可以在第9行添加条件如果满足 u = t 的话终止程序。现在我们可以通过迭代来回溯出 s 到 t 的最短路径:
1 s := empty sequence
2 u := t
3 while defined u
4 insert u to the beginning of S
5 u := previous[u]
现在序列 S 就是从 s 到 t 的最短路径的顶点集.
Dijkstra 算法的实现二(算法导论):
DIJKSTRA(G, w, s)
1 INITIALIZE-SINGLE-SOURCE(G, s)
2 S ← Ø
3 Q ← V[G] //V*O(1)
4 while Q ≠ Ø
5 do u ← EXTRACT-MIN(Q) //EXTRACT-MIN,V*O(V),V*O(lgV)
6 S ← S ∪{u}
7 for each vertex v ∈ Adj[u]
8 do RELAX(u, v, w) //松弛技术,E*O(1),E*O(lgV)。
因为Dijkstra算法总是在V-S中选择“最轻”或“最近”的顶点插入到集合S中,所以我们说它使用了贪心策略。
(贪心算法会在日后的博文中详细阐述)。
二零一一年二月九日更新:
此Dijkstra 算法的最初的时间复杂度为O(V*V+E),源点可达的话,O(V*lgV+E*lgV)=>O(E*lgV)
当是稀疏图的情况时,E=V*V/lgV,算法的时间复杂度可为O(V^2)。
但我们知道,若是斐波那契堆实现优先队列的话,算法时间复杂度,则为O(V*lgV + E)。
四、Dijkstra 算法的执行速度
我们可以用大O符号将Dijkstra 算法的运行时间表示为边数 m 和顶点数 n 的函数。Dijkstra 算法最简单的实现方法是用一个链表或者数组来存储所有顶点的集合 Q,所以搜索 Q 中最小元素的运算(Extract-Min(Q))只需要线性搜索 Q 中的所有元素。这样的话算法的运行时间是 O(E^2)。
对于边数少于 E^2 的稀疏图来说,我们可以用邻接表来更有效的实现迪科斯彻算法。同时需要将一个二叉堆或者斐波纳契堆用作优先队列来寻找最小的顶点(Extract-Min)。
当用到二叉堆时候,算法所需的时间为O(( V+E )logE),斐波纳契堆能稍微提高一些性能,让算法运行时间达到O(V+ElogE)。(此处一月十六日修正。)
开放最短路径优先(OSPF, Open Shortest Path First)算法是迪科斯彻算法在网络路由中的一个具体实现。
与 Dijkstra 算法不同,Bellman-Ford算法可用于具有负数权值边的图,只要图中不存在总花费为负值且从源点 s 可达的环路即可用此算法(如果有这样的环路,则最短路径不存在,因为沿环路循环多次即可无限制的降低总花费)。
与最短路径问题相关最有名的一个问题是旅行商问题(Traveling salesman problem),此类问题要求找出恰好通过所有标点一次且最终回到原点的最短路径。
然而该问题为NP-完全的;换言之,与最短路径问题不同,旅行商问题不太可能具有多项式时间解法。如果有已知信息可用来估计某一点到目标点的距离,则可改用A*搜寻算法,以减小最短路径的搜索范围。
二零一一年二月九日更新:
BFS、DFS、Kruskal、Prim、Dijkstra算法时间复杂度的比较:
一般说来,我们知道,BFS,DFS算法的时间复杂度为O(V+E),
最小生成树算法Kruskal、Prim算法的时间复杂度为O(E*lgV)。
而Prim算法若采用斐波那契堆实现的话,算法时间复杂度为O(E+V*lgV),当|V|<<|E|时,E+V*lgV是一个较大的改进。
//|V|<<|E|,=>O(E+V*lgV) << O(E*lgV),对吧。:D
Dijkstra 算法,斐波纳契堆用作优先队列时,算法时间复杂度为O(V*lgV + E)。
//看到了吧,与Prim算法采用斐波那契堆实现时,的算法时间复杂度是一样的。
所以我们,说,BFS、Prime、Dijkstra 算法是有相似之处的,单从各算法的时间复杂度比较看,就可窥之一二。
==============================================
此文,写的实在不怎么样。不过,承蒙大家厚爱,此经典算法研究系列的后续文章,个人觉得写的还行。
所以,还请,各位可关注此算法系列的后续文章。谢谢。
二零一一年一月四日。
教你透彻了解红黑树
教你透彻了解红黑树
本文参考:Google、算法导论、STL源码剖析、计算机程序设计艺术。
推荐阅读:Left-Leaning Red-Black Trees, Dagstuhl Workshop on Data Structures, Wadern, Germany, February, 2008.
直接下载:http://www.cs.princeton.edu/~rs/talks/LLRB/RedBlack.pdf
------------------------------
红黑树系列,六篇文章于今日已经完成:
------------------------------
一、红黑树的介绍
先来看下算法导论对R-B Tree的介绍:
红黑树,一种二叉查找树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。
通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的。
前面说了,红黑树,是一种二叉查找树,既然是二叉查找树,那么它必满足二叉查找树的一般性质。
下面,在具体介绍红黑树之前,咱们先来了解下 二叉查找树的一般性质:
1.在一棵二叉查找树上,执行查找、插入、删除等操作,的时间复杂度为O(lgn)。
因为,一棵由n个结点,随机构造的二叉查找树的高度为lgn,所以顺理成章,一般操作的执行时间为O(lgn)。
//至于n个结点的二叉树高度为lgn的证明,可参考算法导论 第12章 二叉查找树 第12.4节。
2.但若是一棵具有n个结点的线性链,则此些操作最坏情况运行时间为O(n)。
而红黑树,能保证在最坏情况下,基本的动态几何操作的时间均为O(lgn)。
ok,我们知道,红黑树上每个结点内含五个域,color,key,left,right,p。如果相应的指针域没有,则设为NIL。
一般的,红黑树,满足以下性质,即只有满足以下全部性质的树,我们才称之为红黑树:
1)每个结点要么是红的,要么是黑的。
2)根结点是黑的。
3)每个叶结点(叶结点即指树尾端NIL指针或NULL结点)是黑的。
4)如果一个结点是红的,那么它的俩个儿子都是黑的。
5)对于任一结点而言,其到叶结点树尾端NIL指针的每一条路径都包含相同数目的黑结点。
(注:上述第3、5点性质中所说的NULL结点,包括wikipedia.算法导论上所认为的叶子结点即为树尾端的NIL指针,或者说NULL结点。然百度百科以及网上一些其它博文直接说的叶结点,则易引起误会,因,此叶结点非子结点)
如下图所示,即是一颗红黑树(下图引自wikipedia:http://t.cn/hgvH1l):

此图忽略了叶子和根部的父结点。同时,上文中我们所说的 "叶结点" 或"NULL结点",如上图所示,它不包含数据而只充当树在此结束的指示,这些节点在绘图中经常被省略,望看到此文后的读者朋友注意。
二、树的旋转知识
当我们在对红黑树进行插入和删除等操作时,对树做了修改,那么可能会违背红黑树的性质。
为了保持红黑树的性质,我们可以通过对树进行旋转,即修改树种某些结点的颜色及指针结构,以达到对红黑树进行插入、删除结点等操作时,红黑树依然能保持它特有的性质(如上文所述的,五点性质)。
树的旋转,分为左旋和右旋,以下借助图来做形象的解释和介绍:
1.左旋
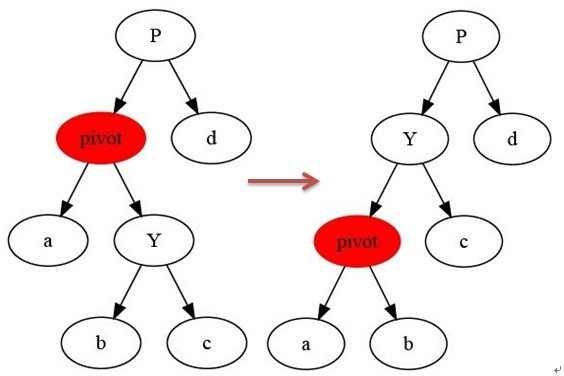
如上图所示:
当在某个结点pivot上,做左旋操作时,我们假设它的右孩子y不是NIL[T],pivot可以为树内任意右孩子而不是NIL[T]的结点。
左旋以pivot到y之间的链为“支轴”进行,它使y成为该孩子树新的根,而y的左孩子b则成为pivot的右孩子。
来看算法导论对此操作的算法实现(以x代替上述的pivot):
- LEFT-ROTATE(T, x)
- 1 y ← right[x] ▹ Set y.
- 2 right[x] ← left[y] ▹ Turn y's left subtree into x's right subtree.
- 3 p[left[y]] ← x
- 4 p[y] ← p[x] ▹ Link x's parent to y.
- 5 if p[x] = nil[T]
- 6 then root[T] ← y
- 7 else if x = left[p[x]]
- 8 then left[p[x]] ← y
- 9 else right[p[x]] ← y
- 10 left[y] ← x ▹ Put x on y's left.
- 11 p[x] ← y
2.右旋
右旋与左旋差不多,再此不做详细介绍。

对于树的旋转,能保持不变的只有原树的搜索性质,而原树的红黑性质则不能保持,在红黑树的数据插入和删除后可利用旋转和颜色重涂来恢复树的红黑性质。
至于有些书如 STL源码剖析有对双旋的描述,其实双旋只是单旋的两次应用,并无新的内容,因此这里就不再介绍了,而且左右旋也是相互对称的,只要理解其中一种旋转就可以了。
三、红黑树插入、删除操作的具体实现
I、ok,接下来,咱们来具体了解红黑树的插入操作。
向一棵含有n个结点的红黑树插入一个新结点的操作可以在O(lgn)时间内完成。
算法导论:
- RB-INSERT(T, z)
- 1 y ← nil[T]
- 2 x ← root[T]
- 3 while x ≠ nil[T]
- 4 do y ← x
- 5 if key[z] < key[x]
- 6 then x ← left[x]
- 7 else x ← right[x]
- 8 p[z] ← y
- 9 if y = nil[T]
- 10 then root[T] ← z
- 11 else if key[z] < key[y]
- 12 then left[y] ← z
- 13 else right[y] ← z
- 14 left[z] ← nil[T]
- 15 right[z] ← nil[T]
- 16 color[z] ← RED
- 17 RB-INSERT-FIXUP(T, z)
咱们来具体分析下,此段代码:
RB-INSERT(T, z),将z插入红黑树T 之内。
为保证红黑性质在插入操作后依然保持,上述代码调用了一个辅助程序RB-INSERT-FIXUP来对结点进行重新着色,并旋转。
14 left[z] ← nil[T]
15 right[z] ← nil[T] //保持正确的树结构
第16行,将z着为红色,由于将z着为红色可能会违背某一条红黑树的性质,
所以,在第17行,调用RB-INSERT-FIXUP(T,z)来保持红黑树的性质。
RB-INSERT-FIXUP(T, z),如下所示:
- 1 while color[p[z]] = RED
- 2 do if p[z] = left[p[p[z]]]
- 3 then y ← right[p[p[z]]]
- 4 if color[y] = RED
- 5 then color[p[z]] ← BLACK ▹ Case 1
- 6 color[y] ← BLACK ▹ Case 1
- 7 color[p[p[z]]] ← RED ▹ Case 1
- 8 z ← p[p[z]] ▹ Case 1
- 9 else if z = right[p[z]]
- 10 then z ← p[z] ▹ Case 2
- 11 LEFT-ROTATE(T, z) ▹ Case 2
- 12 color[p[z]] ← BLACK ▹ Case 3
- 13 color[p[p[z]]] ← RED ▹ Case 3
- 14 RIGHT-ROTATE(T, p[p[z]]) ▹ Case 3
- 15 else (same as then clause
- with "right" and "left" exchanged)
- 16 color[root[T]] ← BLACK
ok,参考一网友的言论,用自己的语言,再来具体解剖下上述俩段代码。
为了保证阐述清晰,我再写下红黑树的5个性质:
1)每个结点要么是红的,要么是黑的。
2)根结点是黑的。
3)每个叶结点,即空结点(NIL)是黑的。
4)如果一个结点是红的,那么它的俩个儿子都是黑的。
5)对每个结点,从该结点到其子孙结点的所有路径上包含相同数目的黑结点。
在对红黑树进行插入操作时,我们一般总是插入红色的结点,因为这样可以在插入过程中尽量避免对树的调整。
那么,我们插入一个结点后,可能会使原树的哪些性质改变列?
由于,我们是按照二叉树的方式进行插入,因此元素的搜索性质不会改变。
如果插入的结点是根结点,性质2会被破坏,如果插入结点的父结点是红色,则会破坏性质4。
因此,总而言之,插入一个红色结点只会破坏性质2或性质4。
我们的回复策略很简单,
其一、把出现违背红黑树性质的结点向上移,如果能移到根结点,那么很容易就能通过直接修改根结点来恢复红黑树的性质。直接通过修改根结点来恢复红黑树应满足的性质。
其二、穷举所有的可能性,之后把能归于同一类方法处理的归为同一类,不能直接处理的化归到下面的几种情况,
//注:以下情况3、4、5与上述算法导论上的代码RB-INSERT-FIXUP(T, z),相对应:
插入修复具体操作情况
情况1:插入的是根结点。
原树是空树,此情况只会违反性质2。
对策:直接把此结点涂为黑色。
情况2:插入的结点的父结点是黑色。
此不会违反性质2和性质4,红黑树没有被破坏。
对策:什么也不做。
情况3:当前结点的父结点是红色且祖父结点的另一个子结点(叔叔结点)是红色。
此时父结点的父结点一定存在,否则插入前就已不是红黑树。
与此同时,又分为父结点是祖父结点的左子还是右子,对于对称性,我们只要解开一个方向就可以了。
在此,我们只考虑父结点为祖父左子的情况。
同时,还可以分为当前结点是其父结点的左子还是右子,但是处理方式是一样的。我们将此归为同一类。
对策:将当前节点的父节点和叔叔节点涂黑,祖父结点涂红,把当前结点指向祖父节点,从新的当前节点重新开始算法。
针对情况3,变化前(图片来源:saturnman)[当前节点为4节点]:
变化后:
情况4:当前节点的父节点是红色,叔叔节点是黑色,当前节点是其父节点的右子
对策:当前节点的父节点做为新的当前节点,以新当前节点为支点左旋。
如下图所示,变化前[当前节点为7节点]:
变化后:
情况5:当前节点的父节点是红色,叔叔节点是黑色,当前节点是其父节点的左子
解法:父节点变为黑色,祖父节点变为红色,在祖父节点为支点右旋
如下图所示[当前节点为2节点]
变化后:
「回顾:经过上面情况3、情况4、情况5等3种插入修复情况的操作示意图,读者自会发现,后面的情况4、情况5都是针对情况3插入节点4以后,进行的一系列插入修复情况操作,不过,指向当前节点N指针一直在变化。所以,你可以想当然的认为:整个下来,情况3、4、5就是一个完整的插入修复情况的操作流程」
II、ok,接下来,咱们最后来了解,红黑树的删除操作:
为了保证以下的介绍与阐述清晰,我第三次重写下红黑树的5个性质
1)每个结点要么是红的,要么是黑的。
2)根结点是黑的。
3)每个叶结点,即空结点(NIL)是黑的。
4)如果一个结点是红的,那么它的俩个儿子都是黑的。
5)对每个结点,从该结点到其子孙结点的所有路径上包含相同数目的黑结点。
(相信,重述了3次,你应该有深刻记忆了。:D)
"我们删除的节点的方法与常规二叉搜索树中删除节点的方法是一样的,如果被删除的节点不是有双非空子女,则直接删除这个节点,用它的唯一子节点顶替它的位置,如果它的子节点分是空节点,那就用空节点顶替它的位置,如果它的双子全为非空,我们就把它的直接后继节点内容复制到它的位置,之后以同样的方式删除它的后继节点,它的后继节点不可能是双子非空,因此此传递过程最多只进行一次。”
继续讲解之前,补充说明下二叉树结点删除的几种情况,待删除的节点按照儿子的个数可以分为三种:
2、只有一个儿子。那么把父结点的相应儿子指针指向儿子的独生子,删除儿子结点也OK了。
3、有两个儿子。这是最麻烦的情况,因为你删除节点之后,还要保证满足搜索二叉树的结构。其实也比较容易,我们可以选择左儿子中的最大元素或者右儿子中的最小元素放到待删除节点的位置,就可以保证结构的不变。当然,你要记得调整子树,毕竟又出现了节点删除。习惯上大家选择左儿子中的最大元素,其实选择右儿子的最小元素也一样,没有任何差别,只是人们习惯从左向右。这里咱们也选择左儿子的最大元素,将它放到待删结点的位置。左儿子的最大元素其实很好找,只要顺着左儿子不断的去搜索右子树就可以了,直到找到一个没有右子树的结点。那就是最大的了。
OK,回到红黑树上来。算法导论一书,给的红黑树结点删除的算法实现是:
RB-DELETE(T, z) 单纯删除结点的总操作
- 1 if left[z] = nil[T] or right[z] = nil[T]
- 2 then y ← z
- 3 else y ← TREE-SUCCESSOR(z)
- 4 if left[y] ≠ nil[T]
- 5 then x ← left[y]
- 6 else x ← right[y]
- 7 p[x] ← p[y]
- 8 if p[y] = nil[T]
- 9 then root[T] ← x
- 10 else if y = left[p[y]]
- 11 then left[p[y]] ← x
- 12 else right[p[y]] ← x
- 13 if y 3≠ z
- 14 then key[z] ← key[y]
- 15 copy y's satellite data into z
- 16 if color[y] = BLACK
- 17 then RB-DELETE-FIXUP(T, x)
- 18 return y
“在删除节点后,原红黑树的性质可能被改变,如果删除的是红色节点,那么原红黑树的性质依旧保持,此时不用做修正操作,如果删除的节点是黑色节点,原红黑树的性质可能会被改变,我们要对其做修正操作。那么哪些树的性质会发生变化呢,如果删除节点不是树唯一节点,那么删除节点的那一个支的到各叶节点的黑色节点数会发生变化,此时性质5被破坏。如果被删节点的唯物主唯一非空子节点是红色,而被删节点的父节点也是红色,那么性质4被破坏。如果被删节点是根节点,而它的唯一非空子节点是红色,则删除后新根节点将变成红色,违背性质2。”
RB-DELETE-FIXUP(T, x) 恢复与保持红黑性质的工作
- 1 while x ≠ root[T] and color[x] = BLACK
- 2 do if x = left[p[x]]
- 3 then w ← right[p[x]]
- 4 if color[w] = RED
- 5 then color[w] ← BLACK ▹ Case 1
- 6 color[p[x]] ← RED ▹ Case 1
- 7 LEFT-ROTATE(T, p[x]) ▹ Case 1
- 8 w ← right[p[x]] ▹ Case 1
- 9 if color[left[w]] = BLACK and color[right[w]] = BLACK
- 10 then color[w] ← RED ▹ Case 2
- 11 x p[x] ▹ Case 2
- 12 else if color[right[w]] = BLACK
- 13 then color[left[w]] ← BLACK ▹ Case 3
- 14 color[w] ← RED ▹ Case 3
- 15 RIGHT-ROTATE(T, w) ▹ Case 3
- 16 w ← right[p[x]] ▹ Case 3
- 17 color[w] ← color[p[x]] ▹ Case 4
- 18 color[p[x]] ← BLACK ▹ Case 4
- 19 color[right[w]] ← BLACK ▹ Case 4
- 20 LEFT-ROTATE(T, p[x]) ▹ Case 4
- 21 x ← root[T] ▹ Case 4
- 22 else (same as then clause with "right" and "left" exchanged)
- 23 color[x] ← BLACK
“上面的修复情况看起来有些复杂,下面我们用一个分析技巧:我们从被删节点后来顶替它的那个节点开始调整,并认为它有额外的一重黑色。这里额外一重黑色是什么意思呢,我们不是把红黑树的节点加上除红与黑的另一种颜色,这里只是一种假设,我们认为我们当前指向它,因此空有额外一种黑色,可以认为它的黑色是从它的父节点被删除后继承给它的,它现在可以容纳两种颜色,如果它原来是红色,那么现在是红+黑,如果原来是黑色,那么它现在的颜色是黑+黑。有了这重额外的黑色,原红黑树性质5就能保持不变。现在只要花时是恢复其它性质就可以了,做法还是尽量向根移动和穷举所有可能性。"--saturnman。
红黑树删除修复操作的几种情况@saturnman:
(注:以下的情况3、4、5、6,与上述算法导论之代码RB-DELETE-FIXUP(T, x) 恢复与保持
中case1,case2,case3,case4相对应。)
解法,直接把当前节点染成黑色,结束。
此时红黑树性质全部恢复。
情况2:当前节点是黑+黑且是根节点
解法:什么都不做,结束
情况3:当前节点是黑+黑且兄弟节点为红色(此时父节点和兄弟节点的子节点分为黑)。
解法:把父节点染成红色,把兄弟结点染成黑色,之后重新进入算法(我们只讨论当前节点是其父节点左孩子时的情况)。此变换后原红黑树性质5不变,而把问题转化为兄弟节点为黑色的情况( 注 :变化前,原本就未违反性质5,只是为了 把问题转化为兄弟节点为黑色的情况 )。
3.变化前:
3.变化后:
情况4:当前节点是黑加黑且兄弟是黑色且兄弟节点的两个子节点全为黑色。
解法:把当前节点和兄弟节点中抽取一重黑色追加到父节点上,把父节点当成新的当前节点,重新进入算法。(此变换后性质5不变)
4.变化前
4.变化后
情况5:当前节点颜色是黑+黑,兄弟节点是黑色,兄弟的左子是红色,右子是黑色。。
解法:把兄弟结点染红,兄弟左子节点染黑,之后再在兄弟节点为支点解右旋,之后重新进入算法。此是把当前的情况转化为情况6,而性质5得以保持。
5.变化前:
5.变化后:
情况6:当前节点颜色是黑-黑色,它的兄弟节点是黑色,但是兄弟节点的右子是红色,兄弟节点左子的颜色任意。
解法:把兄弟节点染成当前节点父节点的颜色,把当前节点父节点染成黑色,兄弟节点右子染成黑色,之后以当前节点的父节点为支点进行左旋,此时算法结束,红黑树所有性质调整正确。
6.变化前:
6.变化后:
限于篇幅,不再过多赘述。更多,可参考算法导论或下文我写的第二篇文章。完。
July、二零一零年十二月二十九日初稿。三十日凌晨修订。
----------------
今下午画红黑树画了好几个钟头,贴俩张图:
红黑树插入修复的3种情况:
红黑树删除修复的4种情况:
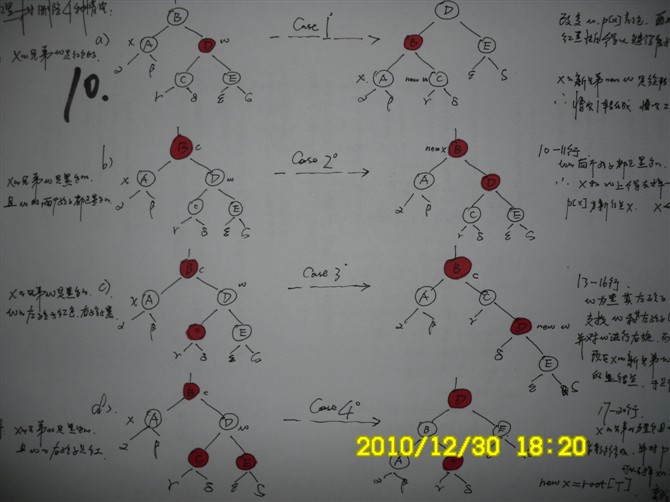
ok,只贴俩张,更多,参考我写的关于红黑树的第二篇文章:
红黑树算法的层层剖析与逐步实现[推荐]
微软等100题系列V0.1版:字符串+数组面试题集锦
微软等100题系列V1.0版整理IV:字符串+数组面试题集锦
July 2010年12月30日
第4章 字符串+数组面试题
在微软等100题系列V0.1版中,此类字符串+数组的问题,占了足足22道。
可见 字符串+数组等基础问题之重要性。
接下来的俩天,我会加快分类整理完100题系列V0.1版,然后加紧整理完网友的答案回复,
最后,我挑选其中最为经典的几道题,直接在博客上贴出源码、答案。
为了迎接在2011年元旦之际,微软等数据结构+算法面试100题系列V0.2版的出炉。
请继续保持关注。谢谢。:D。July、十二月三十日。
[分类整理I]微软等100题系列V0.1版:c/c++基础面试题集锦
http://blog.csdn.net/v_JULY_v/archive/2010/12/14/6076111.aspx
[分类整理II]微软等100题系列V0.1版:链表面试题集锦
http://blog.csdn.net/v_JULY_v/archive/2010/12/14/6076139.aspx
[分类整理III]微软等100题系列V0.1版之三:栈、堆、队列面试题集锦
http://blog.csdn.net/v_JULY_v/archive/2010/12/17/6083098.aspx
--------------------------------
3.求子数组的最大和
题目:
输入一个整形数组,数组里有正数也有负数。
数组中连续的一个或多个整数组成一个子数组,每个子数组都有一个和。
求所有子数组的和的最大值。要求时间复杂度为O(n)。
例如输入的数组为1, -2, 3, 10, -4, 7, 2, -5,和最大的子数组为3, 10, -4, 7, 2,
因此输出为该子数组的和18。
第10题
翻转句子中单词的顺序。
题目:输入一个英文句子,翻转句子中单词的顺序,但单词内字符的顺序不变。
句子中单词以空格符隔开。为简单起见,标点符号和普通字母一样处理。
例如输入“I am a student.”,则输出“student. a am I”。
第14题:
题目:输入一个已经按升序排序过的数组和一个数字,
在数组中查找两个数,使得它们的和正好是输入的那个数字。
要求时间复杂度是O(n)。如果有多对数字的和等于输入的数字,输出任意一对即可。
例如输入数组1、2、4、7、11、15和数字15。由于4+11=15,因此输出4和11。
第17题:
题目:在一个字符串中找到第一个只出现一次的字符。如输入abaccdeff,则输出b。
分析:这道题是2006年google的一道笔试题。
第20题:
题目:输入一个表示整数的字符串,把该字符串转换成整数并输出。
例如输入字符串"345",则输出整数345。
第25题:
写一个函数,它的原形是int continumax(char *outputstr,char *intputstr)
功能:
在字符串中找出连续最长的数字串,并把这个串的长度返回,
并把这个最长数字串付给其中一个函数参数outputstr所指内存。
例如:"abcd12345ed125ss123456789"的首地址传给intputstr后,函数将返回9,
outputstr所指的值为123456789
26.左旋转字符串
题目:
定义字符串的左旋转操作:把字符串前面的若干个字符移动到字符串的尾部。
如把字符串abcdef左旋转2位得到字符串cdefab。请实现字符串左旋转的函数。
要求时间对长度为n的字符串操作的复杂度为O(n),辅助内存为O(1)。
37.
有n个长为m+1的字符串,
如果某个字符串的最后m个字符与某个字符串的前m个字符匹配,则两个字符串可以联接,
问这n个字符串最多可以连成一个多长的字符串,如果出现循环,则返回错误。
45.雅虎:
1.对于一个整数矩阵,存在一种运算,对矩阵中任意元素加一时,需要其相邻(上下左右)
某一个元素也加一,现给出一正数矩阵,判断其是否能够由一个全零矩阵经过上述运算得到。
2.一个整数数组,长度为n,将其分为m份,使各份的和相等,求m的最大值
比如{3,2,4,3,6} 可以分成{3,2,4,3,6} m=1;
{3,6}{2,4,3} m=2
{3,3}{2,4}{6} m=3 所以m的最大值为3
48.微软:
一个数组是由一个递减数列左移若干位形成的,比如{4,3,2,1,6,5}
是由{6,5,4,3,2,1}左移两位形成的,在这种数组中查找某一个数。
51.和为n连续正数序列。
题目:输入一个正数n,输出所有和为n连续正数序列。
例如输入15,由于1+2+3+4+5=4+5+6=7+8=15,所以输出3个连续序列1-5、4-6和7-8。
分析:这是网易的一道面试题。
53.字符串的排列。
题目:输入一个字符串,打印出该字符串中字符的所有排列。
例如输入字符串abc,则输出由字符a、b、c所能排列出来的所有字符串
abc、acb、bac、bca、cab和cba。
分析:这是一道很好的考查对递归理解的编程题,
因此在过去一年中频繁出现在各大公司的面试、笔试题中。
54.调整数组顺序使奇数位于偶数前面。
题目:输入一个整数数组,调整数组中数字的顺序,使得所有奇数位于数组的前半部分,
所有偶数位于数组的后半部分。要求时间复杂度为O(n)。
56.最长公共字串。
题目:如果字符串一的所有字符按其在字符串中的顺序出现在另外一个字符串二中,
则字符串一称之为字符串二的子串。
注意,并不要求子串(字符串一)的字符必须连续出现在字符串二中。
请编写一个函数,输入两个字符串,求它们的最长公共子串,并打印出最长公共子串。
例如:输入两个字符串BDCABA和ABCBDAB,字符串BCBA和BDAB都是是它们的最长公共子串,
则输出它们的长度4,并打印任意一个子串。
分析:求最长公共子串(Longest Common Subsequence, LCS)是一道非常经典的动态规划题,
因此一些重视算法的公司像MicroStrategy都把它当作面试题。
63.在字符串中删除特定的字符。
题目:输入两个字符串,从第一字符串中删除第二个字符串中所有的字符。
例如,输入”They are students.”和”aeiou”,
则删除之后的第一个字符串变成”Thy r stdnts.”。
分析:这是一道微软面试题。在微软的常见面试题中,与字符串相关的题目占了很大的一部分,
因为写程序操作字符串能很好的反映我们的编程基本功。
69.旋转数组中的最小元素。
题目:把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。输入一个排好序的数组的一个旋转,
输出旋转数组的最小元素。例如数组{3, 4, 5, 1, 2}为{1, 2, 3, 4, 5}的一个旋转,该数组的最小值为1。
分析:这道题最直观的解法并不难。从头到尾遍历数组一次,就能找出最小的元素,
时间复杂度显然是O(N)。但这个思路没有利用输入数组的特性,我们应该能找到更好的解法。
73.对策字符串的最大长度。
题目:输入一个字符串,输出该字符串中对称的子字符串的最大长度。
比如输入字符串“google”,由于该字符串里最长的对称子字符串是“goog”,因此输出4。
分析:可能很多人都写过判断一个字符串是不是对称的函数,这个题目可以看成是该函数的加强版。
85.又见字符串的问题
1.给出一个函数来复制两个字符串A和B。
字符串A的后几个字节和字符串B的前几个字节重叠。
分析:记住,这种题目往往就是考你对边界的考虑情况。
2.已知一个字符串,比如asderwsde,寻找其中的一个子字符串比如sde的个数,
如果没有返回0,有的话返回子字符串的个数。
88.2005年11月金山笔试题。编码完成下面的处理函数。
函数将字符串中的字符'*'移到串的前部分,
前面的非'*'字符后移,但不能改变非'*'字符的先后顺序,函数返回串中字符'*'的数量。
如原始串为:ab**cd**e*12,
处理后为*****abcde12,函数并返回值为5。(要求使用尽量少的时间和辅助空间)
93.在一个int数组里查找这样的数,它大于等于左侧所有数,小于等于右侧所有数。
直观想法是用两个数组a、b。a[i]、b[i]分别保存从前到i的最大的数和从后到i的最小的数,
一个解答:这需要两次遍历,然后再遍历一次原数组,
将所有data[i]>=a[i-1]&&data[i]<=b[i]的data[i]找出即可。
给出这个解答后,面试官有要求只能用一个辅助数组,且要求少遍历一次。
94.微软笔试题
求随机数构成的数组中找到长度大于=3的最长的等差数列9 d- x' W) w9 ?" o3 b0 R
输出等差数列由小到大:
如果没有符合条件的就输出
格式:
输入[1,3,0,5,-1,6]
输出[-1,1,3,5]
要求时间复杂度,空间复杂度尽量小
96.08年中兴校园招聘笔试题
1.编写strcpy 函数
已知strcpy 函数的原型是
char *strcpy(char *strDest, const char *strSrc);
其中strDest 是目的字符串,strSrc 是源字符串。
不调用C++/C 的字符串库函数,请编写函数 strcpy。
----------------
1.关于本微软等公司数据结构+算法面试100题系列V0.1版的郑重声明
http://blog.csdn.net/v_JULY_v/archive/2010/12/02/6050133.aspx
2.完整100题,请参见,
[珍藏版]微软等数据结构+算法面试100题全部出炉[100题首次完整亮相]
http://blog.csdn.net/v_JULY_v/archive/2010/12/06/6057286.aspx
3.更多详情,请参见,本人博客:
My Blog:
http://blog.csdn.net/v_JULY_v
4.所有的资源(题目+答案)下载地址:
http://v_july_v.download.csdn.net/
5.本微软等100题系列V0.1版,永久维护(网友,思路回复)地址:
http://topic.csdn.net/u/20101126/10/b4f12a00-6280-492f-b785-cb6835a63dc9.html
有问题,欢迎留言或来信。联系方式,见本博客公告栏。
作者声明:
本人July对本博客所有任何内容和资料享有版权,转载请注明作者本人July及出处。
永远,向您的厚道致敬。谢谢。July、二零一零年十二月三十日。
微软等数据结构+算法面试100题系列之网友精彩回复 [二]
作者:July mimo9527
完整100题,请参见,
[珍藏版]微软等数据结构+算法面试100题全部出炉[100题首次完整亮相]
http://blog.csdn.net/v_JULY_v/archive/2010/12/06/6057286.aspx
以下所有的思路、答案选自网友mimo9527和我个人在这帖子上的回复:
本微软等100题系列V0.1版,永久维护(网友,思路回复)地址:
http://topic.csdn.net/u/20101126/10/b4f12a00-6280-492f-b785-cb6835a63dc9.html
继续欢迎,各位把自己针对此100题中任何一道,给出自己的思路,回复于上述帖子上,或于本博客上留言。:D。
========
为了表示对mimo9527的尊重,我尽量不对他的回复做修改与改动。
且尽量只贴思路,少或不贴代码。文末附上我个人对部分题、简单的思路回复。
欢迎,各位,毫不犹豫的,对以下的思路、或解法提出质疑、批评、指正。谢谢。
---------------------------------
mimo9527:
第8 题
此贴选一些比较怪的题,,由于其中题目本身与算法关系不大,仅考考思维。特此并作一题
1.非常有名的老题
2。 7= 1+2+4
3。
★假设你有一个用1001 个整数组成的数组,这些整数是任意排列的,但是你知道所有
的整数都在1 到1000(包括1000)之间。此外,除一个数字出现两次外,其他所有数字只出
现一次。假设你只能对这个数组做一次处理,用一种算法找出重复的那个数字。如果你在运
算中使用了辅助的存储方式,那么你能找到不用这种方式的算法吗?
★不用乘法或加法增加8 倍。现在用同样的方法增加7 倍。
-----------------------------------
重复的那个数字 = 数组之和 - 500500(1到1000之和)
8 倍:左移3位
7倍: 8倍-1倍
第10 题
翻转句子中单词的顺序。
题目:输入一个英文句子,翻转句子中单词的顺序,但单词内字符的顺序不变。
句子中单词以空格符隔开。为简单起见,标点符号和普通字母一样处理。
例如输入“I am a student.”,则输出“student. a am I”。
-----------------------
分析:
可以利用堆栈后进先出的特性,把输入先push到堆栈中,然后再pop出来,即反序。
第12 题
题目:求1+2+…+n,
要求不能使用乘除法、for、while、if 、else、switch、case 等关键字以及条件判断语句(A?B:C)
-----------------------------------
分析:
主要是能周期性的执行某一语句就可以了;
如启动一个周期性定时器之类的,每次超时调用一次;只是还没找到合适的定时器函数;
。。。。。。。。。
34.
实现一个队列。
队列的应用场景为:
一个生产者线程将int类型的数入列,一个消费者线程将int类型的数出列。
生产者消费者问题答案代码,有几个问题,
1。是生产和消费线程没有做互斥,如队列就是一个共享资源,需要互斥使用。
2。sleep没有必要。
3。WaitForMultipleObjects(2, handles, TRUE, INFINITE);应该没有用吧?
这位哥们,指的是我之前上传的资源,答案V0.3版关于第34题的答案。
47.创新工场:
求一个数组的最长递减子序列
比如{9,4,3,2,5,4,3,2}的最长递减子序列为{9,5,4,3,2}
-------------
分析:
相当于寻找和“9876543210”的公共子串,可以使用《算法导论》中的“最长公共子序列算法”。
-------------
前面没考虑数字大于10的情况,数字大于10的时候,不能直接作为字符串处理,而应该作为一个数组序列
,需要对程序做一点调整。
56.最长公共字串。
题目:如果字符串一的所有字符按其在字符串中的顺序出现在另外一个字符串二中,
则字符串一称之为字符串二的子串。
注意,并不要求子串(字符串一)的字符必须连续出现在字符串二中。
请编写一个函数,输入两个字符串,求它们的最长公共子串,并打印出最长公共子串。
例如:输入两个字符串BDCABA 和ABCBDAB,字符串BCBA 和BDAB 都是是它们的最
长公共子串,
则输出它们的长度4,并打印任意一个子串。
分析:求最长公共子串(Longest Common Subsequence, LCS)是一道非常经典的动态规划题,
因此一些重视算法的公司像MicroStrategy 都把它当作面试题。
-----------
与上楼相同,两个字符串BDCABA 和ABCBDAB都是《算法导论》例子里面的。。。。
void LongestCommonSubsequence()
{
char acStringX[]="abractyeyt";
char acStringY[]="dgdsaeactyey";
char acStringTemp[MAX_STRING_LEN];
int iStringXLen = strlen(acStringX);
int iStringYLen = strlen(acStringY);
int iStringTempLen;
if (iStringXLen >= MAX_STRING_LEN-1 ||iStringXLen >= MAX_STRING_LEN-1)
{
printf("string is too long!/n");
return;
}
memset(gaiComSubseqLen,0,MAX_STRING_LEN*MAX_STRING_LEN*sizeof(int));
LCS_Length(acStringX,acStringY);
LSC_Print(acStringX,iStringXLen,iStringYLen);
printf("/n");
return;
}
--------------------------
57.用俩个栈实现队列。
题目:某队列的声明如下:
template<typename T> class CQueue
{
public:
CQueue() {}
~CQueue() {}
void appendTail(const T& node); // append a element to tail
void deleteHead(); // remove a element from head
private:
T> m_stack1;
T> m_stack2;
};
分析:从上面的类的声明中,我们发现在队列中有两个栈。
因此这道题实质上是要求我们用两个栈来实现一个队列。
相信大家对栈和队列的基本性质都非常了解了:栈是一种后入先出的数据容器,
因此对队列进行的插入和删除操作都是在栈顶上进行;队列是一种先入先出的数据容器,
我们总是把新元素插入到队列的尾部,而从队列的头部删除元素。
-----------------------
分析:
这个自能是游戏,一点用也没有。
appendTail()简单,直接push到m_stack1中;
deleteHead():
pop m_stack1的每一个元素并push到m_stack2,但最后一个因为要删除不需要push到m_stack2,
然后再pop m_stack2的每一个元素并push到m_stack1。
这个过程画图比较清晰。
60.在O(1)时间内删除链表结点。
题目:给定链表的头指针和一个结点指针,在O(1)时间删除该结点。链表结点的定义如下:
struct ListNode
{
int m_nKey;
ListNode* m_pNext;
};
函数的声明如下:
void DeleteNode(ListNode* pListHead, ListNode* pToBeDeleted);
分析:这是一道广为流传的Google 面试题,能有效考察我们的编程基本功,
还能考察我们的反应速度,更重要的是,还能考察我们对时间复杂度的理解。
-----------------------
分析:
pToBeDeleted为尾节点或唯一节点时,比较简单;
否则,因为是单向链表,找不到pToBeDeleted的上一个节点,故删除比较麻烦,
所以可以将pToBeDeleted的下一个节点的内容复制到pToBeDeleted中,然后把pToBeDeleted的下一个节点删除。
62.找出链表的第一个公共结点。
题目:两个单向链表,找出它们的第一个公共结点。
链表的结点定义为:
struct ListNode
{
int m_nKey;
ListNode* m_pNext;
};
分析:这是一道微软的面试题。
微软非常喜欢与链表相关的题目,因此在微软的面试题中,链表出现的概率相当高。
-----------------------
分析:
两个链表公共节点之后的部分是完全相同的。因此从后往前找比较高效,但是单向链表做不到,
故将两个链表转换成2个数组,从2个数组的末尾开始一一对应比较,最后一个相同的点就是公共节点。
64. 寻找丑数。
题目:我们把只包含因子2、3 和5 的数称作丑数(Ugly Number)。
例如6、8 都是丑数,但14 不是,因为它包含因子7。习惯上我们把1 当做是第一个丑数。
求按从小到大的顺序的第1500 个丑数。
-----------------------
分析:
丑数=2^i*3^j*5^k(^表示多少次方),通过变换i,j,k的取值来计算;
但是我没有找到i,j,k如何取值的规律,只能不停的判断谁大谁小了。
65.输出1 到最大的N 位数
题目:输入数字n,按顺序输出从1 最大的n 位10 进制数。
比如输入3,则输出1、2、3 一直到最大的3 位数即999。
分析:这是一道很有意思的题目。看起来很简单,其实里面却有不少的玄机。
-----------------
循环长度为10的n次方,在循环之前把这个长度计算出来,别在循环里计算;
除此之外愣是没看出来有什么玄机,等待看别人的解答。
66.颠倒栈。
题目:用递归颠倒一个栈。例如输入栈{1, 2, 3, 4, 5},1 在栈顶。
颠倒之后的栈为{5, 4, 3, 2, 1},5 处在栈顶。
---------------------
分析:这个简单,
递归时把取出来的存在一个全局的数组里,然后根据要求再push回去;
pop();
存储;
判断是否是最后一个:
是:push(数组中最后一个,并在数组中删掉);
否:递归;
push(数组中最后一个,并在数组中删掉);
71.数值的整数次方。
题目:实现函数double Power(double base, int exponent),求base 的exponent 次方。
不需要考虑溢出。
-------------------------------
分析:
为了提高效率,考虑采用分治的思想:
1. 对exponent进行分解,如分解为2的i,j,k次方的和,然后对每一个递归计算;
2. 1中还有重复计算,可以增加一些处理,提高效率。
74.数组中超过出现次数超过一半的数字
题目:数组中有一个数字出现的次数超过了数组长度的一半,找出这个数字。
分析:这是一道广为流传的面试题,包括百度、微软和Google 在内的多家公司
都曾经采用过这个题目。要几十分钟的时间里很好地解答这道题,除了较好的编程能力之外,
还需要较快的反应和较强的逻辑思维能力。
----------------------------------
分析:
1. 出现次数大于数组长度N的一半的数字,一定在数组中的前一半中至少出现一次;
2. 先遍历数组的开始一半(注:如果N为奇数,则前一半多放一个),得到出现的每一个数及其出现次数的列表List;
3.开始遍历数组的后一半 FOR J=N/2; J<=N;J++:
3.1 如果是List中的数,则将List中该数出现的次数 +1;
3.2 遍历List中的每一个数:
3.2.1 如果该数出现的次数+(N-J)<=N/2,则说明该数不可能是所求数字,从List中删除该数;
3.2.1 如果该数出现的次数 > N/2,则说明该数就是所求数字;
3.3 如果List中只剩下一个数,则该数即为所求的数字;
75.二叉树两个结点的最低共同父结点
题目:二叉树的结点定义如下:
struct TreeNode
{
int m_nvalue;
TreeNode* m_pLeft;
TreeNode* m_pRight;
};
输入二叉树中的两个结点,输出这两个结点在数中最低的共同父结点。
------------------------------
分析:
进行二叉树遍历(递归),并在遍历中加入如下内容:
1.如果当前节点等于某一个输入节点,则返回1;如果不是则继续向左、右子节点遍历,如果一直到叶子节点仍未找到,则返回0;
2.如果节点的左子节点遍历和右子节点遍历都返回1,则该节点就是所求的最低的共同父结点;
80.阿里巴巴一道笔试题
引自baihacker
问题描述:
12 个高矮不同的人,排成两排,每排必须是从矮到高排列,而且第二排比对应的第一排的人高,
问排列方式有多少种?
这个笔试题,很YD,因为把某个递归关系隐藏得很深.
----------------------------
这个比较简单,思路如下:
1.从12个人中任意选取2个人出来,组成一列,根据组合数学有C(12,2)中方法;
2.再从剩余的10个人中任意选取2个人出来,组成下一列,根据组合数学有C(10,2)中方法;
3.以此类推;
4.根据组合数学的乘法原理,总的排列方式数= C(12,2)*C(10,2)*C(8,2)*C(6,2)*C(4,2)*C(2,2)=748440
5.根据上面的内容,很容易写出递归程序。
------------------------------------
结果是132,
可以抽象成将12个数填写到一个二维数组中,按从小到大的顺序填写(从大到小也一样),
填写的条件就是左边不能为空,下边不能为空。
---------------------------------------
最后附上我个人关于一些题的思路、简单回复:
July:
今天,暂写一下,前20题的,我个人的思路:
1.把二元树转化成排序的双向链表
中序遍历二元树,然后,把二元树各结点连接,转化成List。
2.设计包含min函数的栈。
这题,见的实在太多了。
我上传的答案V0.2版,已花了不少篇幅,阐述它(可参考,画个图,可能会更清晰点)。
3.求子数组的最大和
不考虑数组中全为负数的情况。
即遍历一次,就找到那些变量,然后相加。
可设俩个变量,b(数组元素为负,不加,把下一个元素赋给b,数组元素非负,相加),
sum,并始终与b比较,sum<b,则更新sum(把b赋给sum)...最后,return sum。
4.在二元树中找出和为某一值的所有路径
相当于给定一个数值,然后,在树上,找出那些结点相加的和,等于这个数值的所有结点。
还是遍历这棵二元树(递归),每访问一个叶结点,结点值相加,同时把结点进栈,
当最后的和,等于这个数值,打印此条路径。
否则,退回到父结点,出栈,重新查找。
5.查找最小的k个元素
参考答案V0.2版,上有完整源程序。
6.腾讯面试题
此题,只要找出规律后,就能很快写出下排的数。
当然,编程求解,有一定难度。请参考答案V0.3版。
7.判断俩个链表是否相交
问题转化为:
1.先判断带不带换
2.如果都不带环,判断尾结点是否相等
3.如果都带环,判断一链表上俩指针相遇的那个结点,
是否在另一条链表上。
如果在,则相交,不在,则不相交。
8.微软面试题。
此题较繁琐,略。
9.判断整数序列是不是二元查找树的后序遍历结果
考察树的后序遍历。
10.翻转句子中单词的顺序。
这题,很多人,都想到了。略。
11.求二叉树中结点的最大距离
若不清楚题意,网上搜下,看下图。
且答案V0.2版,已花了不小的篇幅阐述了此题,请参考。
12.求1+2+....n(诸多限制)
循环本质,即让同样的代码执行n次而已。
很多方法:
1.利用构造函数的特殊性质
2.模板
...
13.输出链表中倒数第k个结点
此题的思路,用俩指针,一指head,一指k-1个元素,相隔k的距离
很多人,都知道。
14.给定一个数值,查找相加的和,等于此数值的俩个数
此题与第21题差不多,但难度不及第21题。且还有序数列。
15.把树翻转,转化为它的镜像
利用递归,借助栈。
16.从上到下按层,打印树的每个结点
非树的,前、中、后序遍历,乃树的层次遍历。
利用队列(本质即是一种BFS,不知各位,是否察觉)。
其实,此题,还可以出的更难点。:D..
17.在一个字符串中找到第一个只出现一次的字符
hash表。
18.约瑟夫循环
相信,大家对这个问题,都明了,不用我啰嗦。
19.斐波拉契数列。
注意细节。略。
20.字符串转换成整数输出。
同样,注意细节问题。:D..
//下面的,待续。Copy right@July 2010年11月28日。
针对262 楼 litaoye 的回复:
26.左旋转字符串
跟panda所想,是一样的,即,
以abcdef为例
1. ab->ba
2. cdef->fedc
原字符串变为bafedc
3. 整个翻转:cdefab
//时间复杂度为O(n)
在此,奉献另外一种思路:
abc defghi,要abc移动至最后
abc defghi->def abcghi->def ghiabc
一俩指针,p1指向ch[0],p2指向[ch m-1],
p2每次移动m 的距离,p1 也跟着相应移动,
每次移动过后,交换。
如上第一步,交换abc 和def ,就变成了 abcdef->defabc
第一步,
abc defghi->def abcghi
第二步,继续交换,
def abcghi->def ghiabc
整个过程,看起来,就是abc 一步一步 向后移动
abc defghi
def abcghi
def ghi abc
//最后的 复杂度是O(m+n)
再举一个例子,
如果123 4567890要变成4567890 123:
123 4567890
1. 456 123 7890
2. 456789 123 0
3. 456789 12 0 3
4. 456789 1 0 23
5. 4567890 123 //最后三步,相当于0前移,p1已经不动。
欢迎,就此第26题,继续讨论。
40.百度研发笔试题
40.1.设计min函数的栈。
这个问题,我已经在答案V0.2,V0.3版里,讨论过很多次了。
欢迎,各位大侠,批评指正。
此题的第1小题,即是借助辅助栈,保存最小值,
且随时更新辅助栈中的元素。
如先后,push 2 6 4 1 5
stack A stack B(辅助栈)
4: 5 1 //push 5,min=p->[3]=1 ^
3: 1 1 //push 1,min=p->[3]=1 | //此刻push进A的元素1小于B中栈顶元素2
2: 4 2 //push 4,min=p->[0]=2 |
1: 6 2 //push 6,min=p->[0]=2 |
0: 2 2 //push 2,min=p->[0]=2 |
push第一个元素进A,也把它push进B,
当向Apush的元素比B中的元素小, 则也push进B,即更新B。否则,不动B,保存原值。
向栈A push元素时,顺序由下至上。
辅助栈B中,始终保存着最小的元素。
然后,pop栈A中元素,5 1 4 6 2
A B ->更新
4: 5 1 1 //pop 5,min=p->[3]=1 |
3: 1 1 2 //pop 1,min=p->[0]=2 |
2: 4 2 2 //pop 4,min=p->[0]=2 |
1: 6 2 2 //pop 6,min=p->[0]=2 |
0: 2 2 NULL //pop 2,min=NULL v
当pop A中的元素小于B中栈顶元素时,则也要pop B中栈顶元素。
40.2.一串首尾相连的珠子(m个),有N种颜色(N<=10),
设计一个算法,取出其中一段,要求包含所有N中颜色,并使长度最短。
一网友给的思路:
比如,字符集是a,b,c,字符串是abdcaabcx,则最短子串为abc
用两个变量 front,rear 指向一个的子串区间的头和尾
用一个int cnt[255]={0}记录当前这个子串里 字符集a,b,c 各自的个数,
一个变量sum记录字符集里有多少个了。
rear 一直加,更新cnt[]和sum的值,直到 sum等于字符集个数
然后front++,直到cnt[]里某个字符个数为0,这样就找到一个符合条件的字串了
继续前面的操作,就可以找到最短的了。
//http://www.gevgb.com/bbs/viewthread.php?tid=21&extra=page%3D1
40.3.欢迎,其他人,继续共享自己的思路。
49.一道看上去很吓人的算法面试题:
如何对n个数进行排序,要求时间复杂度O(n),空间复杂度O(1)
题目,没有问题,再想想。
经典算法研究系列:五、红黑树算法的实现与剖析
引言:
昨天下午画红黑树画了好几个钟头,总共10页纸。
特此,再深入剖析红黑树的算法实现,教你如何彻底实现红黑树算法。
经过我上一篇博文,“教你透彻了解红黑树”后,相信大家对红黑树已经有了一定的了解。
个人觉得,这个红黑树,还是比较容易懂的。
不论是插入、还是删除,不论是左旋还是右旋,最终的目的只有一个:
即保持红黑树的5个性质,不得违背。
再次,重述下红黑树的五个性质:
一般的,红黑树,满足一下性质,即只有满足一下性质的树,我们才称之为红黑树:
1)每个结点要么是红的,要么是黑的。
2)根结点是黑的。
3)每个叶结点,即空结点(NIL)是黑的。
4)如果一个结点是红的,那么它的俩个儿子都是黑的。
5)对每个结点,从该结点到其子孙结点的所有路径上包含相同数目的黑结点。
抓住了红黑树的那5个性质,事情就好办多了。
如,
1.红黑红黑,要么是红,要么是黑;
2.根结点是黑;
3.每个叶结点是黑;
4.一个红结点,它的俩个儿子必然都是黑的;
5.每一条路径上,黑结点的数目等同。
五条性质,合起来,来句顺口溜就是:(1)红黑 (2)黑 (3)黑 (4&5)红->黑 黑。
本文所有的文字,都是参照我昨下午画的十张纸(即我拍的照片)与算法导论来写的。
希望,你依照此文一点一点的往下看,看懂此文后,你对红黑树的算法了解程度,一定大增不少。
ok,现在咱们来具体深入剖析红黑树的算法,并教你逐步实现此算法。
此教程分为10个部分,每一个部分作为一个小节。且各小节与我给的十张照片一一对应。
一、左旋与右旋
先明确一点:为什么要左旋?
因为红黑树插入或删除结点后,树的结构发生了变化,从而可能会破坏红黑树的性质。
为了维持插入、或删除结点后的树,仍然是一颗红黑树,所以有必要对树的结构做部分调整,从而恢复红黑树的原本性质。
而为了恢复红黑性质而作的动作包括:
结点颜色的改变(重新着色),和结点的调整。
这部分结点调整工作,改变指针结构,即是通过左旋或右旋而达到目的。
从而使插入、或删除结点的树重新成为一颗新的红黑树。
ok,请看下图:

如上图所示,‘找茬’
如果你看懂了上述俩幅图有什么区别时,你就知道什么是“左旋”,“右旋”。
在此,着重分析左旋算法:
左旋,如图所示(左->右),以x->y之间的链为“支轴”进行,
使y成为该新子树的根,x成为y的左孩子,而y的左孩子则成为x的右孩子。
算法很简单,还有注意一点,各个结点从左往右,不论是左旋前还是左旋后,结点大小都是从小到大。
左旋代码实现,分三步(注意我给的注释):
The pseudocode for LEFT-ROTATE assumes that right[x] ≠ nil[T] and that the root's parent is nil[T].
LEFT-ROTATE(T, x)
1 y ← right[x] ▹ Set y.
2 right[x] ← left[y] //开始变化,y的左孩子成为x的右孩子
3 if left[y] !=nil[T]
4 then p[left[y]] <- x
5 p[y] <- p[x] //y成为x的父母
6 if p[x] = nil[T]
7 then root[T] <- y
8 else if x = left[p[x]]
9 then left[p[x]] ← y
10 else right[p[x]] ← y
11 left[y] ← x //x成为y的左孩子(一月三日修正)
12 p[x] ← y
//注,此段左旋代码,原书第一版英文版与第二版中文版,有所出入。
//个人觉得,第二版更精准。所以,此段代码以第二版中文版为准。
左旋、右旋都是对称的,且都是在O(1)时间内完成。因为旋转时只有指针被改变,而结点中的所有域都保持不变。
最后,贴出昨下午关于此左旋算法所画的图:
左旋(第2张图):

//此图有点bug。第4行的注释移到第11行。如上述代码所示。(一月三日修正)
二、左旋的一个实例
不做过多介绍,看下副图,一目了然。
LEFT-ROTATE(T, x)的操作过程(第3张图):
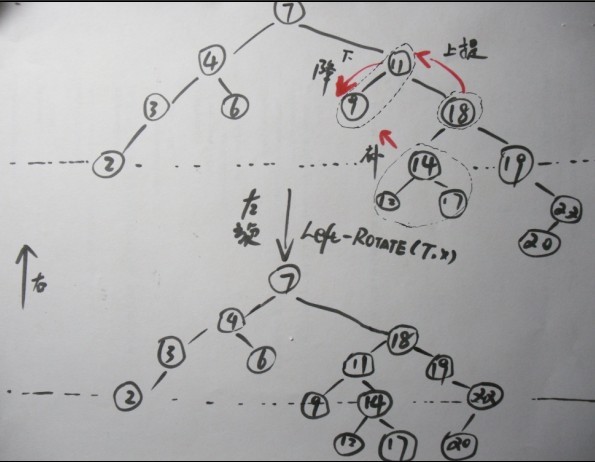
---------------------
提醒,看下文之前,请首先务必明确,区别以下俩种操作:
1.红黑树插入、删除结点的操作
//如插入中,红黑树插入结点操作:RB-INSERT(T, z)。
2.红黑树已经插入、删除结点之后,
为了保持红黑树原有的红黑性质而做的恢复与保持红黑性质的操作。
//如插入中,为了恢复和保持原有红黑性质,所做的工作:RB-INSERT-FIXUP(T, z)。
ok,请继续。
三、红黑树的插入算法实现
RB-INSERT(T, z) //注意我给的注释...
1 y ← nil[T] // y 始终指向 x 的父结点。
2 x ← root[T] // x 指向当前树的根结点,
3 while x ≠ nil[T]
4 do y ← x
5 if key[z] < key[x] //向左,向右..
6 then x ← left[x]
7 else x ← right[x] // 为了找到合适的插入点,x 探路跟踪路径,直到x成为NIL 为止。
8 p[z] ← y // y置为 插入结点z 的父结点。
9 if y = nil[T]
10 then root[T] ← z
11 else if key[z] < key[y]
12 then left[y] ← z
13 else right[y] ← z //此 8-13行,置z 相关的指针。
14 left[z] ← nil[T]
15 right[z] ← nil[T] //设为空,
16 color[z] ← RED //将新插入的结点z作为红色
17 RB-INSERT-FIXUP(T, z) //因为将z着为红色,可能会违反某一红黑性质,
//所以需要调用RB-INSERT-FIXUP(T, z)来保持红黑性质。
17 行的RB-INSERT-FIXUP(T, z) ,在下文会得到着重而具体的分析。
还记得,我开头说的那句话么,
是的,时刻记住,不论是左旋还是右旋,不论是插入、还是删除,都要记得恢复和保持红黑树的5个性质。
四、调用RB-INSERT-FIXUP(T, z)来保持和恢复红黑性质
RB-INSERT-FIXUP(T, z)
1 while color[p[z]] = RED
2 do if p[z] = left[p[p[z]]]
3 then y ← right[p[p[z]]]
4 if color[y] = RED
5 then color[p[z]] ← BLACK ▹ Case 1
6 color[y] ← BLACK ▹ Case 1
7 color[p[p[z]]] ← RED ▹ Case 1
8 z ← p[p[z]] ▹ Case 1
9 else if z = right[p[z]]
10 then z ← p[z] ▹ Case 2
11 LEFT-ROTATE(T, z) ▹ Case 2
12 color[p[z]] ← BLACK ▹ Case 3
13 color[p[p[z]]] ← RED ▹ Case 3
14 RIGHT-ROTATE(T, p[p[z]]) ▹ Case 3
15 else (same as then clause
with "right" and "left" exchanged)
16 color[root[T]] ← BLACK
//第4张图略:
五、红黑树插入的三种情况,即RB-INSERT-FIXUP(T, z)。操作过程(第5张):

//这幅图有个小小的问题,读者可能会产生误解。图中左侧所表明的情况2、情况3所标的位置都要标上一点。
//请以图中的标明的case1、case2、case3为准。一月三日。
六、红黑树插入的第一种情况(RB-INSERT-FIXUP(T, z)代码的具体分析一)
为了保证阐述清晰,重述下RB-INSERT-FIXUP(T, z)的源码:
RB-INSERT-FIXUP(T, z)
1 while color[p[z]] = RED
2 do if p[z] = left[p[p[z]]]
3 then y ← right[p[p[z]]]
4 if color[y] = RED
5 then color[p[z]] ← BLACK ▹ Case 1
6 color[y] ← BLACK ▹ Case 1
7 color[p[p[z]]] ← RED ▹ Case 1
8 z ← p[p[z]] ▹ Case 1
9 else if z = right[p[z]]
10 then z ← p[z] ▹ Case 2
11 LEFT-ROTATE(T, z) ▹ Case 2
12 color[p[z]] ← BLACK ▹ Case 3
13 color[p[p[z]]] ← RED ▹ Case 3
14 RIGHT-ROTATE(T, p[p[z]]) ▹ Case 3
15 else (same as then clause
with "right" and "left" exchanged)
16 color[root[T]] ← BLACK
//case1表示情况1,case2表示情况2,case3表示情况3.
ok,如上所示,相信,你已看到了。
咱们,先来透彻分析红黑树插入的第一种情况:
插入情况1,z的叔叔y是红色的。
第一种情况,即上述代码的第5-8行:
5 then color[p[z]] ← BLACK ▹ Case 1
6 color[y] ← BLACK ▹ Case 1
7 color[p[p[z]]] ← RED ▹ Case 1
8 z ← p[p[z]] ▹ Case 1
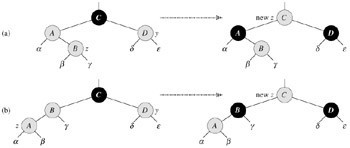
如上图所示,a:z为右孩子,b:z为左孩子。
只有p[z]和y(上图a中A为p[z],D为z,上图b中,B为p[z],D为y)都是红色的时候,才会执行此情况1.
咱们分析下上图的a情况,即z为右孩子时
因为p[p[z]],即c是黑色,所以将p[z]、y都着为黑色(如上图a部分的右边),
此举解决z、p[z]都是红色的问题,将p[p[z]]着为红色,则保持了性质5.
ok,看下我昨天画的图(第6张):
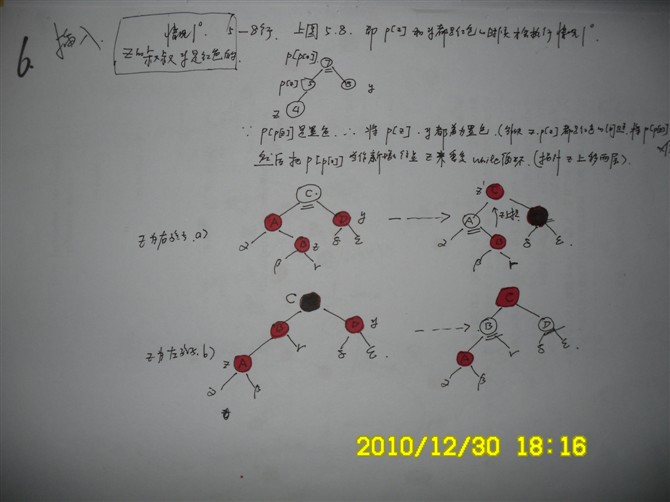
红黑树插入的第一种情况完。
七、红黑树插入的第二种、第三种情况
插入情况2:z的叔叔y是黑色的,且z是右孩子
插入情况3:z的叔叔y是黑色的,且z是左孩子
这俩种情况,是通过z是p[z]的左孩子,还是右孩子区别的。
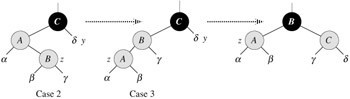
参照上图,针对情况2,z是她父亲的右孩子,则为了保持红黑性质,左旋则变为情况3,此时z为左孩子,
因为z、p[z]都为黑色,所以不违反红黑性质(注,情况3中,z的叔叔y是黑色的,否则此种情况就变成上述情况1 了)。
ok,我们已经看出来了,情况2,情况3都违反性质4(一个红结点的俩个儿子都是黑色的)。
所以情况2->左旋后->情况3,此时情况3同样违反性质4,所以情况3->右旋,得到上图的最后那部分。
注,情况2、3都只违反性质4,其它的性质1、2、3、5都不违背。
好的,最后,看下我画的图(第7张):
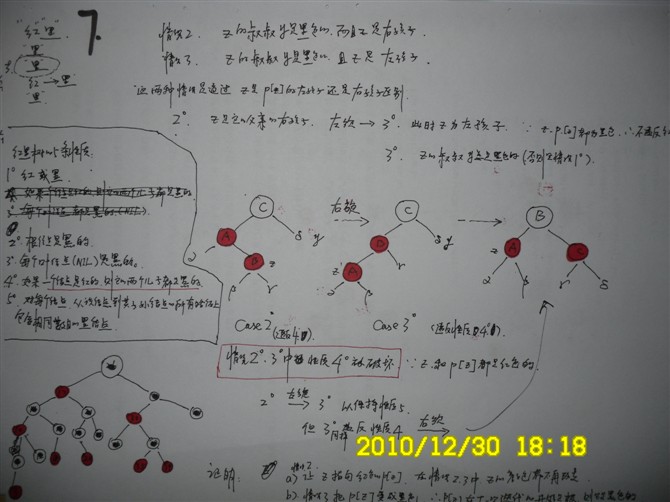
八、接下来,进入红黑树的删除部分。
RB-DELETE(T, z)
1 if left[z] = nil[T] or right[z] = nil[T]
2 then y ← z
3 else y ← TREE-SUCCESSOR(z)
4 if left[y] ≠ nil[T]
5 then x ← left[y]
6 else x ← right[y]
7 p[x] ← p[y]
8 if p[y] = nil[T]
9 then root[T] ← x
10 else if y = left[p[y]]
11 then left[p[y]] ← x
12 else right[p[y]] ← x
13 if y 3≠ z
14 then key[z] ← key[y]
15 copy y's satellite data into z
16 if color[y] = BLACK //如果y是黑色的,
17 then RB-DELETE-FIXUP(T, x) //则调用RB-DELETE-FIXUP(T, x)
18 return y //如果y不是黑色,是红色的,则当y被删除时,红黑性质仍然得以保持。不做操作,返回。
//因为:1.树种各结点的黑高度都没有变化。2.不存在俩个相邻的红色结点。
//3.因为入宫y是红色的,就不可能是根。所以,根仍然是黑色的。
ok,第8张图,不必贴了。
九、红黑树删除之4种情况,RB-DELETE-FIXUP(T, x)之代码
RB-DELETE-FIXUP(T, x)
1 while x ≠ root[T] and color[x] = BLACK
2 do if x = left[p[x]]
3 then w ← right[p[x]]
4 if color[w] = RED
5 then color[w] ← BLACK ▹ Case 1
6 color[p[x]] ← RED ▹ Case 1
7 LEFT-ROTATE(T, p[x]) ▹ Case 1
8 w ← right[p[x]] ▹ Case 1
9 if color[left[w]] = BLACK and color[right[w]] = BLACK
10 then color[w] ← RED ▹ Case 2
11 x ← p[x] ▹ Case 2
12 else if color[right[w]] = BLACK
13 then color[left[w]] ← BLACK ▹ Case 3
14 color[w] ← RED ▹ Case 3
15 RIGHT-ROTATE(T, w) ▹ Case 3
16 w ← right[p[x]] ▹ Case 3
17 color[w] ← color[p[x]] ▹ Case 4
18 color[p[x]] ← BLACK ▹ Case 4
19 color[right[w]] ← BLACK ▹ Case 4
20 LEFT-ROTATE(T, p[x]) ▹ Case 4
21 x ← root[T] ▹ Case 4
22 else (same as then clause with "right" and "left" exchanged)
23 color[x] ← BLACK
ok,很清楚,在此,就不贴第9张图了。
在下文的红黑树删除的4种情况,详细、具体分析了上段代码。
十、红黑树删除的4种情况
情况1:x的兄弟w是红色的。
情况2:x的兄弟w是黑色的,且w的俩个孩子都是黑色的。
情况3:x的兄弟w是黑色的,w的左孩子是红色,w的右孩子是黑色。
情况4:x的兄弟w是黑色的,且w的右孩子时红色的。
操作流程图:
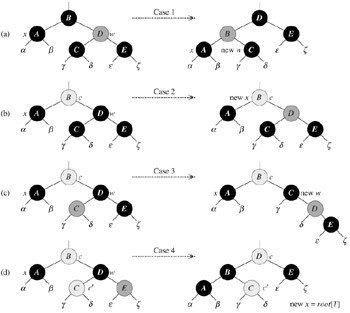
ok,简单分析下,红黑树删除的4种情况:
针对情况1:x的兄弟w是红色的。
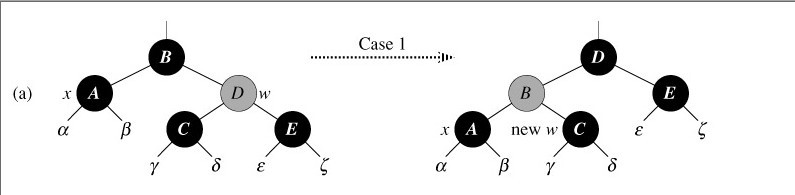
5 then color[w] ← BLACK ▹ Case 1
6 color[p[x]] ← RED ▹ Case 1
7 LEFT-ROTATE(T, p[x]) ▹ Case 1
8 w ← right[p[x]] ▹ Case 1
对策:改变w、p[z]颜色,再对p[x]做一次左旋,红黑性质得以继续保持。
x的新兄弟new w是旋转之前w的某个孩子,为黑色。
所以,情况1转化成情况2或3、4。
针对情况2:x的兄弟w是黑色的,且w的俩个孩子都是黑色的。

10 then color[w] ← RED ▹ Case 2
11 x <-p[x] ▹ Case 2
如图所示,w的俩个孩子都是黑色的,
对策:因为w也是黑色的,所以x和w中得去掉一黑色,最后,w变为红。
p[x]为新结点x,赋给x,x<-p[x]。
针对情况3:x的兄弟w是黑色的,w的左孩子是红色,w的右孩子是黑色。
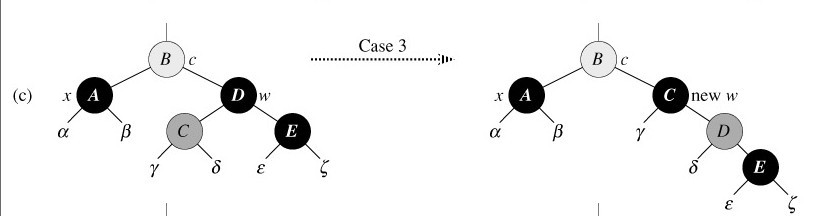
13 then color[left[w]] ← BLACK ▹ Case 3
14 color[w] ← RED ▹ Case 3
15 RIGHT-ROTATE(T, w) ▹ Case 3
16 w ← right[p[x]] ▹ Case 3
w为黑,其左孩子为红,右孩子为黑
对策:交换w和和其左孩子left[w]的颜色。 即上图的D、C颜色互换。:D。
并对w进行右旋,而红黑性质仍然得以保持。
现在x的新兄弟w是一个有红色右孩子的黑结点,于是将情况3转化为情况4.
针对情况4:x的兄弟w是黑色的,且w的右孩子时红色的。
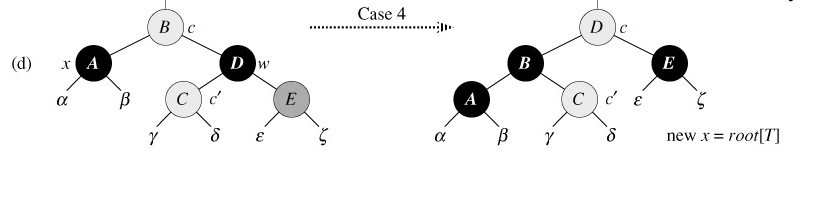
17 color[w] ← color[p[x]] ▹ Case 4
18 color[p[x]] ← BLACK ▹ Case 4
19 color[right[w]] ← BLACK ▹ Case 4
20 LEFT-ROTATE(T, p[x]) ▹ Case 4
21 x ← root[T] ▹ Case 4
x的兄弟w为黑色,且w的右孩子为红色。
对策:做颜色修改,并对p[x]做一次旋转,可以去掉x的额外黑色,来把x变成单独的黑色,此举不破坏红黑性质。
将x置为根后,循环结束。
最后,贴上最后的第10张图:

ok,红黑树删除的4中情况,分析完成。
结语:只要牢牢抓住红黑树的5个性质不放,而不论是树的左旋还是右旋,
不论是红黑树的插入、还是删除,都只为了保持和修复红黑树的5个性质而已。
顺祝各位, 元旦快乐。完。
三、动态规划算法解最长公共子序列LCS问题(2011.12.13重写)
第一部分、什么是动态规划算法
ok,咱们先来了解下什么是动态规划算法。
动态规划一般也只能应用于有最优子结构的问题。最优子结构的意思是局部最优解能决定全局最优解(对有些问题这个要求并不能完全满足,故有时需要引入一定的近似)。简单地说,问题能够分解成子问题来解决。
动态规划算法分以下4个步骤:
- 描述最优解的结构
- 递归定义最优解的值
- 按自底向上的方式计算最优解的值 //此3步构成动态规划解的基础。
- 由计算出的结果构造一个最优解。 //此步如果只要求计算最优解的值时,可省略。
好,接下来,咱们讨论适合采用动态规划方法的最优化问题的俩个要素:最优子结构性质,和子问题重叠性质。
- 最优子结构
如果问题的最优解所包含的子问题的解也是最优的,我们就称该问题具有最优子结构性质(即满足最优化原理)。意思就是,总问题包含很多个子问题,而这些子问题的解也是最优的。
- 重叠子问题
子问题重叠性质是指在用递归算法自顶向下对问题进行求解时,每次产生的子问题并不总是新问题,有些子问题会被重复计算多次。动态规划算法正是利用了这种子问题的重叠性质,对每一个子问题只计算一次,然后将其计算结果保存在一个表格中,当再次需要计算已经计算过的子问题时,只是在表格中简单地查看一下结果,从而获得较高的效率。
第二部分、动态规划算法解LCS问题
下面,咱们运用此动态规划算法解此LCS问题。有一点必须声明的是,LCS问题即最长公共子序列问题,它不要求所求得的字符在所给的字符串中是连续的(例如:输入两个字符串BDCABA和ABCBDAB,字符串BCBA和BDAB都是是它们的最长公共子序列,则输出它们的长度4,并打印任意一个子序列)。
ok,咱们马上进入面试题第56题的求解,即运用经典的动态规划算法:
2.0、LCS问题描述
56.最长公共子序列。
题目:如果字符串一的所有字符按其在字符串中的顺序出现在另外一个字符串二中,
则字符串一称之为字符串二的子串。
注意,并不要求子串(字符串一)的字符必须连续出现在字符串二中。
请编写一个函数,输入两个字符串,求它们的最长公共子串,并打印出最长公共子串。
例如:输入两个字符串BDCABA和ABCBDAB,字符串BCBA和BDAB都是是它们的最长公共子序列,则输出它们的长度4,并打印任意一个子序列。
分析:求最长公共子序列(Longest Common Subsequence, LCS)是一道非常经典的动态规划题,因此一些重视算法的公司像MicroStrategy都把它当作面试题。
事实上,最长公共子序列问题也有最优子结构性质。
记:
Xi=﹤x1,⋯,xi﹥即X序列的前i个字符 (1≤i≤m)(前缀)
Yj=﹤y1,⋯,yj﹥即Y序列的前j个字符 (1≤j≤n)(前缀)
假定Z=﹤z1,⋯,zk﹥∈LCS(X , Y)。
-
若xm=yn(最后一个字符相同),则不难用反证法证明:该字符必是X与Y的任一最长公共子序列Z(设长度为k)的最后一个字符,即有zk = xm = yn 且显然有Zk-1∈LCS(Xm-1 , Yn-1)即Z的前缀Zk-1是Xm-1与Yn-1的最长公共子序列。此时,问题化归成求Xm-1与Yn-1的LCS(LCS(X , Y)的长度等于LCS(Xm-1 , Yn-1)的长度加1)。
-
若xm≠yn,则亦不难用反证法证明:要么Z∈LCS(Xm-1, Y),要么Z∈LCS(X , Yn-1)。由于zk≠xm与zk≠yn其中至少有一个必成立,若zk≠xm则有Z∈LCS(Xm-1 , Y),类似的,若zk≠yn 则有Z∈LCS(X , Yn-1)。此时,问题化归成求Xm-1与Y的LCS及X与Yn-1的LCS。LCS(X , Y)的长度为:max{LCS(Xm-1 , Y)的长度, LCS(X , Yn-1)的长度}。
由于上述当xm≠yn的情况中,求LCS(Xm-1 , Y)的长度与LCS(X , Yn-1)的长度,这两个问题不是相互独立的:两者都需要求LCS(Xm-1,Yn-1)的长度。另外两个序列的LCS中包含了两个序列的前缀的LCS,故问题具有最优子结构性质考虑用动态规划法。
也就是说,解决这个LCS问题,你要求三个方面的东西:1、LCS(Xm-1,Yn-1)+1;2、LCS(Xm-1,Y),LCS(X,Yn-1);3、max{LCS(Xm-1,Y),LCS(X,Yn-1)}。
2.1、最长公共子序列的结构
最长公共子序列的结构有如下表示:
设序列X=<x1, x2, …, xm>和Y=<y1, y2, …, yn>的一个最长公共子序列Z=<z1, z2, …, zk>,则:
- 若xm=yn,则zk=xm=yn且Zk-1是Xm-1和Yn-1的最长公共子序列;
- 若xm≠yn且zk≠xm ,则Z是Xm-1和Y的最长公共子序列;
- 若xm≠yn且zk≠yn ,则Z是X和Yn-1的最长公共子序列。
其中Xm-1=<x1, x2, …, xm-1>,Yn-1=<y1, y2, …, yn-1>,Zk-1=<z1, z2, …, zk-1>。
2.2、子问题的递归结构
由最长公共子序列问题的最优子结构性质可知,要找出X=<x1, x2, …, xm>和Y=<y1, y2, …, yn>的最长公共子序列,可按以下方式递归地进行:当xm=yn时,找出Xm-1和Yn-1的最长公共子序列,然后在其尾部加上xm(=yn)即可得X和Y的一个最长公共子序列。当xm≠yn时,必须解两个子问题,即找出Xm-1和Y的一个最长公共子序列及X和Yn-1的一个最长公共子序列。这两个公共子序列中较长者即为X和Y的一个最长公共子序列。
由此递归结构容易看到最长公共子序列问题具有子问题重叠性质。例如,在计算X和Y的最长公共子序列时,可能要计算出X和Yn-1及Xm-1和Y的最长公共子序列。而这两个子问题都包含一个公共子问题,即计算Xm-1和Yn-1的最长公共子序列。
与矩阵连乘积最优计算次序问题类似,我们来建立子问题的最优值的递归关系。用c[i,j]记录序列Xi和Yj的最长公共子序列的长度。其中Xi=<x1, x2, …, xi>,Yj=<y1, y2, …, yj>。当i=0或j=0时,空序列是Xi和Yj的最长公共子序列,故c[i,j]=0。其他情况下,由定理可建立递归关系如下:
2.3、计算最优值
直接利用上节节末的递归式,我们将很容易就能写出一个计算c[i,j]的递归算法,但其计算时间是随输入长度指数增长的。由于在所考虑的子问题空间中,总共只有θ(m*n)个不同的子问题,因此,用动态规划算法自底向上地计算最优值能提高算法的效率。
计算最长公共子序列长度的动态规划算法LCS_LENGTH(X,Y)以序列X=<x1, x2, …, xm>和Y=<y1, y2, …, yn>作为输入。输出两个数组c[0..m ,0..n]和b[1..m ,1..n]。其中c[i,j]存储Xi与Yj的最长公共子序列的长度,b[i,j]记录指示c[i,j]的值是由哪一个子问题的解达到的,这在构造最长公共子序列时要用到。最后,X和Y的最长公共子序列的长度记录于c[m,n]中。
- Procedure LCS_LENGTH(X,Y);
- begin
- m:=length[X];
- n:=length[Y];
- for i:=1 to m do c[i,0]:=0;
- for j:=1 to n do c[0,j]:=0;
- for i:=1 to m do
- for j:=1 to n do
- if x[i]=y[j] then
- begin
- c[i,j]:=c[i-1,j-1]+1;
- b[i,j]:="↖";
- end
- else if c[i-1,j]≥c[i,j-1] then
- begin
- c[i,j]:=c[i-1,j];
- b[i,j]:="↑";
- end
- else
- begin
- c[i,j]:=c[i,j-1];
- b[i,j]:="←"
- end;
- return(c,b);
- end;
由算法LCS_LENGTH计算得到的数组b可用于快速构造序列X=<x1, x2, …, xm>和Y=<y1, y2, …, yn>的最长公共子序列。首先从b[m,n]开始,沿着其中的箭头所指的方向在数组b中搜索。
- 当b[i,j]中遇到"↖"时(意味着xi=yi是LCS的一个元素),表示Xi与Yj的最长公共子序列是由Xi-1与Yj-1的最长公共子序列在尾部加上xi得到的子序列;
- 当b[i,j]中遇到"↑"时,表示Xi与Yj的最长公共子序列和Xi-1与Yj的最长公共子序列相同;
- 当b[i,j]中遇到"←"时,表示Xi与Yj的最长公共子序列和Xi与Yj-1的最长公共子序列相同。
这种方法是按照反序来找LCS的每一个元素的。由于每个数组单元的计算耗费Ο(1)时间,算法LCS_LENGTH耗时Ο(mn)。
2.4、构造最长公共子序列
下面的算法LCS(b,X,i,j)实现根据b的内容打印出Xi与Yj的最长公共子序列。通过算法的调用LCS(b,X,length[X],length[Y]),便可打印出序列X和Y的最长公共子序列。
- Procedure LCS(b,X,i,j);
- begin
- if i=0 or j=0 then return;
- if b[i,j]="↖" then
- begin
- LCS(b,X,i-1,j-1);
- print(x[i]); {打印x[i]}
- end
- else if b[i,j]="↑" then LCS(b,X,i-1,j)
- else LCS(b,X,i,j-1);
- end;
在算法LCS中,每一次的递归调用使i或j减1,因此算法的计算时间为O(m+n)。
例如,设所给的两个序列为X=<A,B,C,B,D,A,B>和Y=<B,D,C,A,B,A>。由算法LCS_LENGTH和LCS计算出的结果如下图所示:
我来说明下此图(参考算法导论)。在序列X={A,B,C,B,D,A,B}和 Y={B,D,C,A,B,A}上,由LCS_LENGTH计算出的表c和b。第i行和第j列中的方块包含了c[i,j]的值以及指向b[i,j]的箭头。在c[7,6]的项4,表的右下角为X和Y的一个LCS<B,C,B,A>的长度。对于i,j>0,项c[i,j]仅依赖于是否有xi=yi,及项c[i-1,j]和c[i,j-1]的值,这几个项都在c[i,j]之前计算。为了重构一个LCS的元素,从右下角开始跟踪b[i,j]的箭头即可,这条路径标示为阴影,这条路径上的每一个“↖”对应于一个使xi=yi为一个LCS的成员的项(高亮标示)。
所以根据上述图所示的结果,程序将最终输出:“B C B A”,或“B D A B”。
可能还是有读者对上面的图看的不是很清楚,下面,我再通过对最大子序列,最长公共子串与最长公共子序列的比较来阐述相关问题@Orisun:
- 最大子序列:最大子序列是要找出由数组成的一维数组中和最大的连续子序列。比如{5,-3,4,2}的最大子序列就是{5,-3,4,2},它的和是8,达到最大;而{5,-6,4,2}的最大子序列是{4,2},它的和是6。你已经看出来了,找最大子序列的方法很简单,只要前i项的和还没有小于0那么子序列就一直向后扩展,否则丢弃之前的子序列开始新的子序列,同时我们要记下各个子序列的和,最后找到和最大的子序列。更多请参看:程序员编程艺术第七章、求连续子数组的最大和。
- 最长公共子串:找两个字符串的最长公共子串,这个子串要求在原字符串中是连续的。其实这又是一个序贯决策问题,可以用动态规划来求解。我们采用一个二维矩阵来记录中间的结果。这个二维矩阵怎么构造呢?直接举个例子吧:"bab"和"caba"(当然我们现在一眼就可以看出来最长公共子串是"ba"或"ab")
b a b
c 0 0 0
a 0 1 0
b 1 0 1
a 0 1 0
我们看矩阵的斜对角线最长的那个就能找出最长公共子串。
不过在二维矩阵上找最长的由1组成的斜对角线也是件麻烦费时的事,下面改进:当要在矩阵是填1时让它等于其左上角元素加1。
b a b
c 0 0 0
a 0 1 0
b 1 0 2
a 0 2 0
这样矩阵中的最大元素就是最长公共子串的长度。
在构造这个二维矩阵的过程中由于得出矩阵的某一行后其上一行就没用了,所以实际上在程序中可以用一维数组来代替这个矩阵。
- 最长公共子序列LCS问题:最长公共子序列与最长公共子串的区别在于最长公共子序列不要求在原字符串中是连续的,比如ADE和ABCDE的最长公共子序列是ADE。
我们用动态规划的方法来思考这个问题如是求解。首先要找到状态转移方程:
等号约定,C1是S1的最右侧字符,C2是S2的最右侧字符,S1‘是从S1中去除C1的部分,S2'是从S2中去除C2的部分。
LCS(S1,S2)等于:
(1)LCS(S1,S2’)
(2)LCS(S1’,S2)
(3)如果C1不等于C2:LCS(S1’,S2’);如果C1等于C2:LCS(S1',S2')+C1;
边界终止条件:如果S1和S2都是空串,则结果也是空串。
下面我们同样要构建一个矩阵来存储动态规划过程中子问题的解。这个矩阵中的每个数字代表了该行和该列之前的LCS的长度。与上面刚刚分析出的状态转移议程相对应,矩阵中每个格子里的数字应该这么填,它等于以下3项的最大值:
(1)上面一个格子里的数字
(2)左边一个格子里的数字
(3)左上角那个格子里的数字(如果C1不等于C2);左上角那个格子里的数字+1(如果C1等于C2)
举个例子:
G C T A
0 0 0 0 0
G 0 1 1 1 1
B 0 1 1 1 1
T 0 1 1 2 2
A 0 1 1 2 3
填写最后一个数字时,它应该是下面三个的最大者:
(1)上边的数字2
(2)左边的数字2
(3)左上角的数字2+1=3,因为此时C1==C2
所以最终结果是3。
在填写过程中我们还是记录下当前单元格的数字来自于哪个单元格,以方便最后我们回溯找出最长公共子串。有时候左上、左、上三者中有多个同时达到最大,那么任取其中之一,但是在整个过程中你必须遵循固定的优先标准。在我的代码中优先级别是左上>左>上。
下图给出了回溯法找出LCS的过程:
2.5、算法的改进
对于一个具体问题,按照一般的算法设计策略设计出的算法,往往在算法的时间和空间需求上还可以改进。这种改进,通常是利用具体问题的一些特殊性。
例如,在算法LCS_LENGTH和LCS中,可进一步将数组b省去。事实上,数组元素c[i,j]的值仅由c[i-1,j-1],c[i-1,j]和c[i,j-1]三个值之一确定,而数组元素b[i,j]也只是用来指示c[i,j]究竟由哪个值确定。因此,在算法LCS中,我们可以不借助于数组b而借助于数组c本身临时判断c[i,j]的值是由c[i-1,j-1],c[i-1,j]和c[i,j-1]中哪一个数值元素所确定,代价是Ο(1)时间。既然b对于算法LCS不是必要的,那么算法LCS_LENGTH便不必保存它。这一来,可节省θ(mn)的空间,而LCS_LENGTH和LCS所需要的时间分别仍然是Ο(mn)和Ο(m+n)。不过,由于数组c仍需要Ο(mn)的空间,因此这里所作的改进,只是在空间复杂性的常数因子上的改进。
另外,如果只需要计算最长公共子序列的长度,则算法的空间需求还可大大减少。事实上,在计算c[i,j]时,只用到数组c的第i行和第i-1行。因此,只要用2行的数组空间就可以计算出最长公共子序列的长度。更进一步的分析还可将空间需求减至min(m, n)。
第三部分、最长公共子序列问题代码
ok,最后给出此面试第56题的代码,参考代码如下,请君自看:
- // LCS.cpp : 定义控制台应用程序的入口点。
- //
- //copyright@zhedahht
- //updated@2011.12.13 July
- #include "stdafx.h"
- #include "string.h"
- #include <iostream>
- using namespace std;
- // directions of LCS generation
- enum decreaseDir {kInit = 0, kLeft, kUp, kLeftUp};
- void LCS_Print(int **LCS_direction,
- char* pStr1, char* pStr2,
- size_t row, size_t col);
- // Get the length of two strings' LCSs, and print one of the LCSs
- // Input: pStr1 - the first string
- // pStr2 - the second string
- // Output: the length of two strings' LCSs
- int LCS(char* pStr1, char* pStr2)
- {
- if(!pStr1 || !pStr2)
- return 0;
- size_t length1 = strlen(pStr1);
- size_t length2 = strlen(pStr2);
- if(!length1 || !length2)
- return 0;
- size_t i, j;
- // initiate the length matrix
- int **LCS_length;
- LCS_length = (int**)(new int[length1]);
- for(i = 0; i < length1; ++ i)
- LCS_length[i] = (int*)new int[length2];
- for(i = 0; i < length1; ++ i)
- for(j = 0; j < length2; ++ j)
- LCS_length[i][j] = 0;
- // initiate the direction matrix
- int **LCS_direction;
- LCS_direction = (int**)(new int[length1]);
- for( i = 0; i < length1; ++ i)
- LCS_direction[i] = (int*)new int[length2];
- for(i = 0; i < length1; ++ i)
- for(j = 0; j < length2; ++ j)
- LCS_direction[i][j] = kInit;
- for(i = 0; i < length1; ++ i)
- {
- for(j = 0; j < length2; ++ j)
- {
- //之前此处的代码有问题,现在订正如下:
- if(i == 0 || j == 0)
- {
- if(pStr1[i] == pStr2[j])
- {
- LCS_length[i][j] = 1;
- LCS_direction[i][j] = kLeftUp;
- }
- else
- {
- if(i > 0)
- {
- LCS_length[i][j] = LCS_length[i - 1][j];
- LCS_direction[i][j] = kUp;
- }
- if(j > 0)
- {
- LCS_length[i][j] = LCS_length[i][j - 1];
- LCS_direction[i][j] = kLeft;
- }
- }
- }
- // a char of LCS is found,
- // it comes from the left up entry in the direction matrix
- else if(pStr1[i] == pStr2[j])
- {
- LCS_length[i][j] = LCS_length[i - 1][j - 1] + 1;
- LCS_direction[i][j] = kLeftUp;
- }
- // it comes from the up entry in the direction matrix
- else if(LCS_length[i - 1][j] > LCS_length[i][j - 1])
- {
- LCS_length[i][j] = LCS_length[i - 1][j];
- LCS_direction[i][j] = kUp;
- }
- // it comes from the left entry in the direction matrix
- else
- {
- LCS_length[i][j] = LCS_length[i][j - 1];
- LCS_direction[i][j] = kLeft;
- }
- }
- }
- LCS_Print(LCS_direction, pStr1, pStr2, length1 - 1, length2 - 1); //调用下面的LCS_Pring 打印出所求子串。
- return LCS_length[length1 - 1][length2 - 1]; //返回长度。
- }
- // Print a LCS for two strings
- // Input: LCS_direction - a 2d matrix which records the direction of
- // LCS generation
- // pStr1 - the first string
- // pStr2 - the second string
- // row - the row index in the matrix LCS_direction
- // col - the column index in the matrix LCS_direction
- void LCS_Print(int **LCS_direction,
- char* pStr1, char* pStr2,
- size_t row, size_t col)
- {
- if(pStr1 == NULL || pStr2 == NULL)
- return;
- size_t length1 = strlen(pStr1);
- size_t length2 = strlen(pStr2);
- if(length1 == 0 || length2 == 0 || !(row < length1 && col < length2))
- return;
- // kLeftUp implies a char in the LCS is found
- if(LCS_direction[row][col] == kLeftUp)
- {
- if(row > 0 && col > 0)
- LCS_Print(LCS_direction, pStr1, pStr2, row - 1, col - 1);
- // print the char
- printf("%c", pStr1[row]);
- }
- else if(LCS_direction[row][col] == kLeft)
- {
- // move to the left entry in the direction matrix
- if(col > 0)
- LCS_Print(LCS_direction, pStr1, pStr2, row, col - 1);
- }
- else if(LCS_direction[row][col] == kUp)
- {
- // move to the up entry in the direction matrix
- if(row > 0)
- LCS_Print(LCS_direction, pStr1, pStr2, row - 1, col);
- }
- }
- int _tmain(int argc, _TCHAR* argv[])
- {
- char* pStr1="abcde";
- char* pStr2="acde";
- LCS(pStr1,pStr2);
- printf("\n");
- system("pause");
- return 0;
- }
程序运行结果如下所示:

扩展:如果题目改成求两个字符串的最长公共子字符串,应该怎么求?子字符串的定义和子串的定义类似,但要求是连续分布在其他字符串中。
比如输入两个字符串BDCABA和ABCBDAB的最长公共字符串有BD和AB,它们的长度都是2。
第四部分、LCS问题的时间复杂度
算法导论上指出,
- 最长公共子序列问题的一个一般的算法、时间复杂度为O(mn)。然后,Masek和Paterson给出了一个O(mn/lgn)时间内执行的算法,其中n<=m,而且此序列是从一个有限集合中而来。在输入序列中没有出现超过一次的特殊情况中,Szymansk说明这个问题可在O((n+m)lg(n+m))内解决。
- 一篇由Gilbert和Moore撰写的关于可变长度二元编码的早期论文中有这样的应用:在所有的概率pi都是0的情况下构造最优二叉查找树,这篇论文给出一个O(n^3)时间的算法。Hu和Tucker设计了一个算法,它在所有的概率pi都是0的情况下,使用O(n)的时间和O(n)的空间,最后,Knuth把时间降到了O(nlgn)。
关于此动态规划算法更多可参考 算法导论一书第15章 动态规划问题,至于关于此面试第56题的更多,可参考我即将整理上传的答案V04版第41-60题的答案。
补充:一网友提供的关于此最长公共子序列问题的java算法源码,我自行测试了下,正确:
import java.util.Random;
public class LCS{
public static void main(String[] args){
//设置字符串长度
int substringLength1 = 20;
int substringLength2 = 20; //具体大小可自行设置
// 随机生成字符串
String x = GetRandomStrings(substringLength1);
String y = GetRandomStrings(substringLength2);
Long startTime = System.nanoTime();
// 构造二维数组记录子问题x[i]和y[i]的LCS的长度
int[][] opt = new int[substringLength1 + 1][substringLength2 + 1];
// 动态规划计算所有子问题
for (int i = substringLength1 - 1; i >= 0; i--){
for (int j = substringLength2 - 1; j >= 0; j--){
if (x.charAt(i) == y.charAt(j))
opt[i][j] = opt[i + 1][j + 1] + 1; //参考上文我给的公式。
else
opt[i][j] = Math.max(opt[i + 1][j], opt[i][j + 1]); //参考上文我给的公式。
}
}
-------------------------------------------------------------------------------------
理解上段,参考上文我给的公式:
根据上述结论,可得到以下公式,
如果我们记字符串Xi和Yj的LCS的长度为c[i,j],我们可以递归地求c[i,j]: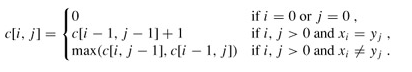
-------------------------------------------------------------------------------------
System.out.println("substring1:"+x);
System.out.println("substring2:"+y);
System.out.print("LCS:");
int i = 0, j = 0;
while (i < substringLength1 && j < substringLength2){
if (x.charAt(i) == y.charAt(j)){
System.out.print(x.charAt(i));
i++;
j++;
} else if (opt[i + 1][j] >= opt[i][j + 1])
i++;
else
j++;
}
Long endTime = System.nanoTime();
System.out.println(" Totle time is " + (endTime - startTime) + " ns");
}
//取得定长随机字符串
public static String GetRandomStrings(int length){
StringBuffer buffer = new StringBuffer("abcdefghijklmnopqrstuvwxyz");
StringBuffer sb = new StringBuffer();
Random r = new Random();
int range = buffer.length();
for (int i = 0; i < length; i++){
sb.append(buffer.charAt(r.nextInt(range)));
}
return sb.toString();
}
}
eclipse运行结果为:
substring1:akqrshrengxqiyxuloqk
substring2:tdzbujtlqhecaqgwfzbc
LCS:qheq Totle time is 818058 ns
经典算法研究系列:四、教你通透彻底理解:BFS和DFS优先搜索算法
4、教你通透彻底理解:BFS和DFS优先搜索算法
作者:July 二零一一年一月一日
---------------------------------
本人参考:算法导论
本人声明:个人原创,转载请注明出处。
ok,开始。
翻遍网上,关于此类BFS和DFS算法的文章,很多。但,都说不出个所以然来。
读完此文,我想,
你对图的广度优先搜索和深度优先搜索定会有个通通透透,彻彻底底的认识。
---------------------
咱们由BFS开始:
首先,看下算法导论一书关于 此BFS 广度优先搜索算法的概述。
算法导论第二版,中译本,第324页。
广度优先搜索(BFS)
在Prime最小生成树算法,和Dijkstra单源最短路径算法中,都采用了与BFS 算法类似的思想。
BFS(G, s)
1 for each vertex u ∈ V [G] - {s}
2 do color[u] ← WHITE
3 d[u] ← ∞
4 π[u] ← NIL
//除了源顶点s之外,第1-4行置每个顶点为白色,置每个顶点u的d[u]为无穷大,
//置每个顶点的父母为NIL。
5 color[s] ← GRAY
//第5行,将源顶点s置为灰色,这是因为在过程开始时,源顶点已被发现。
6 d[s] ← 0 //将d[s]初始化为0。
7 π[s] ← NIL //将源顶点的父顶点置为NIL。
8 Q ← Ø
9 ENQUEUE(Q, s) //入队
//第8、9行,初始化队列Q,使其仅含源顶点s。
10 while Q ≠ Ø
11 do u ← DEQUEUE(Q) //出队
//第11行,确定队列头部Q头部的灰色顶点u,并将其从Q中去掉。
12 for each v ∈ Adj[u] //for循环考察u的邻接表中的每个顶点v
13 do if color[v] = WHITE
14 then color[v] ← GRAY //置为灰色
15 d[v] ← d[u] + 1 //距离被置为d[u]+1
16 π[v] ← u //u记为该顶点的父母
17 ENQUEUE(Q, v) //插入队列中
18 color[u] ← BLACK //u 置为黑色
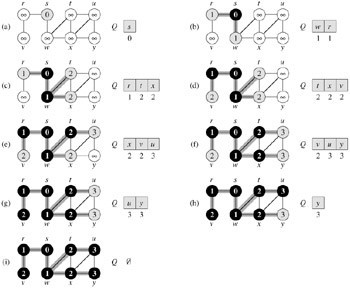
由下图及链接的演示过程,清晰在目,也就不用多说了:

ok,不再赘述。接下来,具体讲解深度优先搜索算法。
深度优先探索算法 DFS
//u 为 v 的先辈或父母。
DFS(G)
1 for each vertex u ∈ V [G]
2 do color[u] ← WHITE
3 π[u] ← NIL
//第1-3行,把所有顶点置为白色,所有π 域被初始化为NIL。
4 time ← 0 //复位时间计数器
5 for each vertex u ∈ V [G]
6 do if color[u] = WHITE
7 then DFS-VISIT(u) //调用DFS-VISIT访问u,u成为深度优先森林中一棵新的树
//第5-7行,依次检索V中的顶点,发现白色顶点时,调用DFS-VISIT访问该顶点。
//每个顶点u 都对应于一个发现时刻d[u]和一个完成时刻f[u]。
DFS-VISIT(u)
1 color[u] ← GRAY //u 开始时被发现,置为白色
2 time ← time +1 //time 递增
3 d[u] <-time //记录u被发现的时间
4 for each v ∈ Adj[u] //检查并访问 u 的每一个邻接点 v
5 do if color[v] = WHITE //如果v 为白色,则递归访问v。
6 then π[v] ← u //置u为 v的先辈
7 DFS-VISIT(v) //递归深度,访问邻结点v
8 color[u] <-BLACK //u 置为黑色,表示u及其邻接点都已访问完成
9 f [u] ▹ time ← time +1 //访问完成时间记录在f[u]中。
对于每个顶点v(-V,过程DFS-VISIT仅被调用依次,因为只有对白色顶点才会调用此过程。
第4-7行,执行时间为O(E)。
因此,总的执行时间为O(V+E)。
下面的链接,给出了深度优先搜索的演示系统:
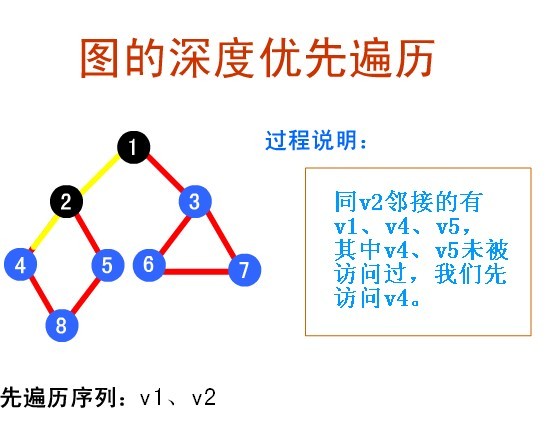
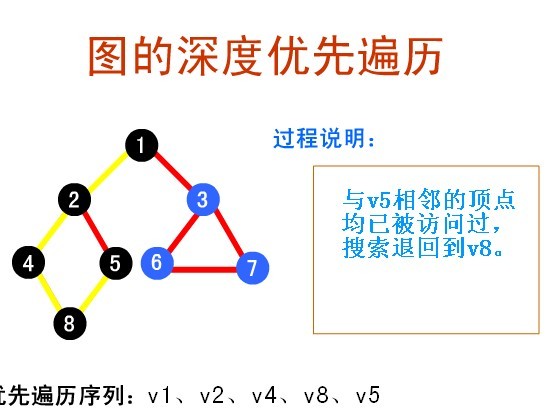
图的深度优先遍历演示系统:
http://sjjg.js.zwu.edu.cn/SFXX/sf1/sdyxbl.html
===============
最后,咱们再来看深度优先搜索的递归实现与非递归实现
1、DFS 递归实现:
void dftR(PGraphMatrix inGraph)
{
PVexType v;
assertF(inGraph!=NULL,"in dftR, pass in inGraph is null/n");
printf("/n===start of dft recursive version===/n");
for(v=firstVertex(inGraph);v!=NULL;v=nextVertex(inGraph,v))
if(v->marked==0)
dfsR(inGraph,v);
printf("/n===end of dft recursive version===/n");
}
void dfsR(PGraphMatrix inGraph,PVexType inV)
{
PVexType v1;
assertF(inGraph!=NULL,"in dfsR,inGraph is null/n");
assertF(inV!=NULL,"in dfsR,inV is null/n");
inV->marked=1;
visit(inV);
for(v1=firstAdjacent(inGraph,inV);v1!=NULL;v1=nextAdjacent(inGraph,inV,v1))
//v1当为v的邻接点。
if(v1->marked==0)
dfsR(inGraph,v1);
}
2、DFS 非递归实现
非递归版本---借助结点类型为队列的栈实现
联系树的前序遍历的非递归实现:
可知,其中无非是分成“探左”和“访右”两大块访右需借助栈中弹出的结点进行.
在图的深度优先搜索中,同样可分成“深度探索”和“回访上层未访结点”两块:
1、图的深度探索这样一个过程和树的“探左”完全一致,
只要对已访问过的结点作一个判定即可。
2、而图的回访上层未访结点和树的前序遍历中的“访右”也是一致的.
但是,对于树而言,是提供rightSibling这样的操作的,因而访右相当好实现。
在这里,若要实现相应的功能,考虑将每一个当前结点的下层结点中,如果有m个未访问结点,
则最左的一个需要访问,而将剩余的m-1个结点按从左到右的顺序推入一个队列中。
并将这个队列压入一个堆栈中。
这样,当当前的结点的邻接点均已访问或无邻接点需要回访时,
则从栈顶的队列结点中弹出队列元素,将队列中的结点元素依次出队,
若已访问,则继续出队(当当前队列结点已空时,则继续出栈,弹出下一个栈顶的队列),
直至遇到有未访问结点(访问并置当前点为该点)或直到栈为空(则当前的深度优先搜索树停止搜索)。
将算法通过精简过的C源程序的方式描述如下:
//dfsUR:功能从一个树的某个结点inV发,以深度优先的原则访问所有与它相邻的结点
void dfsUR(PGraphMatrix inGraph,PVexType inV)
{
PSingleRearSeqQueue tmpQ; //定义临时队列,用以接受栈顶队列及压栈时使用
PSeqStack testStack; //存放当前层中的m-1个未访问结点构成队列的堆栈.
//一些变量声明,初始化动作
//访问当前结点
inV->marked=1; //当marked值为1时将不必再访问。
visit(inV);
do
{
flag2=0;
//flag2是一个重要的标志变量,用以、说明当前结点的所有未访问结点的个数,两个以上的用2代表
//flag2:0:current node has no adjacent which has not been visited.
//1:current node has only one adjacent node which has not been visited.
//2:current node has more than one adjacent node which have not been visited.
v1=firstAdjacent(inGraph,inV); //邻接点v1
while(v1!=NULL) //访问当前结点的所有邻接点
{
if(v1->marked==0) //..
{
if(flag2==0) //当前结点的邻接点有0个未访问
{
//首先,访问最左结点
visit(v1);
v1->marked=1; //访问完成
flag2=1; //
//记录最左儿子
lChildV=v1;
//save the current node's first unvisited(has been visited at this time)adjacent node
}
else if(flag2==1) //当前结点的邻接点有1个未访问
{
//新建一个队列,申请空间,并加入第一个结点
flag2=2;
}
else if(flag2==2)//当前结点的邻接点有2个未被访问
{
enQueue(tmpQ,v1);
}
}
v1=nextAdjacent(inGraph,inV,v1);
}
if(flag2==2)//push adjacent nodes which are not visited.
{
//将存有当前结点的m-1个未访问邻接点的队列压栈
seqPush(testStack,tmpQ);
inV=lChildV;
}
else if(flag2==1)//only has one adjacent which has been visited.
{
//只有一个最左儿子,则置当前点为最左儿子
inV=lChildV;
}
else if(flag2==0)
//has no adjacent nodes or all adjacent nodes has been visited
{
//当当前的结点的邻接点均已访问或无邻接点需要回访时,则从栈顶的队列结点中弹出队列元素,
//将队列中的结点元素依次出队,若已访问,则继续出队(当当前队列结点已空时,
//则继续出栈,弹出下一个栈顶的队列),直至遇到有未访问结点(访问并置当前点为该点)或直到栈为空。
flag=0;
while(!isNullSeqStack(testStack)&&!flag)
{
v1=frontQueueInSt(testStack); //返回栈顶结点的队列中的队首元素
deQueueInSt(testStack); //将栈顶结点的队列中的队首元素弹出
if(v1->marked==0)
{
visit(v1);
v1->marked=1;
inV=v1;
flag=1;
}
}
}
}while(!isNullSeqStack(testStack));//the algorithm ends when the stack is null
}
-----------------------------
上述程序的几点说明:
所以,这里应使用的数据结构的构成方式应该采用下面这种形式:
1)队列的实现中,每个队列结点均为图中的结点指针类型.
定义一个以队列尾部下标加队列长度的环形队列如下:
struct SingleRearSeqQueue;
typedef PVexType QElemType;
typedef struct SingleRearSeqQueue* PSingleRearSeqQueue;
struct SingleRearSeqQueue
{
int rear;
int quelen;
QElemType dataPool[MAXNUM];
};
其余基本操作不再赘述.
2)堆栈的实现中,每个堆栈中的结点元素均为一个指向队列的指针,定义如下:
#define SEQ_STACK_LEN 1000
#define StackElemType PSingleRearSeqQueue
struct SeqStack;
typedef struct SeqStack* PSeqStack;
struct SeqStack
{
StackElemType dataArea[SEQ_STACK_LEN];
int slot;
};
为了提供更好的封装性,对这个堆栈实现两种特殊的操作
2.1) deQueueInSt操作用于将栈顶结点的队列中的队首元素弹出.
void deQueueInSt(PSeqStack inStack)
{
if(isEmptyQueue(seqTop(inStack))||isNullSeqStack(inStack))
{
printf("in deQueueInSt,under flow!/n");
return;
}
deQueue(seqTop(inStack));
if(isEmptyQueue(seqTop(inStack)))
inStack->slot--;
}
2.2) frontQueueInSt操作用以返回栈顶结点的队列中的队首元素.
QElemType frontQueueInSt(PSeqStack inStack)
{
if(isEmptyQueue(seqTop(inStack))||isNullSeqStack(inStack))
{
printf("in frontQueueInSt,under flow!/n");
return '/r';
}
return getHeadData(seqTop(inStack));
}
===================
ok,本文完。
经典算法研究系列:六、教你初步了解KMP算法、updated
教你初步了解KMP算法
作者: July 、saturnma、上善若水。 时间; 二零一一年一月一日
-----------------------
本文参考:数据结构(c语言版) 李云清等编著、算法导论
引言:
在文本编辑中,我们经常要在一段文本中某个特定的位置找出 某个特定的字符或模式。
由此,便产生了字符串的匹配问题。
本文由简单的字符串匹配算法开始,再到KMP算法,由浅入深,教你从头到尾彻底理解KMP算法。
来看算法导论一书上关于此字符串问题的定义:
假设文本是一个长度为n的数组T[1...n],模式是一个长度为m<=n的数组P[1....m]。
进一步假设P和T的元素都是属于有限字母表Σ.中的字符。
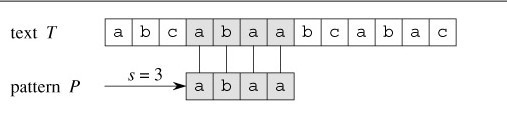
依据上图,再来解释下字符串匹配问题。目标是找出所有在文本T=abcabaabcaabac中的模式P=abaa所有出现。
该模式仅在文本中出现了一次,在位移s=3处。位移s=3是有效位移。
第一节、简单的字符串匹配算法
简单的字符串匹配算法用一个循环来找出所有有效位移,
该循环对n-m+1个可能的每一个s值检查条件P[1....m]=T[s+1....s+m]。
NAIVE-STRING-MATCHER(T, P)
1 n ← length[T]
2 m ← length[P]
3 for s ← 0 to n - m
4 do if P[1 ‥ m] = T[s + 1 ‥ s + m]
//对n-m+1个可能的位移s中的每一个值,比较相应的字符的循环必须执行m次。
5 then print "Pattern occurs with shift" s

简单字符串匹配算法,上图针对文本T=acaabc 和模式P=aab。
上述第4行代码,n-m+1个可能的位移s中的每一个值,比较相应的字符的循环必须执行m次。
所以,在最坏情况下,此简单模式匹配算法的运行时间为O((n-m+1)m)。
--------------------------------
下面我再来举个具体例子,并给出一具体运行程序:
对于目的字串target是banananobano,要匹配的字串pattern是nano,的情况,
下面是匹配过程,原理很简单,只要先和target字串的第一个字符比较,
如果相同就比较下一个,如果不同就把pattern右移一下,
之后再从pattern的每一个字符比较,这个算法的运行过程如下图。
//index表示的每n次匹配的情形。

#include<iostream>
#include<string>
using namespace std;
int match(const string& target,const string& pattern)
{
int target_length = target.size();
int pattern_length = pattern.size();
int target_index = 0;
int pattern_index = 0;
while(target_index < target_length && pattern_index < pattern_length)
{
if(target[target_index]==pattern[pattern_index])
{
++target_index;
++pattern_index;
}
else
{
target_index -= (pattern_index-1);
pattern_index = 0;
}
}
if(pattern_index == pattern_length)
{
return target_index - pattern_length;
}
else
{
return -1;
}
}
int main()
{
cout<<match("banananobano","nano")<<endl;
return 0;
}
//运行结果为4。
上面的算法进间复杂度是O(pattern_length*target_length),
我们主要把时间浪费在什么地方呢,
观查index =2那一步,我们已经匹配了3个字符,而第4个字符是不匹配的,这时我们已经匹配的字符序列是nan,
此时如果向右移动一位,那么nan最先匹配的字符序列将是an,这肯定是不能匹配的,
之后再右移一位,匹配的是nan最先匹配的序列是n,这是可以匹配的。
如果我们事先知道pattern本身的这些信息就不用每次匹配失败后都把target_index回退回去,
这种回退就浪费了很多不必要的时间,如果能事先计算出pattern本身的这些性质,
那么就可以在失配时直接把pattern移动到下一个可能的位置,
把其中根本不可能匹配的过程省略掉,
如上表所示我们在index=2时失配,此时就可以直接把pattern移动到index=4的状态,
kmp算法就是从此出发。
第二节、KMP算法
2.1、 覆盖函数(overlay_function)
覆盖函数所表征的是pattern本身的性质,可以让为其表征的是pattern从左开始的所有连续子串的自我覆盖程度。
比如如下的字串,abaabcaba
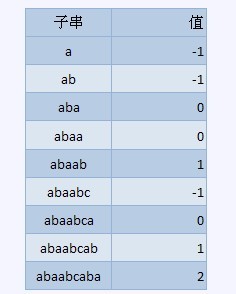
由于计数是从0始的,因此覆盖函数的值为0说明有1个匹配,对于从0还是从来开始计数是偏好问题,
具体请自行调整,其中-1表示没有覆盖,那么何为覆盖呢,下面比较数学的来看一下定义,比如对于序列
a0a1...aj-1 aj
要找到一个k,使它满足
a0a1...ak-1ak=aj-kaj-k+1...aj-1aj
而没有更大的k满足这个条件,就是说要找到尽可能大k,使pattern前k字符与后k字符相匹配,k要尽可能的大,
原因是如果有比较大的k存在,而我们选择较小的满足条件的k,
那么当失配时,我们就会使pattern向右移动的位置变大,而较少的移动位置是存在匹配的,这样我们就会把可能匹配的结果丢失。
比如下面的序列,
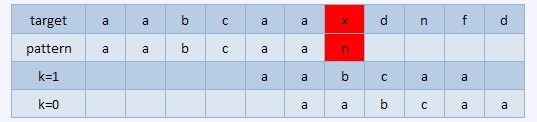
在红色部分失配,正确的结果是k=1的情况,把pattern右移4位,如果选择k=0,右移5位则会产生错误。
计算这个overlay函数的方法可以采用递推,可以想象如果对于pattern的前j个字符,如果覆盖函数值为k
a0a1...ak-1ak=aj-kaj-k+1...aj-1aj
则对于pattern的前j+1序列字符,则有如下可能
⑴ pattern[k+1]==pattern[j+1] 此时overlay(j+1)=k+1=overlay(j)+1
⑵ pattern[k+1]≠pattern[j+1] 此时只能在pattern前k+1个子符组所的子串中找到相应的overlay函数,h=overlay(k),如果此时pattern[h+1]==pattern[j+1],则overlay(j+1)=h+1否则重复(2)过程.
下面给出一段计算覆盖函数的代码:
#include<iostream>
#include<string>
using namespace std;
void compute_overlay(const string& pattern)
{
const int pattern_length = pattern.size();
int *overlay_function = new int[pattern_length];
int index;
overlay_function[0] = -1;
for(int i=1;i<pattern_length;++i)
{
index = overlay_function[i-1];
//store previous fail position k to index;
while(index>=0 && pattern[i]!=pattern[index+1])
{
index = overlay_function[index];
}
if(pattern[i]==pattern[index+1])
{
overlay_function[i] = index + 1;
}
else
{
overlay_function[i] = -1;
}
}
for(i=0;i<pattern_length;++i)
{
cout<<overlay_function[i]<<endl;
}
delete[] overlay_function;
}
int main()
{
string pattern = "abaabcaba";
compute_overlay(pattern);
return 0;
}
运行结果为:
-1
-1
0
0
1
-1
0
1
2
Press any key to continue
-------------------------------------
2.2、kmp算法
有了覆盖函数,那么实现kmp算法就是很简单的了,我们的原则还是从左向右匹配,但是当失配发生时,我们不用把target_index向回移动,target_index前面已经匹配过的部分在pattern自身就能体现出来,只要动pattern_index就可以了。
当发生在j长度失配时,只要把pattern向右移动j-overlay(j)长度就可以了。
如果失配时pattern_index==0,相当于pattern第一个字符就不匹配,
这时就应该把target_index加1,向右移动1位就可以了。
ok,下图就是KMP算法的过程(红色即是采用KMP算法的执行过程):
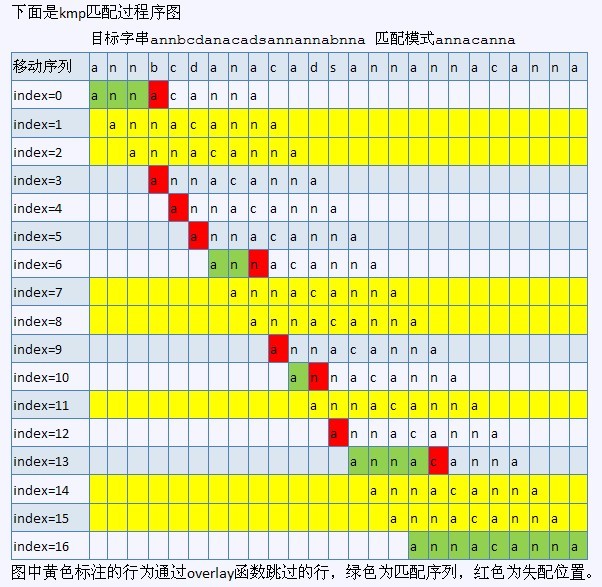
另一作者saturnman发现,在上述KMP匹配过程图中,index=8和index=11处画错了。还有,anaven也早已发现,index=3处也画错了。非常感谢。但图已无法修改,见谅。
KMP 算法可在O(n+m)时间内完成全部的串的模式匹配工作。
ok,最后给出KMP算法实现的c++代码:
#include<iostream>
#include<string>
#include<vector>
using namespace std;
int kmp_find(const string& target,const string& pattern)
{
const int target_length = target.size();
const int pattern_length = pattern.size();
int * overlay_value = new int[pattern_length];
overlay_value[0] = -1;
int index = 0;
for(int i=1;i<pattern_length;++i)
{
index = overlay_value[i-1];
while(index>=0 && pattern[index+1]!=pattern[i])
{
index = overlay_value[index];
}
if(pattern[index+1]==pattern[i])
{
overlay_value[i] = index +1;
}
else
{
overlay_value[i] = -1;
}
}
//match algorithm start
int pattern_index = 0;
int target_index = 0;
while(pattern_index<pattern_length&&target_index<target_length)
{
if(target[target_index]==pattern[pattern_index])
{
++target_index;
++pattern_index;
}
else if(pattern_index==0)
{
++target_index;
}
else
{
pattern_index = overlay_value[pattern_index-1]+1;
}
}
if(pattern_index==pattern_length)
{
return target_index-pattern_index;
}
else
{
return -1;
}
delete [] overlay_value;
}
int main()
{
string source = " annbcdanacadsannannabnna";
string pattern = " annacanna";
cout<<kmp_find(source,pattern)<<endl;
return 0;
}
//运行结果为 -1.
第三节、kmp算法的来源
kmp如此精巧,那么它是怎么来的呢,为什么要三个人合力才能想出来。其实就算没有kmp算法,人们在字符匹配中也能找到相同高效的算法。这种算法,最终相当于kmp算法,只是这种算法的出发点不是覆盖函数,不是直接从匹配的内在原理出发,而使用此方法的计算的覆盖函数过程序复杂且不易被理解,但是一但找到这个覆盖函数,那以后使用同一pattern匹配时的效率就和kmp一样了,其实这种算法找到的函数不应叫做覆盖函数,因为在寻找过程中根本没有考虑是否覆盖的问题。
说了这么半天那么这种方法是什么呢,这种方法是就大名鼎鼎的确定的有限自动机(Deterministic finite state automaton DFA),DFA可识别的文法是3型文法,又叫正规文法或是正则文法,既然可以识别正则文法,那么识别确定的字串肯定不是问题(确定字串是正则式的一个子集)。对于如何构造DFA,是有一个完整的算法,这里不做介绍了。在识别确定的字串时使用DFA实在是大材小用,DFA可以识别更加通用的正则表达式,而用通用的构建DFA的方法来识别确定的字串,那这个overhead就显得太大了。
kmp算法的可贵之处是从字符匹配的问题本身特点出发,巧妙使用覆盖函数这一表征pattern自身特点的这一概念来快速直接生成识别字串的DFA,因此对于kmp这种算法,理解这种算法高中数学就可以了,但是如果想从无到有设计出这种算法是要求有比较深的数学功底的。
第四节、精确字符匹配的常见算法的解析
KMP算法:
KMP就是串匹配算法
运用自动机原理
比如说
我们在S中找P
设P={ababbaaba}
我们将P对自己匹配
下面是求的过程:{依次记下匹配失败的那一位}
[2]ababbaaba
.......ababbaaba[1]
[3]ababbaaba
.........ababbaaba[1]
[4]ababbaaba
.........ababbaaba[2]
[5]ababbaaba
.........ababbaaba[3]
[6]ababbaaba
................ababbaaba[1]
[7]ababbaaba
................ababbaaba[2]
[8]ababbaaba
..................ababbaaba[2]
[9]ababbaaba
..................ababbaaba[3]
得到Next数组『0,1,1,2,3,1,2,2,3』
主过程:
[1]i:=1 j:=1
[2]若(j>m)或(i>n)转[4]否则转[3]
[3]若j=0或a[i]=b[j]则【inc(i)inc(j)转[2]】否则【j:=next[j]转2】
[4]若j>m则return(i-m)否则return -1;
若返回-1表示失败,否则表示在i-m处成功
BM算法也是一种快速串匹配算法,KMP算法的主要区别是匹配操作的方向不同。虽然T右移的计算方法却发生了较大的变化。
为方便讨论,T="dist :c->{dist称为滑动距离函数,它给出了正文中可能出现的任意字符在模式中的位置。函数 m – j j为 dist(m+1 若c = tm
例如,pattern",则p)a)t)dist(= 2,r)n)BM算法的基本思想是:假设将主串中自位置i + dist(si)位置开始重新进行新一轮的匹配,其效果相当于把模式和主串向右滑过一段距离si),即跳过si)个字符而无需进行比较。
下面是一个S ="T="BM算法可以大大加快串匹配的速度。
下面是KMP算法部分,把调用BM函数便可。
- #include <iostream>
- using namespace std;
- int Dist(char *t,char ch)
- {
- int len = strlen(t);
- int i = len - 1;
- if(ch == t[i])
- return len;
- i--;
- while(i >= 0)
- {
- if(ch == t[i])
- return len - 1 - i;
- else
- i--;
- }
- return len;
- }
- int BM(char *s,char *t)
- {
- int n = strlen(s);
- int m = strlen(t);
- int i = m-1;
- int j = m-1;
- while(j>=0 && i<n)
- {
- if(s[i] == t[j])
- {
- i--;
- j--;
- }
- else
- {
- i += Dist(t,s[i]);
- j = m-1;
- }
- }
- if(j < 0)
- {
- return i+1;
- }
- return -1;
- }
Horspool算法
这个算法是由R.Nigel Horspool在1980年提出的。其滑动思想非常简单,就是从后往前匹配模式串,若在某一位失去匹配,此位对应的文本串字符为c,那就将模式串向右滑动,使模式
串之前最近的c对准这一位,再从新从后往前检查。那如果之前找不到c怎么办?那好极了,直接将整个模式串滑过这一位。
例如:文本串:abdabaca
模式串:baca倒数第2位失去匹配,模式串之前又没有d,那模式串就可以整个滑过,变成这样:
文本串:abdabaca
模式串: baca发现倒数第1位就失去匹配,之前1位有c,那就向右滑动1位:
文本串:abdabaca
模式串: baca实现代码:
- #include <iostream>
- #include <vector>
- #include <string>
- #include <cstdlib>
- using namespace std;
- int Horspool_match(const string & S,const string & M,int pos)
- {
- int S_len = S.size();
- int M_len = M.size();
- int Mi = M_len-1,Si= pos+Mi; //这里的串的第1个元素下标是0
- if( (S_len-pos) < M_len )
- return -1;
- while ( (Mi>-1) && (Si<S_len) )
- {
- if (S[Si] == M[Mi])
- {
- --Mi;
- --Si;
- }
- else
- {
- do
- {
- Mi--;
- }
- while( (S[Si]!=M[Mi]) || (Mi>-1) );
- Mi = M_len - 1;
- Si += M_len - 1;
- }
- }
- if(Si < S_len)
- return(Si + 1);
- else
- return -1;
- }
- int main( )
- {
- string S="abcdefghabcdefghhiijiklmabc";
- string T="hhiij";
- int pos = Horspool_match(S,T,3);
- cout<<"/n"<<pos<<endl;
- system("pause");
- return 0;
- }
SUNDAY算法:
BM算法的改进的算法SUNDAY--Boyer-Moore-Horspool-Sunday Aglorithm
BM算法优于KMP
SUNDAY 算法描述:
字符串查找算法中,最著名的两个是KMP算法(Knuth-Morris-Pratt)和BM算法(Boyer-Moore)。两个算法在最坏情况下均具有线性的查找时间。但是在实用上,KMP算法并不比最简单的c库函数strstr()快多少,而BM算法则往往比KMP算法快上3-5倍。但是BM算法还不是最快的算法,这里介绍一种比BM算法更快一些的查找算法即Sunday算法。
例如我们要在"substring searching algorithm"查找"search",刚开始时,把子串与文本左边对齐:
substring searching algorithm
search
^
结果在第二个字符处发现不匹配,于是要把子串往后移动。但是该移动多少呢?这就是各种算法各显神通的地方了,最简单的做法是移动一个字符位置;KMP是利用已经匹配部分的信息来移动;BM算法是做反向比较,并根据已经匹配的部分来确定移动量。这里要介绍的方法是看紧跟在当前子串之后的那个字符(上图中的 'i')。
显然,不管移动多少,这个字符是肯定要参加下一步的比较的,也就是说,如果下一步匹配到了,这个字符必须在子串内。所以,可以移动子串,使子串中的最右边的这个字符与它对齐。现在子串'search'中并不存在'i',则说明可以直接跳过一大片,从'i'之后的那个字符开始作下一步的比较,如下图:
substring searching algorithm
search
^
比较的结果,第一个字符就不匹配,再看子串后面的那个字符,是'r',它在子串中出现在倒数第三位,于是把子串向前移动三位,使两个'r'对齐,如下:
substring searching algorithm
search
^
哈!这次匹配成功了!回顾整个过程,我们只移动了两次子串就找到了匹配位置,可以证明,用这个算法,每一步的移动量都比BM算法要大,所以肯定比BM算法更快。
- #include<iostream>
- #include<fstream>
- #include<vector>
- #include<algorithm>
- #include<string>
- #include<list>
- #include<functional>
- using namespace std;
- int main()
- {
- char *text=new char[100];
- text="substring searching algorithm search";
- char *patt=new char[10];
- patt="search";
- size_t temp[256];
- size_t *shift=temp;
- size_t patt_size=strlen(patt);
- cout<<"size : "<<patt_size<<endl;
- for(size_t i=0;i<256;i++)
- *(shift+i)=patt_size+1;//所有值赋于7,对这题而言
- for(i=0;i<patt_size;i++)
- *(shift+unsigned char(*(patt+i) ) )=patt_size-i;
- /* // 移动3步-->shift['r']=6-3=3;移动三步
- //shift['s']=6步,shitf['e']=5以此类推
- */
- size_t text_size=strlen(text);
- size_t limit=text_size-i+1;
- for(i=0;i<limit;i+=shift[text[i+patt_size] ] )
- if(text[i]==*patt)
- {
- /* ^13--这个r是位,从0开始算
- substring searching algorithm
- search
- searching-->这个s为第10位,从0开始算
- 如果第一个字节匹配,那么继续匹配剩下的
- */
- char* match_text=text+i+1;
- size_t match_size=1;
- do{
- if(match_size==patt_size)
- cout<<"the no is "<<i<<endl;
- }while( (*match_text++)==patt[match_size++] );
- }
- cout<<endl;
- }
- delete []text;
- delete []patt;
- return 0;
- }
- //运行结果如下:
- /*
- size : 6
- the no is 10
- the no is 30
- Press any key to continue
- */
微软面试100题系列:一道合并链表问题的解答[第42题]
微软面试100题V0.1版第42题 合并链表解答
July、网友 二零一一年一月2日
------------------------------------
本文参考:本人整理的微软面试100题系列V0.1版第42题、网友的回复。
本人声明:本人对此微软等100题系列任何资料享有版权。
由于微软等面试100题系列的答案V0.2版,答案V0.3版[第1-40题答案]都已经放出,
而答案V0.3版最近新整理好,在上传之前,选择性的贴几道题的答案,以让读者检验。
至于第1-40题的答案,日后,我也会不定期的选择性的在我博客里一一阐述。
ok,第56题[最长公共子序列]的答案,已在我的博文:
24个经典算法系列:3、动态规划算法解微软面试第56题 中明确阐述了。
这次,咱们来看一道链表合并的面试题。
42、请修改append函数,利用这个函数实现:两个非降序链表的并集,
1->2->3 和 2->3->5 并为 1->2->3->5另外只能输出结果,不能修改两个链表的数据。
此题,合并链表,要求将俩个非有序排列的链表,有顺序的合并。如下:
//程序一、引自一网友。
#include <stdio.h>
#include <malloc.h>
typedef struct lnode {
int data;
struct lnode *next;
}lnode,*linklist;
linklist creatlist(int m)//创建链表
{
linklist p,l,s;
int i;
p=l=(linklist)malloc(sizeof(lnode));
p->next=NULL;
printf("请输入链表中的一个数字:");
scanf("%d",&p->data);
for(i=2;i<=m;i++)
{
s=(linklist)malloc(sizeof(lnode));
s->next = NULL;
printf("请输入第%d个数字",i);
scanf("%d",&s->data);
p->next=s;
p=p->next;
}
printf("/n");
return l;
}
void print(linklist h)//打印链表
{
linklist p=h->next;
int t=1;
printf("打印各个数字:/n");
do
{
printf("请输出第%d个数:",t);
printf("%d/n",p->data);
p=p->next;
t++;
}while(p);
}
linklist mergelist(void)//两个链表合并
{
int e,n;
linklist pa,pb,pc,head;
printf("请输入第一个链表的长度:");
scanf("%d",&e);
pa=creatlist(e);
printf("请输入第二个链表的长度:");
scanf("%d",&n);
pb=creatlist(n);
head=pc=(linklist)malloc(sizeof(lnode));
pc->next=NULL;
while(pa&&pb)
{
if(pa->data<=pb->data)
{
pc->next=pa;
pc=pa;
pa=pa->next;
}
else
{
pc->next=pb;
pc=pb;
pb=pb->next;
}
}
pc->next=pa?pa:pb;
return head;
}
void main()
{
linklist head;
head=mergelist();
print(head);
}
///
请输入第一个链表的长度:5
请输入链表中的一个数字:3
请输入第2个数字2
请输入第3个数字1
请输入第4个数字7
请输入第5个数字9
请输入第二个链表的长度:5
请输入链表中的一个数字:6
请输入第2个数字4
请输入第3个数字5
请输入第4个数字8
请输入第5个数字7
打印各个数字:
请输出第1个数:3
请输出第2个数:2
请输出第3个数:1
请输出第4个数:6
请输出第5个数:4
请输出第6个数:5
请输出第7个数:7
请输出第8个数:8
请输出第9个数:7
请输出第10个数:9
Press any key to continue
//程序二、引用yangsen600。
#include <stdio.h>
#include <stdlib.h>
#include <malloc.h>
struct Node
{
int num;
Node * next;
};
Node * createTail()
{
int x;
Node *head = NULL, *p = NULL, *tail = NULL;
puts("/nplease enter some digits(end of '.'):");
while( 1 == scanf("%d",&x) )
{
p = (Node *)malloc(sizeof(Node));
p->num = x;
p->next = NULL;
if( NULL == head )
{
tail = p;
head = tail;
}
else
{
tail->next = p;
tail = p;
}
}
getchar();
return head;
}
Node * CombinationNode(Node* head1, Node* head2)
{
Node *head,*tail,*p = head1,*q = head2,*s;
if( NULL == p )
return q;
if( NULL == q )
return p;
tail = p;
if( p->num > q->num)
tail = q;
head = tail;
while( NULL != p && NULL != q )
{
if(p->num <= q->num )
//如果p所指元素<q所指元素,那么把p所指元素,率先拉入合并后的链表中,
//p赋给s,并从p的下一个元素p->next查找。
//直到发现p所指 不再 < q,而是p > q了 即转至下述代码的else部分。
{
s = p;
p = p->next;
}
else
{
s = q;
q = q->next;
}
tail->next = s;
tail = s;
}
if( NULL == p )
p = q;
s = p;
tail->next = s;
return head;
}
void printHead(Node *head)
{
if( NULL == head )
return;
printf("List: ");
while(head)
{
printf("%d->",head->num);
head = head->next;
}
puts("NUL");
}
void main( void )
{
Node* head1,*head2,*head;
head1 = createTail();
printHead(head1);
head2 = createTail();
printHead(head2);
head = CombinationNode(head1,head2);
printHead(head);
}
//
please enter some digits(end of '.'):
3 2 1 7 9.
List: 3->2->1->7->9->NUL
please enter some digits(end of '.'):
6 4 5 8 7.
List: 6->4->5->8->7->NUL
List: 3->2->1->6->4->5->7->8->7->9->NUL
Press any key to continue
//与上述那段,输出结果一致。
42题的形式变化:
已知两个链表head1 和head2 各自有序,请把它们合并成一个链表依然有序。
//程序三、非递归实现 链表合并排序:
Node * Merge(Node *head1 , Node *head2)
{
if ( head1 == NULL)
return head2 ;
if ( head2 == NULL)
return head1 ;
Node *head = NULL ;
Node *p1 = NULL;
Node *p2 = NULL;
if ( head1->data < head2->data )
{
head = head1 ;
p1 = head1->next;
p2 = head2 ;
}
else
{
head = head2 ;
p2 = head2->next ;
p1 = head1 ;
}
Node *pcurrent = head ;
while ( p1 != NULL && p2 != NULL)
{
if ( p1->data <= p2->data )
{
pcurrent->next = p1 ;
pcurrent = p1 ;
p1 = p1->next ;
}
else
{
pcurrent->next = p2 ;
pcurrent = p2 ;
p2 = p2->next ;
}
}
if ( p1 != NULL )
pcurrent->next = p1 ;
if ( p2 != NULL )
pcurrent->next = p2 ;
return head ;
}
//程序四、递归实现,
Node * MergeRecursive(Node *head1 , Node *head2)
{
if ( head1 == NULL )
return head2 ;
if ( head2 == NULL)
return head1 ;
Node *head = NULL ;
if ( head1->data < head2->data )
{
head = head1 ;
head->next = MergeRecursive(head1->next,head2);
}
else
{
head = head2 ;
head->next = MergeRecursive(head1,head2->next);
}
return head ;
}
--------------------------------------------------------------------------------------------------
ok,最后,咱们来透彻比较下上述几段代码的相同与不同。
不放比较一下,程序一、和程序二关于链表合并的核心代码,的区别:
Node * CombinationNode(Node* head1, Node* head2) //程序二
{
Node *head,*tail,*p = head1,*q = head2,*s;
if( NULL == p )
return q;
if( NULL == q )
return p;
tail = p;
if( p->num > q->num)
tail = q;
head = tail;
while( NULL != p && NULL != q )
{
if(p->num <= q->num )
{
s = p; //3.4
p = p->next; //
}
else
{
s = q;
q = q->next;
}
tail->next = s;
tail = s;
}
if( NULL == p )
p = q;
s = p;
tail->next = s;
return head;
}
和这段:
linklist mergelist(void) //程序一
{
int e,n;
linklist pa,pb,pc,head;
printf("请输入第一个链表的长度:");
scanf("%d",&e);
pa=creatlist(e);
printf("请输入第二个链表的长度:");
scanf("%d",&n);
pb=creatlist(n);
head=pc=(linklist)malloc(sizeof(lnode)); //1.这
pc->next=NULL; //2.这
while(pa&&pb)
{
if(pa->data<=pb->data)
{
pc->next=pa; //3.这
pc=pa;
pa=pa->next;
}
else
{
pc->next=pb; //4.这
pc=pb;
pb=pb->next;
}
}
pc->next=pa?pa:pb;
return head;
}
再比较下,程序一与程序四俩段的形式区别:
linklist mergelist(void)//程序一
{
int e,n;
linklist pa,pb,pc,head;
printf("请输入第一个链表的长度:");
scanf("%d",&e);
pa=creatlist(e);
printf("请输入第二个链表的长度:");
scanf("%d",&n);
pb=creatlist(n);
head=pc=(linklist)malloc(sizeof(lnode));
pc->next=NULL;
while(pa&&pb)
{
if(pa->data<=pb->data)
{
pc->next=pa; //3
pc=pa; //1
pa=pa->next; //2
}
else
{
pc->next=pb;
pc=pb;
pb=pb->next;
}
}
pc->next=pa?pa:pb;
return head;
}
和
//递归实现,程序四
Node * MergeRecursive(Node *head1 , Node *head2)
{
if ( head1 == NULL )
return head2 ;
if ( head2 == NULL)
return head1 ;
Node *head = NULL ;
if ( head1->data < head2->data )
{
head = head1 ;
head->next = MergeRecursive(head1->next,head2);
}
else
{
head = head2 ;
head->next = MergeRecursive(head1,head2->next);
}
return head ;
}
------------------------------
//程序一标明的1、2、3相当于,下述程序四的1、2、3
if ( head1->data < head2->data )
{
head = head1 ; //1.head=head1;
head->next = MergeRecursive(head1->next,head2); //2.head1=head1->next;
//3.head->next=head1
}
else
{
head = head2 ;
head->next = MergeRecursive(head1,head2->next);
}
return head ;
聪明的你,相信,不要我过多解释。:)。
红黑树的C实现完整源码
红黑树C源码实现与剖析
作者:July 、那谁 时间:二零一一年一月三日
-------------------------
前言:
红黑树作为一种经典而高级的数据结构,相信,已经被不少人实现过,但不是因为程序不够完善而无法运行,就是因为程序完全没有注释,初学者根本就看不懂。
此份红黑树的c源码最初从linux-lib-rbtree.c而来,后经一网友那谁(http://www.cppblog.com/converse/)用c写了出来。在此,向原作者表示敬意。但原来的程序存在没有任何一行注释。没有一行注释的程序,令程序的价值大打折扣。
所以,我特把这份源码放到了windows xp+vc 6.0上,一行一行的完善,一行一行的给它添加注释,至此,红黑树c带注释的源码,就摆在了您眼前,有不妥、不正之处,还望不吝指正。
------------
红黑树的六篇文章:
-------------------------
ok,咱们开始吧。
相信,经过我前俩篇博文对红黑树的介绍,你应该对红黑树有了透彻的理解了(没看过的朋友,可事先查上面的倆篇文章,或与此文的源码剖析对应着看)。
本套源码剖析把重点放在红黑树的3种插入情况,与红黑树的4种删除情况。其余的能从略则尽量简略。
目录:
一、左旋代码分析
二、右旋
三、红黑树查找结点
四、红黑树的插入
五、红黑树的3种插入情况
六、红黑树的删除
七、红黑树的4种删除情况
八、测试用例
好的,咱们还是先从树的左旋、右旋代码,开始(大部分分析,直接给注释):
- //一、左旋代码分析
- /*-----------------------------------------------------------
- | node right
- | / / ==> / /
- | a right node y
- | / / / /
- | b y a b //左旋
- -----------------------------------------------------------*/
- static rb_node_t* rb_rotate_left(rb_node_t* node, rb_node_t* root)
- {
- rb_node_t* right = node->right; //指定指针指向 right<--node->right
- if ((node->right = right->left))
- {
- right->left->parent = node; //好比上面的注释图,node成为b的父母
- }
- right->left = node; //node成为right的左孩子
- if ((right->parent = node->parent))
- {
- if (node == node->parent->right)
- {
- node->parent->right = right;
- }
- else
- {
- node->parent->left = right;
- }
- }
- else
- {
- root = right;
- }
- node->parent = right; //right成为node的父母
- return root;
- }
- //二、右旋
- /*-----------------------------------------------------------
- | node left
- | / / / /
- | left y ==> a node
- | / / / /
- | a b b y //右旋与左旋差不多,分析略过
- -----------------------------------------------------------*/
- static rb_node_t* rb_rotate_right(rb_node_t* node, rb_node_t* root)
- {
- rb_node_t* left = node->left;
- if ((node->left = left->right))
- {
- left->right->parent = node;
- }
- left->right = node;
- if ((left->parent = node->parent))
- {
- if (node == node->parent->right)
- {
- node->parent->right = left;
- }
- else
- {
- node->parent->left = left;
- }
- }
- else
- {
- root = left;
- }
- node->parent = left;
- return root;
- }
- //三、红黑树查找结点
- //----------------------------------------------------
- //rb_search_auxiliary:查找
- //rb_node_t* rb_search:返回找到的结点
- //----------------------------------------------------
- static rb_node_t* rb_search_auxiliary(key_t key, rb_node_t* root, rb_node_t** save)
- {
- rb_node_t *node = root, *parent = NULL;
- int ret;
- while (node)
- {
- parent = node;
- ret = node->key - key;
- if (0 < ret)
- {
- node = node->left;
- }
- else if (0 > ret)
- {
- node = node->right;
- }
- else
- {
- return node;
- }
- }
- if (save)
- {
- *save = parent;
- }
- return NULL;
- }
- //返回上述rb_search_auxiliary查找结果
- rb_node_t* rb_search(key_t key, rb_node_t* root)
- {
- return rb_search_auxiliary(key, root, NULL);
- }
- //四、红黑树的插入
- //---------------------------------------------------------
- //红黑树的插入结点
- rb_node_t* rb_insert(key_t key, data_t data, rb_node_t* root)
- {
- rb_node_t *parent = NULL, *node;
- parent = NULL;
- if ((node = rb_search_auxiliary(key, root, &parent))) //调用rb_search_auxiliary找到插入结
- 点的地方
- {
- return root;
- }
- node = rb_new_node(key, data); //分配结点
- node->parent = parent;
- node->left = node->right = NULL;
- node->color = RED;
- if (parent)
- {
- if (parent->key > key)
- {
- parent->left = node;
- }
- else
- {
- parent->right = node;
- }
- }
- else
- {
- root = node;
- }
- return rb_insert_rebalance(node, root); //插入结点后,调用rb_insert_rebalance修复红黑树
- 的性质
- }
- //五、红黑树的3种插入情况
- //接下来,咱们重点分析针对红黑树插入的3种情况,而进行的修复工作。
- //--------------------------------------------------------------
- //红黑树修复插入的3种情况
- //为了在下面的注释中表示方便,也为了让下述代码与我的倆篇文章相对应,
- //用z表示当前结点,p[z]表示父母、p[p[z]]表示祖父、y表示叔叔。
- //--------------------------------------------------------------
- static rb_node_t* rb_insert_rebalance(rb_node_t *node, rb_node_t *root)
- {
- rb_node_t *parent, *gparent, *uncle, *tmp; //父母p[z]、祖父p[p[z]]、叔叔y、临时结点*tmp
- while ((parent = node->parent) && parent->color == RED)
- { //parent 为node的父母,且当父母的颜色为红时
- gparent = parent->parent; //gparent为祖父
- if (parent == gparent->left) //当祖父的左孩子即为父母时。
- //其实上述几行语句,无非就是理顺孩子、父母、祖父的关系。:D。
- {
- uncle = gparent->right; //定义叔叔的概念,叔叔y就是父母的右孩子。
- if (uncle && uncle->color == RED) //情况1:z的叔叔y是红色的
- {
- uncle->color = BLACK; //将叔叔结点y着为黑色
- parent->color = BLACK; //z的父母p[z]也着为黑色。解决z,p[z]都是红色的问题。
- gparent->color = RED;
- node = gparent; //将祖父当做新增结点z,指针z上移俩层,且着为红色。
- //上述情况1中,只考虑了z作为父母的右孩子的情况。
- }
- else //情况2:z的叔叔y是黑色的,
- {
- if (parent->right == node) //且z为右孩子
- {
- root = rb_rotate_left(parent, root); //左旋[结点z,与父母结点]
- tmp = parent;
- parent = node;
- node = tmp; //parent与node 互换角色
- }
- //情况3:z的叔叔y是黑色的,此时z成为了左孩子。
- //注意,1:情况3是由上述情况2变化而来的。
- //......2:z的叔叔总是黑色的,否则就是情况1了。
- parent->color = BLACK; //z的父母p[z]着为黑色
- gparent->color = RED; //原祖父结点着为红色
- root = rb_rotate_right(gparent, root); //右旋[结点z,与祖父结点]
- }
- }
- else
- {
- // if (parent == gparent->right) 当祖父的右孩子即为父母时。(解释请看本文评论下第23楼,同时,感谢SupremeHover指正!)
- uncle = gparent->left; //祖父的左孩子作为叔叔结点。[原理还是与上部分一样的]
- if (uncle && uncle->color == RED) //情况1:z的叔叔y是红色的
- {
- uncle->color = BLACK;
- parent->color = BLACK;
- gparent->color = RED;
- node = gparent; //同上。
- }
- else //情况2:z的叔叔y是黑色的,
- {
- if (parent->left == node) //且z为左孩子
- {
- root = rb_rotate_right(parent, root); //以结点parent、root右旋
- tmp = parent;
- parent = node;
- node = tmp; //parent与node 互换角色
- }
- //经过情况2的变化,成为了情况3.
- parent->color = BLACK;
- gparent->color = RED;
- root = rb_rotate_left(gparent, root); //以结点gparent和root左旋
- }
- }
- }
- root->color = BLACK; //根结点,不论怎样,都得置为黑色。
- return root; //返回根结点。
- }
- //六、红黑树的删除
- //------------------------------------------------------------
- //红黑树的删除结点
- rb_node_t* rb_erase(key_t key, rb_node_t *root)
- {
- rb_node_t *child, *parent, *old, *left, *node;
- color_t color;
- if (!(node = rb_search_auxiliary(key, root, NULL))) //调用rb_search_auxiliary查找要删除的
- 结点
- {
- printf("key %d is not exist!/n");
- return root;
- }
- old = node;
- if (node->left && node->right)
- {
- node = node->right;
- while ((left = node->left) != NULL)
- {
- node = left;
- }
- child = node->right;
- parent = node->parent;
- color = node->color;
- if (child)
- {
- child->parent = parent;
- }
- if (parent)
- {
- if (parent->left == node)
- {
- parent->left = child;
- }
- else
- {
- parent->right = child;
- }
- }
- else
- {
- root = child;
- }
- if (node->parent == old)
- {
- parent = node;
- }
- node->parent = old->parent;
- node->color = old->color;
- node->right = old->right;
- node->left = old->left;
- if (old->parent)
- {
- if (old->parent->left == old)
- {
- old->parent->left = node;
- }
- else
- {
- old->parent->right = node;
- }
- }
- else
- {
- root = node;
- }
- old->left->parent = node;
- if (old->right)
- {
- old->right->parent = node;
- }
- }
- else
- {
- if (!node->left)
- {
- child = node->right;
- }
- else if (!node->right)
- {
- child = node->left;
- }
- parent = node->parent;
- color = node->color;
- if (child)
- {
- child->parent = parent;
- }
- if (parent)
- {
- if (parent->left == node)
- {
- parent->left = child;
- }
- else
- {
- parent->right = child;
- }
- }
- else
- {
- root = child;
- }
- }
- free(old);
- if (color == BLACK)
- {
- root = rb_erase_rebalance(child, parent, root); //调用rb_erase_rebalance来恢复红黑树性
- 质
- }
- return root;
- }
- //七、红黑树的4种删除情况
- //----------------------------------------------------------------
- //红黑树修复删除的4种情况
- //为了表示下述注释的方便,也为了让下述代码与我的倆篇文章相对应,
- //x表示要删除的结点,*other、w表示兄弟结点,
- //----------------------------------------------------------------
- static rb_node_t* rb_erase_rebalance(rb_node_t *node, rb_node_t *parent, rb_node_t *root)
- {
- rb_node_t *other, *o_left, *o_right; //x的兄弟*other,兄弟左孩子*o_left,*o_right
- while ((!node || node->color == BLACK) && node != root)
- {
- if (parent->left == node)
- {
- other = parent->right;
- if (other->color == RED) //情况1:x的兄弟w是红色的
- {
- other->color = BLACK;
- parent->color = RED; //上俩行,改变颜色,w->黑、p[x]->红。
- root = rb_rotate_left(parent, root); //再对p[x]做一次左旋
- other = parent->right; //x的新兄弟new w 是旋转之前w的某个孩子。其实就是左旋后
- 的效果。
- }
- if ((!other->left || other->left->color == BLACK) &&
- (!other->right || other->right->color == BLACK))
- //情况2:x的兄弟w是黑色,且w的俩个孩子也
- 都是黑色的
- { //由于w和w的俩个孩子都是黑色的,则在x和w上得去掉一黑色,
- other->color = RED; //于是,兄弟w变为红色。
- node = parent; //p[x]为新结点x
- parent = node->parent; //x<-p[x]
- }
- else //情况3:x的兄弟w是黑色的,
- { //且,w的左孩子是红色,右孩子为黑色。
- if (!other->right || other->right->color == BLACK)
- {
- if ((o_left = other->left)) //w和其左孩子left[w],颜色交换。
- {
- o_left->color = BLACK; //w的左孩子变为由黑->红色
- }
- other->color = RED; //w由黑->红
- root = rb_rotate_right(other, root); //再对w进行右旋,从而红黑性质恢复。
- other = parent->right; //变化后的,父结点的右孩子,作为新的兄弟结点
- w。
- }
- //情况4:x的兄弟w是黑色的
- other->color = parent->color; //把兄弟节点染成当前节点父节点的颜色。
- parent->color = BLACK; //把当前节点父节点染成黑色
- if (other->right) //且w的右孩子是红
- {
- other->right->color = BLACK; //兄弟节点w右孩子染成黑色
- }
- root = rb_rotate_left(parent, root); //并再做一次左旋
- node = root; //并把x置为根。
- break;
- }
- }
- //下述情况与上述情况,原理一致。分析略。
- else
- {
- other = parent->left;
- if (other->color == RED)
- {
- other->color = BLACK;
- parent->color = RED;
- root = rb_rotate_right(parent, root);
- other = parent->left;
- }
- if ((!other->left || other->left->color == BLACK) &&
- (!other->right || other->right->color == BLACK))
- {
- other->color = RED;
- node = parent;
- parent = node->parent;
- }
- else
- {
- if (!other->left || other->left->color == BLACK)
- {
- if ((o_right = other->right))
- {
- o_right->color = BLACK;
- }
- other->color = RED;
- root = rb_rotate_left(other, root);
- other = parent->left;
- }
- other->color = parent->color;
- parent->color = BLACK;
- if (other->left)
- {
- other->left->color = BLACK;
- }
- root = rb_rotate_right(parent, root);
- node = root;
- break;
- }
- }
- }
- if (node)
- {
- node->color = BLACK; //最后将node[上述步骤置为了根结点],改为黑色。
- }
- return root; //返回root
- }
- //八、测试用例
- //主函数
- int main()
- {
- int i, count = 100;
- key_t key;
- rb_node_t* root = NULL, *node = NULL;
- srand(time(NULL));
- for (i = 1; i < count; ++i)
- {
- key = rand() % count;
- if ((root = rb_insert(key, i, root)))
- {
- printf("[i = %d] insert key %d success!/n", i, key);
- }
- else
- {
- printf("[i = %d] insert key %d error!/n", i, key);
- exit(-1);
- }
- if ((node = rb_search(key, root)))
- {
- printf("[i = %d] search key %d success!/n", i, key);
- }
- else
- {
- printf("[i = %d] search key %d error!/n", i, key);
- exit(-1);
- }
- if (!(i % 10))
- {
- if ((root = rb_erase(key, root)))
- {
- printf("[i = %d] erase key %d success/n", i, key);
- }
- else
- {
- printf("[i = %d] erase key %d error/n", i, key);
- }
- }
- }
- return 0;
- }
ok,完。
后记:
一、欢迎任何人就此份源码,以及我的前述倆篇文章,进行讨论、提议。
但任何人,引用此份源码剖析,必须得注明作者本人July以及出处。
红黑树系列,已经写了三篇文章,相信,教你透彻了解红黑树的目的,应该达到了。
二、本文完整源码,请到此处下载:
微软等数据结构+算法面试100题[第41-60题答案]
[最新答案V0.4版]微软等数据结构+算法面试100题[第41-60题答案]
作者 July、Csdn网友
二零一一年一月四日
------------------------------------------------
想说的第一句话是,终于更新了。
整理此面试100题的答案毕竟不是一件轻松的事。
但,无论如何,我至始至终坚持下来了。
ok,长话短说,此微软等面试100题系列,的的确确有上十万人看到或见识过了。
相信,大家都知道它的潜力以及给面试者、初学者带来的好处。
目前,本人正在积极准备精选微软等公司数据结构+算法面试100题系列V0.2版,
打算把它当做一个永久的项目,长期做下去。
欢迎,对解这类面试题有兴趣的人,加入我们,一起整理面试100题V0.2版,
或者参与V0.1版答案的解决、与维护。
永远,欢迎,各位,就这微软等100题系列,提出你对任何一道面试题的思路,
或者,加入我们,一起交流。[我们的交流圈子:qq群,69809881]
微软等100题系列V0.1版答案V0.4版第41-60题的答案,已经上传,
欢迎各位从下链接处下载(注:此答案系列只能作为你的参考):
[最新答案V0.4版]微软等数据结构+算法面试100题[第41-60题答案]
http://download.csdn.net/source/2959162
更多资源,下载地址:
http://v_july_v.download.csdn.net/
快速排序算法
作者 July 二零一一年一月四日
------------------------------------------
写之前,先说点题外话。
每写一篇文章,我都会遵循以下几点原则:
一、保持版面的尽量清晰,力保排版良好。
二、力争所写的东西,清晰易懂,图文并茂
三、尽最大可能确保所写的东西精准,有实用价值。
因为,我觉得,你既然要把你的文章,公布出来,那么你就一定要为你的读者负责。
不然,就不要发表出来。一切,为读者服务。
ok,闲不多说。接下来,咱们立刻进入本文章的主题,排序算法。
众所周知,快速排序算法是排序算法中的重头戏。
因此,本系列,本文就从快速排序开始。
------------------------------------------------------
一、快速排序算法的基本特性
时间复杂度:O(n*lgn)
最坏:O(n^2)
空间复杂度:O(n*lgn)
不稳定。
快速排序是一种排序算法,对包含n个数的输入数组,平均时间为O(nlgn),最坏情况是O(n^2)。
通常是用于排序的最佳选择。因为,排序最快,也只能达到O(nlgn)。
二、快速排序算法的描述
算法导论,第7章
快速排序时基于分治模式处理的,
对一个典型子数组A[p...r]排序的分治过程为三个步骤:
1.分解:
A[p..r]被划分为俩个(可能空)的子数组A[p ..q-1]和A[q+1 ..r],使得
A[p ..q-1] <= A[q] <= A[q+1 ..r]
2.解决:通过递归调用快速排序,对子数组A[p ..q-1]和A[q+1 ..r]排序。
3.合并。
三、快速排序算法
版本一:
QUICKSORT(A, p, r)
1 if p < r
2 then q ← PARTITION(A, p, r) //关键
3 QUICKSORT(A, p, q - 1)
4 QUICKSORT(A, q + 1, r)
数组划分
快速排序算法的关键是PARTITION过程,它对A[p..r]进行就地重排:
PARTITION(A, p, r)
1 x ← A[r]
2 i ← p - 1
3 for j ← p to r - 1
4 do if A[j] ≤ x
5 then i ← i + 1
6 exchange A[i] <-> A[j]
7 exchange A[i + 1] <-> A[r]
8 return i + 1
ok,咱们来举一个具体而完整的例子。
来对以下数组,进行快速排序,
2 8 7 1 3 5 6 4(主元)
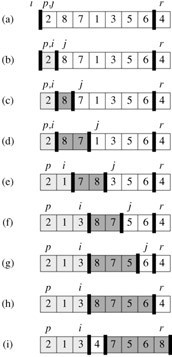
一、
i p/j
2 8 7 1 3 5 6 4(主元)
j指的2<=4,于是i++,i也指到2,2和2互换,原数组不变。
j后移,直到指向1..
二、
j(指向1)<=4,于是i++
i指向了8,所以8与1交换。
数组变成了:
i j
2 1 7 8 3 5 6 4
三、j后移,指向了3,3<=4,于是i++
i这是指向了7,于是7与3交换。
数组变成了:
i j
2 1 3 8 7 5 6 4
四、j继续后移,发现没有再比4小的数,所以,执行到了最后一步,
即上述PARTITION(A, p, r)代码部分的 第7行。
因此,i后移一个单位,指向了8
i j
2 1 3 8 7 5 6 4
A[i + 1] <-> A[r],即8与4交换,所以,数组最终变成了如下形式,
2 1 3 4 7 5 6 8
ok,快速排序第一趟完成。
4把整个数组分成了俩部分,2 1 3,7 5 6 8,再递归对这俩部分分别快速排序。
i p/j
2 1 3(主元)
2与2互换,不变,然后又是1与1互换,还是不变,最后,3与3互换,不变,
最终,3把2 1 3,分成了俩部分,2 1,和3.
再对2 1,递归排序,最终结果成为了1 2 3.
7 5 6 8(主元),7、5、6、都比8小,所以第一趟,还是7 5 6 8,
不过,此刻8把7 5 6 8,分成了 7 5 6,和8.[7 5 6->5 7 6->5 6 7]
再对7 5 6,递归排序,最终结果变成5 6 7 8。
ok,所有过程,全部分析完成。
最后,看下我画的图:

快速排序算法版本二
不过,这个版本不再选取(如上第一版本的)数组的最后一个元素为主元,
而是选择,数组中的第一个元素为主元。
/**************************************************/
/* 函数功能:快速排序算法 */
/* 函数参数:结构类型table的指针变量tab */
/* 整型变量left和right左右边界的下标 */
/* 函数返回值:空 */
/* 文件名:quicsort.c 函数名:quicksort () */
/**************************************************/
void quicksort(table *tab,int left,int right)
{
int i,j;
if(left<right)
{
i=left;j=right;
tab->r[0]=tab->r[i]; //准备以本次最左边的元素值为标准进行划分,先保存其值
do
{
while(tab->r[j].key>tab->r[0].key&&i<j)
j--; //从右向左找第1个小于标准值的位置j
if(i<j) //找到了,位置为j
{
tab->r[i].key=tab->r[j].key;i++;
} //将第j个元素置于左端并重置i
while(tab->r[i].key<tab->r[0].key&&i<j)
i++; //从左向右找第1个大于标准值的位置i
if(i<j) //找到了,位置为i
{
tab->r[j].key=tab->r[i].key;j--;
} //将第i个元素置于右端并重置j
}while(i!=j);
tab->r[i]=tab->r[0]; //将标准值放入它的最终位置,本次划分结束
quicksort(tab,left,i-1); //对标准值左半部递归调用本函数
quicksort(tab,i+1,right); //对标准值右半部递归调用本函数
}
}
----------------
ok,咱们,还是以上述相同的数组,应用此快排算法的版本二,来演示此排序过程:
这次,以数组中的第一个元素2为主元。
2(主) 8 7 1 3 5 6 4
请细看:
2 8 7 1 3 5 6 4
i-> <-j
(找大) (找小)
一、j
j找第一个小于2的元素1,1赋给(覆盖重置)i所指元素2
得到:
1 8 7 3 5 6 4
i j
二、i
i找到第一个大于2的元素8,8赋给(覆盖重置)j所指元素(NULL<-8)
1 7 8 3 5 6 4
i <-j
三、j
j继续左移,在与i碰头之前,没有找到比2小的元素,结束。
最后,主元2补上。
第一趟快排结束之后,数组变成:
1 2 7 8 3 5 6 4
第二趟,
7 8 3 5 6 4
i-> <-j
(找大) (找小)
一、j
j找到4,比主元7小,4赋给7所处位置
得到:
4 8 3 5 6
i-> j
二、i
i找比7大的第一个元素8,8覆盖j所指元素(NULL)
4 3 5 6 8
i j
4 6 3 5 8
i-> j
i与j碰头,结束。
第三趟:
4 6 3 5 7 8
......
以下,分析原理,一致,略过。
最后的结果,如下图所示:
1 2 3 4 5 6 7 8
相信,经过以上内容的具体分析,你一定明了了。
最后,贴一下我画的关于这个排序过程的图:


完。一月五日补充。
OK,上述俩种算法,明白一种即可。
-------------------------------------------------------------
五、快速排序的最坏情况和最快情况。
最坏情况发生在划分过程产生的俩个区域分别包含n-1个元素和一个0元素的时候,
即假设算法每一次递归调用过程中都出现了,这种划分不对称。那么划分的代价为O(n),
因为对一个大小为0的数组递归调用后,返回T(0)=O(1)。
估算法的运行时间可以递归的表示为:
T(n)=T(n-1)+T(0)+O(n)=T(n-1)+O(n).
可以证明为T(n)=O(n^2)。
因此,如果在算法的每一层递归上,划分都是最大程度不对称的,那么算法的运行时间就是O(n^2)。
亦即,快速排序算法的最坏情况并不比插入排序的更好。
此外,当数组完全排好序之后,快速排序的运行时间为O(n^2)。
而在同样情况下,插入排序的运行时间为O(n)。
//注,请注意理解这句话。我们说一个排序的时间复杂度,是仅仅针对一个元素的。
//意思是,把一个元素进行插入排序,即把它插入到有序的序列里,花的时间为n。
再来证明,最快情况下,即PARTITION可能做的最平衡的划分中,得到的每个子问题都不能大于n/2.
因为其中一个子问题的大小为|_n/2_|。另一个子问题的大小为|-n/2-|-1.
在这种情况下,快速排序的速度要快得多。为,
T(n)<=2T(n/2)+O(n).可以证得,T(n)=O(nlgn)。
直观上,看,快速排序就是一颗递归数,其中,PARTITION总是产生9:1的划分,
总的运行时间为O(nlgn)。各结点中示出了子问题的规模。每一层的代价在右边显示。
每一层包含一个常数c。
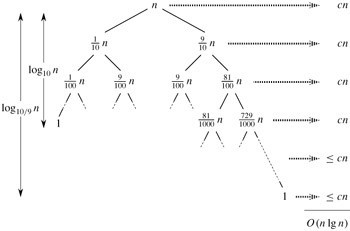
完。
July、二零一一年一月四日。
=============================================
请各位自行,思考以下这个版本,对应于上文哪个版本?
HOARE-PARTITION(A, p, r)
1 x ← A[p]
2 i ← p - 1
3 j ← r + 1
4 while TRUE
5 do repeat j ← j - 1
6 until A[j] ≤ x
7 repeat i ← i + 1
8 until A[i] ≥ x
9 if i < j
10 then exchange A[i] ↔ A[j]
11 else return j
我常常思考,为什么有的人当时明明读懂明白了一个算法,
而一段时间过后,它又对此算法完全陌生而不了解了列?
我想,究其根本,还是没有彻底明白此快速排序算法的原理,与来龙去脉...
那作何改进列,只能找发明那个算法的原作者了,从原作者身上,再多挖掘点有用的东西出来。
July、二零一一年二月十五日更新。
=========================================
最后,再给出一个快速排序算法的简洁示例:
Quicksort函数
void quicksort(int l, int u)
{ int i, m;
if (l >= u) return;
swap(l, randint(l, u));
m = l;
for (i = l+1; i <= u; i++)
if (x[i] < x[l])
swap(++m, i);
swap(l, m);
quicksort(l, m-1);
quicksort(m+1, u);
}
如果函数的调用形式是quicksort(0, n-1),那么这段代码将对一个全局数组x[n]进行排序。
函数的两个参数分别是将要进行排序的子数组的下标:l是较低的下标,而u是较高的下标。
函数调用swap(i,j)将会交换x[i]与x[j]这两个元素。
第一次交换操作将会按照均匀分布的方式在l和u之间随机地选择一个划分元素。
程序员的美:极致与疯狂
程序员的美:极致与疯狂
作者:July 二零一一年一月五日
---------------------------------------------
一、程序员的追求之美
1、把一件简单的事,做到极致,便是一种美,更是一种疯狂。
2、为了完善一个小的细节问题,不惜推倒重来,这是一种勇气与气量。
3、有时候,性格的偏执不是一种缺陷,而是一种态度,包括对人、和处事。
4、这个世界上,追不到女孩子,并不丢脸,丢脸的是,不敢去追求自己钟情的东西。
5、有的时候,客户是上帝,有的时候,上帝也是不仁慈的,它会百般刁难你。
6、人们不在乎,你的工作有多艰难,人们只在乎,他们用的东西,好不好。
7、孤独是一种美,孤独也是一种信仰。
8、不把它做出来,放心不下,不把它完善,良心不安。
9、很多时候,很多的事,不带目的,不带追求,仅仅只是一种自娱自乐而已。
10、哪一天,他们不再写程序了,可能是因为他们的手指敲不动键盘了。
二、程序员的灵魂之美
贝多芬曾说,只有音乐家才能接近上帝。可惜,他错了,这个世界上,还有另外一种职业。
同样是以上帝的名义,深夜里,独自对着自己的灵魂静语,如云动,如水流。
而电脑上,那一行一行美到极致处的代码,便是他们用来与上帝交流的语言,
就在那无数个深夜,那无数个无声、只有键盘敲打、鼠标点击的日子里。
音乐家,弹奏钢琴,奏出美妙的音符,
程序员,敲打键盘,编写美妙的代码。
一种音符,一种代码,同是行云流水,同等令人舒畅。
完。
-------------------------------
一步一图一代码,一定要让你真正彻底明白红黑树
一步一图一代码,一定要让你真正彻底明白红黑树
作者:July 二零一一年一月九日
-----------------------------
本文参考:
I、 The Art of Computer Programming Volume I
II、 Introduction to Algorithms, Second Edition
III、The Annotated STL Sources
IV、 Wikipedia
V、 Algorithms In C Third Edition
VI、 本人写的关于红黑树的前三篇文章:
第一篇:教你透彻了解红黑树:
http://blog.csdn.net/v_JULY_v/archive/2010/12/29/6105630.aspx
第二篇:红黑树算法的层层剖析与逐步实现
http://blog.csdn.net/v_JULY_v/archive/2010/12/31/6109153.aspx
第三篇:教你彻底实现红黑树:红黑树的c源码实现与剖析
http://blog.csdn.net/v_JULY_v/archive/2011/01/03/6114226.aspx
---------------------------------------------
前言:
1、有读者反应,说看了我的前几篇文章,对红黑树的了解还是不够透彻。
2、我个人觉得,如果我一步一步,用图+代码来阐述各种插入、删除情况,可能会更直观易懂。
3、既然写了红黑树,那么我就一定要把它真正写好,让读者真正彻底明白红黑树。
本文相对我前面红黑树相关的3篇文章,主要有以下几点改进:
1.图、文字叙述、代码编写,彼此对应,明朗而清晰。
2.宏观总结,红黑树的性质与插入、删除情况的认识。
3.代码来的更直接,结合图,给你最直观的感受,彻底明白红黑树。
ok,首先,以下几点,你现在应该是要清楚明白了的:
I、红黑树的五个性质:
1)每个结点要么是红的,要么是黑的。
2)根结点是黑的。
3)每个叶结点,即空结点(NIL)是黑的。
4)如果一个结点是红的,那么它的俩个儿子都是黑的。
5)对每个结点,从该结点到其子孙结点的所有路径上包含相同数目的黑结点。
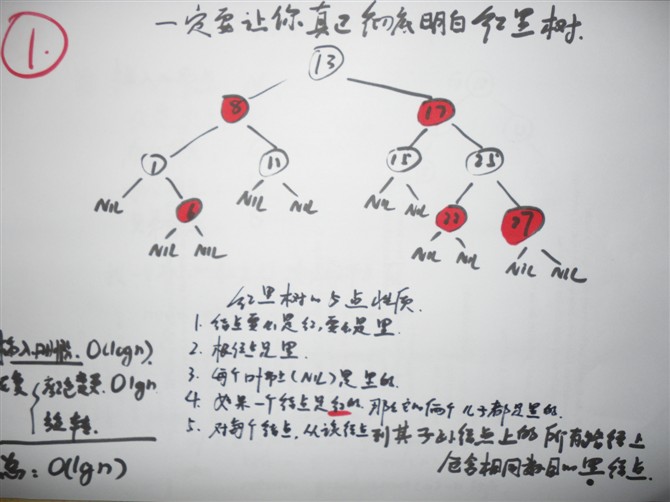
II、红黑树插入的几种情况:
情况1,z的叔叔y是红色的。
情况2:z的叔叔y是黑色的,且z是右孩子
情况3:z的叔叔y是黑色的,且z是左孩子
III、红黑树删除的几种情况。
情况1:x的兄弟w是红色的。
情况2:x的兄弟w是黑色的,且w的俩个孩子都是黑色的。
情况3:x的兄弟w是黑色的,且w的左孩子是红色,w的右孩子是黑色。
情况4:x的兄弟w是黑色的,且w的右孩子是红色的。
除此之外,还得明确一点:
IV、我们知道,红黑树插入、或删除结点后,
可能会违背、或破坏红黑树的原有的性质,
所以为了使插入、或删除结点后的树依然维持为一棵新的红黑树,
那就要做俩方面的工作:
1、部分结点颜色,重新着色
2、调整部分指针的指向,即左旋、右旋。
V、并区别以下俩种操作:
1)红黑树插入、删除结点的操作,RB-INSERT(T, z),RB-DELETE(T, z)
2).红黑树已经插入、删除结点之后,
为了保持红黑树原有的红黑性质而做的恢复与保持红黑性质的操作。
如RB-INSERT-FIXUP(T, z),RB-DELETE-FIXUP(T, x)
以上这5点,我已经在我前面的2篇文章,都已阐述过不少次了,希望,你现在已经透彻明了。
---------------------------------------------------------------------
本文,着重图解分析红黑树插入、删除结点后为了维持红黑性质而做修复工作的各种情况。
[下文各种插入、删除的情况,与我的第二篇文章,红黑树算法的实现与剖析相对应]
ok,开始。
一、在下面的分析中,我们约定:
要插入的节点为,N
父亲节点,P
祖父节点,G
叔叔节点,U
兄弟节点,S
如下图所示,找一个节点的祖父和叔叔节点:
node grandparent(node n) //祖父
{
return n->parent->parent;
}
node uncle(node n) //叔叔
{
if (n->parent == grandparent(n)->left)
return grandparent(n)->right;
else
return grandparent(n)->left;
}

二、红黑树插入的几种情况
情形1: 新节点N位于树的根上,没有父节点
void insert_case1(node n) {
if (n->parent == NULL)
n->color = BLACK;
else
insert_case2(n);
}
情形2: 新节点的父节点P是黑色
void insert_case2(node n) {
if (n->parent->color == BLACK)
return; /* 树仍旧有效 */
else
insert_case3(n);
}

情形3:父节点P、叔叔节点U,都为红色,
[对应第二篇文章中,的情况1:z的叔叔是红色的。]
void insert_case3(node n) {
if (uncle(n) != NULL && uncle(n)->color == RED) {
n->parent->color = BLACK;
uncle(n)->color = BLACK;
grandparent(n)->color = RED;
insert_case1(grandparent(n)); //因为祖父节点可能是红色的,违反性质4,递归情形1.
}
else
insert_case4(n); //否则,叔叔是黑色的,转到下述情形4处理。

此时新插入节点N做为P的左子节点或右子节点都属于上述情形3,上图仅显示N做为P左子的情形。
情形4: 父节点P是红色,叔叔节点U是黑色或NIL;
插入节点N是其父节点P的右孩子,而父节点P又是其父节点的左孩子。
[对应我第二篇文章中,的情况2:z的叔叔是黑色的,且z是右孩子]
void insert_case4(node n) {
if (n == n->parent->right && n->parent == grandparent(n)->left) {
rotate_left(n->parent);
n = n->left;
} else if (n == n->parent->left && n->parent == grandparent(n)->right) {
rotate_right(n->parent);
n = n->right;
}
insert_case5(n); //转到下述情形5处理。
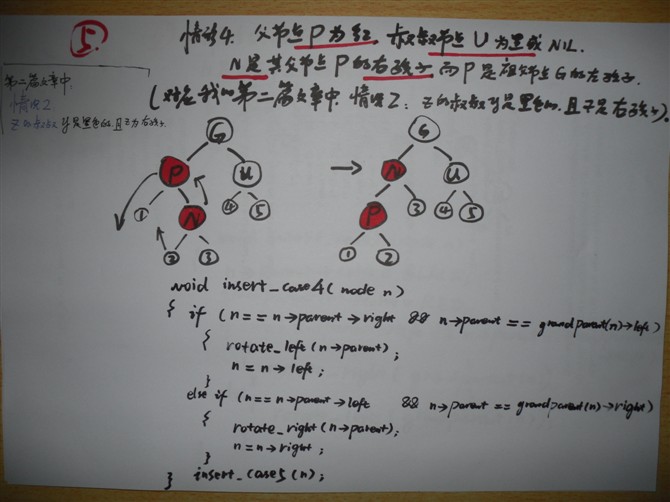
情形5: 父节点P是红色,而叔父节点U 是黑色或NIL,
要插入的节点N 是其父节点的左孩子,而父节点P又是其父G的左孩子。
[对应我第二篇文章中,情况3:z的叔叔是黑色的,且z是左孩子。]
void insert_case5(node n) {
n->parent->color = BLACK;
grandparent(n)->color = RED;
if (n == n->parent->left && n->parent == grandparent(n)->left) {
rotate_right(grandparent(n));
} else {
/* 反情况,N 是其父节点的右孩子,而父节点P又是其父G的右孩子 */
rotate_left(grandparent(n));
}
}

三、红黑树删除的几种情况
上文我们约定,兄弟节点设为S,我们使用下述函数找到兄弟节点:
struct node * sibling(struct node *n) //找兄弟节点
{
if (n == n->parent->left)
return n->parent->right;
else
return n->parent->left;
}
情况1: N 是新的根。
void
delete_case1(struct node *n)
{
if (n->parent != NULL)
delete_case2(n);
}

情形2:兄弟节点S是红色
[对应我第二篇文章中,情况1:x的兄弟w是红色的。]
void delete_case2(struct node *n)
{
struct node *s = sibling(n);
if (s->color == RED) {
n->parent->color = RED;
s->color = BLACK;
if (n == n->parent->left)
rotate_left(n->parent); //左旋
else
rotate_right(n->parent);
}
delete_case3(n);
}
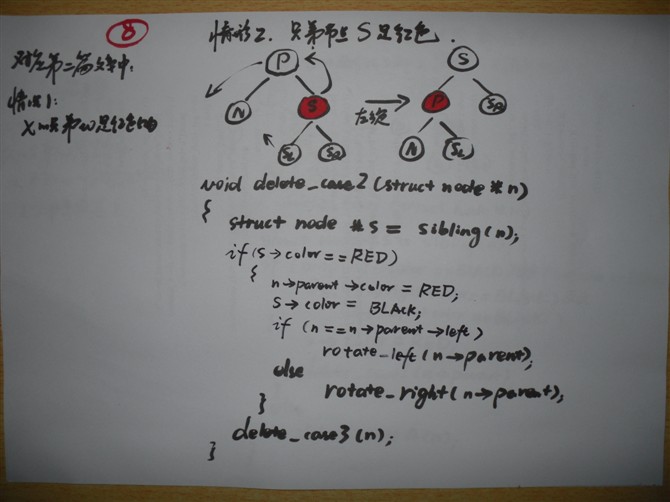
情况 3: 兄弟节点S是黑色的,且S的俩个儿子都是黑色的。但N的父节点P,是黑色。
[对应我第二篇文章中,情况2:x的兄弟w是黑色的,且兄弟w的俩个儿子都是黑色的。
(这里,父节点P为黑)]
void delete_case3(struct node *n)
{
struct node *s = sibling(n);
if ((n->parent->color == BLACK) &&
(s->color == BLACK) &&
(s->left->color == BLACK) &&
(s->right->color == BLACK)) {
s->color = RED;
delete_case1(n->parent);
} else
delete_case4(n);
}
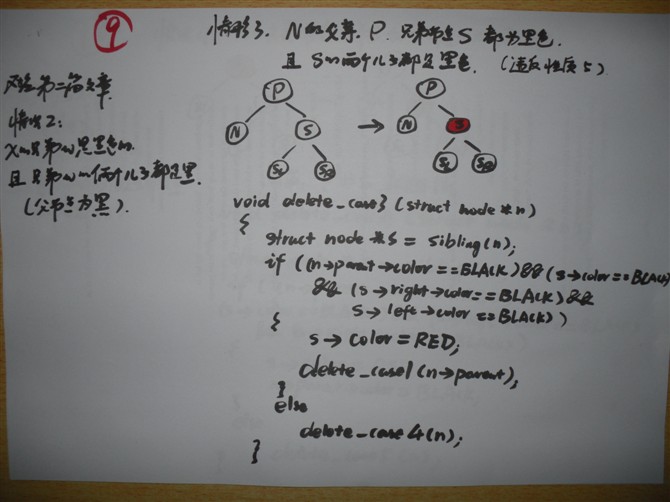
情况4: 兄弟节点S 是黑色的、S 的儿子也都是黑色的,但是 N 的父亲P,是红色。
[还是对应我第二篇文章中,情况2:x的兄弟w是黑色的,且w的俩个孩子都是黑色的。
(这里,父节点P为红)]
void delete_case4(struct node *n)
{
struct node *s = sibling(n);
if ((n->parent->color == RED) &&
(s->color == BLACK) &&
(s->left->color == BLACK) &&
(s->right->color == BLACK)) {
s->color = RED;
n->parent->color = BLACK;
} else
delete_case5(n);
}
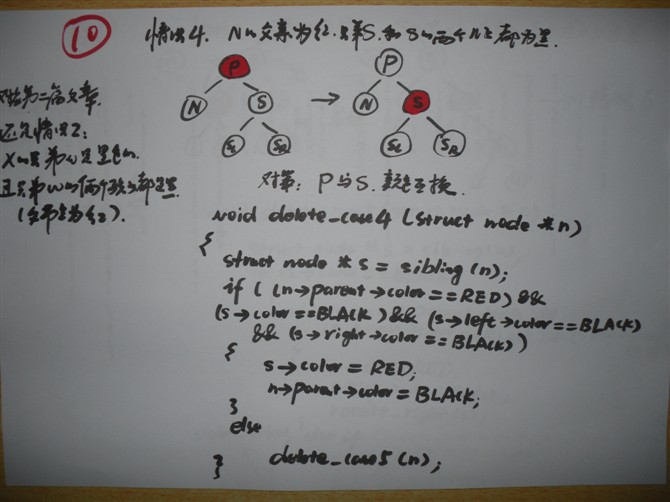
情况5: 兄弟S为黑色,S 的左儿子是红色,S 的右儿子是黑色,而N是它父亲的左儿子。
//此种情况,最后转化到下面的情况6。
[对应我第二篇文章中,情况3:x的兄弟w是黑色的,w的左孩子是红色,w的右孩子是黑色。]
void delete_case5(struct node *n)
{
struct node *s = sibling(n);
if (s->color == BLACK)
if ((n == n->parent->left) &&
(s->right->color == BLACK) &&
(s->left->color == RED)) {
// this last test is trivial too due to cases 2-4.
s->color = RED;
s->left->color = BLACK;
rotate_right(s);
} else if ((n == n->parent->right) &&
(s->left->color == BLACK) &&
(s->right->color == RED)) {
// this last test is trivial too due to cases 2-4.
s->color = RED;
s->right->color = BLACK;
rotate_left(s);
}
}
delete_case6(n); //转到情况6。
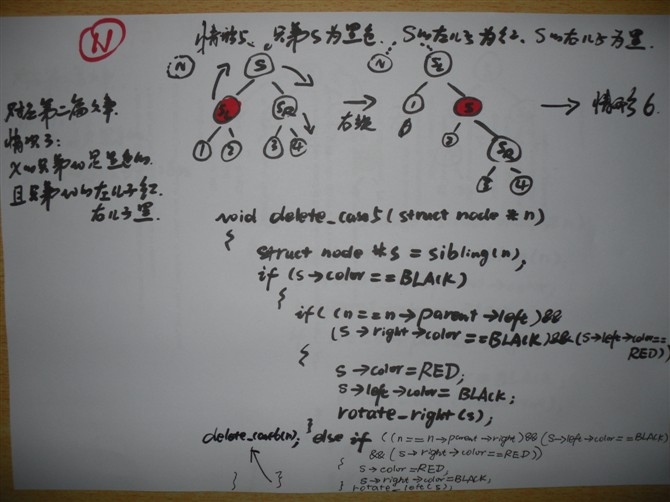
情况6: 兄弟节点S是黑色,S的右儿子是红色,而 N 是它父亲的左儿子。
[对应我第二篇文章中,情况4:x的兄弟w是黑色的,且w的右孩子时红色的。]
void delete_case6(struct node *n)
{
struct node *s = sibling(n);
s->color = n->parent->color;
n->parent->color = BLACK;
if (n == n->parent->left) {
s->right->color = BLACK;
rotate_left(n->parent);
} else {
s->left->color = BLACK;
rotate_right(n->parent);
}
}
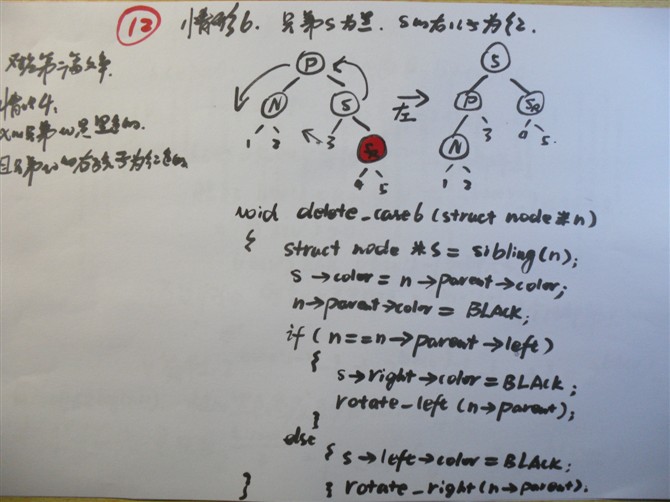
//呵呵,画这12张图,直接从中午画到了晚上。希望,此文能让你明白。
四、红黑树的插入、删除情况时间复杂度的分析
因为每一个红黑树也是一个特化的二叉查找树,
因此红黑树上的只读操作与普通二叉查找树上的只读操作相同。
然而,在红黑树上进行插入操作和删除操作会导致不再符合红黑树的性质。
恢复红黑树的属性需要少量(O(log n))的颜色变更(实际是非常快速的)和
不超过三次树旋转(对于插入操作是两次)。
虽然插入和删除很复杂,但操作时间仍可以保持为 O(log n) 次。

ok,完。
后记:
此红黑树系列,前前后后,已经写了4篇文章,如果读者读完了这4篇文章,
对红黑树有一个相对之前来说,比较透彻的理解,
那么,也不枉费,我花这么多篇幅、花好几个钟头去画红黑树了。
真正理解一个数据结构、算法,最紧要的还是真正待用、实践的时候体会。
欢迎,各位,将现在、或以后学习、工作中运用此红黑树结构、算法的经验与我分享。
谢谢。:D。
----------------------------------------
永久勘误:微软等面试100题答案V0.2版[第1-20题答案]
作者:July 、何海涛等网友
---------------------------
开诚布公,接受读者检验
本文,是根据我之前上传的,微软等面试100题,的答案V0.2版[第1-20题答案]的部分答案精选,
此后来不断的粗略的看了看,发现这些答案大部分都有可取之处,但存在的小问题还是不少。
所以,特意把之前上传的答案V0.2版,中部分精彩、和有争议的答案,开诚布公,
放到我的博客上,给读者除了帖子外,多提供一个反馈与交流的机会。
要感谢很多的网友,在此,就不一一列出了。
ok,话不絮烦。
此文永久勘误,永久优化。各位,对以下任何一题的答案有任何问题,请把您的意见回复于此贴上:本微软等100题系列V0.1版,永久维护(网友,思路回复)地址:
http://topic.csdn.net/u/20101126/10/b4f12a00-6280-492f-b785-cb6835a63dc9.html
2010年 10月18日下午 July
--------------------------------
1.把二元查找树转变成排序的双向链表
题目:
输入一棵二元查找树,将该二元查找树转换成一个排序的双向链表。
要求不能创建任何新的结点,只调整指针的指向。
10
/ /
6 14
/ / / /
4 8 12 16
转换成双向链表
4=6=8=10=12=14=16。
首先我们定义的二元查找树 节点的数据结构如下:
struct BSTreeNode
{
int m_nValue; // value of node
BSTreeNode *m_pLeft; // left child of node
BSTreeNode *m_pRight; // right child of node
};
//引用 245 楼 tree_star 的回复
#include <stdio.h>
#include <iostream.h>
struct BSTreeNode
{
int m_nValue; // value of node
BSTreeNode *m_pLeft; // left child of node
BSTreeNode *m_pRight; // right child of node
};
typedef BSTreeNode DoubleList;
DoubleList * pHead;
DoubleList * pListIndex;
void convertToDoubleList(BSTreeNode * pCurrent);
// 创建二元查找树
void addBSTreeNode(BSTreeNode * & pCurrent, int value)
{
if (NULL == pCurrent)
{
BSTreeNode * pBSTree = new BSTreeNode();
pBSTree->m_pLeft = NULL;
pBSTree->m_pRight = NULL;
pBSTree->m_nValue = value;
pCurrent = pBSTree;
}
else
{
if ((pCurrent->m_nValue) > value)
{
addBSTreeNode(pCurrent->m_pLeft, value);
}
else if ((pCurrent->m_nValue) < value)
{
addBSTreeNode(pCurrent->m_pRight, value);
}
else
{
//cout<<"重复加入节点"<<endl;
}
}
}
// 遍历二元查找树 中序
void ergodicBSTree(BSTreeNode * pCurrent)
{
if (NULL == pCurrent)
{
return;
}
if (NULL != pCurrent->m_pLeft)
{
ergodicBSTree(pCurrent->m_pLeft);
}
// 节点接到链表尾部
convertToDoubleList(pCurrent);
// 右子树为空
if (NULL != pCurrent->m_pRight)
{
ergodicBSTree(pCurrent->m_pRight);
}
}
// 二叉树转换成list
void convertToDoubleList(BSTreeNode * pCurrent)
{
pCurrent->m_pLeft = pListIndex;
if (NULL != pListIndex)
{
pListIndex->m_pRight = pCurrent;
}
else
{
pHead = pCurrent;
}
pListIndex = pCurrent;
cout<<pCurrent->m_nValue<<endl;
}
int main()
{
BSTreeNode * pRoot = NULL;
pListIndex = NULL;
pHead = NULL;
addBSTreeNode(pRoot, 10);
addBSTreeNode(pRoot, 4);
addBSTreeNode(pRoot, 6);
addBSTreeNode(pRoot, 8);
addBSTreeNode(pRoot, 12);
addBSTreeNode(pRoot, 14);
addBSTreeNode(pRoot, 15);
addBSTreeNode(pRoot, 16);
ergodicBSTree(pRoot);
return 0;
}
///
4
6
8
10
12
14
15
16
Press any key to continue
//
--------------------------------------------------------------
同样是上道题,再给各位看一段简洁的代码:
void change(Node *p, Node *&last) //中序遍历
{
if (!p)
return;
change(p->left, last);
if (last)
last->right = p;
p->left = last;
last = p;
change(p->right, last);
}
void main()
{
Node *root = create();
Node *tail = NULL;
change(root, tail);
while (tail)
{
cout << tail->data << " ";
tail = tail->left;
}
cout << endl;
}
--------------------------------------------------
#include <iostream>
using namespace std;
class Node{
public:
int data;
Node *left;
Node *right;
Node(int d = 0, Node *lr = 0, Node *rr = 0):data(d), left(lr), right(rr){}
};
Node *create()
{
Node *root;
Node *p4 = new Node(4);
Node *p8 = new Node(8);
Node *p6 = new Node(6, p4, p8);
Node *p12 = new Node(12);
Node *p16 = new Node(16);
Node *p14 = new Node(14, p12, p16);
Node *p10 = new Node(10, p6, p14);
root = p10;
return root;
}
Node *change(Node *p, bool asRight)
{
if (!p)
return NULL;
Node *pLeft = change(p->left, false);
if (pLeft)
pLeft->right = p;
p->left = pLeft;
Node *pRight = change(p->right, true);
if (pRight)
pRight->left = p;
p->right = pRight;
Node *r = p;
if (asRight)
{
while (r->left)
r = r->left;
}else{
while (r->right)
r = r->right;
}
return r;
}
void main(){
Node *root = create();
Node *tail = change(root, false);
while (tail)
{
cout << tail->data << " ";
tail = tail->left;
}
cout << endl;
root = create();
Node *head = change(root, true);
while (head)
{
cout << head->data << " ";
head = head->right;
}
cout << endl;
}
2.设计包含min函数的栈。
定义栈的数据结构,要求添加一个min函数,能够得到栈的最小元素。
要求函数min、push以及pop的时间复杂度都是O(1)。
结合链表一起做。
首先我做插入以下数字:10,7,3,3,8,5,2, 6
0: 10 -> NULL (MIN=10, POS=0)
1: 7 -> [0] (MIN=7, POS=1) 用数组表示堆栈,第0个元素表示栈底
2: 3 -> [1] (MIN=3, POS=2)
3: 3 -> [2] (MIN=3, POS=3)
4: 8 -> NULL (MIN=3, POS=3) 技巧在这里,因为8比当前的MIN大,所以弹出8不会对当前的MIN产生影响
5:5 -> NULL (MIN=3, POS=3)
6: 2 -> [2] (MIN=2, POS=6) 如果2出栈了,那么3就是MIN
7: 6 -> [6]
出栈的话采用类似方法修正。
所以,此题的第1小题,即是借助辅助栈,保存最小值,
且随时更新辅助栈中的元素。
如先后,push 2 6 4 1 5
stack A stack B(辅助栈)
4: 5 1 //push 5,min=p->[3]=1 ^
3: 1 1 //push 1,min=p->[3]=1 | //此刻push进A的元素1小于B中栈顶元素2
2: 4 2 //push 4,min=p->[0]=2 |
1: 6 2 //push 6,min=p->[0]=2 |
0: 2 2 //push 2,min=p->[0]=2 |
push第一个元素进A,也把它push进B,
当向Apush的元素比B中的元素小, 则也push进B,即更新B。否则,不动B,保存原值。
向栈A push元素时,顺序由下至上。
辅助栈B中,始终保存着最小的元素。
然后,pop栈A中元素,5 1 4 6 2
A B ->更新
4: 5 1 1 //pop 5,min=p->[3]=1 |
3: 1 1 2 //pop 1,min=p->[0]=2 |
2: 4 2 2 //pop 4,min=p->[0]=2 |
1: 6 2 2 //pop 6,min=p->[0]=2 |
0: 2 2 NULL //pop 2,min=NULL v
当pop A中的元素小于B中栈顶元素时,则也要pop B中栈顶元素。
---------------------------------------------------
template<typename T>
class StackSuppliedMin{
public:
vector<T> datas;
vector<size_t> minStack;
void push(T data){
datas.push_back(data);
if (minStack.empty() || data < datas[minStack.back()])
minStack.push_back(datas.size()-1);
}
void pop(){
assert(!datas.empty());
if (datas.back() == datas[minStack.back()])
minStack.pop_back();
datas.pop_back();
}
T min(){
assert(!datas.empty() && !minStack.empty());
return datas[minStack.back()];
}
void display();
};
3.求子数组的最大和
题目:
输入一个整形数组,数组里有正数也有负数。
数组中连续的一个或多个整数组成一个子数组,每个子数组都有一个和。
求所有子数组的和的最大值。要求时间复杂度为O(n)。
例如输入的数组为1, -2, 3, 10, -4, 7, 2, -5,和最大的子数组为3, 10, -4, 7, 2,
因此输出为该子数组的和18。
//July 2010/10/18
#include <iostream.h>
int maxSum(int* a, int n)
{
int sum=0;
int b=0;
for(int i=0; i<n; i++)
{
if(b<0)
b=a[i];
else
b+=a[i];
if(sum<b)
sum=b;
}
return sum;
}
int main()
{
int a[10]={1,-8,6,3,-1,5,7,-2,0,1};
cout<<maxSum(a,10)<<endl;
return 0;
}
运行结果,如下:
20
Press any key to continue
------------------------------------------------------------
int maxSum(int* a, int n)
{
int sum=0;
int b=0;
for(int i=0; i<n; i++)
{
if(b<=0) //此处修正下,把b<0改为 b<=0
b=a[i];
else
b+=a[i];
if(sum<b)
sum=b;
}
return sum;
}
//
解释下:
例如输入的数组为1, -2, 3, 10, -4, 7, 2, -5,
那么最大的子数组为3, 10, -4, 7, 2,
因此输出为该子数组的和18
所有的东西都在以下俩行,
即:
b : 0 1 -1 3 13 9 16 18 7
sum: 0 1 1 3 13 13 16 18 18
其实算法很简单,当前面的几个数,加起来后,b<0后,
把b重新赋值,置为下一个元素,b=a[i]。
当b>sum,则更新sum=b;
若b<sum,则sum保持原值,不更新。:)。July、10/31。
///
第4题,
当访问到某一结点时,把该结点添加到路径上,并累加当前结点的值。
如果当前结点为叶结点并且当前路径的和刚好等于输入的整数,则当前的路径符合要求,我们把它打印出来
。
如果当前结点不是叶结点,则继续访问它的子结点。当前结点访问结束后,递归函数将自动回到父结点。
因此我们在函数退出之前要在路径上删除当前结点并减去当前结点的值,
以确保返回父结点时路径刚好是根结点到父结点的路径。
我们不难看出保存路径的数据结构实际上是一个栈结构,因为路径要与递归调用状态一致,
而递归调用本质就是一个压栈和出栈的过程。
void FindPath
(
BinaryTreeNode* pTreeNode, // a node of binary tree
int expectedSum, // the expected sum
std::vector<int>& path, // a path from root to current node
int& currentSum // the sum of path
)
{
if(!pTreeNode)
return;
currentSum += pTreeNode->m_nValue;
path.push_back(pTreeNode->m_nValue);
// if the node is a leaf, and the sum is same as pre-defined,
// the path is what we want. print the path
bool isLeaf = (!pTreeNode->m_pLeft && !pTreeNode->m_pRight);
if(currentSum == expectedSum && isLeaf)
{
std::vector<int>::iterator iter = path.begin();
for(; iter != path.end(); ++ iter)
std::cout << *iter << '/t';
std::cout << std::endl;
}
// if the node is not a leaf, goto its children
if(pTreeNode->m_pLeft)
FindPath(pTreeNode->m_pLeft, expectedSum, path, currentSum);
if(pTreeNode->m_pRight)
FindPath(pTreeNode->m_pRight, expectedSum, path, currentSum);
// when we finish visiting a node and return to its parent node,
// we should delete this node from the path and
// minus the node's value from the current sum
currentSum -= pTreeNode->m_nValue;
path.pop_back();
}
5.查找最小的k个元素
题目:输入n个整数,输出其中最小的k个。
例如输入1,2,3,4,5,6,7和8这8个数字,
则最小的4个数字为1,2,3和4。
//July 2010/10/18
//引用自116 楼 wocaoqwer 的回复。
#include<iostream>
using namespace std;
class MinK{
public:
MinK(int *arr,int si):array(arr),size(si){}
bool kmin(int k,int*& ret){
if(k>size)
{
ret=NULL;
return false;
}
else
{
ret=new int[k--];
int i;
for(i=0;i<=k;++i)
ret[i]=array[i];
for(int j=(k-1)/2;j>=0;--j)
shiftDown(ret,j,k);
for(;i<size;++i)
if(array[i]<ret[0])
{
ret[0]=array[i];
shiftDown(ret,0,k);
}
return true;
}
}
void remove(int*& ret){
delete[] ret;
ret=NULL;
}
private:
void shiftDown(int *ret,int pos,int length){
int t=ret[pos];
for(int s=2*pos+1;s<=length;s=2*s+1){
if(s<length&&ret[s]<ret[s+1])
++s;
if(t<ret[s])
{
ret[pos]=ret[s];
pos=s;
}
else break;
}
ret[pos]=t;
}
int *array;
int size;
};
int main()
{
int array[]={1,2,3,4,5,6,7,8};
MinK mink(array,sizeof(array)/sizeof(array[0]));
int *ret;
int k=4;
if(mink.kmin(k,ret))
{
for(int i=0;i<k;++i)
cout<<ret[i]<<endl;
mink.remove(ret);
}
return 0;
}
/
运行结果:
4
2
3
1
Press any key to continue
/
---------------------
第5题,更多,请看:
程序员面试题狂想曲:第三章、寻找最小的k个数、updated 10次。
第6题
------------------------------------
腾讯面试题:
给你10分钟时间,根据上排给出十个数,在其下排填出对应的十个数
要求下排每个数都是先前上排那十个数在下排出现的次数。
上排的十个数如下:
【0,1,2,3,4,5,6,7,8,9】
初看此题,貌似很难,10分钟过去了,可能有的人,题目都还没看懂。
举一个例子,
数值: 0,1,2,3,4,5,6,7,8,9
分配: 6,2,1,0,0,0,1,0,0,0
0在下排出现了6次,1在下排出现了2次,
2在下排出现了1次,3在下排出现了0次....
以此类推..
// 引用自July 2010年10月18日。
//数值: 0,1,2,3,4,5,6,7,8,9
//分配: 6,2,1,0,0,0,1,0,0,0
#include <iostream.h>
#define len 10
class NumberTB
{
private:
int top[len];
int bottom[len];
bool success;
public:
NumberTB();
int* getBottom();
void setNextBottom();
int getFrequecy(int num);
};
NumberTB::NumberTB()
{
success = false;
//format top
for(int i=0;i<len;i++)
{
top[i] = i;
}
}
int* NumberTB::getBottom()
{
int i = 0;
while(!success)
{
i++;
setNextBottom();
}
return bottom;
}
//set next bottom
void NumberTB::setNextBottom()
{
bool reB = true;
for(int i=0;i<len;i++)
{
int frequecy = getFrequecy(i);
if(bottom[i] != frequecy)
{
bottom[i] = frequecy;
reB = false;
}
}
success = reB;
}
//get frequency in bottom
int NumberTB::getFrequecy(int num) //此处的num即指上排的数 i
{
int count = 0;
for(int i=0;i<len;i++)
{
if(bottom[i] == num)
count++;
}
return count; //cout即对应 frequecy
}
int main()
{
NumberTB nTB;
int* result= nTB.getBottom();
for(int i=0;i<len;i++)
{
cout<<*result++<<endl;
}
return 0;
}
///
运行结果:
6
2
1
0
0
0
1
0
0
0
Press any key to continue
/
第7题
------------------------------------
微软亚院之编程判断俩个链表是否相交
给出俩个单向链表的头指针,比如h1,h2,判断这俩个链表是否相交。
为了简化问题,我们假设俩个链表均不带环。
问题扩展:
1.如果链表可能有环列?
2.如果需要求出俩个链表相交的第一个节点列?
//这一题,自己也和不少人讨论过了,
//更详细的,请看这里:
//My sina Blog:
//http://blog.sina.com.cn/s/blog_5e3ab00c0100le4s.html
1.首先假定链表不带环
那么,我们只要判断俩个链表的尾指针是否相等。
相等,则链表相交;否则,链表不相交。
2.如果链表带环,
那判断一链表上俩指针相遇的那个节点,在不在另一条链表上。
如果在,则相交,如果不在,则不相交。
所以,事实上,这个问题就转化成了:
1.先判断带不带环
2.如果都不带环,就判断尾节点是否相等
3.如果都带环,判断一链表上俩指针相遇的那个节点,在不在另一条链表上。
如果在,则相交,如果不在,则不相交。
//用两个指针,一个指针步长为1,一个指针步长为2,判断链表是否有环
bool check(const node* head)
{
if(head==NULL)
return false;
node *low=head, *fast=head->next;
while(fast!=NULL && fast->next!=NULL)
{
low=low->next;
fast=fast->next->next;
if(low==fast) return true;
}
return false;
}
//如果链表可能有环,则如何判断两个链表是否相交
//思路:链表1 步长为1,链表2步长为2 ,如果有环且相交则肯定相遇,否则不相交
list1 head: p1
list2 head: p2
while( p1 != p2 && p1 != NULL && p2 != NULL )
[b]//但当链表有环但不相交时,此处是死循环。![/b]
{
p1 = p1->next;
if ( p2->next )
p2 = p2->next->next;
else
p2 = p2->next;
}
if ( p1 == p2 && p1 && p2)
//相交
else
//不相交
所以,判断带环的链表,相不相交,只能这样:
如果都带环,判断一链表上俩指针相遇的那个节点,在不在另一条链表上。
如果在,则相交,如果不在,则不相交。(未写代码实现,见谅。:)..
------------------
第9题
-----------------------------------
判断整数序列是不是二元查找树的后序遍历结果
题目:输入一个整数数组,判断该数组是不是某二元查找树的后序遍历的结果。
如果是返回true,否则返回false。
例如输入5、7、6、9、11、10、8,由于这一整数序列是如下树的后序遍历结果:
8
/ /
6 10
/ / / /
5 7 9 11
因此返回true。
如果输入7、4、6、5,没有哪棵树的后序遍历的结果是这个序列,因此返回false。
//貌似,少有人关注此题。:).2010/10/18
bool verifySquenceOfBST(int squence[], int length)
{
if(squence == NULL || length <= 0)
return false;
// root of a BST is at the end of post order traversal squence
int root = squence[length - 1];
// the nodes in left sub-tree are less than the root
int i = 0;
for(; i < length - 1; ++ i)
{
if(squence[i] > root)
break;
}
// the nodes in the right sub-tree are greater than the root
int j = i;
for(; j < length - 1; ++ j)
{
if(squence[j] < root)
return false;
}
// verify whether the left sub-tree is a BST
bool left = true;
if(i > 0)
left = verifySquenceOfBST(squence, i);
// verify whether the right sub-tree is a BST
bool right = true;
if(i < length - 1)
right = verifySquenceOfBST(squence + i, length - i - 1);
return (left && right);
}
关于第9题:
其实,就是一个后序遍历二叉树的算法。
关键点:
1.
//确定根结点
int root = squence[length - 1];
2.
// the nodes in left sub-tree are less than the root
int i = 0;
for(; i < length - 1; ++ i)
{
if(squence[i] > root)
break;
}
// the nodes in the right sub-tree are greater than the root
int j = i;
for(; j < length - 1; ++ j)
{
if(squence[j] < root)
return false;
}
3.
递归遍历,左右子树。
---------------------------------------
第10题,单词翻转。
//单词翻转,引用自117 楼 wocaoqwer 的回复。
#include<iostream>
#include<string>
using namespace std;
class ReverseWords{
public:
ReverseWords(string* wo):words(wo){}
void reverse_()
{
int length=words->size();
int begin=-1,end=-1;
for(int i=0;i<length;++i){
if(begin==-1&&words->at(i)==' ')
continue;
if(begin==-1)
{
begin=i;
continue;
}
if(words->at(i)==' ')
end=i-1;
else if(i==length-1)
end=i;
else
continue;
reverse__(begin,end); //1.字母翻转
begin=-1,end=-1;
}
reverse__(0,length-1); //2.单词翻转
}
private:
void reverse__(int begin,int end) //
{
while(begin<end)
{
char t=words->at(begin);
words->at(begin)=words->at(end);
words->at(end)=t;
++begin;
--end;
}
}
string* words;
};
int main(){
string s="I am a student.";
ReverseWords r(&s);
r.reverse_();
cout<<s<<endl;
return 0;
}
运行结果:
student. a am I
Press any key to continue
第11题
------------------------------------
求二叉树中节点的最大距离...
如果我们把二叉树看成一个图,
父子节点之间的连线看成是双向的,
我们姑且定义"距离"为两节点之间边的个数。
写一个程序,
求一棵二叉树中相距最远的两个节点之间的距离。
//July 2010/10/19
//此题思路,tree_star and i 在257、258楼,讲的很明白了。
//定义一个结构体
struct NODE
{
NODE* pLeft;
NODE* pRight;
int MaxLen;
int MaxRgt;
};
NODE* pRoot; //根节点
int MaxLength;
void traversal_MaxLen(NODE* pRoot)
{
if(pRoot == NULL)
{
return 0;
};
if(pRoot->pLeft == NULL)
{
pRoot->MaxLeft = 0;
}
else //若左子树不为空
{
int TempLen = 0;
if(pRoot->pLeft->MaxLeft > pRoot->pLeft->MaxRight)
//左子树上的,某一节点,往左边大,还是往右边大
{
TempLen+=pRoot->pLeft->MaxLeft;
}
else
{
TempLen+=pRoot->pLeft->MaxRight;
}
pRoot->nMaxLeft = TempLen + 1;
traversal_MaxLen(NODE* pRoot->pLeft);
//此处,加上递归
}
if(pRoot->pRigth == NULL)
{
pRoot->MaxRight = 0;
}
else //若右子树不为空
{
int TempLen = 0;
if(pRoot->pRight->MaxLeft > pRoot->pRight->MaxRight)
//右子树上的,某一节点,往左边大,还是往右边大
{
TempLen+=pRoot->pRight->MaxLeft;
}
else
{
TempLen+=pRoot->pRight->MaxRight;
}
pRoot->MaxRight = TempLen + 1;
traversal_MaxLen(NODE* pRoot->pRight);
//此处,加上递归
}
if(pRoot->MaxLeft + pRoot->MaxRight > 0)
{
MaxLength=pRoot->nMaxLeft + pRoot->MaxRight;
}
}
// 数据结构定义
struct NODE
{
NODE* pLeft; // 左子树
NODE* pRight; // 右子树
int nMaxLeft; // 左子树中的最长距离
int nMaxRight; // 右子树中的最长距离
char chValue; // 该节点的值
};
int nMaxLen = 0;
// 寻找树中最长的两段距离
void FindMaxLen(NODE* pRoot)
{
// 遍历到叶子节点,返回
if(pRoot == NULL)
{
return;
}
// 如果左子树为空,那么该节点的左边最长距离为0
if(pRoot -> pLeft == NULL)
{
pRoot -> nMaxLeft = 0;
}
// 如果右子树为空,那么该节点的右边最长距离为0
if(pRoot -> pRight == NULL)
{
pRoot -> nMaxRight = 0;
}
// 如果左子树不为空,递归寻找左子树最长距离
if(pRoot -> pLeft != NULL)
{
FindMaxLen(pRoot -> pLeft);
}
// 如果右子树不为空,递归寻找右子树最长距离
if(pRoot -> pRight != NULL)
{
FindMaxLen(pRoot -> pRight);
}
// 计算左子树最长节点距离
if(pRoot -> pLeft != NULL)
{
int nTempMax = 0;
if(pRoot -> pLeft -> nMaxLeft > pRoot -> pLeft -> nMaxRight)
{
nTempMax = pRoot -> pLeft -> nMaxLeft;
}
else
{
nTempMax = pRoot -> pLeft -> nMaxRight;
}
pRoot -> nMaxLeft = nTempMax + 1;
}
// 计算右子树最长节点距离
if(pRoot -> pRight != NULL)
{
int nTempMax = 0;
if(pRoot -> pRight -> nMaxLeft > pRoot -> pRight -> nMaxRight)
{
nTempMax = pRoot -> pRight -> nMaxLeft;
}
else
{
nTempMax = pRoot -> pRight -> nMaxRight;
}
pRoot -> nMaxRight = nTempMax + 1;
}
// 更新最长距离
if(pRoot -> nMaxLeft + pRoot -> nMaxRight > nMaxLen)
{
nMaxLen = pRoot -> nMaxLeft + pRoot -> nMaxRight;
}
}
//很明显,思路完全一样,但书上给的这段代码更规范!:)。
第12题
题目:求1+2+…+n,
要求不能使用乘除法、for、while、if、else、switch、case等关键字
以及条件判断语句(A?B:C)。
//July、2010/10/19
-----------------
循环只是让相同的代码执行n遍而已,我们完全可以不用for和while达到这个效果。
比如定义一个类,我们new一含有n个这种类型元素的数组,
那么该类的构造函数将确定会被调用n次。我们可以将需要执行的代码放到构造函数里。
------------------
#include <iostream.h>
class Temp
{
public:
Temp()
{
++N;
Sum += N;
}
static void Reset() { N = 0; Sum = 0; }
static int GetSum() { return Sum; }
private:
static int N;
static int Sum;
};
int Temp::N = 0;
int Temp::Sum = 0;
int solution1_Sum(int n)
{
Temp::Reset();
Temp *a = new Temp[n]; //就是这个意思,new出n个数组。
delete []a;
a = 0;
return Temp::GetSum();
}
int main()
{
cout<<solution1_Sum(100)<<endl;
return 0;
}
//运行结果:
//5050
//Press any key to continue
//July、2010/10/19
//第二种思路:
----------------
既然不能判断是不是应该终止递归,我们不妨定义两个函数。
一个函数充当递归函数的角色,另一个函数处理终止递归的情况,
我们需要做的就是在两个函数里二选一。
从二选一我们很自然的想到布尔变量,
比如ture/(1)的时候调用第一个函数,false/(0)的时候调用第二个函数。
那现在的问题是如和把数值变量n转换成布尔值。
如果对n连续做两次反运算,即!!n,那么非零的n转换为true,0转换为false。
#include <iostream.h>
class A;
A* Array[2];
class A
{
public:
virtual int Sum (int n) { return 0; }
};
class B: public A
{
public:
virtual int Sum (int n) { return Array[!!n]->Sum(n-1)+n; }
};
int solution2_Sum(int n)
{
A a;
B b;
Array[0] = &a;
Array[1] = &b;
int value = Array[1]->Sum(n);
//利用虚函数的特性,当Array[1]为0时,即Array[0] = &a; 执行A::Sum,
//当Array[1]不为0时, 即Array[1] = &b; 执行B::Sum。
return value;
}
int main()
{
cout<<solution2_Sum(100)<<endl;
return 0;
}
//5050
//Press any key to continue
第13题:
题目:
输入一个单向链表,输出该链表中倒数第k个结点,
链表的倒数第0个结点为链表的尾指针。
//此题一出,相信,稍微有点 经验的同志,都会说到:
------------------------
设置两个指针p1,p2
首先p1和p2都指向head
然后p2向前走n步,这样p1和p2之间就间隔k个节点
然后p1和p2同……
#include <iostream.h>
#include <stdio.h>
#include <stdlib.h>
struct ListNode
{
char data;
ListNode* next;
};
ListNode* head,*p,*q;
ListNode *pone,*ptwo;
ListNode* fun(ListNode *head,int k)
{
pone = ptwo = head;
for(int i=0;i<=k-1;i++)
ptwo=ptwo->next;
while(ptwo!=NULL)
{
pone=pone->next;
ptwo=ptwo->next;
}
return pone;
}
int main()
{
char c;
head = (ListNode*)malloc(sizeof(ListNode));
head->next = NULL;
p = head;
while(c !='0')
{
q = (ListNode*)malloc(sizeof(ListNode));
q->data = c;
q->next = NULL;
p->next = q;
p = p->next;
c = getchar();
}
cout<<"---------------"<<endl;
cout<<fun(head,2)->data<<endl;
return 0;
}
/
1254863210
---------------
2
Press any key to continue
第14题:
题目:输入一个已经按升序排序过的数组和一个数字,
在数组中查找两个数,使得它们的和正好是输入的那个数字。
要求时间复杂度是O(n)。
如果有多对数字的和等于输入的数字,输出任意一对即可。
例如输入数组1、2、4、7、11、15和数字15。由于4+11=15,因此输出4和11。
//由于数组已经过升序排列,所以,难度下降了不少。
//July、2010/10/19
#include <iostream.h>
bool FindTwoNumbersWithSum
(
int data[], // 已经排序的 数组
unsigned int length, // 数组长度
int sum, //用户输入的 sum
int& num1, // 输出符合和等于sum的第一个数
int& num2 // 第二个数
)
{
bool found = false;
if(length < 1)
return found;
int begin = 0;
int end = length - 1;
while(end > begin)
{
long curSum = data[begin] + data[end];
if(curSum == sum)
{
num1 = data[begin];
num2 = data[end];
found = true;
break;
}
else if(curSum > sum)
end--;
else
begin++;
}
return found;
}
int main()
{
int x,y;
int a[6]={1,2,4,7,11,15};
if(FindTwoNumbersWithSum(a,6,15,x,y) )
{
cout<<x<<endl<<y<<endl;
}
return 0;
}
4
11
Press any key to continue
扩展:如果输入的数组是没有排序的,但知道里面数字的范围,其他条件不变,
如何在O(n)时间里找到这两个数字?
关于第14题,
1.题目假定是,只要找出俩个数,的和等于给定的数,
其实是,当给定一排数,
4,5,7,10,12
然后给定一个数,22。
就有俩种可能了。因为22=10+12=10+5+7。
而恰恰与第4题,有关联了。望大家继续思考下。:)。
2.第14题,还有一种思路,如下俩个数组:
1、 2、 4、7、11、15 //用15减一下为
14、13、11、8、4、 0 //如果下面出现了和上面一样的数,稍加判断,就能找出这俩个数来了。
第一个数组向右扫描,第二个数组向左扫描。
第15题:
题目:输入一颗二元查找树,将该树转换为它的镜像,
即在转换后的二元查找树中,左子树的结点都大于右子树的结点。
用递归和循环两种方法完成树的镜像转换。
例如输入:
8
/ /
6 10
/ / / /
5 7 9 11
输出:
8
/ /
10 6
/ / / /
11 9 7 5
定义二元查找树的结点为:
struct BSTreeNode // a node in the binary search tree (BST)
{
int m_nValue; // value of node
BSTreeNode *m_pLeft; // left child of node
BSTreeNode *m_pRight; // right child of node
};
//就是递归翻转树,有子树则递归翻转子树。
//July、2010/10/19
void Revertsetree(list *root)
{
if(!root)
return;
list *p;
p=root->leftch;
root->leftch=root->rightch;
root->rightch=p;
if(root->leftch)
Revertsetree(root->leftch);
if(root->rightch)
Revertsetree(root->rightch);
}
由于递归的本质是编译器生成了一个函数调用的栈,
因此用循环来完成同样任务时最简单的办法就是用一个辅助栈来模拟递归。
首先我们把树的头结点放入栈中。
在循环中,只要栈不为空,弹出栈的栈顶结点,交换它的左右子树。
如果它有左子树,把它的左子树压入栈中;
如果它有右子树,把它的右子树压入栈中。
这样在下次循环中就能交换它儿子结点的左右子树了。
//再用辅助栈模拟递归,改成循环的(有误之处,望不吝指正):
void Revertsetree(list *phead)
{
if(!phead)
return;
stack<list*> stacklist;
stacklist.push(phead); //首先把树的头结点放入栈中。
while(stacklist.size())
//在循环中,只要栈不为空,弹出栈的栈顶结点,交换它的左右子树
{
list* pnode=stacklist.top();
stacklist.pop();
list *ptemp;
ptemp=pnode->leftch;
pnode->leftch=pnode->rightch;
pnode->rightch=ptemp;
if(pnode->leftch)
stacklist.push(pnode->leftch); //若有左子树,把它的左子树压入栈中
if(pnode->rightch)
stacklist.push(pnode->rightch); //若有右子树,把它的右子树压入栈中
}
}
第16题
题目:输入一颗二元树,从上往下按层打印树的每个结点,同一层中按照从左往右的顺序打印。
例如输入
8
/ /
6 10
// //
5 7 9 11
输出8 6 10 5 7 9 11。
//题目不是我们所熟悉的,树的前序,中序,后序。即是树的层次遍历。
/*308 楼 panda_lin 的回复,说的已经很好了。:)
利用队列,每个单元对应二叉树的一个节点.
1:输出8, 队列内容: 6, 10
2:输出6, 6的2个子节点5,7入队列。队列的内容:10, 5, 7
3:输出10,10的2个子节点9,11入队列。队列的内容:5,7,9,11。
4:输出5 ,5没有子节点。队列的内容:7,9,11
5:。。。
由于STL已经为我们实现了一个很好的deque(两端都可以进出的队列),
我们只需要拿过来用就可以了。
我们知道树是图的一种特殊退化形式。
同时如果对图的深度优先遍历和广度优先遍历有比较深刻的理解,
将不难看出这种遍历方式实际上是一种广度优先遍历。
因此这道题的本质是在二元树上实现广度优先遍历。
//July、2010/10/19/晚。
#include <deque>
#include <iostream>
using namespace std;
struct BTreeNode // a node in the binary tree
{
int m_nValue; // value of node
BTreeNode *m_pLeft; // left child of node
BTreeNode *m_pRight; // right child of node
};
BTreeNode* pListIndex;
BTreeNode* pHead;
void PrintFromTopToBottom(BTreeNode *pTreeRoot)
{
if(!pTreeRoot)
return;
// get a empty queue
deque<BTreeNode *> dequeTreeNode;
// insert the root at the tail of queue
dequeTreeNode.push_back(pTreeRoot);
while(dequeTreeNode.size())
{
// get a node from the head of queue
BTreeNode *pNode = dequeTreeNode.front();
dequeTreeNode.pop_front();
// print the node
cout << pNode->m_nValue << ' ';
// print its left child sub-tree if it has
if(pNode->m_pLeft)
dequeTreeNode.push_back(pNode->m_pLeft);
// print its right child sub-tree if it has
if(pNode->m_pRight)
dequeTreeNode.push_back(pNode->m_pRight);
}
}
// 创建二元查找树
void addBTreeNode(BTreeNode * & pCurrent, int value)
{
if (NULL == pCurrent)
{
BTreeNode * pBTree = new BTreeNode();
pBTree->m_pLeft = NULL;
pBTree->m_pRight = NULL;
pBTree->m_nValue = value;
pCurrent = pBTree;
}
else
{
if ((pCurrent->m_nValue) > value)
{
addBTreeNode(pCurrent->m_pLeft, value);
}
else if ((pCurrent->m_nValue) < value)
{
addBTreeNode(pCurrent->m_pRight, value);
}
}
}
int main()
{
BTreeNode * pRoot = NULL;
pListIndex = NULL;
pHead = NULL;
addBTreeNode(pRoot, 8);
addBTreeNode(pRoot, 6);
addBTreeNode(pRoot, 5);
addBTreeNode(pRoot, 7);
addBTreeNode(pRoot, 10);
addBTreeNode(pRoot, 9);
addBTreeNode(pRoot, 11);
PrintFromTopToBottom(pRoot);
return 0;
}
//输出结果:
//8 6 10 5 7 9 11 Press any key to continue
是的,由这道题,突然想到了,树的广度优先遍历,BFS算法。
第17题:
题目:在一个字符串中找到第一个只出现一次的字符。
如输入abaccdeff,则输出b。
这道题是2006年google的一道笔试题。
思路剖析:由于题目与字符出现的次数相关,我们可以统计每个字符在该字符串中出现的次数.
要达到这个目的,需要一个数据容器来存放每个字符的出现次数。
在这个数据容器中可以根据字符来查找它出现的次数,
也就是说这个容器的作用是把一个字符映射成一个数字。
在常用的数据容器中,哈希表正是这个用途。
由于本题的特殊性,我们只需要一个非常简单的哈希表就能满足要求。
由于字符(char)是一个长度为8的数据类型,因此总共有可能256 种可能。
于是我们创建一个长度为256的数组,每个字母根据其ASCII码值作为数组的下标对应数组的对应项,
而数组中存储的是每个字符对应的次数。
这样我们就创建了一个大小为256,以字符ASCII码为键值的哈希表。
我们第一遍扫描这个数组时,每碰到一个字符,在哈希表中找到对应的项并把出现的次数增加一次。
这样在进行第二次扫描时,就能直接从哈希表中得到每个字符出现的次数了。
//July、2010/10/20
#include <iostream.h>
#include <string.h>
char FirstNotRepeatingChar(char* pString)
{
if(!pString)
return 0;
const int tableSize = 256;
unsigned int hashTable[tableSize];
for(unsigned int i = 0; i < tableSize; ++ i)
hashTable[i] = 0;
char* pHashKey = pString;
while(*(pHashKey) != '/0')
hashTable[*(pHashKey++)] ++;
pHashKey = pString;
while(*pHashKey != '/0')
{
if(hashTable[*pHashKey] == 1)
return *pHashKey;
pHashKey++;
}
return *pHashKey;
}
int main()
{
cout<<"请输入一串字符:"<<endl;
char s[100];
cin>>s;
char* ps=s;
cout<<FirstNotRepeatingChar(ps)<<endl;
return 0;
}
//
请输入一串字符:
abaccdeff
b
Press any key to continue
///
第18题:
题目:n个数字(0,1,…,n-1)形成一个圆圈,从数字0开始,
每次从这个圆圈中删除第m个数字(第一个为当前数字本身,第二个为当前数字的下一个数字)。
当一个数字删除后,从被删除数字的下一个继续删除第m个数字。
求出在这个圆圈中剩下的最后一个数字。
July:我想,这个题目,不少人已经 见识过了。
先看这个题目的简单变形。
n个人围成一圈,顺序排号。从第一个人开始报数(从1到3报数),
凡报到3的人退出圈子,问最后留下的是原来第几号的那个人?
---------------------------------------------------------
//July、2010/10/20
//我把这100题,当每日必须完成的作业,来做了。:)。
#include <stdio.h>
int main()
{
int i,k,m,n,num[50],*p;
printf("input number of person:n=");
scanf("%d",&n);
printf("input number of the quit:m="); //留下->18题
scanf("%d",&m); //留下->18题
p=num;
for(i=0;i<n;i++)
*(p+i)=i+1; //给每个人编号
i=0; //报数
k=0; //此处为3
// m=0; //m为退出人数 //去掉->18题
while(m<n-1)
{
if(*(p+i)!=0)
k++;
if(k==3)
{
*(p+i)=0; //退出,对应的数组元素置为0
k=0;
m++;
}
i++;
if(i==n)
i=0;
}
while(*p==0)
p++;
printf("The last one is NO.%d/n",*p);
}
//
int LastRemaining_Solution2(int n, unsigned int m)
{
// invalid input
if(n <= 0 || m < 0)
return -1;
// if there are only one integer in the circle initially,
// of course the last remaining one is 0
int lastinteger = 0;
// find the last remaining one in the circle with n integers
for (int i = 2; i <= n; i ++)
lastinteger = (lastinteger + m) % i;
return lastinteger;
}
第19题:
题目:定义Fibonacci数列如下:
/ 0 n=0
f(n)= 1 n=1,2
/ f(n-1)+f(n-2) n>2
输入n,用最快的方法求该数列的第n项。
分析:在很多C语言教科书中讲到递归函数的时候,都会用Fibonacci作为例子。
因此很多程序员对这道题的递归解法非常熟悉,但....呵呵,你知道的。。
//0 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597..........
//注意,当求第100项,甚至更大的项时,请确保你用什么类型,长整型?or long long int存储。
//不然,计算机,将 得不到结果。
//若用递归方法,可写 下如下代码:
#include <iostream.h>
int Fibona(int n)
{
int m;
if(n==0)
return 0;
else if(n==1||n==2)
return 1;
else
{
m=Fibona(n-1)+Fibona(n-2);
return m;
}
}
int main()
{
cout<<"-----------------"<<endl;
cout<<Fibona(17)<<endl;
return 0;
}
---------------------------
科书上反复用这个题目来讲解递归函数,并不能说明递归解法最适合这道题目。
我们以求解f(10)作为例子来分析递归求解的过程。
要求得f(10),需要求得f(9)和f(8)。同样,要求得f(9),要先求得f(8)和f(7)……
我们用树形结构来表示这种依赖关系
f(10)
/ /
f(9) f(8)
/ / / /
f(8) f(7) f(6) f(5)
/ / / /
f(7) f(6) f(6) f(5)
更简单的办法是从下往上计算,首先根据f(0)和f(1)算出f(2),再根据f(1)和f(2)算出f(3)……
依此类推就可以算出第n项了。很容易理解,这种思路的时间复杂度是O(n)。
其实,就是转化为非递归程序,用递推。!
------------------------------------------
long long Fibonacci_Solution2(unsigned n)
{
int result[2] = {0, 1};
if(n < 2)
return result[n];
long long fibNMinusOne = 1;
long long fibNMinusTwo = 0;
long long fibN = 0;
for(unsigned int i = 2; i <= n; ++ i)
{
fibN = fibNMinusOne + fibNMinusTwo;
fibNMinusTwo = fibNMinusOne;
fibNMinusOne = fibN;
}
return fibN;
}
//很可惜,这还不是最快的方法。
//还有一种方法,可达到,时间复杂度为O(lgn).
//............
第20题:
题目:输入一个表示整数的字符串,把该字符串转换成整数并输出。
例如输入字符串"345",则输出整数345。
-----------------------------
此题一点也不简单。不信,你就先不看一下的代码,
你自己先写一份,然后再对比一下,便知道了。
1.转换的思路:每扫描到一个字符,我们把在之前得到的数字乘以10再加上当前字符表示的数字。
这个思路用循环不难实现。
2.由于整数可能不仅仅之含有数字,还有可能以'+'或者'-'开头,表示整数的正负。
如果第一个字符是'+'号,则不需要做任何操作;如果第一个字符是'-'号,
则表明这个整数是个负数,在最后的时候我们要把得到的数值变成负数。
3.接着我们试着处理非法输入。由于输入的是指针,在使用指针之前,
我们要做的第一件是判断这个指针是不是为空。
如果试着去访问空指针,将不可避免地导致程序崩溃。
4.输入的字符串中可能含有不是数字的字符。
每当碰到这些非法的字符,我们就没有必要再继续转换。
最后一个需要考虑的问题是溢出问题。由于输入的数字是以字符串的形式输入,
因此有可能输入一个很大的数字转换之后会超过能够表示的最大的整数而溢出。
//July、2010、10/22。
enum Status {kValid = 0, kInvalid};
int g_nStatus = kValid;
int StrToInt(const char* str)
{
g_nStatus = kInvalid;
long long num = 0;
if(str != NULL)
{
const char* digit = str;
// the first char in the string maybe '+' or '-'
bool minus = false;
if(*digit == '+')
digit ++;
else if(*digit == '-')
{
digit ++;
minus = true;
}
// the remaining chars in the string
while(*digit != '/0')
{
if(*digit >= '0' && *digit <= '9')
{
num = num * 10 + (*digit - '0');
// overflow
if(num > std::numeric_limits<int>::max())
{
num = 0;
break;
}
digit ++;
}
// if the char is not a digit, invalid input
else
{
num = 0;
break;
}
}
if(*digit == '/0')
{
g_nStatus = kValid;
if(minus)
num = 0 - num;
}
}
return static_cast<int>(num);
}
//在C语言提供的库函数中,函数atoi能够把字符串转换整数。
//它的声明是int atoi(const char *str)。该函数就是用一个全局变量来标志输入是否合法的。
答案V0.2版完。
完整答案,请到我的资源下载处下载。
永久勘误:微软等面试100题答案V0.3版[第21-40题答案]
微软等面试100题答案V0.3版第21-40题部分答案精选
作者:July 、何海涛等网友
-------------------------------------
开诚布公,接受读者质检
本文,是根据我之前上传的,微软等面试100题,的答案V0.3版[第21-40题答案]的部分答案精选,
而写。
现在,原版答案V0.3版公布出来,接受读者检验。
此文永久勘误、永久优化。同时,希望,各位不吝指正。谢谢。
===========
本微软等100题系列V0.1版,永久维护(网友,思路回复)地址:
http://topic.csdn.net/u/20101126/10/b4f12a00-6280-492f-b785-cb6835a63dc9.html
ok。
-----------------------
第21题
2010年中兴面试题
编程求解:
输入两个整数 n 和 m,从数列1,2,3.......n 中 随意取几个数,
使其和等于 m ,要求将其中所有的可能组合列出来.
//此题与第14题差不多,在次不做过多解释。
//July、本程序,经网友指出有误,但暂时没有想到解决的办法。见谅。2010/10/22。
updated:第20题首次勘误,请参见第749、750、751楼(已经测试正确,后续将具体分析与优化):http://topic.csdn.net/u/20101126/10/b4f12a00-6280-492f-b785-cb6835a63dc9_8.html。有任何问题,欢迎任何朋友随时指出。二零一一年四月二十日,July,updated。
- // 21题递归方法
- //这个,没有任何问题
- //from yansha
- //July、updated。
- #include<list>
- #include<iostream>
- using namespace std;
- list<int>list1;
- void find_factor(int sum, int n)
- {
- // 递归出口
- if(n <= 0 || sum <= 0)
- return;
- // 输出找到的结果
- if(sum == n)
- {
- // 反转list
- list1.reverse();
- for(list<int>::iterator iter = list1.begin(); iter != list1.end(); iter++)
- cout << *iter << " + ";
- cout << n << endl;
- list1.reverse();
- }
- list1.push_front(n); //典型的01背包问题
- find_factor(sum-n, n-1); //放n,n-1个数填满sum-n
- list1.pop_front();
- find_factor(sum, n-1); //不放n,n-1个数填满sum
- }
- int main()
- {
- int sum, n;
- cout << "请输入你要等于多少的数值sum:" << endl;
- cin >> sum;
- cout << "请输入你要从1.....n数列中取值的n:" << endl;
- cin >> n;
- cout << "所有可能的序列,如下:" << endl;
- find_factor(sum,n);
- return 0;
- }
第22题:
有4张红色的牌和4张蓝色的牌,主持人先拿任意两张,
再分别在A、B、C三人额头上贴任意两张牌,
A、B、C三人都可以看见其余两人额头上的牌,
看完后让他们猜自己额头上是什么颜色的牌,
A说不知道,B说不知道,C说不知道,然后A说知道了。
请教如何推理,A是怎么知道的。如果用程序,又怎么实现呢?
//July、2010/10/22
//今是老妈生日,祝福老妈,生日快乐。!:).
4张 r 4张b
有以下3种组合:
rr bb rb
1.B,C全是一种颜色
B C A
bb.rr bb.rr
2.
B C A
bb rr bb/RR/BR,=>A:BR
rr bb =>A:BR
3.
B C A
BR BB RR/BR, =>A:BR
//推出A:BR的原因,
//如果 A是 RR,
//那么,当ABC都说不知道后,B 最后应该知道自己是BR了。
//因为B 不可能 是 RR或BB。
4.
B C A
BR BR BB/RR/BR
//推出A:BR的原因
//i、 如果,A是 BB,那么B=>BR/RR,
//如果B=>RR,那么一开始,C就该知道自己是BR了(A俩蓝,B俩红)。(如果C.A俩蓝,那么B就一开始知道,如果C.B俩红,那么A一开始就知道,所以,论证前头,当B=>RR,那么一开始,C就该知道自己是BR)。
//如果B=>BR,那么,同样道理,C一开始也该知道自己是BR了。
//ii、 如果A是RR....
//iii、最后,也还是推出=>A:BR
//至于程序,暂等高人。
第24题:反转链表
pPrev<-pNode<-pNext
ListNode* ReverseIteratively(ListNode* pHead)
{
ListNode* pReversedHead = NULL;
ListNode* pNode = pHead;
ListNode* pPrev = NULL;
while(pNode != NULL) //pNode<=>m
{
ListNode* pNext = pNode->m_pNext; //n保存在pNext下
//如果pNext指为空,则当前结点pNode设为头。
if(pNext == NULL)
pReversedHead = pNode;
// reverse the linkage between nodes
pNode->m_pNext = pPrev;
// move forward on the the list
pPrev = pNode;
pNode = pNext;
}
return pReversedHead;
}
或者,这样写:
head->next -> p-> q
template<class T>
Node<T>* Reverse(Node<T>* head)
{
p=head->next;
while(p)
{
q=p->next; //p->next先保存在q下
p->next=head->next; //p掉头指向head->next
head->next=p; //p赋给head->next
p=q; //q赋给p。
//上俩行即,指针前移嘛...
}
return head;
第25题:
写一个函数,它的原形是int continumax(char *outputstr,char *intputstr)
功能:
在字符串中找出连续最长的数字串,并把这个串的长度返回,
并把这个最长数字串付给其中一个函数参数outputstr所指内存。
例如:"abcd12345ed125ss123456789"的首地址传给intputstr后,函数将返回9,
outputstr所指的值为123456789
//leeyunce
这个相对比较简单,思路不用多说,跟在序列中求最小值差不多。未经测试。有错误欢迎指出。
int continumax(char *outputstr, char *intputstr)
{
int i, maxlen = 0;
char * maxstr = 0;
while (true)
{
while (intputstr && (*intputstr<'0' || *intputstr>'9')) //skip all non-digit
characters
{
intputstr++;
}
if (!intputstr) break;
int count = 0;
char * tempstr = intputstr;
while (intputstr && (*intputstr>='0' && *intputstr<='9')) //OK, these characters are
digits
{
count++;
intputstr++;
}
if (count > maxlen)
{
maxlen = count;
maxstr = tempstr;
}
}
for (i=0; i<maxlen; i++)
{
outputstr[i] = maxstr[i];
}
outputstr[i] = 0;
return maxlen;
}
26.左旋转字符串
题目:
定义字符串的左旋转操作:把字符串前面的若干个字符移动到字符串的尾部。
如把字符串abcdef左旋转2位得到字符串cdefab。请实现字符串左旋转的函数。
要求时间对长度为n的字符串操作的复杂度为O(n),辅助内存为O(1)。
分析:如果不考虑时间和空间复杂度的限制,
最简单的方法莫过于把这道题看成是把字符串分成前后两部分,
通过旋转操作把这两个部分交换位置。
于是我们可以新开辟一块长度为n+1的辅助空间,
把原字符串后半部分拷贝到新空间的前半部分,在把原字符串的前半部分拷贝到新空间的后半部分。
不难看出,这种思路的时间复杂度是O(n),需要的辅助空间也是O(n)。
把字符串看成有两段组成的,记位XY。左旋转相当于要把字符串XY变成YX。
我们先在字符串上定义一种翻转的操作,就是翻转字符串中字符的先后顺序。把X翻转后记为XT。显然有
(XT)T=X。
我们首先对X和Y两段分别进行翻转操作,这样就能得到XTYT。
接着再对XTYT进行翻转操作,得到(XTYT)T=(YT)T(XT)T=YX。正好是我们期待的结果。
分析到这里我们再回到原来的题目。我们要做的仅仅是把字符串分成两段,
第一段为前面m个字符,其余的字符分到第二段。
再定义一个翻转字符串的函数,按照前面的步骤翻转三次就行了。
时间复杂度和空间复杂度都合乎要求。
#include "string.h"
// Move the first n chars in a string to its end
char* LeftRotateString(char* pStr, unsigned int n)
{
if(pStr != NULL)
{
int nLength = static_cast<int>(strlen(pStr));
if(nLength > 0 || n == 0 || n > nLength)
{
char* pFirstStart = pStr;
char* pFirstEnd = pStr + n - 1;
char* pSecondStart = pStr + n;
char* pSecondEnd = pStr + nLength - 1;
// reverse the first part of the string
ReverseString(pFirstStart, pFirstEnd);
// reverse the second part of the strint
ReverseString(pSecondStart, pSecondEnd);
// reverse the whole string
ReverseString(pFirstStart, pSecondEnd);
}
}
return pStr;
}
// Reverse the string between pStart and pEnd
void ReverseString(char* pStart, char* pEnd)
{
if(pStart == NULL || pEnd == NULL)
{
while(pStart <= pEnd)
{
char temp = *pStart;
*pStart = *pEnd;
*pEnd = temp;
pStart ++;
pEnd --;
}
}
}
========================
针对262 楼 litaoye 的回复:
26.左旋转字符串
跟panda所想,是一样的,即,
以abcdef为例
1. ab->ba
2. cdef->fedc
原字符串变为bafedc
3. 整个翻转:cdefab
//时间复杂度为O(n)
在此,奉献另外一种思路:
abc defghi,要abc移动至最后
abc defghi->def abcghi->def ghiabc
一俩指针,p1指向ch[0],p2指向[ch m-1],
p2每次移动m 的距离,p1 也跟着相应移动,
每次移动过后,交换。
如上第一步,交换abc 和def ,就变成了 abcdef->defabc
第一步,
abc defghi->def abcghi
第二步,继续交换,
def abcghi->def ghiabc
整个过程,看起来,就是abc 一步一步 向后移动
abc defghi
def abcghi
def ghi abc
//最后的 复杂度是O(m+n)
再举一个例子,
如果123 4567890要变成4567890 123:
123 4567890
1. 456 123 7890
2. 456789 123 0
3. 456789 12 0 3
4. 456789 1 0 23
5. 4567890 123 //最后三步,相当于0前移,p1已经不动。
欢迎,就此第26题,继续讨论。
二零一一年一月十七日补正。
=============================================
27.跳台阶问题
题目:一个台阶总共有n级,如果一次可以跳1级,也可以跳2级。
求总共有多少总跳法,并分析算法的时间复杂度。
首先我们考虑最简单的情况。如果只有1级台阶,那显然只有一种跳法。
如果有2级台阶,那就有两种跳的方法了:一种是分两次跳,每次跳1级;另外一种就是一次跳2级。
现在我们再来讨论一般情况。我们把n级台阶时的跳法看成是n的函数,记为f(n)。
当n>2时,第一次跳的时候就有两种不同的选择:一是第一次只跳1级,
此时跳法数目等于后面剩下的n-1级台阶的跳法数目,即为f(n-1);
另外一种选择是第一次跳2级,此时跳法数目等于后面剩下的n-2级台阶的跳法数目,即为f(n-2)。
因此n级台阶时的不同跳法的总数f(n)=f(n-1)+(f-2)。
我们把上面的分析用一个公式总结如下:
/ 1 n=1
f(n)= 2 n=2
/ f(n-1)+(f-2) n>2
分析到这里,相信很多人都能看出这就是我们熟悉的Fibonacci序列。
int jump_sum(int n) //递归版本
{
assert(n>0);
if (n == 1 || n == 2) return n;
return jump_sum(n-1)+jump_sum(n-2);
}
int jump_sum(int n) //迭代版本
{
assert(n>0);
if (n == 1 || n == 2) return n;
int an, an_1=2, an_2=1;
for (; n>=3; n--)
{
an = an_2 + an_1;
an_2 = an_1;
an_1 = an;
}
return an;
}
28.整数的二进制表示中1的个数
题目:输入一个整数,求该整数的二进制表达中有多少个1。
例如输入10,由于其二进制表示为1010,有两个1,因此输出2。
分析:
这是一道很基本的考查位运算的面试题。
包括微软在内的……
一个很基本的想法是,我们先判断整数的最右边一位是不是1。
接着把整数右移一位,原来处于右边第二位的数字现在被移到第一位了,
再判断是不是1。
这样每次移动一位,直到这个整数变成0为止。
现在的问题变成怎样判断一个整数的最右边一位是不是1了。
很简单,如果它和整数1作与运算。由于1除了最右边一位以外,其他所有位都为0。
因此如果与运算的结果为1,表示整数的最右边一位是1,否则是0。*/
得到的代码如下:
///
// Get how many 1s in an integer's binary expression
///
int NumberOf1_Solution1(int i)
{
int count = 0;
while(i)
{
if(i & 1)
count ++;
i = i >> 1;
}
return count;
}
可能有读者会问,整数右移一位在数学上是和除以2是等价的。
那可不可以把上面的代码中的右移运算符换成除以2呢?答案是最好不要换成除法。
因为除法的效率比移位运算要低的多,
在实际编程中如果可以应尽可能地用移位运算符代替乘除法。
这个思路当输入i是正数时没有问题,但当输入的i是一个负数时,
不但不能得到正确的1的个数,还将导致死循环。
以负数0x80000000为例,右移一位的时候,
并不是简单地把最高位的1移到第二位变成0x40000000,
而是0xC0000000。这是因为移位前是个负数,仍然要保证移位后是个负数,
因此移位后的最高位会设为1。
如果一直做右移运算,最终这个数字就会变成0xFFFFFFFF而陷入死循环。
为了避免死循环,我们可以不右移输入的数字i。
首先i和1做与运算,判断i的最低位是不是为1。
接着把1左移一位得到2,再和i做与运算,就能判断i的次高位是不是1……
这样反复左移,每次都能判断i的其中一位是不是1。基于此,我们得到如下代码:
///
// Get how many 1s in an integer's binary expression
///
int NumberOf1_Solution2(int i)
{
int count = 0;
unsigned int flag = 1;
while(flag)
{
if(i & flag)
count ++;
flag = flag << 1;
}
return count;
}
29.栈的push、pop序列
题目:输入两个整数序列。其中一个序列表示栈的push顺序,
判断另一个序列有没有可能是对应的pop顺序。
如果我们希望pop的数字正好是栈顶数字,直接pop出栈即可;
如果希望pop的数字目前不在栈顶,我们就到
push序列中还没有被push到栈里的数字中去搜索这个数字,
并把在它之前的所有数字都push进栈。
如果所有的数字都被push进栈仍然没有找到这个数字,表明该序列不可能是一个pop序列。
我们来着重分析下此题:
push序列已经固定,
push pop
--- -- -> /---->
5 4 3 2 1 / 4 5 3 2 1
| 5 |
| 4 |
| 3 |
| 2 |
|___1__|
1.要得到4 5 3 2 1的pop序列,即pop的顺序为4->5->3->2->1
首先,要pop4,可让push5 之前,pop4,然后push5,pop5
然后发现3在栈顶,直接pop 3..2..1
2.再看一序列,
push pop
--- -- -> /---->
5 4 3 2 1 / 4 3 5 1 2
| 5 |
| 4 |
| 3 |
| 2 |
|___1__|
想得到4 3 5 1 2的pop序列,是否可能? 4->3->5->1->2
同样在push5之前,push 了 4 3 2 1,pop4,pop 3,然后再push 5,pop5
2
再看栈中的从底至上是 1 ,由于1 2已经在栈中,所以只能先pop2,才能pop1。
所以,很显然,不可能有 4 3 5 1 2的 pop序列。
所以上述那段注释的话的意思,即是,
如果,一个元素在栈顶,直接pop即可。如果它不在栈顶,那么从push序列中找这个元素
找到,那么push 它,然后再 pop 它。否则,无法在 那个顺序中 pop。
//
push序列已经固定,
push pop
--- -- -> /---->
5 4 3 2 1 / 3 5 4 2 1 //可行
| 5 | 1 4 5 3 2 //亦可行,不知各位,是否已明了题意?:)..
| 4 |
| 3 |
| 2 |
|___1__|
///
今早我也来了,呵。
昨晚,后来,自个又想了想,要怎么才能pop想要的一个数列?
push序列已经固定,
push pop
--- -- -> /---->
5 4 3 2 1 / 5 4 3 2 1
| 5 |
| 4 |
| 3 |
| 2 |
|___1__|
比如,当栈中已有数列 2
1
而现在我随机 要 pop4,一看,4不在栈中,再从push序列中,
正好,4在push队列中,push4进栈之前,还得把 4前面的数,即3 先push进来,。
好,现在,push 3, push 4,然后便是想要的结果:pop 4。
所以,当我要pop 一个数时,先看这个数 在不在已经push的 栈顶,如果,在,好,直接pop它。
如果,不在,那么,从 push序列中,去找这个数,找到后,push 它进栈,
如果push队列中它的前面还有数,那么 还得把它前面数,先push进栈。
如果铺设队列中没有这个数,那当然 就不是存在这个 pop 结果了。
不知,我说明白了没?:).接下来,给一段,参考程序:
//有误之处,恳请指正。July、2010/11/09。:)。
bool IsPossiblePopOrder(const int* pPush, const int* pPop, int nLength)
{
bool bPossible = false;
if(pPush && pPop && nLength > 0)
{
const int *pNextPush = pPush;
const int *pNextPop = pPop;
// ancillary stack
std::stack<int> stackData;
// check every integers in pPop
while(pNextPop - pPop < nLength)
{
// while the top of the ancillary stack is not the integer
// to be poped, try to push some integers into the stack
while(stackData.empty() || stackData.top() != *pNextPop)
{
// pNextPush == NULL means all integers have been
// pushed into the stack, can't push any longer
if(!pNextPush)
break;
stackData.push(*pNextPush);
// if there are integers left in pPush, move
// pNextPush forward, otherwise set it to be NULL
if(pNextPush - pPush < nLength - 1)
pNextPush ++;
else
pNextPush = NULL;
}
// After pushing, the top of stack is still not same as
// pPextPop, pPextPop is not in a pop sequence
// corresponding to pPush
if(stackData.top() != *pNextPop)
break;
// Check the next integer in pPop
stackData.pop();
pNextPop ++;
}
// if all integers in pPop have been check successfully,
// pPop is a pop sequence corresponding to pPush
if(stackData.empty() && pNextPop - pPop == nLength)
bPossible = true;
}
return bPossible;
}
30.在从1到n的正数中1出现的次数
题目:输入一个整数n,求从1到n这n个整数的十进制表示中1出现的次数。
例如输入12,从1到12这些整数中包含1 的数字有1,10,11和12,1一共出现了5次。
分析:这是一道广为流传的google面试题。
我们每次判断整数的个位数字是不是1。如果这个数字大于10,除以10之后再判断个位数字是不是1。
基于这个思路,不难写出如下的代码:*/
int NumberOf1(unsigned int n);
int NumberOf1BeforeBetween1AndN_Solution1(unsigned int n)
{
int number = 0;
// Find the number of 1 in each integer between 1 and n
for(unsigned int i = 1; i <= n; ++ i)
number += NumberOf1(i);
return number;
}
int NumberOf1(unsigned int n)
{
int number = 0;
while(n)
{
if(n % 10 == 1)
number ++;
n = n / 10;
}
return number;
}
这个思路有一个非常明显的缺点就是每个数字都要计算1在该数字中出现的次数,因此时间复杂度是O(n)。
当输入的n非常大的时候,需要大量的计算,运算效率很低。
各位,不妨讨论下,更好的解决办法。:)...
---------------------------
第30题,网友love8909给的思路:
char num[16];
int len, dp[16][16][2];
int dfs(int pos, int ct, int less)
{
if (pos == len)
return ct;
int &ret = dp[pos][ct][less];
if (ret != -1)
return ret;
ret = 0;
for (int d = 0; d <= (less ? 9 : num[pos] - '0'); d++)
ret += dfs(pos + 1, ct + (d == 1), less || d < num[pos] - '0');
return ret;
}
int NumOf1(int n)
{
sprintf(num, "%d", n);
len = strlen(num);
memset(dp, 0xff, sizeof(dp));
return dfs(0, 0, 0);
}
希望,更多的人,提出优化方案。
==========
32.
有两个序列a,b,大小都为n,序列元素的值任意整数,无序;
要求:通过交换a,b中的元素,使[序列a元素的和]与[序列b元素的和]之间的差最小。
例如:
var a=[100,99,98,1,2, 3];
var b=[1, 2, 3, 4,5,40];
求解思路:
当前数组a和数组b的和之差为
A = sum(a) - sum(b)
a的第i个元素和b的第j个元素交换后,a和b的和之差为
A' = sum(a) - a[i] + b[j] - (sum(b) - b[j] + a[i])
= sum(a) - sum(b) - 2 (a[i] - b[j])
= A - 2 (a[i] - b[j])
设x = a[i] - b[j]
|A| - |A'| = |A| - |A-2x|
假设A > 0,
当x 在 (0,A)之间时,做这样的交换才能使得交换后的a和b的和之差变小,
x越接近A/2效果越好,
如果找不到在(0,A)之间的x,则当前的a和b就是答案。
所以算法大概如下:
在a和b中寻找使得x在(0,A)之间并且最接近A/2的i和j,交换相应的i和j元素,
重新计算A后,重复前面的步骤直至找不到(0,A)之间的x为止。
/
算法
1. 将两序列合并为一个序列,并排序,为序列Source
2. 拿出最大元素Big,次大的元素Small
3. 在余下的序列S[:-2]进行平分,得到序列max,min
4. 将Small加到max序列,将Big加大min序列,重新计算新序列和,和大的为max,小的为min。
def mean( sorted_list ):
if not sorted_list:
return (([],[]))
big = sorted_list[-1]
small = sorted_list[-2]
big_list, small_list = mean(sorted_list[:-2])
big_list.append(small)
small_list.append(big)
big_list_sum = sum(big_list)
small_list_sum = sum(small_list)
if big_list_sum > small_list_sum:
return ( (big_list, small_list))
else:
return (( small_list, big_list))
tests = [ [1,2,3,4,5,6,700,800],
[10001,10000,100,90,50,1],
range(1, 11),
[12312, 12311, 232, 210, 30, 29, 3, 2, 1, 1]
]
for l in tests:
l.sort()
print
print "Source List:/t", l
l1,l2 = mean(l)
print "Result List:/t", l1, l2
print "Distance:/t", abs(sum(l1)-sum(l2))
print '-*'*40
输出结果
Source List: [1, 2, 3, 4, 5, 6, 700, 800]
Result List: [1, 4, 5, 800] [2, 3, 6, 700]
Distance: 99
-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Source List: [1, 50, 90, 100, 10000, 10001]
Result List: [50, 90, 10000] [1, 100, 10001]
Distance: 38
-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Source List: [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
Result List: [2, 3, 6, 7, 10] [1, 4, 5, 8, 9]
Distance: 1
-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*-*
Source List: [1, 1, 2, 3, 29, 30, 210, 232, 12311, 12312]
Result List: [1, 3, 29, 232, 12311] [1, 2, 30, 210, 12312]
Distance: 21
33.实现一个挺高级的字符匹配算法:
给一串很长字符串,要求找到符合要求的字符串,例如目的串:123
1******3***2 ,12*****3这些都要找出来
其实就是类似一些和谐系统。。。。。
分析:
自然匹配就是对待匹配的每个字符挨个匹配
设你的待匹配字串长度位n,模式字符串长度位m.
对于待匹配字符串中的任意一个字符最坏情况下要匹配m次,也就是说这个字符不在模式字符串中。
所以最坏情况下总共是m*n此匹配,时间复杂度就是O(m*n)
倘若使用hash表对待字符串进行hash处理O(n)的时间复杂度,那么对于模式字符串中的任意字符,
仅需一次hash判断就可以得知是否在待匹配字符串中出现。
最坏仅需m次就可以得到结果。时间复杂度为O(m)或者O(n);
与此题相类似:
就是给一个很长的字符串str 还有一个字符集比如{a,b,c} 找出str里包含{a,b,c}的最短子串。
要求O(n)?
比如,字符集是a,b,c,字符串是abdcaabcx,则最短子串为abc。
用两个变量 front rear 指向一个的子串区间的头和尾
用一个int cnt[255]={0}记录当前这个子串里 字符集a,b,c 各自的个数,
一个变量sum记录字符集里有多少个了
rear 一直加,更新cnt[]和sum的值,直到 sum等于字符集个数
然后front++,直到cnt[]里某个字符个数为0,这样就找到一个符合条件的字串了
继续前面的操作,就可以找到最短的了。
//还有没有人,对此题了解的比较深的? 望 也多阐述下...:)。
34.实现一个队列。
队列的应用场景为:
一个生产者线程将int类型的数入列,一个消费者线程将int类型的数出列
生产者消费者线程演示
一个生产者线程将int类型的数入列,一个消费者线程将int类型的数出列
#include <windows.h>
#include <stdio.h>
#include <process.h>
#include <iostream>
#include <queue>
using namespace std;
HANDLE ghSemaphore; //信号量
const int gMax = 100; //生产(消费)总数
std::queue<int> q; //生产入队,消费出队
//生产者线程
unsigned int __stdcall producerThread(void* pParam)
{
int n = 0;
while(++n <= gMax)
{
//生产
q.push(n);
cout<<"produce "<<n<<endl;
ReleaseSemaphore(ghSemaphore, 1, NULL); //增加信号量
Sleep(300);//生产间隔的时间,可以和消费间隔时间一起调节
}
_endthread(); //生产结束
return 0;
}
//消费者线程
unsigned int __stdcall customerThread(void* pParam)
{
int n = gMax;
while(n--)
{
WaitForSingleObject(ghSemaphore, 10000);
//消费
q.pop();
cout<<"custom "<<q.front()<<endl; //小肥杨指出,原答案这句和上句搞错了顺序?
Sleep(500);//消费间隔的时间,可以和生产间隔时间一起调节
}
//消费结束
CloseHandle(ghSemaphore);
cout<<"working end."<<endl;
_endthread();
return 0;
}
void threadWorking()
{
ghSemaphore = CreateSemaphore(NULL, 0, gMax, NULL); //信号量来维护线程同步
cout<<"working start."<<endl;
unsigned threadID;
HANDLE handles[2];
handles[0] = (HANDLE)_beginthreadex(
NULL,
0,
producerThread,
nullptr,
0,
&threadID);
handles[1] = (HANDLE)_beginthreadex(
NULL,
0,
customerThread,
nullptr,
0,
&threadID);
WaitForMultipleObjects(2, handles, TRUE, INFINITE);
}
int main()
{
threadWorking();
getchar();
return 0;
}
35.
求一个矩阵中最大的二维矩阵(元素和最大).如:
1 2 0 3 4
2 3 4 5 1
1 1 5 3 0
中最大的是:
4 5
5 3
要求:(1)写出算法;(2)分析时间复杂度;(3)用C写出关键代码
此第35题与第3题相类似,一个是求最大子数组和,一个是求最大子矩阵和。
3.求子数组的最大和
题目:
输入一个整形数组,数组里有正数也有负数。
数组中连续的一个或多个整数组成一个子数组,每个子数组都有一个和。
求所有子数组的和的最大值。要求时间复杂度为O(n)。
例如输入的数组为1, -2, 3, 10, -4, 7, 2, -5,和最大的子数组为3, 10, -4, 7, 2,
int maxSum(int* a, int n)
{
int sum=0;
int b=0;
for(int i=0; i<n; i++)
{
if(b<=0) //此处修正下,把b<0改为 b<=0
b=a[i];
else
b+=a[i];
if(sum<b)
sum=b;
}
return sum;
}
//
解释下:
例如输入的数组为1, -2, 3, 10, -4, 7, 2, -5,
那么最大的子数组为3, 10, -4, 7, 2,
因此输出为该子数组的和18
所有的东西都在以下俩行,
即:
b:0 1 -1 3 13 9 16 18 7
sum:0 1 1 3 13 13 16 18 18
其实算法很简单,当前面的几个数,加起来后,b<0后,
把b重新赋值,置为下一个元素,b=a[i]。
当b>sum,则更新sum=b;
若b<sum,则sum保持原值,不更新。:)。July、10/31。
///
现在回到我们的最初的最大子矩阵的问题,
假设最大子矩阵的结果为从第r行到k行、从第i列到j列的子矩阵,
如下所示(ari表示a[r][i],假设数组下标从1开始):
| a11 …… a1i ……a1j ……a1n |
| a21 …… a2i ……a2j ……a2n |
.....
| ar1 …… ari ……arj ……arn | 第r行 . . .
.......... |
V
| ak1 …… aki ……akj ……akn | 第k行 . . .
.....
| an1 …… ani ……anj ……ann |
那么我们将从第r行到第k行的每一行中相同列的加起来,可以得到一个一维数组如下:
(ar1+……+ak1, ar2+……+ak2, ……,arn+……+akn)
由此我们可以看出最后所求的就是此一维数组的最大子断和问题,
到此我们已经将问题转化为上面的已经解决了的问题了。
ar1
..
ak1
注,是竖直方向,相加
//有误之处,肯定指正。:)。
#include <iostream>
2 using namespace std;
3
4 int ** a;
5 int **sum;
6 int max_array(int *a,int n)
7 {
8 int *c = new int [n];
9 int i =0;
10 c[0] = a[0];
11 for(i=1;i<n;i++)
12 {
13 if(c[i-1]<0)
14 c[i] = a[i];
15 else
16 c[i] = c[i-1]+a[i];
17 }
18 int max_sum = -65536;
19 for(i=0;i<n;i++)
20 if(c[i]>max_sum)
21 max_sum = c[i];
22 delete []c;
23 return max_sum;
24
25 }
26 int max_matrix(int n)
27 {
28 int i =0;
29 int j = 0;
30 int max_sum = -65535;
31 int * b = new int [n];
32
33 for(i=0;i<n;i++)
34 {
35 for(j=0;j<n;j++)
36 b[j]= 0;
37 for(j=i;j<n;j++)
//把数组从第i行到第j行相加起来保存在b中,在加时,自底向上,首先计算行间隔(j-i)等于1的情况,
//然后计算j-i等于 2的情况,一次类推,在小间隔的基础上一次累加,避免重复计算
38 {
39 for(int k =0;k<=n;k++)
40 b[k] += a[j][k];
41 int sum = max_array(b,n);
42 if(sum > max_sum)
3 max_sum = sum;
44 }
45 }
46 delete []b;
47 return max_sum;
48 }
49 int main()
50 {
51 int n;
52 cin >> n;
53
54 a = new int *[n];
55 sum = new int *[n];
56 int i =0;
57 int j =0;
58 for(i=0;i<n;i++)
59 {
60 sum[i] = new int[n];
61 a[i] = new int[n];
62 for(j=0;j<n;j++)
63 {
64 cin>>a[i][j];
65 sum[i][j] =0 ;
//sum[r][k]表示起始和结尾横坐标分别为r,k时的最大子矩阵
66 //sum[r][k] = max{sum (a[i][j]):r<=i<=k}:0<=k<=n-1
67 }
68 }
69 /*
70 int b[10]={31,-41,59,26,-53,58,97,-93,-23,84};
71 cout << max_array(b,10) << endl;
72 */
73 cout << max_matrix(n);
74 }
我们再来分析下这段,代码,为了让你真正弄透它。:)。
//July,11.14.
求最大子矩阵,我们先按给的代码的思路来:
1.求最大子矩阵,我们把矩阵中,每一竖直方向的排列,看做一个元素。
所以,矩阵就转化成了我们熟悉的一维数组。
即以上矩阵,相当于:
a[1->n][1] a[1->n][2] ... a[1->n][i] .. a[1->n][j] .. a[1->n][n]
1->n表示竖直方向,同一列的元素相加。
那么,假设最大子矩阵,是在第r行->第k行,所有元素的和。
| ar1 …… ari ……arj ……arn |
| . . . . |
| . . . . |
| ak1 …… aki ……akj ……akn |
所以题目就转化成了类似第3题的思路。
2.先把这第r行->k行的列的元素,分别相加。
即这段代码:
26 int max_matrix(int n)
27 {
28 int i =0;
29 int j = 0;
30 int max_sum = -65535;
31 int * b = new int [n];
32
33 for(i=0;i<n;i++)
34 {
35 for(j=0;j<n;j++)
36 b[j]= 0;
37 for(j=i;j<n;j++)
//把数组从第i行到第j行相加起来保存在b中,在加时,自底向上,
//首先计算行间隔(j-i)等于1的情况,然后计算j-i等于 2的情况,
//一次类推,在小间隔的基础上一次累加,避免重复计算
38 {
39 for(int k =0;k<=n;k++)
40 b[k] += a[j][k];
41 int sum = max_array(b,n);
42 if(sum > max_sum)
3 max_sum = sum;
44 }
45 }
46 delete []b;
47 return max_sum;
48 }
咱们,来稍微分析下,
即,求这段矩阵的和
i行 a[i][1] a[r][2] ... a[r][k] .. a[r][n]
| a[i+1][1]
...
v a[j-1][1]
j行 a[j][1] a[j][2] ... a[j][k] .. a[j][n]
for(i=0;i<n;i++) //第i行
{
for(j=0;j<n;j++) //第j行
b[j]=0; //先把b[j]初始化为 0
for(j=i;j<n;j++) //第i行->第j行 固定行
{
for(int k=0;k<=n;k++) //从上而下,列元素相加
b[k] += a[j][k];
//相加之后,调用上述的求和函数max_array(b,n)即可。
int sum=max_array(b,n);
if(sum>max_sum)
max_sum=sum; //sum->b的结果
}
}
delete []b;
return max_sum;
至于求和max_array(int* a,int n)函数,
6 int max_array(int *a,int n)
7 {
8 int *c = new int [n];
9 int i =0;
10 c[0] = a[0];
11 for(i=1;i<n;i++)
12 {
13 if(c[i-1]<0)
14 c[i] = a[i];
15 else
16 c[i] = c[i-1]+a[i];
17 }
18 int max_sum = -65536;
19 for(i=0;i<n;i++)
20 if(c[i]>max_sum)
21 max_sum = c[i];
22 delete []c;
23 return max_sum;
24
25 }
代码,则与这个差不多:
int maxSum(int* a, int n)
{
int sum=0;
int b=0;
for(int i=0; i<n; i++)
{
if(b<0) //其实,此处b<0,亦可。无需b<=0.
b=a[i];
else
b+=a[i];
if(sum<b)
sum=b;
}
return sum;
}
例如输入的数组为1, -2, 3, 10, -4, 7, 2, -5,
那么最大的子数组为3, 10, -4, 7, 2,
因此输出为该子数组的和18
所有的东西都在以下俩行,
即:
b:0 1 -1 3 13 9 16 18 7
sum:0 1 1 3 13 13 16 18 18
最后,矩阵之和,在main函数里,调用这个函数cout << max_matrix(n);输出即可。
有误之处,欢迎指正。
另外,调换俩个for循环的顺序,是否更精准?
for(i=0;i<n;i++) //第i行
{
for(j=0;j<n;j++) //第j行
b[j]=0; //先把b[j]初始化为 0
for(int k=0;k<=n;k++) //固定一列,然后0列->k列—>n列,逐级+。
{
for(j=i;j<n;j++) //第i行->第j行->第n行+ +++
//调换俩个for循环的顺序,是否更精准?
b[k] += a[j][k];
//相加之后,调用上述的求和函数max_array(b,n)即可。
int sum=max_array(b,n);
if(sum>max_sum)
max_sum=sum; //sum->b的结果
}
}
delete []b;
return max_sum;
完。:)
36.引用自网友:longzuo
谷歌笔试:
n支队伍比赛,分别编号为0,1,2。。。。n-1,已知它们之间的实力对比关系,
存储在一个二维数组w[n][n]中,w[i][j] 的值代表编号为i,j的队伍中更强的一支。
所以w[i][j]=i 或者j,现在给出它们的出场顺序,并存储在数组order[n]中,
比如order[n] = {4,3,5,8,1......},那么第一轮比赛就是 4对3, 5对8。.......
胜者晋级,败者淘汰,同一轮淘汰的所有队伍排名不再细分,即可以随便排,
下一轮由上一轮的胜者按照顺序,再依次两两比,比如可能是4对5,直至出现第一名
编程实现,给出二维数组w,一维数组order 和 用于输出比赛名次的数组result[n],求出result。
#include <stdio.h>
#include <list>
#include <iostream>
void raceResult(int** w, int* order, int* result, int n)
{
std::list<int> winer;
int count = n;
while(n)
{
winer.push_front(order[--n]);
}
int resultNum = count - 1;
int nFirst, nSecond;
int round = 1;
while(winer.size() > 1)
{
//一轮开始
std::cout<<std::endl<<"round "<<round++<<std::endl;
std::list<int>::iterator it = winer.begin();
while (it != winer.end())
{
nFirst = *it;
if (++it == winer.end())
{
//轮空
std::cout<<nFirst<<" rest this round"<<std::endl;
}
else
{
nSecond = *it;
int nWiner = *((int*)w + count * nFirst + nSecond);
if (nWiner == nFirst)
{
it = winer.erase(it);
result[resultNum--] = nSecond;
std::cout<<nFirst<<" kick out "<<nSecond<<std::endl;
}
else
{
it = winer.erase(--it);
result[resultNum--] = nFirst;
++it;
std::cout<<nSecond<<" kick out "<<nFirst<<std::endl;
}
}
}
}
if (winer.size() == 1)
{
result[0] = winer.front();
}
std::cout<<std::endl<<"final result: ";
int nPlace = 0;
while(nPlace < count)
{
std::cout<<std::endl<<result[nPlace++];
}
}
void test()
{
//team 2>team 1>team 3>team 0>team 4>team 5
int w[6][6] = {
0,1,2,3,0,0,
1,1,2,1,1,1,
2,2,2,2,2,2,
3,1,2,3,3,3,
0,1,2,3,4,5
};
int order[6] = {1,3,4,2,0,5};
int result[6] = {-1};
raceResult((int**)w, order, result, 6);
getchar();
}
//自己加上主函数,测试了下,结果竟正确..
int main()
{
test();
return 0;
}
///
round 1
1 kick out 3
2 kick out 4
0 kick out 5
round 2
2 kick out 1
0 rest this round
round 3
2 kick out 0
final result:
2
0
1
5
4
3
/
37.
有n个长为m+1的字符串,
如果某个字符串的最后m个字符与某个字符串的前m个字符匹配,则两个字符串可以联接,
问这n个字符串最多可以连成一个多长的字符串,如果出现循环,则返回错误。
恩,好办法
引用 5 楼 hblac 的回复:
37. 把每个字符串看成一个图的顶点,两个字符串匹配就连一条有向边。相当于判断一个有向图
是否有环以及求它的直径
38.百度面试:
1.用天平(只能比较,不能称重)从一堆小球中找出其中唯一一个较轻的,
使用x次天平,最多可以从y个小球中找出较轻的那个,求y与x的关系式
2.有一个很大很大的输入流,大到没有存储器可以将其存储下来,而且只输入一次,如何从这个输入
流中随机取得m个记录
3.大量的URL字符串,如何从中去除重复的,优化时间空间复杂度
38,1. y=3^x
38,2. 每次输入一个记录时,随机产生一个0到1之间的随机数,
用这些随机数维护一个大小为m的堆,即可。
38,3.大量的URL字符串,如何从中去除重复的,优化时间空间复杂度
这道题见过了,解法是构造一个hash函数,把url适当散列到若干个,
比如1000个小文件中,然后在每个小文件中去除重复的url,再把他们合并。
原理是相同的url,hash之后的散列值仍然是相同的。
38,1
samsho2
我对天平称重这道题的理解是:
每次将球分成三堆,尽可能让三堆球一样多或者让其中一堆多或者少一个。
球数y和沉重次数x的关系是:
y=1 =》x=0;(显然)
y=2 =》x=1;(显然)
y=3 =》x=2;(显然)
如果y>3,也是将球分为三堆,记为A堆、B堆、C堆
if y=3k(k>1)
称重一次,就可以判断瑕疵球在哪堆,从而使得球数降为k个;
if y=3k+1(k>=1) 假设C堆多放1球,A堆和B堆进行称重
称重一次,就可以判断瑕疵球在哪堆,
if A == B ,瑕疵球在C堆,从而使得球数降为k+1个;
else 瑕疵球在轻的堆,从而使得球数降为k个;
if y=3k-1(k>=2) 假设C堆少放1球,A堆和B堆进行称重
称重一次,就可以判断瑕疵球在哪堆,
if A == B ,瑕疵球在C堆,从而使得球数降为k个;
else 瑕疵球在轻的堆,从而使得球数降为k-1个;
利用以上过程反复,可得结果。
最后的次数x = log3(y),可能在y哪里还需要做点什么修正。但复杂度就是log y
38,1.
用天平(只能比较,不能称重)从一堆小球中找出其中唯一一个较轻的,
使用x次天平 最多可以从y个小球中找出较轻的那个,求y与x的关系式
hengchun11
用天平比较二边放一样的球数:有三种可能性
第一种 左边重 说明较轻的在右边;
第二种 右边重 说明较轻的在左边;
第三种 一样重 说明较轻的不在这里面;
以上有三种可能性,在称x=1的情况下,说明 y=2是可以称出来的 y=3,也是可以的;y=4就不行
了
所以 我觉得 分成三部分来称 就可以称出最多的球
x=1 y=3
x=2 y=9
x=3 y=27
可以得出y=3的x次方
39.
网易有道笔试:
(1).
求一个二叉树中任意两个节点间的最大距离,
两个节点的距离的定义是 这两个节点间边的个数,
比如某个孩子节点和父节点间的距离是1,和相邻兄弟节点间的距离是2,优化时间空间复杂度。
(2).
求一个有向连通图的割点,割点的定义是,如果除去此节点和与其相关的边,
有向图不再连通,描述算法。
先看第39题的第1小问,
求一个二叉树中任意俩个结点之间的距离。
以前自个,写的,求二叉树中节点的最大距离...
void traversal_MaxLen(NODE* pRoot)
{
if(pRoot == NULL)
{
return 0;
};
if(pRoot->pLeft == NULL)
{
pRoot->MaxLeft = 0;
}
else //若左子树不为空
{
int TempLen = 0;
if(pRoot->pLeft->MaxLeft > pRoot->pLeft->MaxRight)
//左子树上的,某一节点,往左边大,还是往右边大
{
TempLen+=pRoot->pLeft->MaxLeft;
}
else
{
TempLen+=pRoot->pLeft->MaxRight;
}
pRoot->nMaxLeft = TempLen + 1;
traversal_MaxLen(NODE* pRoot->pLeft);
//此处,加上递归
}
if(pRoot->pRigth == NULL)
{
pRoot->MaxRight = 0;
}
else //若右子树不为空
{
int TempLen = 0;
if(pRoot->pRight->MaxLeft > pRoot->pRight->MaxRight)
//右子树上的,某一节点,往左边大,还是往右边大
{
TempLen+=pRoot->pRight->MaxLeft;
}
else
{
TempLen+=pRoot->pRight->MaxRight;
}
pRoot->MaxRight = TempLen + 1;
traversal_MaxLen(NODE* pRoot->pRight);
//此处,加上递归
}
if(pRoot->MaxLeft + pRoot->MaxRight > 0)
{
MaxLength=pRoot->nMaxLeft + pRoot->MaxRight;
}
}
// 数据结构定义
struct NODE
{
NODE* pLeft; // 左子树
NODE* pRight; // 右子树
int nMaxLeft; // 左子树中的最长距离
int nMaxRight; // 右子树中的最长距离
char chValue; // 该节点的值
};
int nMaxLen = 0;
// 寻找树中最长的两段距离
void FindMaxLen(NODE* pRoot)
{
// 遍历到叶子节点,返回
if(pRoot == NULL)
{
return;
}
// 如果左子树为空,那么该节点的左边最长距离为0
if(pRoot -> pLeft == NULL)
{
pRoot -> nMaxLeft = 0;
}
// 如果右子树为空,那么该节点的右边最长距离为0
if(pRoot -> pRight == NULL)
{
pRoot -> nMaxRight = 0;
}
// 如果左子树不为空,递归寻找左子树最长距离
if(pRoot -> pLeft != NULL)
{
FindMaxLen(pRoot -> pLeft);
}
// 如果右子树不为空,递归寻找右子树最长距离
if(pRoot -> pRight != NULL)
{
FindMaxLen(pRoot -> pRight);
}
// 计算左子树最长节点距离
if(pRoot -> pLeft != NULL)
{
int nTempMax = 0;
if(pRoot -> pLeft -> nMaxLeft > pRoot -> pLeft -> nMaxRight)
{
nTempMax = pRoot -> pLeft -> nMaxLeft;
}
else
{
nTempMax = pRoot -> pLeft -> nMaxRight;
}
pRoot -> nMaxLeft = nTempMax + 1;
}
// 计算右子树最长节点距离
if(pRoot -> pRight != NULL)
{
int nTempMax = 0;
if(pRoot -> pRight -> nMaxLeft > pRoot -> pRight -> nMaxRight)
{
nTempMax = pRoot -> pRight -> nMaxLeft;
}
else
{
nTempMax = pRoot -> pRight -> nMaxRight;
}
pRoot -> nMaxRight = nTempMax + 1;
}
// 更新最长距离
if(pRoot -> nMaxLeft + pRoot -> nMaxRight > nMaxLen)
{
nMaxLen = pRoot -> nMaxLeft + pRoot -> nMaxRight;
}
}
//很明显,思路完全一样,但书上 给的这段代码 更规范!:)。
zhoulei0907
/*
* return the depth of the tree
*/
int get_depth(Tree *tree) {
int depth = 0;
if ( tree ) {
int a = get_depth(tree->left);
int b = get_depth(tree->right);
depth = ( a > b ) ? a : b;
depth++;
}
return depth;
}
/*
* return the max distance of the tree
*/
int get_max_distance(Tree *tree) {
int distance = 0;
if ( tree ) {
// get the max distance connected to the current node
distance = get_depth(tree->left) + get_depth(tree->right);
// compare the value with it's sub trees
int l_distance = get_max_distance(tree->left);
int r_distance = get_max_distance(tree->right);
distance = ( l_distance > distance ) ? l_distance : distance;
distance = ( r_distance > distance ) ? r_distance : distance;
}
return distance;
}
解释一下,get_depth函数是求二叉树的深度,用的是递归算法:
一棵二叉树的深度就是它的左子树的深度和右子树的深度,两者的最大值加一。
get_max_distance函数是求二叉树的最大距离,也是用递归算法:
首先算出经过根节点的最大路径的距离,其实就是左右子树的深度和;
然后分别算出左子树和右子树的最大距离,三者比较,最大值就是当前二叉树的最大距离了。
这个算法不是效率最高的,因为在计算二叉树的深度的时候存在重复计算。
但应该是可读性比较好的,同时也没有改变原有二叉树的结构和使用额外的全局变量。
July:
很好。那么,咱们再来 探讨下这个二叉树的最大距离问题。
计算一个二叉树的最大距离有两个情况:
情况A: 路径经过左子树的最深节点,通过根节点,再到右子树的最深节点。
情况B: 路径不穿过根节点,而是左子树或右子树的最大距离路径,取其大者。
只需要计算这两个情况的路径距离,并取其大者,就是该二叉树的最大距离。
简单的写下算法。
1.如果根结点,为空,当然 return 0;
2.如果左子树不为空,
寻找左子树上最深的那个点(左深度)。
否则,左子树为空
不寻找。
//即最大距离不通过根结点。
//即最大距离为maxLeft =左深度+1
3.如果右子树不为空
寻找右子树上最深的那个点(右深度)。
否则,右子树为空
不寻找。
//即最大距离不通过根结点。
//即最大距离为maxRight =右深度+1
所以,最大的距离,即为
当有左,无右时,则最大距离maxLen=maxLeft(左深度)+1 //不过根结点
当有右,无左时,则最大距离maxLen=maxRight(右深度)+1 //不过根结点
当有左,也有右时,则最大距离maxLen=maxLeft(左深度)+1 + maxRight(右深度)+1 //过根结点
三者,比较,即得,最终的maxLen。
然后么最后的问题就只剩,求左子树maxLeft或者右子树maxRight的深度问题。
求一个子树,如左子树的maxLeft,即深度问题,
我们可以这么考虑,
左子树不为空,左子树上的,某一节点,往左边大,还是往右边大
往左边大,那么maxLen加上 往左边的距离, 即相当于搜索往深的那一边 左边 搜索
往右边大,那么maxLen加上 往右边的距离。 即相当于搜索往深的那一边 左边 搜索
好比 凿井一样,总要往更深的方向凿。
凿到某一个深度后,想下,是往左边一点凿,更好列,还是往右边一点点凿更好列。
总之,目的就是为了,凿到更大 的深度。
就是这个道理了。:)。
经过上述,我一番苦口婆心之后,再来看以下这段代码,是不是更加容易懂了。
:)....
void FindMaxLen(NODE* pRoot)
{
// 遍历到叶子节点,返回
if(pRoot == NULL)
{
return;
}
// 如果左子树为空,那么该节点的左边最长距离为0
if(pRoot -> pLeft == NULL)
{
pRoot -> nMaxLeft = 0;
}
// 如果右子树为空,那么该节点的右边最长距离为0
if(pRoot -> pRight == NULL)
{
pRoot -> nMaxRight = 0;
}
// 如果左子树不为空,递归寻找左子树最长距离
if(pRoot -> pLeft != NULL)
{
FindMaxLen(pRoot -> pLeft);
}
// 如果右子树不为空,递归寻找右子树最长距离
if(pRoot -> pRight != NULL)
{
FindMaxLen(pRoot -> pRight);
}
// 计算左子树最长节点距离
if(pRoot -> pLeft != NULL)
{
int nTempMax = 0;
if(pRoot -> pLeft -> nMaxLeft > pRoot -> pLeft -> nMaxRight)
{
nTempMax = pRoot -> pLeft -> nMaxLeft;
}
else
{
nTempMax = pRoot -> pLeft -> nMaxRight;
}
pRoot -> nMaxLeft = nTempMax + 1;
}
// 计算右子树最长节点距离
if(pRoot -> pRight != NULL)
{
int nTempMax = 0;
if(pRoot -> pRight -> nMaxLeft > pRoot -> pRight -> nMaxRight)
{
nTempMax = pRoot -> pRight -> nMaxLeft;
}
else
{
nTempMax = pRoot -> pRight -> nMaxRight;
}
pRoot -> nMaxRight = nTempMax + 1;
}
// 更新最长距离
if(pRoot -> nMaxLeft + pRoot -> nMaxRight > nMaxLen)
{
nMaxLen = pRoot -> nMaxLeft + pRoot -> nMaxRight;
}
}
求左子树maxLeft或者右子树maxRight的深度问题,就涉及一个递归问题了。
即我们搜索 这个树的深度时,不一直就用着递归往下搜索么。
好比凿井,当我们试探性的是往左,还是往右,更深一点,
如果,能往右,那么递归 往右凿, //即只要右子树存在,那么不断的递归右子树,找最大深度。
如果,能往左,那么递归 往左凿。 //即只要左子树存在,那么不断的递归左子树,找最大深度。
这样,井是不是 已经凿 的很深了。
很享受,这种凿井的过程,
希望,我能与更多的人,一起来凿井,越凿越要往深处凿,凿的越深越好。
同时,把每一道题目,解释的越简单易懂,则是我的目标之一。
谢谢。:)
39.
网易有道笔试:
(2).
求一个有向连通图的割点,割点的定义是,如果除去此节点和与其相关的边,
有向图不再连通,描述算法。
网友回复,有误,指正:
求无向连通图的割点集
mysword
最简单的,删掉一个点然后判断连通性,不就可以了? //这句话,道出了割点的定义。
BlueSky2008
可以更简单一些:
在深度优先树中,根结点为割点,当且仅当他有两个或两个以上的子树。
其余结点v为割点,当且仅当存在一个v的后代结点s,s到v的祖先结点之间没有反向边。
记发现时刻dfn(v)为一个节点v在深度优先搜索过程中第一次遇到的时刻。
记标号函数low(v) = min(dfn(v), low(s), dfn(w))
s是v的儿子,(v,w)是反向边。
low(v) 表示从v或v的后代能追溯到的标号最小的节点。
则非根节点v是割点,当且仅当存在v的一个儿子s,low(s) > = dfn(v)
40.百度研发笔试题
引用自:zp155334877
1)设计一个栈结构,满足一下条件:min,push,pop操作的时间复杂度为O(1)。
2)一串首尾相连的珠子(m个),有N种颜色(N<=10),
设计一个算法,取出其中一段,要求包含所有N中颜色,并使长度最短。
并分析时间复杂度与空间复杂度。
3)设计一个系统处理词语搭配问题,比如说 中国 和人民可以搭配,
则中国人民 人民中国都有效。要求:
*系统每秒的查询数量可能上千次;
*词语的数量级为10W;
*每个词至多可以与1W个词搭配
当用户输入中国人民的时候,要求返回与这个搭配词组相关的信息。
40.百度研发笔试题
引用自:zp155334877
1)设计一个栈结构,满足一下条件:min,push,pop操作的时间复杂度为O(1)。……
所以,此题的第1小题,即是借助辅助栈,保存最小值,
且随时更新辅助栈中的元素。
如先后,push 2 6 4 1 5
stack A stack B(辅助栈)
4: 5 1 //push 5,min=p->[3]=1 ^
3: 1 1 //push 1,min=p->[3]=1 | //此刻push进A的元素1小于B中栈顶元素2
2: 4 2 //push 4,min=p->[0]=2 |
1: 6 2 //push 6,min=p->[0]=2 |
0: 2 2 //push 2,min=p->[0]=2 |
push第一个元素进A,也把它push进B,
当向Apush的元素比B中的元素小, 则也push进B,即更新B。否则,不动B,保存原值。
向栈A push元素时,顺序由下至上。
辅助栈B中,始终保存着最小的元素。
然后,pop栈A中元素,5 1 4 6 2
A B ->更新
4: 5 1 1 //pop 5,min=p->[3]=1 |
3: 1 1 2 //pop 1,min=p->[3]=2 | //下文指的是这里错了。
2: 4 2 2 //pop 4,min=p->[0]=2 |
1: 6 2 2 //pop 6,min=p->[0]=2 |
0: 2 2 NULL //pop 2,min=p->[0]=NULL v
当pop A中的元素小于B中栈顶元素时,则也要pop B中栈顶元素。
index 貌似错了,修正下,
所以,此题的第1小题,即是借助辅助栈,保存最小值,
且随时更新辅助栈中的元素。
如先后,push 2 6 4 1 5
stack A stack B(辅助栈)
4: 5 1 //push 5,min=p->[3]=1 ^
3: 1 1 //push 1,min=p->[3]=1 | //此刻push进A的元素1小于B中栈顶元素2
2: 4 2 //push 4,min=p->[0]=2 |
1: 6 2 //push 6,min=p->[0]=2 |
0: 2 2 //push 2,min=p->[0]=2 |
push第一个元素进A,也把它push进B,
当向Apush的元素比B中的元素小, 则也push进B,即更新B。否则,不动B,保存原值。
向栈A push元素时,顺序由下至上。
辅助栈B中,始终保存着最小的元素。
然后,pop栈A中元素,5 1 4 6 2
A B ->更新
4: 5 1 1 //pop 5,min=p->[3]=1 |
3: 1 1 2 //pop 1,min=p->[0]=2 |
2: 4 2 2 //pop 4,min=p->[0]=2 |
1: 6 2 2 //pop 6,min=p->[0]=2 |
0: 2 2 NULL //pop 2,min=NULL v
当pop A中的元素小于B中栈顶元素时,则也要pop B中栈顶元素。
2)一串首尾相连的珠子(m个),有N种颜色(N<=10),
设计一个算法,取出其中一段……
2.就是给一个很长的字符串str 还有一个字符集比如{a,b,c} 找出str里包含{a,b,c}的最短子串。
要求O(n)?
比如,字符集是a,b,c,字符串是abdcaabcx,则最短子串为abc
用两个变量 front,rear 指向一个的子串区间的头和尾
用一个int cnt[255]={0}记录当前这个子串里 字符集a,b,c 各自的个数,
一个变量sum记录字符集里有多少个了。
rear 一直加,更新cnt[]和sum的值,直到 sum等于字符集个数
然后front++,直到cnt[]里某个字符个数为0,这样就找到一个符合条件的字串了
继续前面的操作,就可以找到最短的了。
3.
可以建立一个RDF文件,利用protege 4.0。或者自己写的RDF/XML接口也行。
在其中建立两个“描述对象”一个是国家,一个是人民。 国家之下建立一个中国,
人民。并且在关系中建立一个关系:对每个存在的国家,都have人民。
这样,每当用户输入这两个词的时候,
就利用语义框架/接口来判断一下这两个词汇的关系,返回一个值即可。
--贝叶斯分类--
其实贝叶斯分类更实用一些。 可以用模式识别的贝叶斯算法,
写一个类并且建立一个词汇-模式的表。
这个表中每个模式,也就是每个词汇都设一个域,可以叫做most-fitted word,
然后对这个分类器进行训练。
这个训练可以在初期设定一些关联词汇;也可以在用户每次正确输入查询的时候来训练。通过训练,每个单
词对应出现概率最高的单词设到最适合域里面。
然后对于每个词,都返回最适合的单词。
作者声明:
本人July 对以上公布的所有任何题目或资源享有版权。
转载以上公布的任何一题,或资源,请注明出处,及作者我本人。
向你的厚道致敬。谢谢。
July、2010年11月14日,晚,于东华理工。
(答案V0.3版完)
//完整答案V0.3版,请到我的资源下载处下载。
细数二十世纪最伟大的10大算法
细数二十世纪最伟大的十大算法
译者:July 二零一一年一月十日
------------------------------------
参考文献:
The Best of the 20th Century: Editors Name Top 10 Algorithms。
By Barry A. Cipra。地址:http://www.uta.edu/faculty/rcli/TopTen/topten.pdf。
博主说明:
1、此20世纪的十大算法,除了快速排序算法,或者快速傅里叶变换算法,其它算法只要稍作了解即可。
2、此文非最新文章,只是本人对算法比较感兴趣,所以也做翻译,学习研究下。
===============================
发明十大算法的其中几位算法大师

一、1946 蒙特卡洛方法
[1946: John von Neumann, Stan Ulam, and Nick Metropolis, all at the Los Alamos Scientific Laboratory, cook up the Metropolis algorithm, also known as the Monte Carlo method.]
1946年,美国拉斯阿莫斯国家实验室的三位科学家John von Neumann,Stan Ulam 和 Nick Metropolis
共同发明,被称为蒙特卡洛方法。
它的具体定义是:
在广场上画一个边长一米的正方形,在正方形内部随意用粉笔画一个不规则的形状,
现在要计算这个不规则图形的面积,怎么计算列?
蒙特卡洛(Monte Carlo)方法告诉我们,均匀的向该正方形内撒N(N 是一个很大的自然数)个黄豆,
随后数数有多少个黄豆在这个不规则几何形状内部,比如说有M个,
那么,这个奇怪形状的面积便近似于M/N,N越大,算出来的值便越精确。
在这里我们要假定豆子都在一个平面上,相互之间没有重叠。(撒黄豆只是一个比喻。)
蒙特卡洛方法可用于近似计算圆周率:
让计算机每次随机生成两个0到1之间的数,看这两个实数是否在单位圆内。
生成一系列随机点,统计单位圆内的点数与总点数,内接圆面积和正方形面积之比为PI:4,PI为圆周率。
(多谢网友七里河蠢才指出:S内接圆:S正=PI:4。具体,请看文下第99条评论。十六日修正),
当随机点取得越多(但即使取10的9次方个随机点时,其结果也仅在前4位与圆周率吻合)时,
其结果越接近于圆周率。
二、1947 单纯形法
[1947: George Dantzig, at the RAND Corporation, creates the simplex method for linear programming.]
1947年,兰德公司的,Grorge Dantzig,发明了单纯形方法。
单纯形法,此后成为了线性规划学科的重要基石。
所谓线性规划,简单的说,就是给定一组线性(所有变量都是一次幂)约束条件
(例如a1*x1+b1*x2+c1*x3>0),求一个给定的目标函数的极值。
这么说似乎也太太太抽象了,但在现实中能派上用场的例子可不罕见——比如对于一个公司而言,其能够投入生产的人力物力有限(“线性约束条件”),而公司的目标是利润最大化(“目标函数取最大值”),看,线性规划并不抽象吧!
线性规划作为运筹学(operation research)的一部分,成为管理科学领域的一种重要工具。
而Dantzig提出的单纯形法便是求解类似线性规划问题的一个极其有效的方法。
三、1950 Krylov子空间迭代法
[1950: Magnus Hestenes, Eduard Stiefel, and Cornelius Lanczos, all from the Institute for Numerical Analysis at the National Bureau of Standards, initiate the development of Krylov subspace iteration methods.]
1950年:美国国家标准局数值分析研究所的,马格努斯Hestenes,爱德华施蒂费尔和
科尼利厄斯的Lanczos,发明了Krylov子空间迭代法。
Krylov子空间迭代法是用来求解形如Ax=b 的方程,A是一个n*n 的矩阵,当n充分大时,直接计算变得非常
困难,而Krylov方法则巧妙地将其变为Kxi+1=Kxi+b-Axi的迭代形式来求解。
这里的K(来源于作者俄国人Nikolai Krylov姓氏的首字母)是一个构造出来的接近于A的矩阵,
而迭代形式的算法的妙处在于,它将复杂问题化简为阶段性的易于计算的子步骤。
四、1951 矩阵计算的分解方法
[1951: Alston Householder of Oak Ridge National Laboratory formalizes the decompositional approach to matrix computations.]
1951年,阿尔斯通橡树岭国家实验室的Alston Householder提出,矩阵计算的分解方法。
这个算法证明了任何矩阵都可以分解为三角、对角、正交和其他特殊形式的矩阵,
该算法的意义使得开发灵活的矩阵计算软件包成为可能。
五、1957 优化的Fortran编译器
[1957: John Backus leads a team at IBM in developing the Fortran optimizing compiler.]
1957年:约翰巴库斯领导开发的IBM的团队,创造了Fortran优化编译器。
Fortran,亦译为福传,是由Formula Translation两个字所组合而成,意思是“公式翻译”。
它是世界上第一个被正式采用并流传至今的高级编程语言。
这个语言现在,已经发展到了,Fortran 2008,并为人们所熟知。
六、1959-61 计算矩阵特征值的QR算法
[1959–61: J.G.F. Francis of Ferranti Ltd, London, finds a stable method for computing
eigenvalues, known as the QR algorithm.]
1959-61:伦敦费伦蒂有限公司的J.G.F. Francis,找到了一种稳定的特征值的计算方法,
这就是著名的QR算法。
这也是一个和线性代数有关的算法,学过线性代数的应该记得“矩阵的特征值”,计算特征值是矩阵计算的
最核心内容之一,传统的求解方案涉及到高次方程求根,当问题规模大的时候十分困难。
QR算法把矩阵分解成一个正交矩阵(希望读此文的你,知道什么是正交矩阵。:D。)与一个上三角矩阵的积,
和前面提到的Krylov 方法类似,这又是一个迭代算法,它把复杂的高次方程求根问题化简为阶段性的易于
计算的子步骤,使得用计算机求解大规模矩阵特征值成为可能。
这个算法的作者是来自英国伦敦的J.G.F. Francis。
七、1962 快速排序算法
[1962: Tony Hoare of Elliott Brothers, Ltd., London, presents Quicksort.]
1962年:伦敦的,托尼埃利奥特兄弟有限公司,霍尔提出了快速排序。
哈哈,恭喜你,终于看到了可能是你第一个比较熟悉的算法~。
快速排序算法作为排序算法中的经典算法,它被应用的影子随处可见。
快速排序算法最早由Tony Hoare爵士设计,它的基本思想是将待排序列分为两半,
左边的一半总是“小的”,右边的一半总是“大的”,这一过程不断递归持续下去,直到整个序列有序。
说起这位Tony Hoare爵士,快速排序算法其实只是他不经意间的小小发现而已,他对于计算机贡献主要包括
形式化方法理论,以及ALGOL60 编程语言的发明等,他也因这些成就获得1980 年图灵奖。
快速排序的平均时间复杂度仅仅为O(Nlog(N)),相比于普通选择排序和冒泡排序等而言,
实在是历史性的创举。
八、1965 快速傅立叶变换
[1965: James Cooley of the IBM T.J. Watson Research Center and John Tukey of Princeton
University and AT&T Bell Laboratories unveil the fast Fourier transform.]
1965年:IBM 华生研究院的James Cooley,和普林斯顿大学的John Tukey,
AT&T贝尔实验室共同推出了快速傅立叶变换。
快速傅立叶算法是离散傅立叶算法(这可是数字信号处理的基石)的一种快速算法,其时间复杂度仅为O
(Nlog(N));比时间效率更为重要的是,快速傅立叶算法非常容易用硬件实现,因此它在电子技术领域得到
极其广泛的应用。
日后,我会在我的经典算法研究系列,着重阐述此算法。
九、1977 整数关系探测算法
[1977: Helaman Ferguson and Rodney Forcade of Brigham Young University advance an integer
relation detection algorithm.]
1977年:Helaman Ferguson和 伯明翰大学的Rodney Forcade,提出了Forcade检测算法的整数关系。
整数关系探测是个古老的问题,其历史甚至可以追溯到欧几里德的时代。具体的说:
给定—组实数X1,X2,...,Xn,是否存在不全为零的整数a1,a2,...an,使得:a1 x 1 +a2 x2 + . . . + an x
n =0?
这一年BrighamYoung大学的Helaman Ferguson 和Rodney Forcade解决了这一问题。
该算法应用于“简化量子场论中的Feynman图的计算”。ok,它并不要你懂,了解即可。:D。
十、1987 快速多极算法
[1987: Leslie Greengard and Vladimir Rokhlin of Yale University invent the fast multipole
algorithm.]
1987年:Greengard,和耶鲁大学的Rokhlin发明了快速多极算法。
此快速多极算法用来计算“经由引力或静电力相互作用的N 个粒子运动的精确计算
——例如银河系中的星体,或者蛋白质中的原子间的相互作用”。ok,了解即可。
有任何意见和问题,欢迎博客上留言或评论。
完。







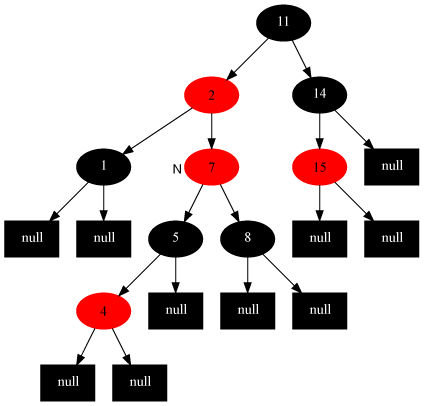
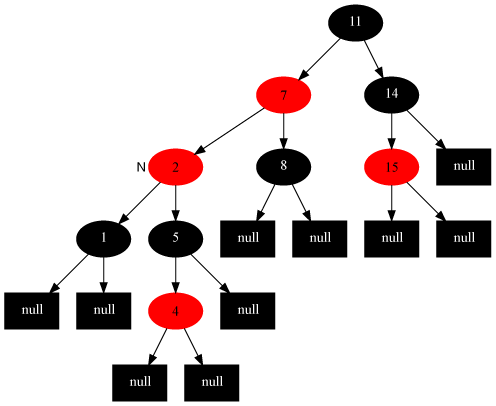
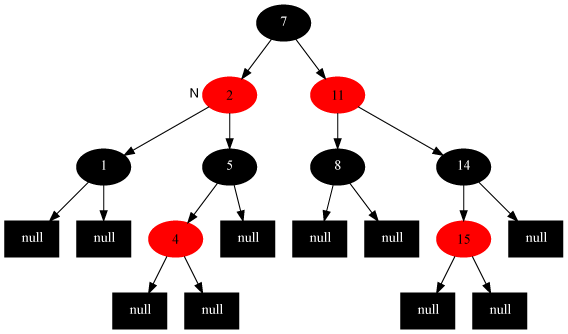
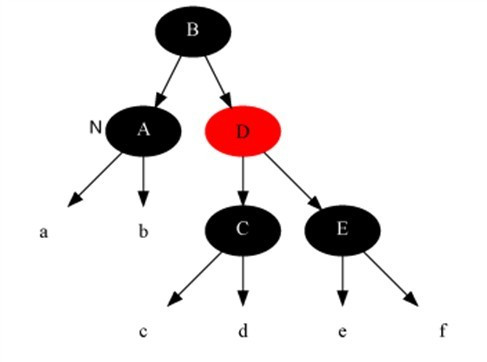
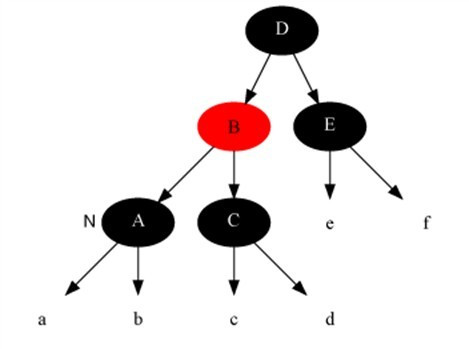
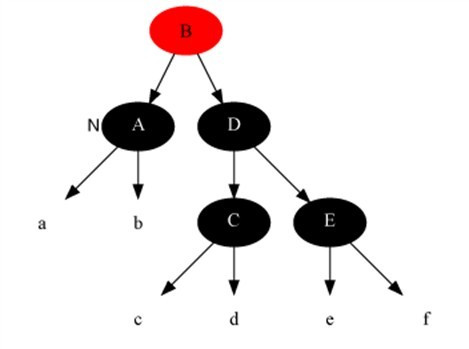
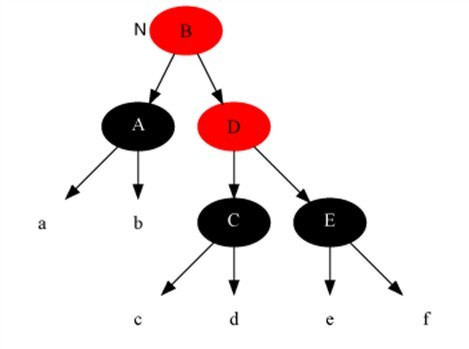
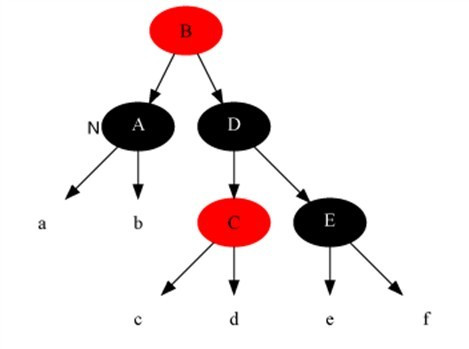
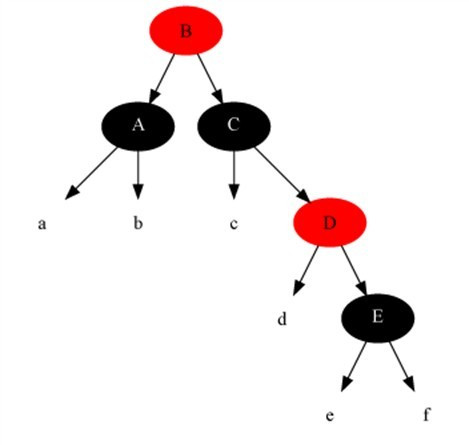
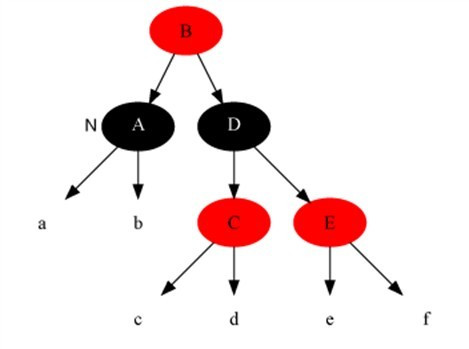

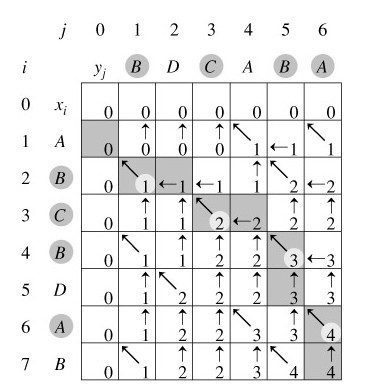
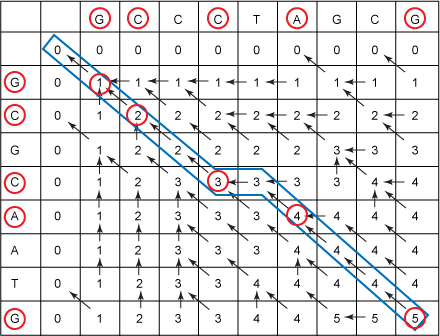
















 1043
1043

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








