【泛化误差上界（证明详推）】

最新推荐文章于 2023-06-20 19:51:00 发布
最新推荐文章于 2023-06-20 19:51:00 发布
阅读量1.1k 收藏 7
点赞数 3
分类专栏： # 泛化
原文链接：https://zhuanlan.zhihu.com/p/75486940
版权
本文深入浅出地解析了Hoeffding不等式的概念及其应用，通过具体实例展示了如何利用该不等式评估经验风险与期望风险的关系，特别关注于假设空间中函数数量有限的情况。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

转载 Cyrus

前置知识：

exp() : 以e为底的指数函数，括号内是具体内容

loge : 1.loge =lne =1

2.loge=lge=log(e) = 0.43429448190324 (摘自百度 : )笔者在一个公式上因为这个卡了15分钟）

 

好了，先给出书上定义：

 

接下来，我们要了解一下Hoeffding不等式 （咳咳，上书！！！）

emmmm一开始看到这个不等式我是有点小难受的，特别是转换到下一页的第一条公式。

没事，我们慢慢捋一捋。

然后就是这个

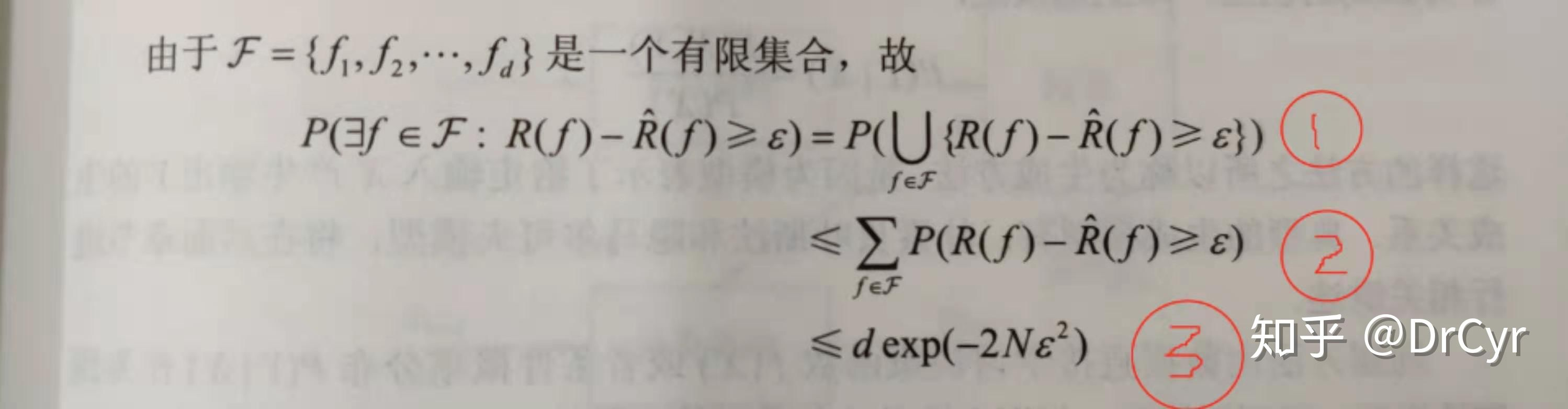
这一整个的意思是想先来求期望风险大于经验风险的概率，为后面期望风险小于经验风险公式做准备。

 

接下来基本就一路顺畅了。。。。。

 

对了，1.29那里我手写推一下，如果有疑问可以看一下hhhhh（字太丑勿喷）

以上讨论的只是假设空间包含有限个函数情况下的泛化误差上界，对一般的假设空间要找到泛化误差界就没有那么简单，这里不作介绍（严肃脸）

 

好了好了，第一章终于结束了~~~（一天下来啥都没干，真是辛苦自己了.jpg）

机器学习泛化误差上界补充推导
HEGSNS的博客
04-12 390
CSDN博文https://blog.csdn.net/SanyHo/article/details/105569224 已经给出了较为详细的推导过程，这里只给出由Hoeffding不等式退出如下不等式： P(R(f)−R^(f)≥ϵ)≤exp(−2Nϵ2)\mathbb{P}(R(f) − \hat{R}(f) \geq \epsilon) \leq exp(−2N \epsilon^2)P(R(f)−R^(f)≥ϵ)≤exp(−2Nϵ2) 的过程。 Hoeffding不等式为 P(ESn−Sn≥t)≤e
泛化误差上界的证明【内含霍夫丁不等式（Hoeffding‘s Inequality）的证明】
qq_43872529的博客
02-18 6943
本篇博客旨在补充李航老师在《统计学习方法》第一章中关于Hoeffding’s Inequality的证明，明白了它 的由来才能对泛化误差上界有更深刻的认识。 先导内容 1、 泛化能力（generalization ability）： 学习方法学习到的模型对未知数据的预测能力。 2、 泛化误差（generalization error）： 用学习到的模型对未知数据进行预测的误差，定义如下：（假设学...
期望误差和经验误差的关系——期望误差上界
https://www.cnblogs.com/qizhou/
06-20 658
　　机器学习希望最小化模型的期望(泛化)误差$L$，即模型在整个数据分布上的平均误差。然而我们只能在训练集上最小化经验误差$\hat{L}$，我们期望通过最小化经验误差来最小化泛化误差。但是训练数据和数据真实分布之间是有差异的，又根据奥卡姆剃刀原理，在训练误差相同的情况下，模型复杂度越小，泛化性能越好，因此一些理论提出使用经验误差和模型复杂度来估计模型期望误差的上界。通常表示为以下形式： $\d...
手推公式：泛化误差上界
Xurui_Luo的博客
03-02 517
介绍 本文详细推导了《统计学习方法》第一章中，泛化误差上界的不等式。其中利用到了《离散数学》、《概率论》等的知识 推导的详细过程 可能字迹不够工整，如果有问题可以发评论 ...
【统计学习笔记】泛化误差上界
qq_39573785的博客
07-08 1269
【统计学习笔记】泛化误差上界1. 泛化误差2. 泛化误差上界 1. 泛化误差 学习方法的泛化能力是指由该方法学习到的模型对未知数据的预测能力，是学习方法本质上重要的性质。测试误差是依赖于测试数据集的，泛化误差是理论上的概念，如果学到的模型是f^\hat{f}f^​，那么这个模型对未知数据预测的误差即为泛化误差： Rexp(f^)=EP[L(Y,f^(X))]=∫X×YL(y,f^(x))P(x,y)dxdy……（1)R_{exp}(\hat{f})=E_P[L(Y,\hat{f}(X))]=\int_{\m
泛化误差上界
吴智深的博客
08-20 2862
文章目录1. 损失函数与风险函数2. 泛化能力与泛化误差上界3. 相关证明3.1 马尔可夫不等式3.2 霍夫丁引理3.3 霍夫丁不等式3.4 假设空间有限的二分类问题的泛化误差上界 1. 损失函数与风险函数 机器学习中，需要通过损失函数来度量模型一次预测的好坏，通常用L(Y,f(x))L(Y,f(x))L(Y,f(x))来表示，常见的损失函数有： 0-1损失函数（指示函数） L(Y,f(X))={1,Y≠f(X)0,Y=f(X) L(Y,f(X))= \begin{cases} 1, \quad &a
【机器学习】泛化误差上界
小葵花的room
03-20 2290
泛化能力：模型对未知数据的预测能力 泛化误差：模型是f^\hat{f}f^​，该模型对于未知数据预测的误差即为泛化误差： Rexp⁡(f^)=EP[L(Y,f^(X))]=∫X×YL(y,f^(x))P(x,y)dx dy \begin{aligned} R_{\exp }(\hat{f}) &=E_{P}[L(Y, \hat{f}(X))] \\ &=\int_{\mathcal{X} \times \mathcal{Y}} L(y, \hat{f}(x)) P(x, y) \m
泛化误差上界的证明【内含霍夫丁不等式（Hoeffding’s Inequality）的证明】
01-07
霍夫丁不等式的证明一、Markov’s Inequality（马尔可夫不等式）二、Chebyshev’s Inequality（切比雪夫不等式）三、Chernoff’s bound（切诺夫...泛化误差上界进行证明一、首先我们引入霍夫丁不等式定理二、然后进入到
李航统计学习方法笔记——泛化误差上界
DamianGao的博客
03-02 1826
泛化误差上界 References 统计学习方法（第2版）李航著 p25~27 定理 对于二分类问题，当假设空间是有限个函数的集合F={f1,f2,...,fd}F=\{f_1,f_2,...,f_d\}F={f1​,f2​,...,fd​}时，对任意一个函数f∈Ff\in Ff∈F，至少以概率1−δ1-\delta1−δ，0<δ<10<\delta<10<δ&lt...
如何利用霍夫丁不等式在统计学习中估计泛化误差的上界？请结合模型预测误差的期望风险进行阐述。
11-08
为了深入理解霍夫丁不等式及其在统计学习中的应用，建议阅读《霍夫丁不等式引导的泛化误差上界证明：深度解析与应用》。这本书详细解释了泛化误差、期望风险等概念，并通过霍夫丁不等式深入剖析了泛化误差上界的计算...
在统计学习领域，如何应用霍夫丁不等式来估计泛化误差的上界，并结合模型预测误差的期望风险进行详细分析？
最新发布
11-08
为了深入理解这一过程，建议阅读《霍夫丁不等式引导的泛化误差上界证明：深度解析与应用》，该资料详细介绍了如何应用霍夫丁不等式以及相关的统计概念。 参考资源链接：[霍夫丁不等式引导的泛化误差上界证明：深度...
手推泛化误差上界公式（统计学习方法 ）
qq_41695702的博客
05-21 1150
字不好看，见谅
数学公式推导_泛化误差_generalization error
weixin_45808526的博客
08-12 664
数学公式推导_泛化误差_generalization error用到的知识推导 用到的知识 Hoeffding不等式 X1 …X2 Xn为独立随机变量 个人感觉很像切比雪夫 P[X_−E(X_)⩾t]≪exp⁡(−2N2t2ΣNi=1(bi−ai)2) P\left[ \overset{\_}{X}-E\left( \overset{\_}{X} \right) \geqslant t \right] \ll \exp \left( -\frac{2N^2t^2}{\underset{i=1}{\ove
统计学习方法笔记01_泛化误差上界
分享数据科学家的自我修养
12-08 453
文章目录Hoeffding 不等式期望损失与经验损失泛化误差上界证明[^1] Hoeffding 不等式 第 2 版， 设 X1,X2,,⋯ ,XNX_1,X_2,,\cdots,X_NX1​,X2​,,⋯,XN​ 是独立随机变量，且 Xi∈[ai,bi],i=1,2,⋯ ,NX_{i} \in [a_i,b_i],i=1,2,\cdots,NXi​∈[ai​,bi​],i=1,2,⋯,N；Xˉ\bar{X}Xˉ 是 X1,X2,,⋯ ,XNX_1,X_2,,\cdots,X_NX1​,X2​,,⋯,XN​
统计方法（李航）|第一章|泛化误差上界定理推导
zzztutu的博客
09-08 229
从李航老师的《统计方法》入门机器学习算法，记录一下自己的学习过程
机器学习（1）泛化误差上界的实现及分析
ProfSnail的博客
01-25 2046
本文在假设空间有限情况下的泛化误差上界分析，并给出了简要的C语言实现。
泛化误差上界证明
zr7116的博客
02-27 1161
统计学习方法第一章：泛化误差上界证明完整过程——Hoeffding定理证明+所有引理证明
weixin_43850920的博客
06-14 615
欢迎大家交流讨论，一起进步！
模型泛化能力(泛化误差+泛化误差上界)| 15mins 入门 | 《统计学习方法》学习笔记（六）
用途：中英文学习笔记，如有侵权，可评论留言，及时清理；学历：NUS计算机硕士；SYSU地球物理学士
04-16 2685
泛化能力 一、 泛化误差 学习方法的泛化能力（generalization ability）：方法学习到的模型对未知数据的预测能力。 评价标准：测试误差。 但因为测试数据集是有限的，很有可能由此得到的评价结果是不可靠的。统计学习理论试图从理论上对学习方法的泛化能力进行分析。 泛化误差定义：如果学习到的模型是f^\hat ff^​，那么用这个模型对未知数据预测的误差即为泛化误差（generali...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值