一、图(Graph)是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为:G(V,E),其中,G表示一个图,V是图G中顶点的集合,E是图G中边的集合。在图中的数据元素,我们称之为顶点(Vertex),顶点集合有穷非空。在图中,任意两个顶点之间都可能有关系,顶点之间的逻辑关系用边来表示,边集可以是空的。
二、图按照有无方向分为无向图和有向图。无向图由顶点和边组成,有向图由顶点和弧构成。弧有弧尾和弧头之分,带箭头一端为弧头。
三、图按照边或弧的多少分稀疏图和稠密图。如果任意两个顶点之间都存在边叫做完全图,有向的叫有向完全图。若无重复的边或顶点到自身的边则叫简单图。
四、图中顶点之间有邻接点、依附的概念。无向图顶点的边数叫做度。有向图顶点分为入度和出度。
五、图上的边或弧带有权则称为网。
六、图中顶点间存在路径,两顶点存在路径则说明是连通的,如果路径最终回到起始点则称为环,当中不重复的叫简单路径。若任意两顶点都是连通的,则图就是连通图,有向则称为强连通图。图中有子图,若子图极大连通则就是连通分量,有向的则称为强连通分量。
七、无向图中连通且n个顶点n-1条边称为生成树。有向图中一顶点入度为0其余顶点入度为1的叫有向树。一个有向图由若干棵有向树构成生成森林。
图的邻接矩阵(Adjacency Matrix)存储方式是用两个数组来表示图。一个一维的数组存储图中顶点信息,一个二维数组(称为邻接矩阵)存储图中的边或弧的信息。
设图G有n个顶点,则邻接矩阵是一个n*n的方阵,定义为:
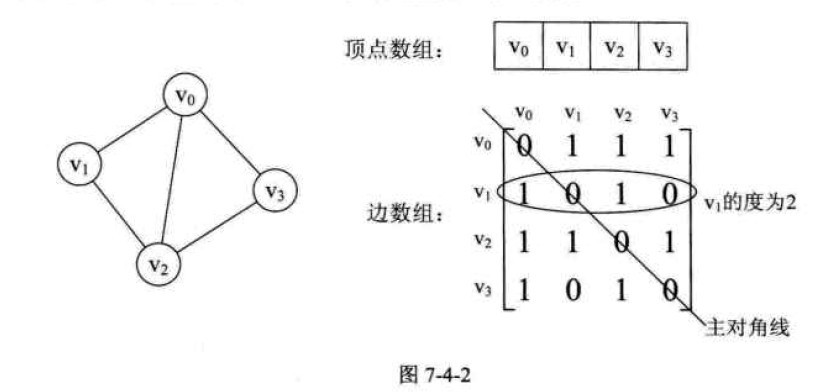
我们来看一个实例,图7-4-2的左图就是一个无向图。
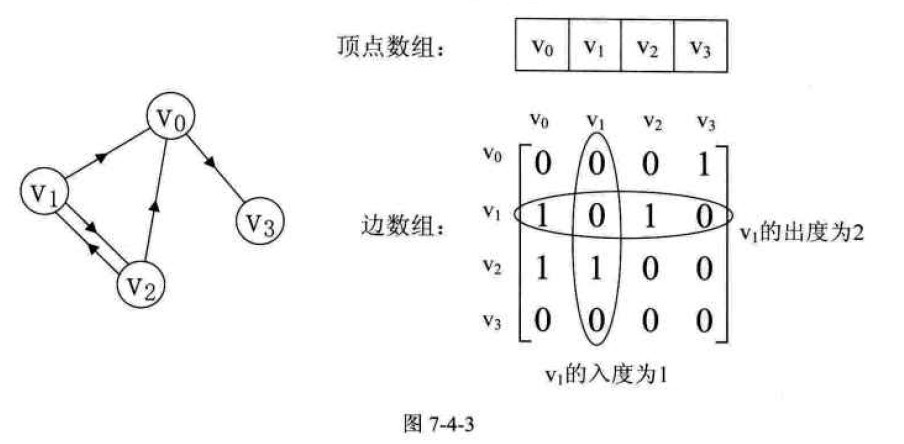
我们再来看一个有向图样例,如图7-4-3所示的左图。
在图的术语中,我们提到了网的概念,也就是每条边上都带有权的图叫做网。那些这些权值就需要保存下来。
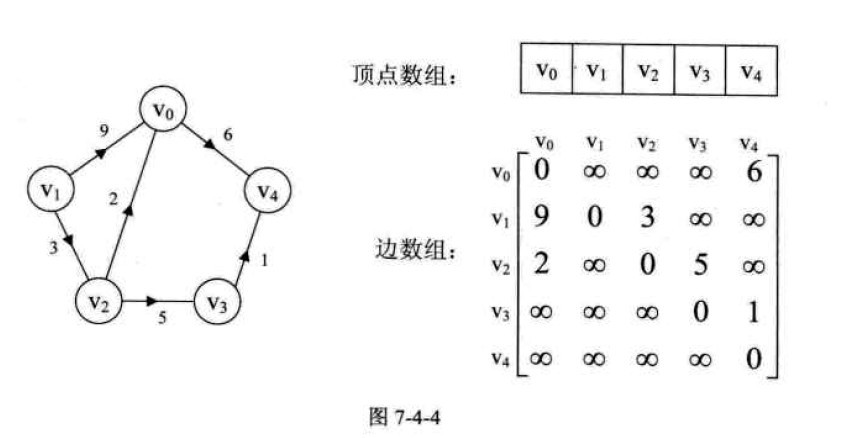
设图G是网图,有n个顶点,则邻接矩阵是一个n*n的方阵,定义为:
如图7-4-4左图就是一个有向网图。
原文:http://blog.csdn.net/jnu_simba/article/details/8866705








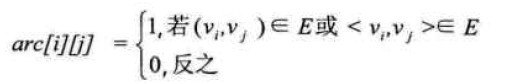
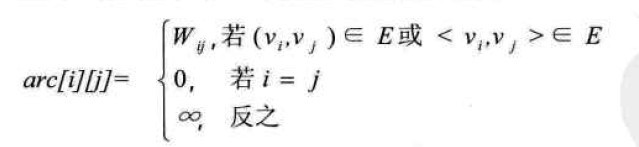
















 5081
5081

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








