HDU4568/2013年长沙赛区Hunter

Description

One day, a hunter named James went to amysterious area to find the treasures. James wanted to research the area andbrought all treasures that he could.

The area can be represented as aN*Mrectangle. Any points of the rectangle is a number means the cost of researchit,-1 means James can't cross it, James can start at any place out of therectangle, and explore point next by next. He will move in the rectangle andbring out all treasures he can take. Of course, he will end at any border to goout of rectangle(James will research every point at anytime he cross because hecan't remember whether the point are researched or not).

Now give you a map of the area, you mustcalculate the least cost that James bring out all treasures he can take(onepoint up to only one treasure).Also, if nothing James can get, please output 0.

 

 

Input

 

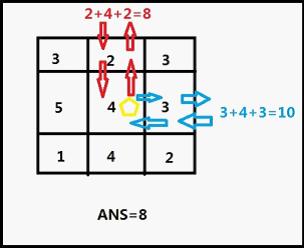
Input

The input consists of T test cases. Thenumber of test cases T is given in the first line of the input. Each test casebegins with a line containing 2 integersN M, (1<=N,M<=200),that represents the rectangle. Each of the followingN lines containsMnumbers(0~9),represent the cost of each point. Next isK(1<=K<=13),andnextK lines, each line contains 2 integersx y means theposition of the treasures,x means row and start from 0,y meanscolumn start from 0 too.

 

Output

For each test case, you should output onlya number means the minimum cost.

Sample Input

2

3 3

3 2 3

5 4 3

1 4 2

1

1 1

3 3

3 2 3

5 4 3

1 4 2

2

1 1

2 2

 

Sample Output

8

11

读入地图，用SPFA对图做预处理，求出所有宝物和地图外构成的图的任意两点的最短距离，然后用状态压缩DP得解。

 

#include <stdio.h>
#include <cstring>
#include <string>
#include <algorithm>
#include <queue>

using namespace std;

typedef long long LL;

const int MAXM = 14;
const int MAXN = 1<<MAXM;
const int INF = 1000000000;

int n, m, treasure;
int mp[210 * 210], dis[210 * 210] , pos_treasure[20][2], value[MAXM];
int dp[MAXN][MAXM], g[20][20];
int dx[4] = {0, 0, -1, 1};
int dy[4] = {-1, 1, 0, 0};

// 40000 * 13 * range(mp[]) is integer?
// if some treasure in the gride of value -1 ?
// if some treasure is surround the -1

int get_id(int r, int c){
    if(r >= 0 && r < n && c >= 0 && c < m)  return r * m + c;
    return n * m;
}
queue<int> q;
bool inq[210 * 210];

void spfa(int s){
    for(int i = 0; i <= n * m; ++i)
        dis[i] = INF;

    dis[s] = (mp[s] == -1 ? INF : mp[s]);
    while(!q.empty())  q.pop();
    q.push(s);
    memset(inq, 0, sizeof(inq));
    int out = n * m;

    while(!q.empty()){
        int u = q.front();  q.pop(); inq[u] = 0;
        if(u == out)  continue;
        int r = u / m;
        int c = u % m;

        for(int i = 0; i < 4; ++i){
            int nr = r + dx[i];
            int nc = c + dy[i];

            int id = get_id(nr, nc);
            if(mp[id] == -1)  continue;

            if(dis[id] > dis[u] + mp[id]){
                dis[id] = dis[u] + mp[id];
          //      printf("%d %d -> %d %d   %d   %d   %d   %d\n", r, c, nr, nc,id, dis[id], dis[u], mp[id]);
                if(!inq[id])  q.push(id);
                inq[id] = 1;
            }
        }

    }
}
int make(){

    for(int i = 0; i < treasure; ++i){
        spfa( pos_treasure[i][0] * m + pos_treasure[i][1]);
        for(int j = 0; j < treasure; ++j) {
            g[i][j] = dis[get_id(pos_treasure[j][0], pos_treasure[j][1])];
            if(g[i][j] == INF)  return 0;
        }
        g[i][treasure] = dis[n * m];
    }
//#if 1
//    for(int i = 0; i < treasure; ++i) {
//        for(int j = 0; j <= treasure; ++j){
//            printf("%d ", g[i][j]);
//        }
//        puts("");
//    }
//#endif
    return 1;
}

int solve(){
    if(treasure == 0)  return 0;
    int full = 1<<treasure;
    for(int i = 0; i < full; ++i)
        for(int j = 0; j < treasure; ++j)
            dp[i][j] = INF;
    for(int i = 0; i < treasure; ++i) {
        dp[1<<i][i] = g[i][treasure];
    }

    for(int i = 1; i < full; ++i){
        for(int j = 0; j < treasure; ++j){
            for(int k = 0; k < treasure; ++k){
                if( (i & (1<<j)) && (i & (1<<k)) && j != k){
                    if(dp[i ^ (1<<k)][j] != INF) dp[i][k] = min(dp[i][k], dp[i ^ (1<<k) ][j] + g[j][k] - value[j]);
                }
            }
        }
    }

    int res(INF);
    for(int i = 0; i < treasure; ++i){
        res = min(res, dp[full - 1][i] + g[i][treasure] - value[i]);
    }
    return res;
}
void readin(){

    scanf("%d%d", &n, &m);
    for(int i = 0; i < n; ++i){
        for(int j = 0; j < m; ++j){
            scanf("%d", &mp[i * m + j]);
        }
    }
#if 0
    for(int i = 0; i < n; ++i){
        for(int j = 0; j < m; ++j){
            printf("%d ", mp[i * m + j]);
        }puts("");
    }
#endif
    scanf("%d", &treasure);
    for(int i = 0; i < treasure; ++i){
        scanf("%d%d", &pos_treasure[i][0], &pos_treasure[i][1]);
        int id = get_id(pos_treasure[i][0], pos_treasure[i][1]);
        value[i] = mp[id];
    }
    mp[n * m] = 0;
}

int main(){
    int test;
    scanf("%d", &test);
    while(test--){
        readin();
        if(make())   printf("%d\n", solve());
    }

    return 0;
}