C语言数组实现堆：高效二叉树应用指南

---

C语言数组实现堆的二叉树应用

1. 引言

• 介绍堆数据结构的重要性及其在计算机科学中的核心地位。
• 解释为什么使用数组实现堆：数组能高效表示完全二叉树，节省空间并支持快速访问。
• 概述堆的二叉树应用场景，如排序算法和优先队列。
• 目标受众：C语言开发者和算法学习者。

2. 堆与二叉树的基本概念

树：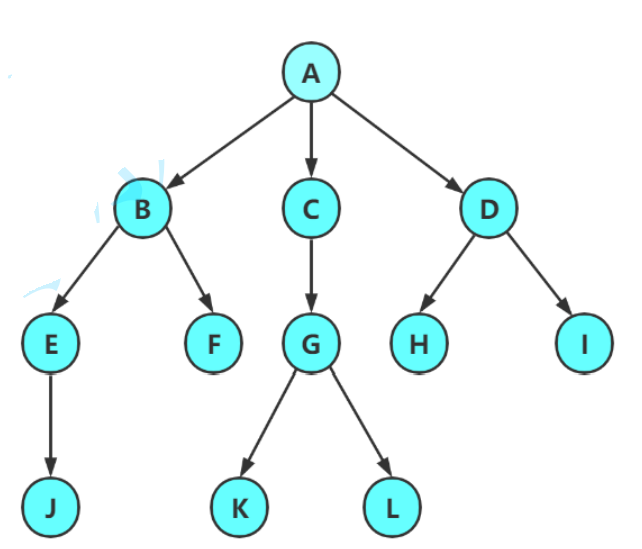

树需要满足以下几个要求

1.子树不相交

2.除了根节点没有父节点，每个结点有且仅有一个父节点

• 二叉树基础：1. 或者为空
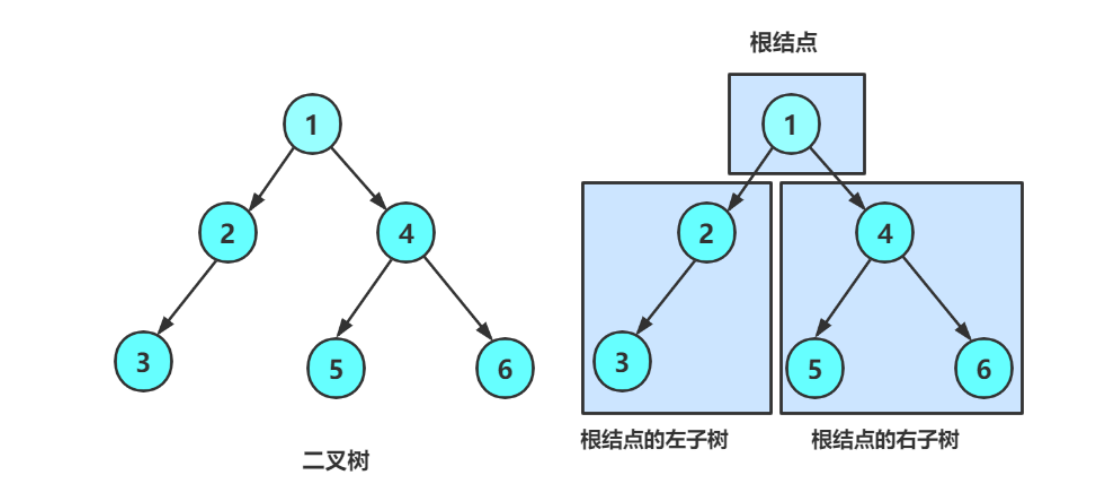
• 由上图可看出
  2. 二叉树的子树有左右之分，次序不能颠倒，因此二叉树是有序树
  • 完全二叉树特性：所有层级除最后一层外完全填充。
  • 满二叉树是完全二叉树的一种情况
  • 
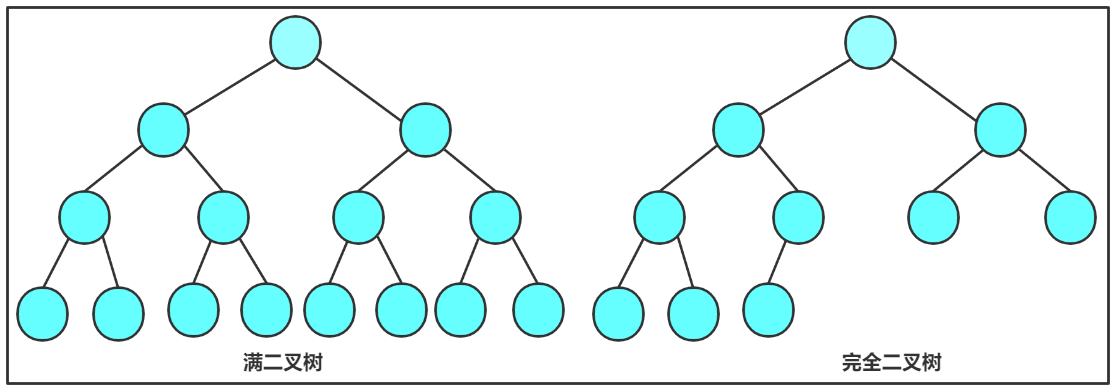
• 数组表示法：
  • 使用数组存储堆元素，索引从0开始。
  • 对于具有n个结点的完全二叉树，如果按照从上至下从左至右的数组顺序对所有结点从0开始编号，则对于序号为i的结点有：
    1. 若i>0，i位置结点的双亲序号：(i-1)/2；i=0，i为根结点编号，无双亲结点
    2. 若2i+1<n，左孩子序号：若2i+1，2i+1>=n否则无左孩子
    3. 若2i+2<n，右孩子序号：若2i+2，2i+2>=n否则无右孩子
  • 优势：时间复杂度O(1)访问，空间利用率高。

3. C语言数组实现堆的核心步骤

• 堆的定义：
  • 堆是一种特殊满足堆属性的完全二叉树

堆是对于二叉树结构的应用，具有顺序属性

堆的性质：堆中某个结点的值总是不大于或不小于其父结点的值；堆总是一棵完全二叉树

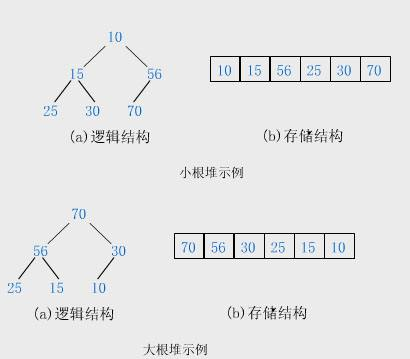
• 数据结构定义：

  typedef int HPDataType;
  
  typedef struct Heap
  {
  	HPDataType* arr;
  	int size;
  	int capacity;
  }HP;

  • 定义堆结构体：包含数组指针、当前大小和容量。
• 堆的初始化与销毁：
  • 创建堆函数：分配内存并设置初始值。

  void HP_Init(HP* php)
  {
  	assert(php);
  	php->arr = NULL;
  	php->capacity = php->size = 0;
  }

  • 释放资源函数：避免内存泄漏。

void HP_Destroy(HP* php)
{
	assert(php);
	free(php->arr);
	php->arr = NULL;
	php->capacity = php->size = 0;
}

• 关键操作实现：

  //交换数据
  void swap(int* p1,int* p2)
  {
  	HPDataType temp = *p1;
  	*p1 = *p2;
  	*p2 = temp;
  }
  

  swap函数用于交换两个值

  • 插入元素（用到向上调整）：
    • 步骤：添加元素到末尾，然后上滤调整以满足堆属性。
    • 时间复杂度：O(log n)。

  //插入
  void HP_Push(HP* php, HPDataType x)
  {
  	assert(php);
  	//判断空间
  	if (php->capacity == php->size)
  	{
  		int newsize = php->capacity == 0 ? 4 : 2 * php->capacity;
  		HPDataType* newspace = (HPDataType*)realloc(php->arr, newsize * sizeof(HPDataType));
  		php->capacity = newsize;
  		if (newspace == NULL)
  		{
  			perror("realloc fail!");
  			exit(1);
  		}
  		php->arr = newspace;
  	}
  	
  	php->arr[php->size] = x;
  	php->size++;
  	//上述已经将新值插入到最后一个位置
  	Adjustup(php->arr,php->size);
  }
  
  //向上调整
  void Adjustup(int* a,int size)
  {
  	assert(a);
  	int child = size -1;
  	int parent = (child - 1) / 2;
  	while (child > 0)
  	{
  		if (a[child] > a[parent])
  		{
  			swap(&a[child], &a[parent]);
  			child = parent;
  			parent = (child - 1) / 2;
  		}
  		else
  		{
  			break;
  		}
  	}
  	
  }

  • 删除根元素（用到向下调整）：
    • 步骤：移除根元素，将末尾元素移到根位置，然后下滤调整。
    • 时间复杂度：O(log n)。

    //删除根元素
    void HP_Pop(HP* php)
    {
    	swap(&php->arr[0], &php->arr[php->size - 1]);
    	php->size--;
    	AdjustDown(php->arr,php->size,0);
    }
    
    //向下调整
    void AdjustDown(int* a,int size,int root)
    {
    	assert(a);
    	int parent = root;
    	int child = 2 * parent + 1;
    	while (child < size)
    	{
    		if (a[child] < a[child + 1])
    		{
    			child++;
    		}
    		if (a[parent] < a[child])
    		{
    			swap(&a[child], &a[parent]);
    			parent = child;
    			child = 2 * parent + 1;
    		}
    		else
    		{
    			break;
    		}
    	}
    
    }

  • 堆化（Heapify）数组：
    • 从无序数组构建堆：从最后一个非叶子节点开始下滤。
    • 时间复杂度分析：O(n)。

//N:size
for (int i = 1; i < N; i++)
{
	Adjustup(a, i);
}

4. 堆在二叉树中的应用实例

• 堆排序算法：
  • 原理：利用堆实现高效排序。
  • 步骤：
  • 时间复杂度：O(n *log n)。
  • C语言实现要点：结合数组操作优化性能。

  void HeapSort(int* a, int n)
  {
  	// 降序，建小堆
  	// 升序，建大堆
  
  	for (int i = (n-1-1)/2; i >= 0; i--)
  	{
  		AdjustDown(a, n, i);
  	}
  
  	int end = n - 1;
  	while (end > 0)
  	{
  		Swap(&a[0], &a[end]);
  		AdjustDown(a, end, 0);
  		--end;
  	}
  }

5. 优缺点分析与优化建议

• 优点：
  • 空间效率：数组紧凑存储，无指针开销。
  • 时间效率：核心操作对数时间。
• 缺点：
  • 缓存不友好：大数组可能导致缓存未命中。
• 优化策略：
  • 动态数组：使用realloc调整容量。
  • 索引优化：位运算加速索引计算（如用移位代替除法）。
  • 错误处理：添加边界检查以防止溢出。

6. 总结

• 回顾核心点：数组实现堆的高效性、二叉树应用的价值。
• 实际建议：在C语言项目中优先使用数组堆，用于性能关键场景。

---