python机器学习案例系列教程——集成学习（Bagging、Boosting、随机森林RF、AdaBoost、GBDT、xgboost）

全栈工程师开发手册 （作者：栾鹏）
python数据挖掘系列教程

可以通过聚集多个分类器的预测结果提高分类器的分类准确率，这一方法称为集成（Ensemble）学习或分类器组合（Classifier Combination），该方法由训练数据构建一组基分类器（Base Classifier），然后通过对每个基分类器的预测进行投票来进行分类。

集成学习（ensemble learning）通过组合多个基分类器（base classifier）来完成学习任务，颇有点“三个臭皮匠顶个诸葛亮”的意味。基分类器一般采用的是弱可学习（weakly learnable）分类器，通过集成学习，组合成一个强可学习（strongly learnable）分类器。所谓弱可学习，是指学习的正确率仅略优于随机猜测的多项式学习算法；强可学习指正确率较高的多项式学习算法。集成学习的泛化能力一般比单一的基分类器要好，这是因为大部分基分类器都分类错误的概率远低于单一基分类器的。

偏差与方差

“偏差-方差分解”（bias variance decomposition）是用来解释机器学习算法的泛化能力的一种重要工具。对于同一个算法，在不同训练集上学得结果可能不同。对于训练集$D={(x_1 ,y_1 ),(x_2 ,y_2 ),⋯,(x_N ,y_N )} $，由于噪音，样本$x$的真实类别为$y$（在训练集中的类别为$y$），则噪声为

$${\xi }^2=E_D[(y_d-y{)}^2]$$

各种学习模型得到的预测值的期望为

$$\widehat{f(x)}=E_D[f(x;D)]$$

使用样本数相同的不同训练集所产生的方差
$$var(x)=E_D[(f(x;D)-\widehat{f(x)}{)}^2]$$

期望输出与真实类别的差别称为bias，则

$$bia{s}^2(x)=(\widehat{f(x)}-y{)}^2$$

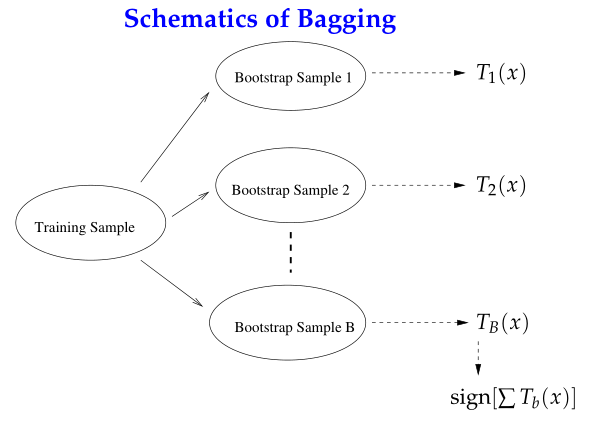
Bagging

Bagging（Bootstrap Aggregating）对训练数据采用自助采样（boostrap sampling），即有放回地采样数据；每一次的采样数据集训练出一个基分类器，经过M次采样得到M个基分类器，然后根据最大表决（majority vote）原则组合基分类器的分类结果。

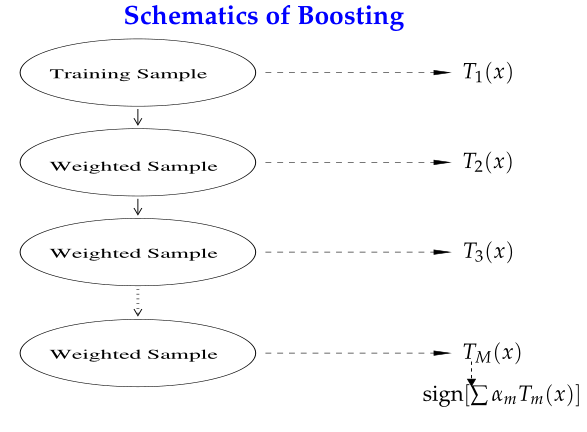
Boosting

Boosting的思路则是采用重赋权（re-weighting）法迭代地训练基分类器，即对每一轮的训练数据样本赋予一个权重，并且每一轮样本的权值分布依赖上一轮的分类结果；基分类器之间采用序列式的线性加权方式进行组合。他通过迭代地训练一系列的分类器，每个分类器采用的样本分布都和上一轮的学习结果有关。其代表算法是AdaBoost， GBDT。

从“偏差-方差分解”的角度看，Bagging关注于降低variance，而Boosting则是降低bias；Boosting的基分类器是强相关的，并不能显著降低variance。Bagging与Boosting有分属于自己流派的两大杀器：随机森林Random Forests（RF）和梯度下降树Gradient Boosting Decision Tree（GBDT）。AdaBoost属于Boosting流派。

Bagging、Boosting二者之间的区别

样本选择上：
Bagging：训练集是在原始集中有放回选取的，从原始集中选出的各轮训练集之间是独立的。
Boosting：每一轮的训练集不变，只是训练集中每个样例在分类器中的权重发生变化。而权值是根据上一轮的分类结果进行调整。

样例权重：
Bagging：使用均匀取样，每个样例的权重相等。
Boosting：根据错误率不断调整样例的权值，错误率越大则权重越大。

预测函数：
Bagging：所有预测函数的权重相等。
Boosting：每个弱分类器都有相应的权重，对于分类误差小的分类器会有更大的权重。

并行计算：
Bagging：各个预测函数可以并行生成。
Boosting：各个预测函数只能顺序生成，因为后一个模型参数需要前一轮模型的结果。

总结

这两种方法都是把若干个分类器整合为一个分类器的方法，只是整合的方式不一样，最终得到不一样的效果，将不同的分类算法套入到此类算法框架中一定程度上会提高了原单一分类器的分类效果，但是也增大了计算量。

下面是将决策树与这些算法框架进行结合所得到的新的算法：

Bagging + 决策树 = 随机森林
AdaBoost + 决策树 = 提升树
Gradient Boosting + 决策树 = GBDT

随机森林RF

理解了bagging算法，随机森林(Random Forest,以下简称RF)就好理解了。它是Bagging算法的进化版，也就是说，它的思想仍然是bagging，但是进行了独有的改进。我们现在就来看看RF算法改进了什么。

首先，RF使用了CART决策树作为弱学习器。第二，在使用决策树的基础上，RF对决策树的建立做了改进，对于普通的决策树，我们会在节点上所有的n个样本特征中选择一个最优的特征来做决策树的左右子树划分，但是RF通过随机选择节点上的一部分样本特征，这个数字小于n，假设为$n_{sub}$，然后在这些随机选择的$n_{sub}$个样本特征中，选择一个最优的特征来做决策树的左右子树划分。这样进一步增强了模型的泛化能力。

如果$n_{sub}=n$，则此时RF的CART决策树和普通的CART决策树没有区别。$n_{sub}$越小，则模型越健壮，当然此时对于训练集的拟合程度会变差。也就是说$n_{sub}$越小，模型的方差会减小，但是偏倚会增大。在实际案例中，一般会通过交叉验证调参获取一个合适的$n_{sub}$的值。
除了上面两点，RF和普通的bagging算法没有什么不同， 下面简单总结下RF的算法。

输入为样本集$D=(x_1,y_1),(x_2,y_2),...(x_m,y_m)$，弱分类器迭代次数T。输出为最终的强分类器$f(x)$:

1）对于$t=1,2...,T$：

• a)对训练集进行第t次随机采样，得到一个包含m个样本的采样集$D_m$
• b)用采样集$D_m$训练第m个决策树模型$G_m(x)$，在训练决策树模型的节点的时候， 在所有的特征中选择一部分特征，在这些随机选择的部分样本特征中选择最优的特征来做决策树的左右子树划分。

2. 如果是分类算法预测，则T个弱学习器投出最多票数的类别或者类别之一为最终类别。如果是回归算法，T个弱学习器得到的回归结果进行算术平均得到的值为最终的模型输出。

作为一个可以高度并行化的算法，RF在大数据时候大有可为。这里也对常规的随机森林算法的优缺点做一个总结。

RF的主要优点有：

1）训练可以高度并行化，对于大数据时代的大样本训练速度有优势。个人觉得这是的最主要的优点。
2）由于可以随机选择决策树节点划分特征，这样在样本特征维度很高的时候，仍然能高效的训练模型。
3）在训练后，可以给出各个特征对于输出的重要性
4）由于采用了随机采样，训练出的模型的方差小，泛化能力强。
5）相对于Boosting系列的Adaboost和GBDT， RF实现比较简单。
6）对部分特征缺失不敏感。

随机森林的准确率可以和adaboost相媲美，但是对错误和离群点更鲁棒。随机森林中树的个数增加，森林的泛化误差收敛，因此过拟合不是问题。随机森林的准确率依赖于个体分类器的实力和他们之间的依赖性。理想情况是保持个体分类的能力而不提高他们之间的相关性。随机森林对每次划分所考虑的属性数目很敏感。通常选取$lo{g}_2^d+1$个属性。

RF的主要缺点有：

1)在某些噪音比较大的样本集上，RF模型容易陷入过拟合。
2)取值划分比较多的特征容易对RF的决策产生更大的影响，从而影响拟合的模型的效果。

AdaBoost

AdaBoost是由Freund与Schapire提出来解决二分类问题$y∈{1,-1} $，其定义损失函数为指数损失函数：

$$L(y,f(x))=exp(-yf(x))$$

则整个样本集(n个样本)的整体损失函数，或者叫目标函数为

$$L(y,f(x))=\frac{1}{n}\sum _{i=1}^{n}exp(-y_{i}f(x_i))$$

我们来看看是如何根据损失函数推导出模型系数${\alpha }_m$的。由于多个基分类器总是依次出现，所以我们不会当所有分类器出现以后再计算每个分类器的权重，而是每次出现一个基分类器，我们就根据损失函数，计算当前分类器的权重。（每个分类器的权重还会影响下一个分类器的样本权重，所以必然是每训练出一个分类器，就计算一个分类器的权重）。关于为什么要使用指数损失，可以参考：https://www.cnblogs.com/willnote/p/6801496.html或者https://blog.csdn.net/thriving_fcl/article/details/50877957

根据加型模型（additive model），第m轮的分类函数

$$f_m(x)=f_{m-1}(x)+{\alpha }_m{G}_m(x)$$

其中，${\alpha }_m$为基分类器$G_m(x)$的组合系数。AdaBoost采用前向分布（forward stagewise）这种贪心算法最小化损失函数，求解子模型的${\alpha }_m$

$${\alpha }_m=\frac{1}{2}log\frac{1-e_m}{e_m}$$

其中，$e_m$为$G_m(x)$的加权分类误差率
$$e_m=\frac{{\sum }_{i=1}^N{w}_i^{(m)}I(y_i\ne G(x_i))}{{\sum }_{i=1}^N{w}_i^{(m)}}$$

第$m+1$轮的训练数据集权值分布
$D_{m+1}=(w_{m+1},1,\cdots ,w_{m+1},i,\cdots ,w_{m+1},N)$

$$w_{m+1,i}=\frac{w_{m,i}}{Z_m}exp(-{\alpha }_m{y}_i{G}_m(x_i))$$

其中，$Z_m$为规范化因子

$$Z_m=\sum _{i=1}^N{w}_{m,i}\ast exp(-{\alpha }_m{y}_i{G}_m(x_i))$$

则得到最终分类器

$$sign(f(x))=sign(\sum _{m=1}^M{\alpha }_m{G}_m(x))$$

${\alpha }_m$是$e_m$的单调递减函数，特别地，当$e_m\le 0.5$时，${\alpha }_m$ ≥0；当$e_m >12 $时，即基分类器不满足弱可学习的条件（比随机猜测好），则应该停止迭代。

具体算法流程如下：

$D_1(i)=1/N$ %初始化权重分布
for m=1,⋯,M m=1,⋯,M:
　　learn base classifier $G_m(x)$;
　　 if $e_m>0.5$ then break；
　　update ${\alpha }_m$and $D_{m+1}$;
end for

在算法第4步，学习过程有可能停止，导致学习不充分而泛化能力较差。因此，可采用“重采样”（re-sampling）避免训练过程过早停止；即抛弃当前不满足条件的基分类器，基于重新采样的数据训练分类器，从而获得学习“重启动”机会。

AdaBoost能够自适应（addaptive）地调整样本的权值分布，将分错的样本的权重设高、分对的样本的权重设低；所以被称为“Adaptive Boosting”。

sklearn的AdaBoostClassifier实现了AdaBoost，默认的基分类器是能fit()带权值样本的DecisionTreeClassifier。

下面是${\alpha }_m$和$G_m (x) $的推导过程，不喜欢的可以直接跳过去

---

损失函数已知为下面的公式
$$L(y,f(x))=\frac{1}{n}\sum _{i=1}^{n}exp(-y_{i}f(x_i))$$

我们的目标是求使得到的${\alpha }_m$和$G_m(x)$令$L(y,f(x))$最小，即：

$$\begin{gathered} ({\alpha }_m,G_m(x))=\underset{{\alpha }_m,G_m}{argmin}\sum _{i=1}^n{e}^{-y_i(f_{m-1}(x)+{\alpha }_m{G}_m(x))} \\ =\underset{{\alpha }_m,G_m}{argmin}\sum _{i=1}^n{\bar{w}}_{mi}{e}^{-y_i{\alpha }_m{G}_m(x)} \\ {G}_m(x{)}^{\ast }=\underset{G_m(x)}{argmin}\sum _{i=1}^n{\bar{w}}_{mi}I(y_i\ne G_m(x)) \end{gathered}$$

其中，${\bar{w}}_{mi}=e^{-y_i{f}_{m-1}(x)}$。因为${\bar{w}}_{mi}$既不依赖于${\alpha }_m$也不依赖于$G_m(x)$，所以与最小化无关。但它依赖于$f_{m-1}(x)$，会随着每一轮迭代而发生变化。第二个式子为令指数损失函数最小的$G_m(x)\ast$，其中$I(\cdot )$为指示函数，此$G_m(x)\ast$使第$m$轮加权训练数据分类的误差率得到了最小值。接下来我们对上边的第一个式子的右边进行一下简单变形：

$$\begin{gathered} \sum _{i=1}^n{\bar{w}}_{mi}{e}^{y_i{\alpha }_t{G}_t(x_i)} \\ =\sum _{y_i=G_t(x_i)}{\bar{w}}_{mi}{e}^{-{\alpha }_m}+\sum _{y_i\ne G_m(x_i)}{\bar{w}}_{mi}{e}^{{\alpha }_m} \\ =(e^{{\alpha }_m}-e^{-{\alpha }_m})\sum _{i=1}^n{\bar{w}}_{mi}I(y_i\ne G_m(x_i))+e^{-{\alpha }_m}\sum _{i=1}^n{\bar{w}}_{mi} \end{gathered}$$

将上式对${\alpha }_m$求导并令导数为0，即可解得：
$${\alpha }_m^{\ast }=\frac{1}{2}log\frac{1-e_m}{e_m}$$

上式即之前例子中所用到的${\alpha }_m$的更新公式，其中，$e_m$为分类误差率：

$$\begin{gathered} e_m=\frac{{\sum }_{i=1}^n{\bar{w}}_{mi}I(y_i\ne G_m(x_i))}{{\sum }_{i=1}^n{\bar{w}}_{mi}} \\ =\sum _{i=1}^n{w}_{mi}I(y_i\ne G_m(x_i)) \end{gathered}$$

---

算法案例代码实现：

https://github.com/626626cdllp/data-mining/tree/master/ensemble-learning/adaboost

GBDT梯度提升决策树

详情参考：https://blog.csdn.net/luanpeng825485697/article/details/79766455

gbdt全称梯度下降树，在传统机器学习算法里面是对真实分布拟合的最好的几种算法之一。

GBDT(Gradient Boosting Decision Tree) 又叫 MART（Multiple Additive Regression Tree)，是一种迭代的决策树算法，该算法由多棵决策树组成，所有树的结论累加起来做最终答案。它在被提出之初就和SVM一起被认为是泛化能力较强的算法。

GBDT中的树是回归树（不是分类树），GBDT用来做回归预测，调整后也可以用于分类。

回归树可以参考http://blog.csdn.net/luanpeng825485697/article/details/78795504

提升树利用加法模型和前向分步算法实现学习的优化过程。当损失函数是平方损失和指数损失函数时，每一步的优化很简单，如平方损失函数学习残差回归树。

但对于一般的损失函数，往往每一步优化没那么容易，如绝对值损失函数和Huber损失函数。针对这一问题，Freidman提出了梯度提升算法：利用最速下降的近似方法，即利用损失函数的负梯度在当前模型的值，作为回归问题中提升树算法的残差的近似值，拟合一个回归树。

所以说GBDT是通过采用加法模型（即基函数的线性组合），以及不断减小训练过程产生的残差来达到将数据分类或者回归的算法。

算法步骤解释：

1、初始化，估计使损失函数极小化的常数值，它是只有一个根节点的树，即ganma是一个常数值。
2、
（a）计算损失函数的负梯度在当前模型的值，将它作为残差的估计
（b）估计回归树叶节点区域，以拟合残差的近似值
（c）利用线性搜索估计叶节点区域的值，使损失函数极小化
（d）更新回归树
3、得到输出的最终模型 f(x)

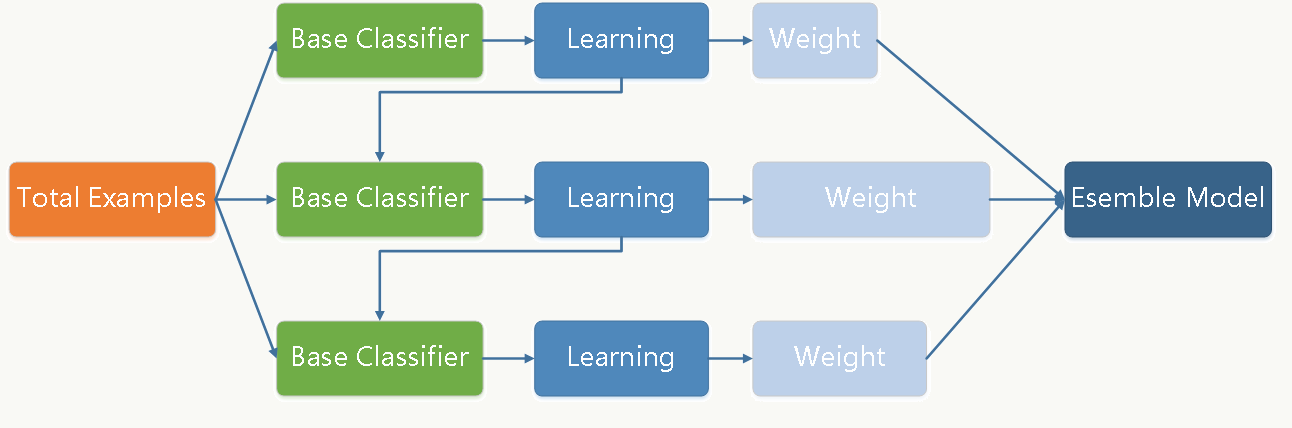
GBDT通过多轮迭代,每轮迭代产生一个弱分类器，每个分类器在上一轮分类器的残差基础上进行训练。对弱分类器的要求一般是足够简单，并且是低方差和高偏差的。因为训练的过程是通过降低偏差来不断提高最终分类器的精度。

弱分类器一般会选择为CART 树（也就是分类回归树）。由于上述高偏差和简单的要求 每个分类回归树的深度不会很深。最终的总分类器 是将每轮训练得到的弱分类器加权求和得到的（也就是加法模型）。

xgboost

详情参考：https://blog.csdn.net/luanpeng825485697/article/details/79766455

如果不考虑工程实现、解决问题上的一些差异，xgboost与gbdt比较大的不同就是目标函数的定义。

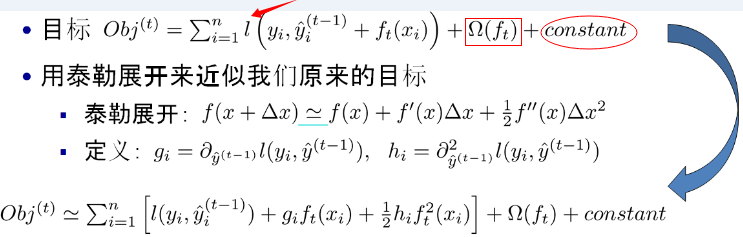
注：红色箭头指向的l即为损失函数；红色方框为正则项，包括L1、L2；红色圆圈为常数项。xgboost利用泰勒展开三项，做一个近似，我们可以很清晰地看到，最终的目标函数只依赖于每个数据点的在误差函数上的一阶导数和二阶导数。

模型融合：bagging、Boosting、Blending、Stacking

上面我们已经学习了集成学习的Bagging、Boosting，下面我们来看看还有那些模型融合方法。

常见的 Ensemble 方法有这么几种：
1、Bagging：使用训练数据的不同随机子集来训练每个 Base Model，最后进行每个 Base Model 权重相同的 Vote。也即 Random Forest 的原理。
2、Boosting：迭代地训练 Base Model，每次根据上一个迭代中预测错误的情况修改训练样本的权重。也即 Gradient Boosting，Adaboost 的原理。比 Bagging 效果好，但更容易 Overfit。
3、Blending：用不相交的数据训练不同的 Base Model，将它们的输出取（加权）平均。实现简单，但对训练数据利用少了。
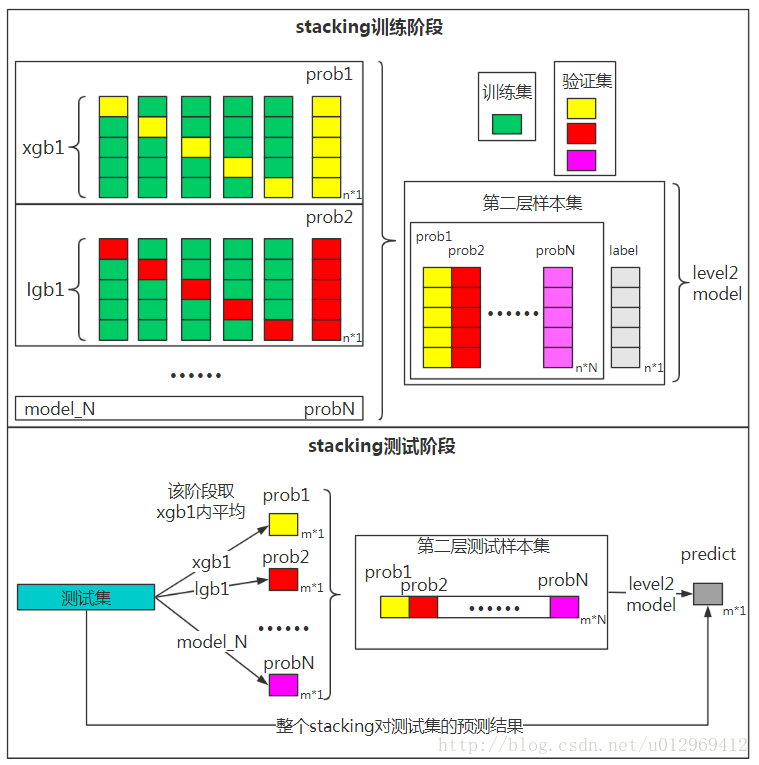
4、Stacking：

还有一种是将prob1~N列与原始数据组成新的特征向量（样本集列数+N）训练LV2模型