傅里叶级数

UTF8gbsn

Introduction

首先我们来看看傅里叶级数在做一个什么样的事情。针对的对象是什么，目的是什么。

• 傅里叶级数针对的对象有两个。(其中，关于收敛性质的一些条件限制，本文暂不
  讨论，主要是为了简单问题。让读者有一个更为清晰的骨架认识。细节部分就像是皮肉，
  可以让知识更加丰满。还需要读者去阅读更为详细的材料。但是有了骨架我相信阅读起
  来就会更为简单和顺畅。)

  • 周期函数，比如$sin(2x)+cos(3x)$

  • 非周期函数，但是定义在某个区间上。比如 $$f(x)=\{\begin{array}{rl}& x^2,0⩽x⩽2\\ & 0,\end{array}$$

    对于这样的函数，我们可以做周期延拓，让他成为一个周期函数。

  

  而且，我们可以进行周期扩展把任何周期函数的周期变换为$2\pi$,只需要加一个缩
  放因子就好了。所以后面我们讨论的范围只针对周期为$2\pi$，的函数也不会失去一
  般性.

• 我们再来看傅里叶级数的目的。傅里叶级数的目的是将目标函数$f(x)$展开为一个，
  正弦和余弦的函数的级数。也就是
  $$f(x)=\frac{a_0}{2}+\sum _{n=1}^{\infty }(a_{n}cos(nx)+b_{n}sin(nx))$$
  其中，$a_n,b_n$是什么东西？
  $$a_n=\frac{1}{\pi }{\int }_{-\pi }^{\pi }f(x)cos(nx)dx,(n=0,1,2,...)$$

  $$b_n=\frac{1}{\pi }{\int }_{-\pi }^{\pi }f(x)sin(nx)dx,(n=0,1,2,...)$$

  暂时看不明白这个式子不要紧。我们会慢慢展开，从一个比较直观的角度来理解这个级
  数的意义。

Time and Frequency

时间和频率的关系和变换是理解傅里叶级数的关键。如果读者忽略了时间和频率的转换关
系。那么读者将不会真正理解傅里叶级数，进而影响到以后会谈到的傅里叶变换。让我们
来仔细看看，傅里叶级数在干一件什么事情。

1. 傅里叶级数的目标函数是定义在时间域上的。也就是说，傅里叶级数的目标函数
   是时变的$f(t)$.

2. 傅里叶级数的生成级数是不同频域信号在时域上的叠加。我们后面会看到是怎么回
   事。

让我们具体看看一看傅里叶级数的主题是什么。

• 有人提出一种展开方式(傅里叶级数)，可以展开呢定义在$(-\infty ,\infty )$上周期为$2\pi$的
  函数$f(x)$。

• 然后有人又证明了这个展开式(傅里叶级数)，在有些条件下收敛,且收敛于$f(x)$。

通过这两点，我们就把一个时间域的信号。用多个不同频率的信号叠加生成了。

From Bottom Up

我们来看看自低想上来分析傅里叶级数，的物理意义。

Orthodox Sin and Cos

首先我们来理解一个非常重要的概念叫做正交三角函数

$$\begin{array}{rl}& {\int }_{-\pi }^{\pi }cos(nx)dx,(n=,1,2,3,...)\\ & {\int }_{-\pi }^{\pi }sin(nx)dx,(n=,1,2,3,...)\\ & {\int }_{-\pi }^{\pi }cos(kx)sin(nx)dx,(n,k=,1,2,3,...)\\ & {\int }_{-\pi }^{\pi }cos(kx)cos(nx)dx,(n,k=,1,2,3,...)\\ & {\int }_{-\pi }^{\pi }sin(kx)sin(nx)dx,(n,k=,1,2,3,...)\end{array}$$

也就是说

$$1,cos(x),sin(x),cos(2x),sin(2x),\cdots$$

之间互相正交。他们两两之间的乘积的积分在$(-\pi ,\pi )$上是0。

Time Function Map

我们来看看时域的函数，$f(t)$的展开式,注意我们现在只是定义了一个这样的展开式。但
是并未去证明它的收敛性质。我们把符号$=$换成一个符号$\mapsto$。这个展开式就是傅
里叶级数，但是我们并没有去证明它收敛和相等。我们暂时只是把收敛定理写在这里，不
做证明。如果需要请参考相应的资料。或者后面另写专题来证明傅里叶级数的收敛性证明

**定理:**设$f(x)$是周期为$2\pi$的周期函数，如果它满足

• 在一个周期内连续或只有有限个第一类间断点。

• 在一个周期内至多只有有限个极值点

则$f(x)$的傅里叶级数收敛，并且当$x$是连续点是，收敛于$f(x)$,而当x是间断点时,收
敛于$\frac{1}{2}[f(x^{-})+f(x^{+})]$ 。

当然这个定理，可以把它当做既定事实。我们就可以接下来看傅里叶级数的具体计算。

$$f(t)\mapsto A_0+\sum _{n=1}^{\infty }{A}_{n}sin(n\omega t+{\phi }_n)$$

根据

$$A_{n}sin(n\omega t+{\phi }_n)=A_{n}sin({\phi }_n)cos(n\omega t)+A_{n}cos({\phi }_n)sin(n\omega t)$$

然后我们令

$$\{\begin{array}{rl}\frac{a_0}{2}=& A_0\\ a_n=& A_{n}sin({\phi }_n)\\ b_n=& A_{n}cos({\phi }_n)\\ \omega =& \frac{\pi }{l},(T=2l)\end{array}$$

那么

$$f(t)\mapsto \frac{a_0}{2}+\sum _{n=1}^{\infty }[a_{n}cos(\frac{n\pi t}{l})+b_{n}sin(\frac{n\pi t}{l})]$$

我们实际上把周期为$2l$的映射变换为了周期为$2\pi$的映射.我们再让
$x=\frac{t\pi }{l}$可得

$$f(t)\mapsto \frac{a_0}{2}+\sum _{n=1}^{\infty }[a_{n}cos(nx)+b_{n}sin(nx)]$$
我们来看看变换的具体变量.

• 原函数为$f(t)$，是定义在$-l,l$上的周期函数，也就是说$l\in (-l,l)$.

• 我们来看看我们映射后的变量是$x\in (-\pi ,\pi )$,其实这还是一个时域的变量。

• 那么问题来了，那频域去哪里了。那么我们来看一个具体的例子来。比如函数
  $f(t)=3+3sin(t)+5sin(2t)+6cos(3t)$.禁果傅里叶变换后，为
  $$f(t)=3+3sin(t)+5sin(2t)+6cos(3t)$$
  (感谢rrii指出的错误.)
  也就是说，这个函数被变换到了由3个不同频域的函数叠加而成。这里我们使用的本来就是一个由正弦余弦构成的函数.自然很容易看出频域成分.但是如果时一个更为复杂的函数,就没那么容易了.但是你可以使用傅里叶变换,它能够帮你分析出里面的频域成分.这也是傅里叶变换重要的作用
  $T=2\pi ,T=\pi ,T=\frac{2\pi }{3}$

• 换言之，这三个频率的函数组合起来,
  就原来的函数$f(t)$。下面的频域函数和
  $f(t)$是等价关系，也就是通过一个函数可以计算另一个函数。
  

这里还要着重强调的一点事，傅里叶级数展开的频率是一定的。也就是说分别展开为周期
为
$$\frac{2\pi }{1},\frac{2\pi }{2},\frac{2\pi }{3},...,\frac{2\pi }{n},(n=,1,2,3,....)$$

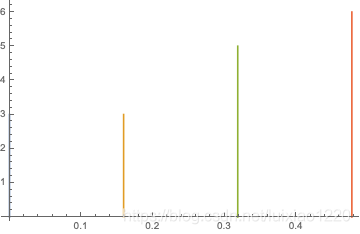
注意傅里叶级数是没有频率,比如$\frac{3\pi }{2}$的频率成分的。只有上面提到的评率
成分。而和傅里叶变换不同的地方正式在这里。傅里叶变换的频率成分是连续的。不是如
上面的式子显示的那样是离散的。

Get parameters

让我们来看看如何求$a_0,a_k,b_k$

$${\int }_{-\pi }^{\pi }f(x)dx={\int }_{-\pi }^{\pi }\frac{a_0}{2}dx+\sum _{k=1}^{\infty }[a_k{\int }_{-\pi }^{\pi }cos(kx)dx+b_k{\int }_{-\pi }^{\pi }sin(kx)dx]$$

回想一下正交正弦余弦的定义。我们可以得出等式为

$${\int }_{-\pi }^{\pi }f(x)dx=\frac{a_0}{2}\cdot 2\pi \Rightarrow a_0=\frac{1}{\pi }{\int }_{-\pi }^{\pi }f(x)dx$$

再来看等式

$${\int }_{-\pi }^{\pi }f(x)cos(nx)dx$$

$$\frac{a_0}{2}{\int }_{-\pi }^{\pi }cos(nx)dx+\sum _{k=1}^{\infty }[a_k{\int }_{-\pi }^{\pi }cos(kx)cos(nx)dx+b_k{\int }_{-\pi }^{\pi }sin(kx)cos(nx)dx]$$

根据正交的性质，我们可以得到（正交的概念一定要理解清楚，这是计算$a_n,b_n,a_0$）
的关键

$$a_n=\frac{1}{\pi }{\int }_{-\pi }^{\pi }f(x)cos(nx)dx$$
$$b_n=\frac{1}{\pi }{\int }_{-\pi }^{\pi }f(x)sin(nx)dx$$

于是我们能求出所有的傅里叶级数

$$f(x)=\frac{a_0}{2}+\sum _{n=1}^{\infty }(a_{n}cos(nx)+b_{n}sin(nx))$$

The End

傅里叶级数，就是把一个周期的时域信号，分解为，不同频率的信号的叠加。注意这些频率
不是连续的而是离散的。因为$n=1,2,3,...$.这个和傅里叶变换最关键的不同之处。后面我
们会来谈谈傅里叶变换。傅里叶变换的理解，可以从傅里叶级数中来找到灵感了思路。

我们要强调一点：傅里叶级数的收敛性质我们没有证明，这不影响工程上应用傅
里叶级数。我们只是陈述一点，也就是只要满足一定条件的周期函数。就可以展开为傅里叶
级数。而系数的计算则是上一节给出来的。