LeetCode 11. 盛最多水的容器,【难度:中等;通过率:59.8%】,这道题的精髓在于 木桶效应的巧妙应用,通过双指针算法实现 O(n) 时间复杂度的最优解
一、题目描述
给定一个长度为 n 的整数数组 height。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i])。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明:你不能倾斜容器
示例:
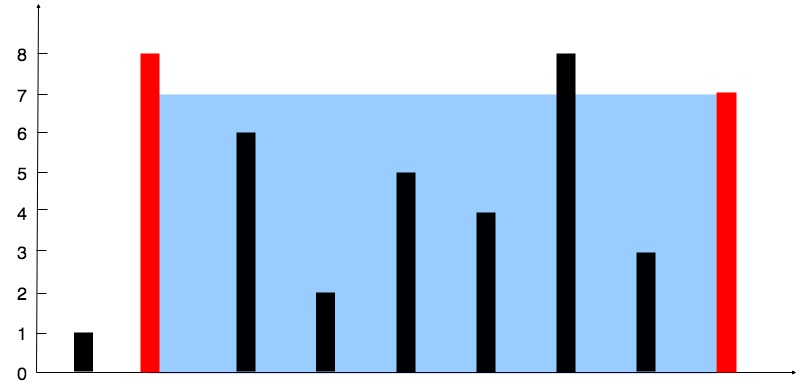
输入: nums = [1,8,6,2,5,4,8,3,7]
输出: 49
解释: 图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
二、木桶效应的启发
题目的要求是找到能容纳最多水的容器。直接暴力枚举所有可能的组合会比较复杂,时间复杂度为O(n²)。这里有一个非常关键的思想转换:
如果我们将容器看作一个木桶,那么容器能装多少水就取决于最短的那块木板,而不是最长的。
- 容器的宽度 = 两条线之间的距离
(r - l) - 容器的高度 = 两条线中较短的那条
min(height[l], height[r]) - 容器的容量 = 宽度 × 高度 =
(r - l) * min(height[l], height[r])
通过这个转换,问题就从"找到能容纳最多水的容器",变成了"如何高效地找到最优的左右边界组合",涉及到“左右”的遍历,自然而然想到双指针的具体实现
当然,木桶效应只是一个灵感,实际上可行的原因,是对底层的局部最优解的洞察,详见下文
三、双指针解法
现在问题是如何高效地找到最优的左右边界组合。显然,暴力枚举所有可能的组合需要 O(n²) 时间复杂度,这在数据量大的情况下显然超时
双指针算法的核心思想:
- 初始化:左指针
l指向数组开头,右指针r指向数组末尾 - 贪心策略:每次移动较短的那一端
- 为什么移动短板?
- 如果移动长板,宽度减少,高度不变或减少,容量必然不会增加(即贪心的思想,寻求局部最优)
- 如果移动短板,虽然宽度减少,但高度可能增加,容量有可能增加
- 终止条件:两个指针相遇
关键洞察:移动长板永远不会得到更大的容量,因此移动短板是唯一可能改善结果的选择。这个贪心策略保证了我们不会错过最优解
四、代码实现
这就是我们将上述所有思路融合在一起的最终代码:
class Solution {
public int maxArea(int[] height) {
// 1. 初始化双指针:左指针指向数组开头,右指针指向数组末尾
int l = 0, r = height.length - 1;
int ans = Integer.MIN_VALUE; // 记录最大容量
// 2. 双指针向中间收缩,直到相遇
while (l < r) {
// 3. 根据木桶效应,容量由较短的板决定
if (height[l] < height[r]) {
// a. 左板较短,计算当前容量并更新最大值
// 容量 = 宽度 × 高度 = (r - l) × height[l]
ans = Math.max(ans, (r - l) * height[l]);
// b. 移动左指针,寻找可能更高的左板
// 因为右板更高,移动右板不可能得到更大容量
l++;
} else {
// a. 右板较短或相等,计算当前容量并更新最大值
ans = Math.max(ans, (r - l) * height[r]);
// b. 移动右指针,寻找可能更高的右板
// 因为左板更高或相等,移动左板不可能得到更大容量
r--;
}
}
return ans;
}
}
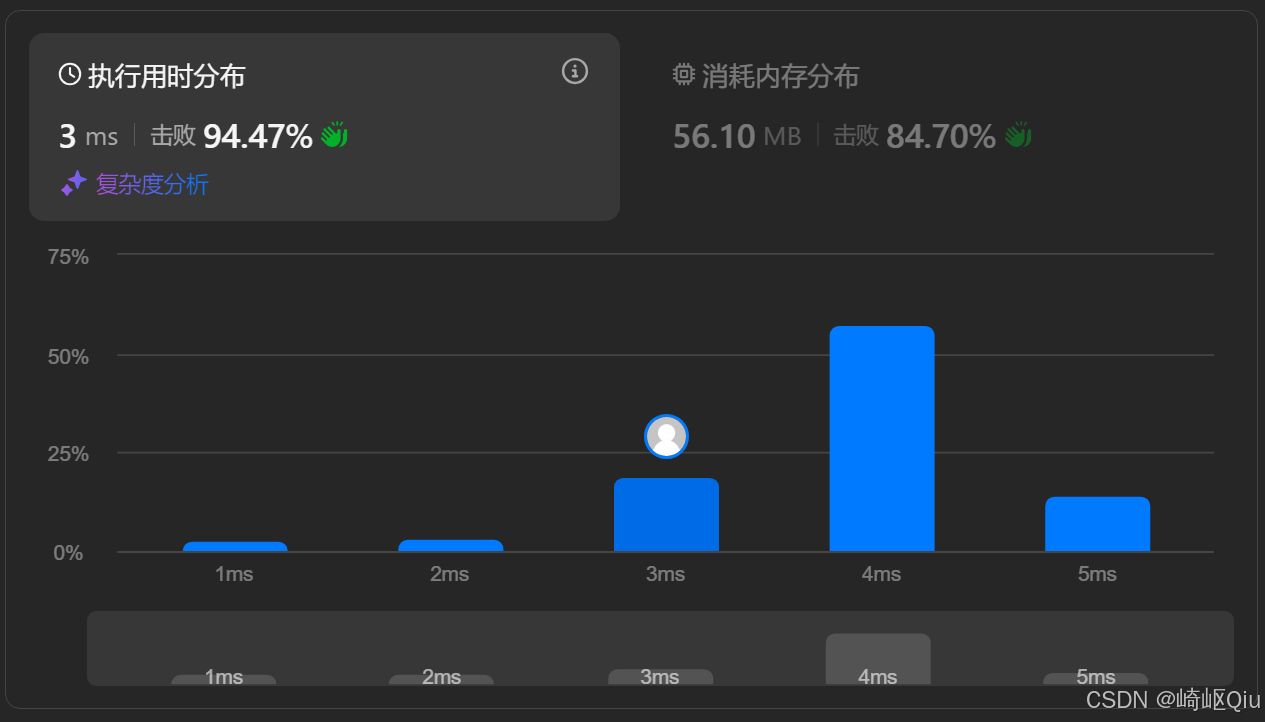
这里有一个细节:如果将 ans 的计算,放在 if-else 内部,能够相较于放在 if 外部:ans = Math.max(ans, (r - l) * Math.min(height[l], height[r]));
减少一定的执行时间,由 5ms 到 3ms
提交结果:
五、关键点与复杂度分析
- 思想转换:将"容器容量最大化"问题转化为"木桶效应"问题是解题的一种灵感
- 双指针 + 贪心策略:这是解决各类边界优化问题的标准、高效模式
- 正确性保证:移动长板永远不会得到更优解,这是算法正确性的底层逻辑
- 时间复杂度:O(N) 我们只需要对数组进行一次遍历,每个元素最多被访问一次
- 空间复杂度:O(1) 只使用了常数级别的额外空间,没有使用递归或额外的数据结构
算法对比
| 方法 | 时间复杂度 | 空间复杂度 | 优缺点 |
|---|---|---|---|
| 暴力枚举 | O(n²) | O(1)或者O(n) | 思路简单直观,但效率低下 |
| 双指针 | O(n) | O(1) | 高效优雅,是最优解 |






















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








