一、指数哥伦布编码映射关系
指数哥伦布码是一种压缩编码算法。指数哥伦布编码有四种映射关系,从k到code_num,其中,code_num是码字的编号:
ue:无符号整数指数哥伦布编码的语法元素,这种映射关系应用在宏快类型、参考帧索引等。映射关系为:code_num=k;
se:有符号整数指数哥伦布编码的语法元素,左位在先,这种映射关系应用在运动矢量插值、量化参数插值等。
映射关系为:code_num=2|k| (k <= 0)
code_num=2|k|-1 (k > 0)
te:舍位指数哥伦布编码的语法元素;
me:映射的指数哥伦布编码的语法元素,左位在先。参数k通过指定的表格映射到code_num。这种映射关系应用于coded_block_parttern参数。
每种映射关系被设计成对出现频率高的值使用较短的码字,对出现频率低的值使用较长的码字。
二、指数哥伦布编码的逻辑结构
指数哥伦布编码的逻辑结构为:[M Zeros] [1] [INFO],包括前缀码和信息位两个部分。其中,INFO是M个bit所携带的信息。例如,如下码字:
code_num codeword code_num codeword
0 1 4 00101
1 010 5 00110
2 011 6 00111
3 00100 7 0001000
codeword 0 没有前缀码和INFO,codeword 1 和 2 有1 bitINFO,codeword 3到6有两 bit INFO。每个哥伦布码字的长度为2M+1,并且基于code_num,每个codeword可以被重构,通过下面的公式:
M = floor[log2(code_num + 1)]
INFO = code_num + 1 - 2^M
一个codeword可以通过下面的方式来解码:
(1)读入M个bit的前缀0,紧接着是1;
(2)读入M个bit的INFO;
(3)code_num = 2^M + INFO -1 (对于codework 0,M和INFO都为0).
三、K阶指数哥伦布码
K阶级指数哥伦布码如下表所示,表中给出了0阶、1阶、2阶和3阶的指数哥伦布码。
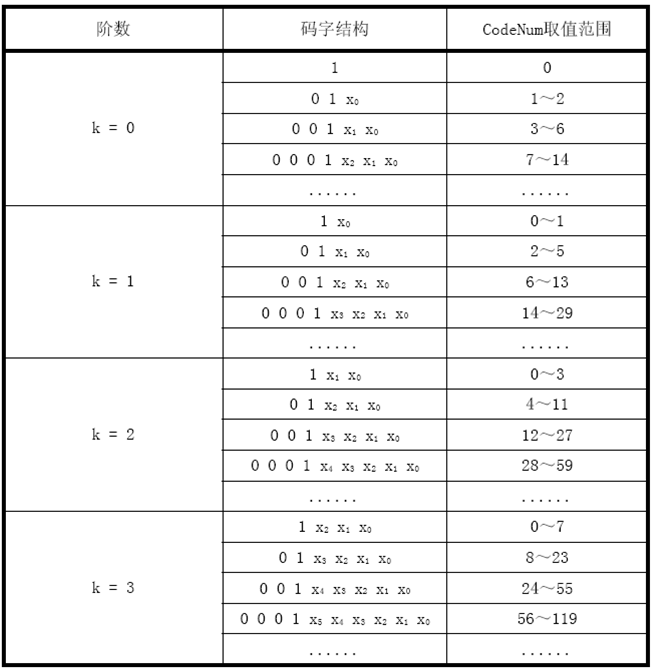
k阶哥伦布编码的逻辑结构:[(M-k) Zeros] [1] [M bits INFO]
M = floor[log2(code_num + 2^k)]
INFO = code_num + 2^k - 2^M
码字长度:L = (M - K) + 1 + M = 2 * M - K + 1
1、k阶哥伦布码的编码过程
用来表示非负整数的k阶指数哥伦布码,可以通过下面的方式获得:
(1)将数字以二进制的形式写出,去掉最低的k个比特位,然后加1;
(2)计算剩下的比特数,将此数减1,即得前缀0的个数M-k;
(3)将第一步中去掉的最低k个比特位补回比特串尾部。
2、k阶哥伦布码的解码过程
code_num = 2^(leadingZeroBits + k) - 2^k + values;
其中,values为第一个非零比特其后的(leadingZeroBits + k)个比特的值。






















 1017
1017

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








