素数筛

素数又称质数，是指除了1和它本身，再也没有其他的因子。
合数是除了1和它本身以外，还有其他的因子。
1既不是素数也不是合数。

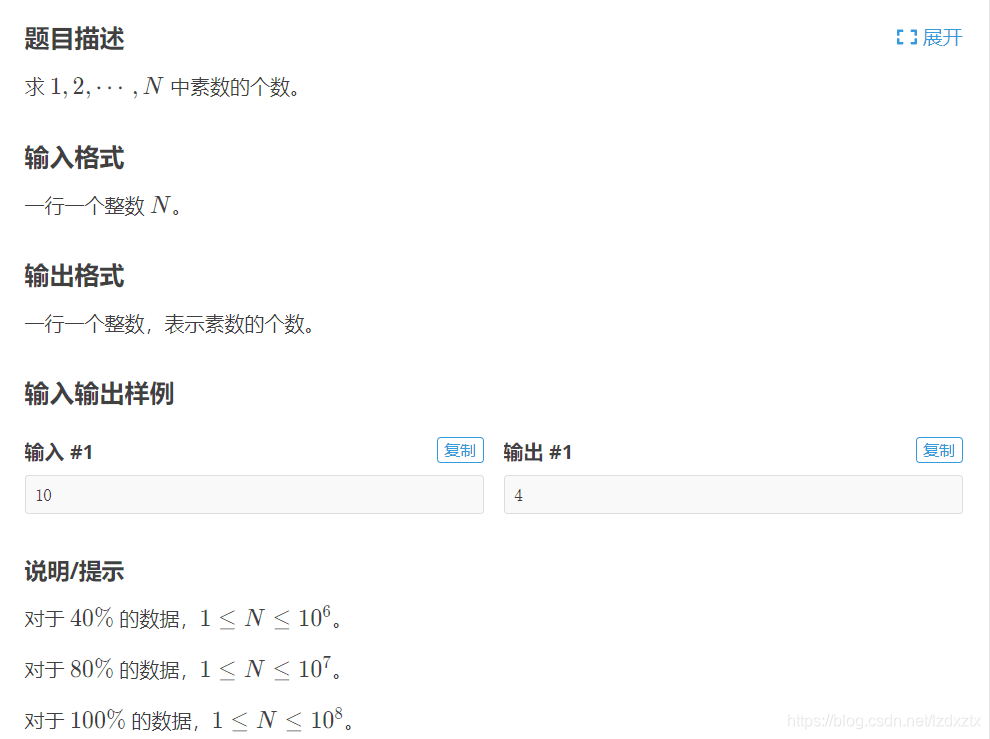
此题为洛谷上的一道题，以此题为例题，讲解素数筛。

埃氏筛法

时间复杂度O(nlogn)
得分 80

#include <iostream>
#include <cstdio>
using namespace std;
bool isprime[100000000]={true,true};//isprime[i]为false代表i为素数
int main()
{
   int n,ans=0;
   cin>>n;
   for(int i=2;i<=n;i++)//把数i的j倍全部筛掉，比如把5的2倍，3倍，4倍……全部筛掉，
   {
       if(isprime[i]==false)
       {
           ans++;
           for(int j=2;i*j<=n;j++)
            isprime[i*j]=true;
       }
   }
   cout<<ans;
}

埃氏筛的时间复杂度为nlogn，对于输入10的8次方，必然会TLE，此算法只能得80分，因为会TLE一个点。
来分析一下埃氏筛法：
此算法有重复步骤，比如当i=2的时候，4,6,8,10,12,14,16,18，都会被筛掉，但是当i=3的时候，6,9,12,15,18,21,被筛掉,6,12,18又会被筛一次，当数据比较大的时候，重复的就比较多，耗费了不必要的时间。

优化的线性筛

时间复杂度O(n)
得分 100

#include <iostream>
#include <cstdio>
using namespace std;
bool isprime[100000000]={true,true};//isprime[i]为false代表i为素数
int p[100000000];
int main()
{
   int n,cnt=0;
   cin>>n;
   for(int i=2;i<=n;i++)
   {
      if(!isprime[i])
        p[cnt++]=i;//存下所有的素数
      for(int j=0;j<cnt&&p[j]*i<=n;j++)
      {
          isprime[p[j]*i]=true;//将现有的素数的i倍都给筛掉
          if(i%p[j]==0)break;//此语句是改进的核心，读者可自行画图理解
      }
   }
   cout<<cnt;
}