快手高频面试题之计算数组小和（相关话题：归并排序，双指针）

题目描述

数组小和的定义如下：

例如，数组s=[ 1,3,5,2,4,6],在s[0]的左边小于或等于s[0]的数的和为0,在s[l]的左边 小于或等于s[l]的数的和为1,

在s[2]的左边小于或等于s[2]的数的和为1+3=4,

在s[3]的 左边小于或等于s[3]的数的和为1,

在s[4]的左边小于或等于s[4]的数的和为1+3+2=6,

在 s[5]的左边小于或等于s[5]的数的和为1+3+5+2+4=15,所以s的小和为0+1+4+1+6+15=27。

给定一个数组s,实现函数返回s的小和。

思路分析 

用时间复杂度为。(M)的方法比较简单，按照题目例子描述的求小和的方法求解即可， 本书不再详述。下面介绍一种时间复杂度为O(MoglV)、额外空间复杂度为O(N)的方法，这 是一种在归并排序的过程中，利用组间在进行合并时产生小和的过程。

1. 假设左组为l[]，右组为r[],左右两个组的组内都已经有序，现在要利用外排序合 并成一个大组，并假设当前外排序是l[i]与r[j]在进行比较。
2. 如果l[i]<=r[j],那么产生小和。假设从r[j]往右一直到r[]结束，元素的个数为m, 那么产生的小和为l[i]*m。
3. 如果l[i]>r[j]，不产生任何小和。
4. 整个归并排序的过程该怎么进行就怎么进行，排序过程没有任何变化，只是利用步 骤1〜步骤3,也就是在组间合并的过程中累加所有产生的小和，总共的累加和就是结果。 还是以题目的例子来说明计算过程。

图8-1

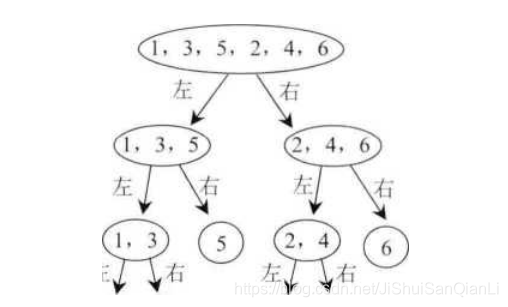
1.   归并排序的过程中会进行拆组再合并的过程。［13,5,2,4,6］拆分成左组［1,3,5］和右组 ［2,4,6］, ［1,3,5］再拆分成［1,3］和［5］, ［2,4,6］再拆分成［2,4］和［6］, ［1,3］再拆分成［1］和［3］, ［2,4］ 再拆分成［2］和［4］,如图8-1所示。
2. ［1］与［3］合并。1和3比较，左组的数小，右组从3开始到最后一共只有1个数，所 以产生小和为1x1 = 1,合并为［1,3］。
3. ［1,3］与［5］合并。1和5比较，左组的数小，右组从5开始到最后一共只有1个数， 所以产生小和为1*1=1。同理，3和5比较，产生小和为3x1=3,合并为［1,3,5］。
4. ［2］与［4］合并。2和4比较，左组的数小，右组从4开始到最后一共只有1个数，所 以产生小和为2x1=2,合并为［2,4］o
5. ［2,4］与［6］合并。与步骤3同理,产生小和为6,合并为［2,4,6］
6. ［1,3,5］与［2,4,6］合并。1和2比较，左组的数小，右组从2开始到最后一共有3个数， 所以产生小和为1x3=3。3和2比较，右组的数小，不产生小和。3和4比较，左组的数小， 右组从4开始到最后一共有2个数，所以产生小和为3x2=6。5和4比较，右组的数小，不 产生小和。5和6比较，左组的数小，右组从6开始到最后一共有1个数，所以产生小和 为 5,合并为［1,2,3,4,5,6］。

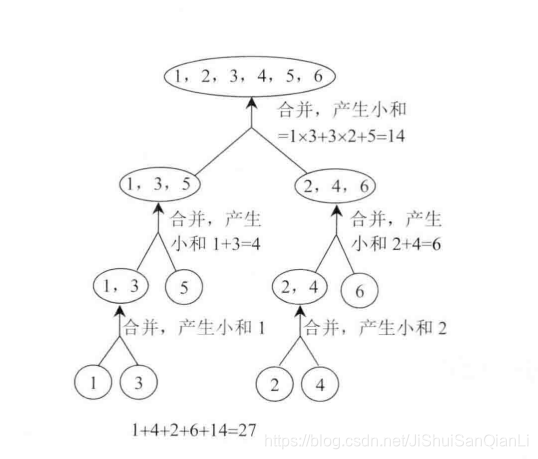
归并过程结束，总的小和为1+1+3+2+6+3+6+5=27。合并的全部过程如图8-2所示

图8-2

参考代码

package com.lzhsite.leetcode.algoritom.practise.arrays;

public class 计算数组小和 {

	public int getArrMinSum(int[] s, int left, int right) {

		int mid = (left + right) / 2;

		return getArrMinSum(s, left, mid) + getArrMinSum(s, mid + 1, right) + merge(s, left, mid, right);
	}

		public int merge(int[] s, int left, int mid, int right) {

		// tempArr保存s[left,mid]和s[mid+1,right]归并后的数据从小到大排序
		int[] tempArr = new int[right - left + 1];
		int tempIndex = 0;
		int i = left;
		int j = mid+1;

		int minSum = 0;

		/**
		 * 利用while里利用循环i,j指针这步很难想到
		 */
		while (i <= mid && j <= right) {

			if (s[i] < s[j]) {

				minSum = minSum + (right - j) * s[i];
				tempArr[tempIndex] = s[i];
				i++;
				tempIndex++;

			} else {
				tempArr[tempIndex] = s[j];
				j++;
				tempIndex++;
			}

		}

		
		//把左数组或右数组没有合并的剩余数据合并起来
		for (; i < left + 1 || j < right + 1; i++, j++) {
			tempArr[tempIndex] = i > mid ? s[j] : s[i];
			tempIndex++;
		}

		
		//把归并后的有序数组重新赋值
		for (int k = 0; k < tempArr.length; k++) {
			s[left + k] = tempArr[k];
		}

		return minSum;
	}

}

总结

while里利用循环i,j指针这步很难想到，代码要自己写出来才能算掌握

参考文章

快手为何频繁考察这道Leetcode里没有的题