形式化方法 | Proof Engineering for Predicate Logic——Coq tatics 在谓词逻辑证明中的应用

关于Coq的安装、使用及Coq tatics在命题逻辑中的应用详见：

形式化方法 | Proof Engineering in Coq——Coq tatics 在命题逻辑证明中的应用

一、谓词逻辑（也成为一阶逻辑、量化逻辑）

1、谓词

谓词是一个包含变量（谓词变量）的语句，根据这些变量的值，它可以为 True 或者 False。

2、谓词逻辑

谓词逻辑使用关系、表达式和量化扩展命题逻辑。

即，谓词逻辑允许使用包含变量的句子对更加现实的问题进行建模。

 

二、More Coq Tatics

1、Negation: tactic unfold

【使用场景】

unfold 策略将目标中的术语替换成其定义。

（1）Coq使用 ~ 表示命题的否定，我们使用 unfold not 策略可以将 ~p 转换成 p -> False。

举个栗子：证明 ~(P /\ ~P) 成立。

证明代码如下：

Theorem example_1: forall P:Prop,
    ~(P /\ ~P).
Proof.
    unfold not.
    intros.
    inversion H.
    apply H1.
    apply H0.
Qed.

分析解释如下：

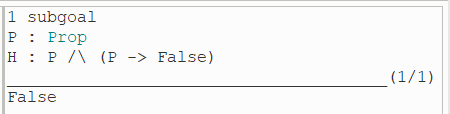
（1）观察可知，目标中包含一个全局的 ~，因此首先使用 unfold not 将这个 ~ 给展开，结果如下：

（2）然后使用 intros 拆分所要证明定理中的已知前提和所要证明的结论：

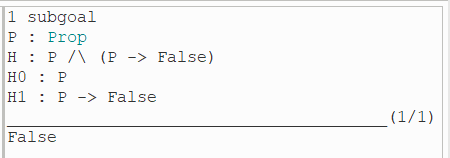
（3）已知前提 H 是一个合取式，使用 inversion 策略发现该前提 H 成立的假设：

（4）之后两次使用 apply 策略就可以证明出相应结论。

 

（2）还可以使用 unfold t in H 来展开标签为 H 的假设中 t 的定义。

 

Exercise 1: Using the tactic unfold, to prove DeMorgan law:

        ~(P \/ Q) -> ~P /\ ~Q

证明代码如下：

Theorem exercise1: forall P Q:Prop,
    ~(P \/ Q) -> ~P /\ ~Q.
Proof.
    unfold not.
    intros.
    split.
    intro H1.
    apply H.
    left.
    apply H1.
    intro H2.
    apply H.
    right.
    apply H2.
Qed.

分析解释如下：

（1）执行前五行：

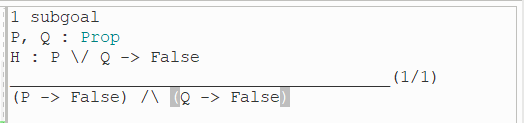
（2）发现所要证明的结论为 /\ 式，所以使用 split 策略将其分解成两个子目标：

（3）使用 intro 策略引入子目标的前提：

（4）发现第一个子目标所要证明的结论变为 False，所以直接 apply H：

（5）发现第一个子目标所要证明的结论变为 P \/ Q，而前提中包含 H1: P，所以使用 left 策略保留第一个子目标的左半部分：

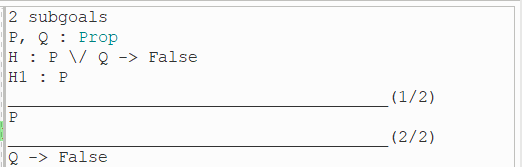
（6）apply H1 第一个子目标得证，同理可以证明第二个子目标。

 

2、Tatic assert

[使用场景】

有时我们需要从一个中间目标来证明我们当前的目标。

assert 或 assert(h：H) 策略将 H 引入为新的子目标； 证明新目标后，可以使用假设h：H证明原始目标。

举个栗子：证明 （ P /\ ~P) -> Q 成立

证明代码如下：

Theorem example_2: forall P Q:Prop,
    (P /\ ~P) -> Q.
Proof.
    unfold not.
    intros.
    assert (f: False).
    inversion H.
    apply H1.
    apply H0.
    inversion f.
Qed.

分析解释如下：

（1）执行前三行：

（2）显然，命题（P / \〜P）是错误的，因此它可以 imply 任何命题。

我们需要引入一个中间目标：（P / \〜P）是错误的。

所以引入子目标 assert(f: False)：

（3）执行4-6句证明子目标：

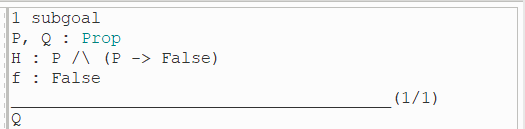
（4） 在证明了该子目标之后，我们可以将其用作新的假设来证明最初的目标：

 

3、Tactic destruct

[使用场景】

在之前的博客中，我们使用 inversion 策略打破假设中的合取或析取。

还有另一种更常用的策略来处理合取和析取：destruct 策略。

（1）假设为 /\ 式子：

该策略用两个假设P和Q代替了一个假设P / \Q。

destruct H as [H1 H2]

（2）假设为 \/ 式子：

如果该假设是析取项P \ / Q，则该策略会生成两个子目标：一个保持P，另一个保持Q。

destruct H as [H1 | H2]

（3）destruct 策略 也可以为每个归纳类型的构造函数生成子目标。

举个栗子：证明 P \/ Q -> (P -> R) -> (Q -> R) -> R 成立

证明代码如下：

Theorem example_3: forall P Q R:Prop,
    P \/ Q -> (P -> R) -> (Q -> R) -> R.
Proof.
    intros.
    destruct H as [Hp | Hq].
    apply H0 in Hp.
    apply Hp.
    apply H1 in Hq.
    apply Hq.
Qed.

（1）执行前四行：

（2）前提H为 \/ 式子，使用 destruct H as [Hp | Hq] 将其分解为两个前提：

（3）依次证明即可

 

Exercise 2: Using the tactic destruct, to prove

       P /\ (Q \/ R) <-> (P /\ Q) \/ (P /\ R).

证明代码如下：

Theorem exercise2: forall P Q R:Prop,
    P /\ (Q \/ R) <-> (P /\ Q) \/ (P /\ R).
Proof.
    intros.
    split.
    intros.
    destruct H as [Ha Hb].
    destruct Hb as [Hc | Hd].
    left.
    split.
    apply Ha.
    apply Hc.
    right.
    split.
    apply Ha.
    apply Hd.
    intros.
    destruct H as [He | Hf].
    destruct He as [Hg Hh].
    split.
    apply Hg.
    left.
    apply Hh.
    destruct Hf as[Hi Hj].
    split.
    apply Hi.
    right.
    apply Hj.
Qed.

注意点：

观察发现为双向箭头 <->，在 intros 之后使用 split 将该目标分解为两个子目标：

若要证明 P<-> Q，则需要分别证明 P-> Q 和 Q -> P。

 

三、Predicate Logic——使用 Coq 证明谓词逻辑定理

声明集合变量

Variables A B: Set.

在这里，我们声明A和B都是集合变量。

声明集合上的谓词变量

Variables P Q: A -> Prop.

可以将P和Q视为从A中获取元素并返回Prop的函数。

如果我们拥有A集合的元素，例如a：A，则可以使用P（a）表示满足属性P。

使用相同的方法，我们可以声明与多个元素相关的属性，例如，我们可以通过以下方式引入关系R，将A和B关联起来：

Variable R : A -> B -> Prop.

在此，R a b表示与a和b的关系，可以将R视为具有两个参数的函数。

1、Universal Quantification

在Coq中，关键字forall用于表示通用量化。

forall x：A, P x

表示A的所有元素都满足属性P。
 

forall x：A，P x-> Q x

表示A的任何满足属性P的元素也将满足属性Q 。

举个栗子：证明  (forall x: A, P x -> Q x) -> (forall x: A, P x) -> forall x: A, Q x. 成立

证明代码如下：

Variables A: Set.
Variables P Q: A -> Prop.
Theorem example_4:
    (forall x:A, P x -> Q x) -> (forall x:A, P x) -> forall x:A, Q x.
Proof.
    intros H1 H2 a.
    apply H1.
    apply H2.
Qed.
    

证明分析如下：

主要前提是“所有A满足特性P也满足Q”，次要前提是“所有A满足特性P”，结论是“所有A满足Q”。

（1）使用 intros 策略：

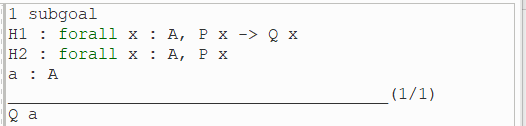
得到一个前提“ a: A”以及两个假设H1和H2。

intros a 策略引入了一个假设 a: A，则 所要证明目标中 forall 之后所有自由变量 x 都被 a 所取代。 因此，我们可以看到我们的目标变为Q a。

（2）执行 apply H1.

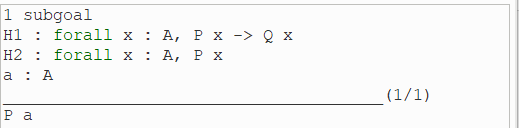
观察可知，假设H1: forall x: A, P x -> Q x，表示对于A中的所有元素，只要其满足P性质，则其一定满足Q性质，我们要证明的结论为 Q a，因此只需要能证明出 P a 即可。

因此，使用Apply H1来将假设H1实例化为Pa-> Q a。 

（3）执行 apply H2.

 

Exercise 3: Try to prove the following predicate logic proposition:

       ∀x.(~P(x) /\ Q(x)) -> ∀x.(P(x) -> Q(x))

证明代码如下：

Theorem exercise3:
    (forall x, ~P x /\ Q x) -> (forall x, P x -> Q x).
Proof.
    intros H1 a H2.
    apply H1.
Qed.

 Exercise 4: Try to prove the following predicate logic proposition:

       ∀x.(P(x) -> Q(x)) -> ∀x.~Q(x) -> ∀x.~P(x)

证明代码如下：

Theorem exercise4:
    (forall x, P x -> Q x) -> (forall x, ~Q x) -> (forall x, ~P x).
Proof.
    unfold not.
    intros H1 H2 a.
    intros.
    apply H1 in H.
    apply H2 in H.
    apply H.
Qed.

 Exercise 5: Try to prove the following predicate logic proposition:

       ∀x.(P(x) /\ Q(x)) <-> (∀x.P(x) /\ ∀x.Q(x))

证明代码如下：

Theorem exercise5:
    (forall x, (P x /\ Q x)) <-> ((forall x, P x) /\ (forall x, Q x)).
Proof.
    split.
    intros.
    split.
    apply H.
    apply H.
    intros H a.
    inversion H.
    split.
    apply H0.
    apply H1.
Qed.

 

2、Existential Quantification——使用Coq证明谓词逻辑定理

在Coq中，关键字exist用于表示存在量化。

exists x: A, P x

表示集合A中存在具有属性P的元素x。

举个栗子：证明 (exists x: A, P x) -> (forall x: A, P x -> Q x) -> exists x: A, Q x 成立。

证明代码如下：

Theorem example_5:
    (exists x:A, P x) -> (forall x:A, P x -> Q x) -> exists x:A, Q x.
Proof.
    intros H1 H2.
    destruct H1 as [a p].
    exists a.
    apply H2.
    apply p.
Qed.

分析解释如下：

（1）执行 intros H1 H2.

将前提和结论区分开。

处理已知前提和所要证明结论中的 exists 符号：

existential quantification 策略 与 conjuction(合取) 策略 类似，为了证明 exsit x:A, Q x，我们假设满足该 existence 的 x 是 a，并且将 Q 中所有的 x 都替换为 a。

在该定理中，假设 H1: exists x: A, P x   ，我们可以使用 destruct 策略将其分解为两个假设 a: A 和 P a。

（2）执行 destruct H1 as [a p].    ——假设中  exists 的消除

（3）执行 exists a.    ——目标中 exists 的消除

exists a 策略将目标中所有自由的 x 都替换为 a。

（4）执行 apply H2.

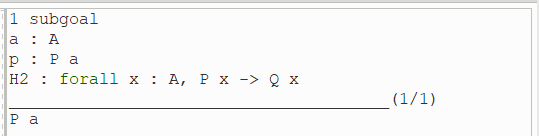
(5）执行 apply p.

 

Challenge: Try to prove the following predicate logic proposition:

       ∃x.∃y.P(x, y) -> ∃y.∃x.P(x, y)

实现代码如下：

Variables A B: Set.
Variables P: A -> B -> Prop.

(* Challenge: Try to prove the following predicate logic proposition:
       ∃x.∃y.P(x, y) -> ∃y.∃x.P(x, y) *)
Theorem challenge1:
    (exists x, exists y, P x y) -> (exists y, exists x, P x y).
Proof.
    intros.
    destruct H as [a p1].
    destruct p1 as [b p2].
    exists b, a.
    apply p2.
Qed.

 

3、tactic rewrite

【使用场景】

设项 e 的类型为 ∀(x1: T1)(x2: T2)...(xn: Tn), a=b

对于目标 P a，使用 rewrite e 可以将目标修改为 Pb，即该策略将目标里所有的a替换成b。

也可以改写假设：rewrite e in H.

反向改写规则：rewrite <- e.

举个栗子：

Theorem eq_sym' : forall(A:Type)(a b:A), a=b->b=a.
Proof.
  intros.
  rewrite H.
  reflexivity.
Qed.

分析解释如下：

（1）执行前三行：

（2）执行rewrite H. 

将所要证明结论中的b替换为a。

（3）执行 reflexivity.

当结论显然可证时，可以执行 reflexivity.

 

Challenge: Try to prove the following predicate logic proposition:

      P(b) /\ (∀x.∀y.(P(x) /\ P(y) -> x = y)) -> (∀x.(P(x) <-> x = b))

实现代码如下：

Variables A: Set.
Variables P: A -> Prop.
Variables b: A.

Theorem Challenge2:
    (P b) /\ (forall (x:A) (y:A), (P x /\ P y -> x = y)) -> (forall (x:A), (P x <-> x = b)).
Proof.
    intros.
    split.
    inversion H.
    intros.
    apply H1.
    split.
    apply H2.
    apply H0.
    intros.
    inversion H.
    rewrite H0.
    apply H1.
Qed.

 

参考：

https://www.cnblogs.com/luluathena/archive/2010/08/19/1803111.html

https://www.cnblogs.com/luluathena/archive/2010/08/19/1803111.html