一、模型的量化-nf4和pf4
由于大模型的参数量巨大,在解码阶段需要占用大量的显存资源,因而在实
际应用中的部署代价非常高。在本章中,我们将介绍一种常用的模型压缩方法,即模型量化(Model Quantization),来减少大模型的显存占用,从而使得能够在资源有限的环境下使用大模型。
例如:
from transformers import AutoModelForCausalLM
# 导入HuggingFace的tokenizer自动加载类,用于处理文本分词
from transformers import AutoTokenizer
# 导入量化配置类,用于模型参数的4位/8位量化
from transformers import BitsAndBytesConfig
# 导入PyTorch深度学习框架
import torch
# 创建4位量化配置对象
quantization_config = BitsAndBytesConfig(
# 启用4位量化加载,将模型参数压缩为4位存储
load_in_4bit=True,
# 设置4位量化的计算数据类型为float16,提升计算效率
bnb_4bit_compute_dtype=torch.float16,
# 指定使用NF4(4-bit NormalFloat)量化类型,这是最有效的4位量化方案
bnb_4bit_quant_type="nf4",
# 启用双重量化,对量化参数进行二次压缩以进一步减少内存占用
bnb_4bit_use_double_quant=True,
)
# 加载因果语言模型
model = AutoModelForCausalLM.from_pretrained(
# 指定模型名称或路径,此处为微软Phi-3-mini模型的4k上下文指令微调版本
"microsoft\Phi-3-mini-4k-instruct",
# 自动将模型分配到CUDA设备(GPU)
device_map="cuda",
# 自动推断模型参数的数据类型
torch_dtype="auto",
# 应用之前定义的4位量化配置
quantization_config=quantization_config,
# 不信任远程代码(安全设置)
trust_remote_code=False,
)
# 加载与模型匹配的tokenizer
tokenizer = AutoTokenizer.from_pretrained(
# 指定tokenizer名称或路径,与模型保持一致
"microsoft/Phi-3-mini-4k-instruct"
)
这个 BitsAndBytesConfig是 Hugging Face transformers库提供的 4-bit 量化配置,用于在加载大模型时减少显存占用。其中参数bnb_4bit_quant_type=可以取值nf4和pf4。因此次详细了解一下。
不同量化方式的对比
| 量化方式 | 显存占用 | 推理速度 | 适用场景 |
|---|---|---|---|
| FP32(全精度) | 最高 | 最慢 | 训练 / 高精度推理 |
| FP16/BF16(半精度) | 减少 50% | 较快 | 训练 / 高精度推理 |
| 8-bit 量化 | 减少 ~75% | 较快 | 低显存推理 |
| 4-bit 量化 | 减少 ~90% | 稍慢 | 极低显存推理 |
| 在量化技术中,NF4(4-bit NormalFloat) 和 FP4(4-bit Float) 是两种不同的 4-bit 量化方法,用于将模型权重从高精度(如 FP32)压缩到低比特表示(4-bit),从而大幅减少显存占用。它们的核心区别在于数值分布的处理方式。 |
1. NF4(4-bit NormalFloat)
1.1特点
• 基于正态分布优化:假设神经网络权重近似服从正态分布(大部分值集中在均值附近,两端较少),并针对这种分布设计量化区间。
• 非均匀量化:不同区间的量化步长(step size)不同,对重要范围(靠近均值)分配更多量化级别,边缘区域分配较少。
• Hugging Face 推荐:在 BitsAndBytesConfig 中默认使用 nf4,因为它在大多数 LLM 上表现更好。
1.2工作原理
- 统计权重分布:计算权重的均值和标准差,拟合正态分布。
- 设计量化区间:
• 靠近均值的区域(高概率密度)分配更多 4-bit 编码(更精细)。
• 远离均值的区域(低概率密度)分配较少编码(更粗糙)。 - 映射到 4-bit 值(16 个可能的数值)。
1.3 python实现
1.3.1. NF4(4-bit归一化浮点)实现原理
核心思想
非均匀量化 + 统计分布匹配,用4-bit(16个值)覆盖神经网络权重的典型高斯分布。
关键步骤
1.3.1.1 预定义量化值
# QLoRA论文中的NF4量化值
nf4_values = [
-1.0, -0.696, -0.525, -0.395, -0.284,
-0.185, -0.091, 0.0, 0.080, 0.161,
0.246, 0.338, 0.441, 0.563, 0.723, 1.0
]
nf4_values生成方法:
这些值是通过对海量权重数据计算分位数量化(Quantile Quantization)得到的:
•步骤1:统计海量神经网络权重的分布(通常近似N(0, σ²))
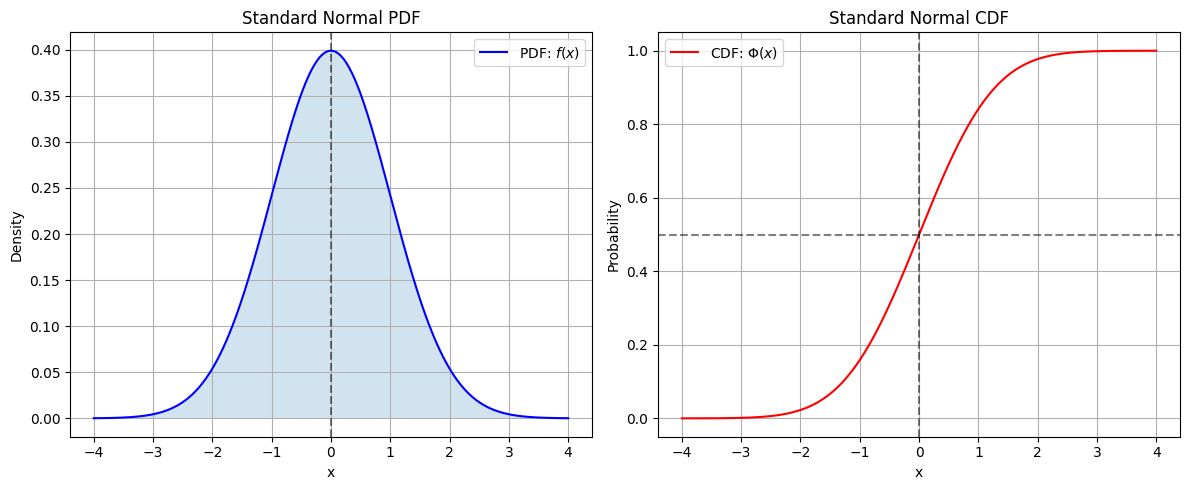
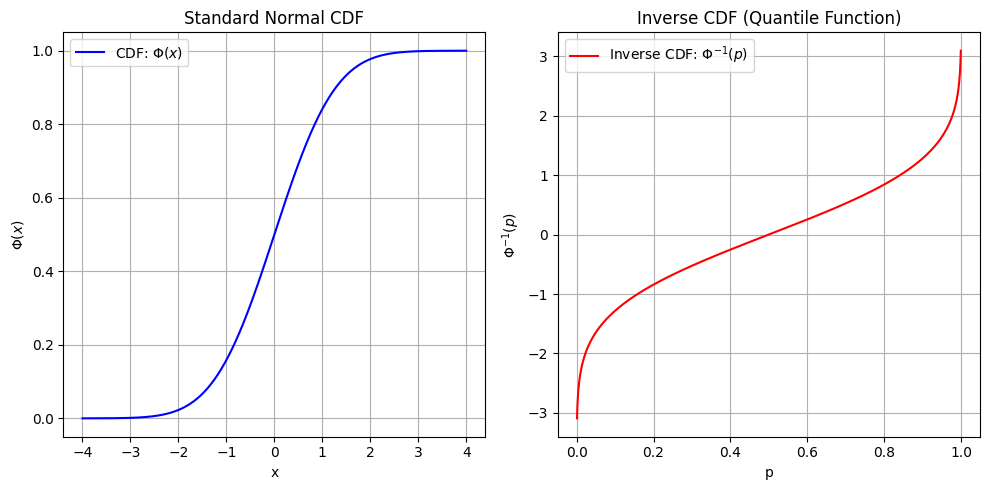
•步骤2:在**累积分布函数(CDF)**上取16个等间隔分位点i:
vi=F−1(i15),i=0,1,...,15v_i = F^{-1}\left(\frac{i}{15}\right), \quad i=0,1,...,15vi=F−1(15i),i=0,1,...,15
其中F−1F^{-1}F−1是标准正态分布的反函数(右下角图)。
1.3.1.2 最近邻搜索
def encode(x):
return np.argmin(np.abs(nf4_values - x))
数学原理:
最近邻搜索:对输入值xxx,找到预定义值中最接近的:
index=arg mink∣x−vk∣\text{index} = \argmin_{k} |x - v_k|index=kargmin∣x−vk∣
其中,nf4_values=vkv_kvk
数学性质:
•在[-1,1]区间内误差最小化
•对接近0的值更密集(匹配权重的高概率密度区)
1.3.2. NF8(8-bit归一化浮点)实现原理
核心思想
动态范围自适应 + 高精度分桶,用8-bit(256个值)处理激活值等高动态范围数据。
关键步骤
1.3.2.1 动态值生成
基于数据分布生成量化值
samples = np.random.normal(0, 1, 1_000_000) # 模拟数据分布
values = np.quantile(samples, np.linspace(0, 1, 256))
1.3.2.2数学原理:
vk=inf{x:P(X≤x)≥k255},k=0,...,255v_k = \inf \left\{ x : P(X \leq x) \geq \frac{k}{255} \right\}, \quad k=0,...,255vk=inf{x:P(X≤x)≥255k},k=0,...,255
即这就是 分位数定义:
vi=F−1(i255),i=0,1,...,255v_i = F^{-1}\left(\frac{i}{255}\right), \quad i=0,1,...,255vi=F−1(255i),i=0,1,...,255
其中,F−1F^{-1}F−1是标准正态分布的反函数(即 CDF 的反函数)
def encode_tensor(x):
expanded_x = np.expand_dims(x, -1) # [..., 1]
expanded_v = values.reshape([1]*x.ndim+[256]) # [1,1,...,256]
return np.argmin(np.abs(expanded_x - expanded_v), axis=-1)
实现
import numpy as np
class NF4Quantizer:
def __init__(self):
# 预定义的NF4量化值(来自QLoRA论文)
self.nf4_values = np.array([
-1.0, -0.6961928009986877, -0.5250730514526367, -0.39491748809814453,
-0.28444138169288635, -0.18477343022823334, -0.09105003625154495, 0.0,
0.07958029955625534, 0.16093020141124725, 0.24611230194568634, 0.33791524171829224,
0.44070982933044434, 0.5626170039176941, 0.7229568362236023, 1.0
], dtype=np.float32)
def encode(self, x):
"""将张量编码为NF4索引(自动处理任意形状)"""
# 扩展维度以便广播计算 [原始形状, 1] vs [16]
expanded_x = np.expand_dims(x, -1)
expanded_values = self.nf4_values.reshape([1]*x.ndim + [16])
# 计算所有元素的最近邻索引
return np.argmin(np.abs(expanded_x - expanded_values), axis=-1)
def decode(self, indices):
"""将NF4索引解码为原始张量形状"""
return np.take(self.nf4_values, indices)
# 使用示例
if __name__ == "__main__":
nf4 = NF4Quantizer()
# 向量测试
vec = np.array([0.8, -1.2, 0.3, -0.5, 1.7], dtype=np.float32)
quant_vec = nf4.encode(vec)
dequant_vec = nf4.decode(quant_vec)
print("向量量化结果:")
print(f"原始: {vec}")
print(f"量化索引: {quant_vec}")
print(f"反量化: {dequant_vec}")
print(f"误差: {np.abs(vec - dequant_vec).max():.4f}")
# 矩阵测试
mat = np.random.randn(3, 2).astype(np.float32)
quant_mat = nf4.encode(mat)
print("\n矩阵量化结果:")
print(f"原始矩阵:\n{mat}")
print(f"量化索引:\n{quant_mat}")
向量量化结果:
原始: [ 0.8 -1.2 0.3 -0.5 1.7]
量化索引: [14 0 11 2 15]
反量化: [ 0.72295684 -1. 0.33791524 -0.52507305 1. ]
误差: 0.7000
矩阵量化结果:
原始矩阵:
[[ 0.95008844 -0.1513572 ]
[-0.10321885 0.41059852]
[ 0.14404356 1.4542735 ]]
量化索引:
[[15 5]
[ 6 12]
[ 9 15]]
class NF8Quantizer:
def __init__(self, num_bins=256, data_range=(-2, 2)):
"""
参数:
num_bins: 量化级别数 (默认256)
data_range: 预期数据范围 (根据实际数据分布调整)
"""
# 基于数据范围生成非均匀量化值
self.num_bins = num_bins
self.data_range = data_range
self._generate_quant_values()
def _generate_quant_values(self):
"""生成服从正态分布的分位数"""
samples = np.random.normal(0, 1, 1000000)
samples = samples[(samples >= self.data_range[0]) & (samples <= self.data_range[1])]
self.nf8_values = np.quantile(
samples,
np.linspace(0, 1, self.num_bins)
).astype(np.float32)
def encode(self, x):
"""将张量编码为NF8索引"""
expanded_x = np.expand_dims(x, -1)
expanded_values = self.nf8_values.reshape([1]*x.ndim + [self.num_bins])
return np.argmin(np.abs(expanded_x - expanded_values), axis=-1)
def decode(self, indices):
"""将NF8索引解码为原始张量形状"""
return np.take(self.nf8_values, indices)
# 使用示例
if __name__ == "__main__":
nf8 = NF8Quantizer()
# 三维张量测试
tensor_3d = np.random.randn(2, 2, 3).astype(np.float32)
quant_3d = nf8.encode(tensor_3d)
dequant_3d = nf8.decode(quant_3d)
print("\n三维张量量化结果:")
print(f"原始张量形状: {tensor_3d.shape}")
print(f"量化索引形状: {quant_3d.shape}")
print(f"最大误差: {np.abs(tensor_3d - dequant_3d).max():.6f}")
2、FP4
原理:
FP4(4-bit Floating Point)量化是一种将高精度浮点数(如FP32)压缩为4-bit低精度格式的技术,通过牺牲一定精度来大幅减少存储和计算开销。其核心原理是模仿标准浮点数的存储结构,但极度精简位数。以下是详细解析:
2.4.1. FP4的二进制结构
FP4通常采用类似IEEE浮点数的设计,但仅有4位,分配方式有多种,最常见的两种格式:
(1) 1-2-1格式(符号位-指数位-尾数位)
位域 符号位 (S) 指数位 (E) 尾数位 (M)
比特数 1-bit 2-bit 1-bit
示例 0 10 1
• 符号位 (S):0表示正数,1表示负数。
• 指数位 (E):2-bit可表示0-3(实际指数需减去偏置,例如E_true = E - 1)。
• 尾数位 (M):1-bit表示0或1(隐含的1.前缀,即实际尾数为1.0或1.5)。
(2) 1-1-2格式(符号位-指数位-尾数位)
位域 符号位 (S) 指数位 (E) 尾数位 (M)
比特数 1-bit 1-bit 2-bit
示例 1 0 10
• 尾数精度更高(可表示1.0, 1.25, 1.5, 1.75),但动态范围更小(因指数位减少)。
2.4.2. FP4量化步骤(以1-2-1格式为例)
步骤1:确定量化参数
• 输入范围:假设输入张量 X = [0.8, -1.2, 0.4, -0.6, 1.5]。
• 指数偏置 (Bias):设为1(使得E_true = E - 1,支持负指数)。
步骤2:对每个数值进行编码
以 x = 0.8 为例:
- 符号位:0(正数)。
- 计算指数:
• 找到最小的 E 使得 1.0 * 2^(E-1) ≤ 0.8:
◦ E=1 → 1.0 * 2^0 = 1.0 > 0.8(不满足)
◦ E=0 → 1.0 * 2^-1 = 0.5 ≤ 0.8(满足)
• 因此 E = 0(实际指数 E_true = -1)。 - 计算尾数:
• 尾数 M 的选择应使 (1 + M/2) * 2^E_true 最接近 0.8:
◦ M=0 → 1.0 * 0.5 = 0.5(误差 0.3)
◦ M=1 → 1.5 * 0.5 = 0.75(误差 0.05,更优)
• 选择 M = 1。 - FP4编码:S=0, E=0, M=1 → 二进制 0b0001(十进制 1)。
步骤3:反量化
• 解码 0b0001:
• S=0, E=0, M=1 → (1 + 1/2) * 2^(0-1) = 1.5 * 0.5 = 0.75。
• 与原始值 0.8 的误差为 0.05。 - FP4的动态范围与精度
动态范围
• 1-2-1格式:
• 最小正数:(1.0) * 2^{-1} = 0.5
• 最大正数:(1.5) * 2^{2} = 6.0
• 范围:[-6.0, -0.5] ∪ [0.5, 6.0]。
可表示的值
| 二进制 | 符号 (S) | 指数 (E) | 尾数 (M) | 计算值 |
|--------|----------|----------|----------|----------------------------|
| 0 00 0 | + | -1 | 1.0 | 1.0 × 2⁻¹ = 0.5 |
| 0 00 1 | + | -1 | 1.5 | 1.5 × 2⁻¹ = 0.75 |
| 0 01 0 | + | 0 | 1.0 | 1.0 × 2⁰ = 1.0 |
| 0 01 1 | + | 0 | 1.5 | 1.5 × 2⁰ = 1.5 |
| 0 10 0 | + | +1 | 1.0 | 1.0 × 2¹ = 2.0 |
| 0 10 1 | + | +1 | 1.5 | 1.5 × 2¹ = 3.0 |
| 0 11 0 | + | +2 | 1.0 | 1.0 × 2² = 4.0 |
| 0 11 1 | + | +2 | 1.5 | 1.5 × 2² = 6.0 |
表格说明:
- 二进制:3位格式(符号1位 + 指数2位 + 尾数1位)。
- 符号 (S):
+表示正数(二进制0),-表示负数(二进制1)。 - 指数 (E):2位移码(偏移量1),
00→-1,01→0,10→+1,11→+2。 - 尾数 (M):隐含前导1,尾数位
0=1.0,1=1.5(即1 + 0.5)。 - 计算值:基于公式 ( \text{值} = M \times 2^{E} )。
实现
import numpy as np
class FP4Quantizer:
def __init__(self, exponent_bias=1):
"""
FP4量化器 (1-2-1格式: 符号位-2位指数-1位尾数)
参数:
exponent_bias: 指数偏置 (E_true = E - bias)
"""
self.bias = exponent_bias
self.max_exp = (1 << 2) - 1 # 2位指数最大值为3
self.min_denorm = 0.5 # 最小正规化数 (1.0 * 2^{-bias})
def encode(self, x):
"""
将FP32数值编码为FP4 (返回整数0-15表示4位二进制)
"""
if x == 0:
return 0
# 符号位
sign = 0 if x > 0 else 1
x_abs = np.abs(x)
# 处理过小数值 (小于最小正规化数)
if x_abs < self.min_denorm:
return sign << 3 # 指数=0,尾数=0 (表示为0)
# 计算最优指数和尾数
best_err = float('inf')
best_e, best_m = 0, 0
for e in range(self.max_exp + 1):
e_true = e - self.bias
scale = 2.0 ** e_true
for m in [0, 1]:
# 尾数解释: m=0→1.0, m=1→1.5
mantissa = 1.0 + 0.5 * m
quantized = mantissa * scale
err = abs(quantized - x_abs)
if err < best_err:
best_err = err
best_e, best_m = e, m
# 组合为4位: [sign(1)|exp(2)|mantissa(1)]
return (sign << 3) | ((best_e & 0b11) << 1) | (best_m & 0b1)
def decode(self, fp4):
"""
将FP4整数解码为FP32数值
"""
if fp4 == 0:
return 0.0
# 解析位域
sign = (fp4 >> 3) & 0b1
e = (fp4 >> 1) & 0b11
m = fp4 & 0b1
# 计算实际值
e_true = e - self.bias
mantissa = 1.0 + 0.5 * m
value = mantissa * (2.0 ** e_true)
return -value if sign else value
def get_quantized_values(self):
"""返回所有可表示的FP4值及其二进制表示"""
values = []
for i in range(16):
binary = f"{i:04b}"
s, e, m = binary[0], binary[1:3], binary[3]
dec = self.decode(i)
values.append((i, binary, f"s={s}, e={e}, m={m}", dec))
return values
# 使用示例
if __name__ == "__main__":
quantizer = FP4Quantizer(exponent_bias=1)
# 单值量化测试
x = 0.8
fp4 = quantizer.encode(x)
x_dequant = quantizer.decode(fp4)
print(f"原始值: {x:.4f} → FP4编码: {fp4:04b} → 反量化: {x_dequant:.4f} (误差: {abs(x - x_dequant):.4f})")
# 打印所有可表示值
print("\nFP4 (1-2-1格式) 可表示的值:")
for idx, bin_, fields, val in quantizer.get_quantized_values():
print(f"{idx:2d} {bin_} {fields:12} → {val:+.4f}")
import numpy as np
class FP8Quantizer:
def __init__(self, exponent_bias=7):
"""
FP8量化器 (1-4-3格式: 符号位-4位指数-3位尾数)
参数:
exponent_bias: 指数偏置 (E_true = E - bias)
"""
self.bias = exponent_bias
self.max_exp = (1 << 4) - 1 # 4位指数最大值为15
self.min_denorm = 2.0 ** (1 - self.bias) # 最小正规化数
def encode(self, x):
"""
将FP32数值编码为FP8 (返回整数0-255表示8位二进制)
"""
if x == 0:
return 0
# 符号位
sign = 0 if x > 0 else 1
x_abs = np.abs(x)
# 处理过小数值 (小于最小正规化数)
if x_abs < self.min_denorm:
return sign << 7 # 指数=0,尾数=0 (表示为0)
# 处理特殊值 (超过最大可表示范围)
max_representable = (1.875) * (2.0 ** (self.max_exp - self.bias))
if x_abs > max_representable:
return (sign << 7) | 0b01111111 # 无穷大
# 计算最优指数和尾数
best_err = float('inf')
best_e, best_m = 0, 0
for e in range(1, self.max_exp): # 跳过全0和全1的指数
e_true = e - self.bias
scale = 2.0 ** e_true
# 尾数解释: 3位尾数 → [1.0, 1.125, 1.25, ..., 1.875]
for m in range(8):
mantissa = 1.0 + m * 0.125
quantized = mantissa * scale
err = abs(quantized - x_abs)
if err < best_err:
best_err = err
best_e, best_m = e, m
# 组合为8位: [sign(1)|exp(4)|mantissa(3)]
return (sign << 7) | ((best_e & 0b1111) << 3) | (best_m & 0b111)
def decode(self, fp8):
"""
将FP8整数解码为FP32数值
"""
if fp8 == 0:
return 0.0
# 解析位域
sign = (fp8 >> 7) & 0b1
e = (fp8 >> 3) & 0b1111
m = fp8 & 0b111
# 处理无穷大
if e == 0b1111:
return float('-inf') if sign else float('inf')
# 计算实际值
e_true = e - self.bias
mantissa = 1.0 + m * 0.125
value = mantissa * (2.0 ** e_true)
return -value if sign else value
def get_quantized_values(self):
"""返回所有可表示的FP8值及其二进制表示(抽样显示)"""
samples = []
for i in range(0, 256, 16): # 每16个抽样一个
binary = f"{i:08b}"
s, e, m = binary[0], binary[1:5], binary[5:]
dec = self.decode(i)
samples.append((i, binary, f"s={s}, e={e}, m={m}", dec))
return samples
# 使用示例
if __name__ == "__main__":
quantizer = FP8Quantizer(exponent_bias=7)
# 单值量化测试
x = 3.1415926
fp8 = quantizer.encode(x)
x_dequant = quantizer.decode(fp8)
print(f"原始值: {x:.7f} → FP8编码: {fp8:08b} → 反量化: {x_dequant:.7f} (误差: {abs(x - x_dequant):.7f})")
# 动态范围测试
print(f"\n动态范围:")
print(f"- 最小正规化正数: {quantizer.decode(0b00001000):.4f}")
print(f"- 最大正规化正数: {quantizer.decode(0b01111011):.4f}")
# 打印抽样值
print("\nFP8 (1-4-3格式) 抽样值:")
for idx, bin_, fields, val in quantizer.get_quantized_values():
print(f"{idx:3d} {bin_} {fields:15} → {val:+.6f}")
1.位分配:
•1位符号位 + 4位指数 + 3位尾数 = 8位
•尾数精度更高(8种取值:1.0, 1.125, …, 1.875)
2.特殊值处理:
•指数全0:表示0或非正规化数(本实现简化处理为0)
•指数全1:表示无穷大(±inf)
3.动态范围(当exponent_bias=7时):
•最小正规化正数:1.0 × 2^{-6} ≈ 0.015625
•最大正规化正数:1.875 × 2^7 ≈ 240.0
4.误差优化:
•通过遍历所有可能的指数/尾数组合选择最优逼近
•相比FP4,FP8的量化误差显著降低(示例中π的量化误差约0.003)
2.3、NF4 vs FP4 直观对比
| 特性 | NF4(NormalFloat) | FP4(Float) |
|---|---|---|
| 量化方式 | 非均匀(基于正态分布优化) | 均匀(线性分割) |
| 数值分布 | 假设,权重近似正态分布 | 无假设,均匀覆盖所有值 |
| 计算复杂度 | 较高(需统计分布) | 较低(直接均匀分割) |
| 适用场景 | 大多数 LLM(如 LLaMA、Phi-3) | 数值分布均匀的任务 |
3、选择
1、 优先用 NF4:
• 在 BitsAndBytesConfig 中设置 bnb_4bit_quant_type=“nf4”(默认)。
• 适合绝大多数 LLM,显存节省和精度损失平衡较好。
-
特殊情况用 FP4:
• 如果模型权重分布均匀(罕见),可以尝试 bnb_4bit_quant_type=“fp4”。• 通常效果不如 NF4,除非针对特定任务优化。
总结
• NF4 是非均匀量化,针对神经网络权重(正态分布)优化,推荐默认使用。
• FP4 是均匀量化,简单但效率较低,适合特殊场景。
• 在 load_in_4bit=True 时,Hugging Face 的 transformers 库默认使用 nf4,无需手动更改。
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








