[leetcode]119. 杨辉三角 II

最新推荐文章于 2025-11-21 14:33:46 发布

原创最新推荐文章于 2025-11-21 14:33:46 发布 · 455 阅读

4 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode #算法 #职场和发展

文章讲述了如何使用动态规划方法解决给定非负索引rowIndex获取杨辉三角指定行的问题，通过一维数组缓存上一行数据，从后向前计算，实现时间复杂度为O(n)。

前言：剑指offer刷题系列

问题：

给定一个非负索引 rowIndex，返回「杨辉三角」的第 rowIndex 行。

在「杨辉三角」中，每个数是它左上方和右上方的数的和。

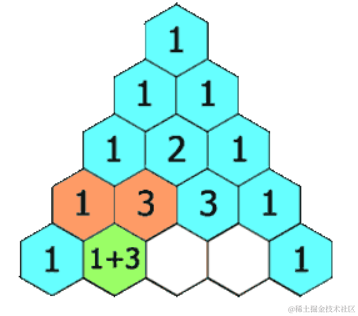
示例：

输入: rowIndex = 3
输出: [1,3,3,1]

思路：

杨辉三角是一个数字三角形，每个数字等于它上方两个数字之和，第一行是1，第二行是1 1，以此类推。之前做过一个生成杨辉三角题，这次是返回杨辉三角的第rowIndex行。这是一个动态规划问题。

每次只用到上一行，所以只有一个一维数组来缓存就行，每行都是从后向前计算，以免覆盖，时间复杂度就从O(n^2)降到O(n)。

由示例，可以注意到输入的是rowIndex，这一行的长度是rowIndex+1.

下面是对代码的解释：

首先创建一个长度为 rowIndex + 1 的列表 res，并将其所有元素初始化为1。这是杨辉三角的起始行，每一行的两端都是1。
然后，从第三行开始，迭代生成每一行的数据。外层循环 for r 用于遍历行数，从第三行（行数为2）到指定的 rowIndex 行。
内层循环 for c 用于遍历当前行的元素，从倒数第二个元素开始，直到第一个元素。这是因为每行的第一个元素总是1，不需要计算。
在内层循环中，计算当前行的每个元素的值。每个元素等于上一行对应位置的元素和上一行前一个位置的元素之和。
返回生成的第 rowIndex 行的列表。

时间复杂度O(n^2)

空间复杂度O(n)

基于上述思考，代码如下：

class Solution:
    def getRow(self, rowIndex: int) -> List[int]:
        res = [1] * (rowIndex + 1)
        for r in range(2, rowIndex + 1):
            for c in range(r - 1, 0, -1):
                res[c] = res[c] + res[c - 1]
        return res

执行结果如下图：

时间和存储消耗都是很不错的。

学到的知识点：

动态规划思想： 代码中使用了动态规划的思想来生成杨辉三角的指定行。动态规划通常用于解决具有递归结构的问题，通过保存并重复使用中间结果来提高效率。