DeepGo: Predictive Directed Greybox Fuzzing 翻译

DeepGo: 可预测的定向灰盒模糊测试

    摘要——定向灰盒模糊测试（DGF）是一种旨在通过预定义的目标位置强化对脆弱代码区域测试的有效方法。最先进的DGF技术通过重新定义和优化适应度指标，精准且快速地到达目标位置。然而，适应度指标的优化主要基于启发式算法，这些算法通常依赖于历史执行信息，缺乏对尚未执行路径的预见性。因此，那些具有复杂约束的难以执行的路径会阻碍DGF到达目标，使DGF的效率降低。

    在本文中，我们提出了 DeepGo，一种能够结合历史和预测信息的预测性定向灰盒模糊测试工具，通过最优路径引导DGF到达目标位置。我们首先提出了路径转换模型，将DGF建模为通过特定路径转换序列到达目标位置的过程。通过变异生成的新种子会引发路径转换，与高回报路径转换序列对应的路径表明通过该路径有很大可能到达目标位置。然后，为了预测路径转换及其对应的回报，我们使用深度神经网络构建了虚拟集成环境（VEE），该环境逐步模拟路径转换模型，并预测尚未采取的路径转换回报。为了确定最优路径，我们开发了用于模糊测试的强化学习（RLF）模型，用于生成具有最高序列回报的路径转换序列。RLF模型可以结合历史和预测的路径转换，生成最优的路径转换序列，同时制定策略以引导模糊测试的变异策略。最后，为了执行高回报路径转换序列，我们提出了“动作组”（action group）的概念，全面优化模糊测试的关键步骤，以高效实现到达目标的最优路径。我们在包含25个程序、总计100个目标位置的2个基准测试集上对DeepGo进行了评估。实验结果表明，与AFLGo、BEACON、WindRanger和ParmeSan相比，DeepGo在到达目标位置上的速度分别提升了3.23倍、1.72倍、1.81倍和4.83倍，在暴露已知漏洞方面的速度分别提升了2.61倍、3.32倍、2.43倍和2.53倍。

1引言

    定向灰盒模糊测试（DGF） 是一种高效的技术，专为测试脆弱的代码区域而设计。通过定义一个可衡量的适应度指标，定向灰盒模糊测试工具能够选择有潜力的种子，并给予它们更多的变异机会，使其逐步接近目标位置。例如，基于被测程序（PUT）的调用图和控制流图信息，主流的DGF技术使用输入与目标位置之间的距离作为适应度指标，以辅助种子选择和能量分配。离目标位置更近的种子被视为有前途的，优先处理。DGF大部分时间都花在到达这些目标位置上，避免浪费资源在无关的部分上，因此，它特别适用于包括补丁测试、错误重现和潜在问题代码验证等测试场景。

    为了增强定向性并提高效率，最先进的DGF方法利用启发式方法重新定义和优化适应度指标。例如，一些DGF技术基于执行路径相似性（如Hawkeye）、数据条件（如CAFL）和数据流信息（如WindRanger）来重新定义适应度指标。一些定向模糊测试工具采用基于序列的方法来增强定向性，例如扩展给定的目标序列（如Berry）和使用“释放后使用”序列作为指导（如Lolly）。还有一些DGF技术通过修剪到目标的不可达路径（如BEACON）以及构建可查询的oracle来引导模糊测试（如MC2），从而提高效率。然而，在模糊测试过程中，种子的变异使得执行路径具有不确定性。这些启发式方法通常依赖于历史执行信息，缺乏对尚未执行路径的预见性。例如，当使用基本块级别距离作为适应度指标时，距离较短的种子会被优先考虑，而不考虑路径的可行性。结果，那些具有复杂约束的难以执行的路径会阻碍DGF到达目标位置，降低其效率。因此，本论文旨在设计一个能够预测关键执行信息和最优路径的预测性定向灰盒模糊测试工具。通过结合历史执行信息和预测的未来执行信息，模糊测试工具能够智能地生成通向目标位置的最优且可行的路径。通过避免不可行和难以执行的路径，模糊测试工具可以更精确且高效地到达目标位置。

    为此，我们提出将DGF建模为通过特定路径转换序列到达目标位置的过程，并将该模型命名为路径转换模型。通过变异生成的新种子会引发路径转换，我们使用奖励来评估路径转换对模糊测试工具的即时影响。我们使用序列奖励来评估通过一系列路径转换到达目标位置的难度。可以生成对应于最高序列奖励的路径，这将引导模糊测试工具更高效地到达目标位置。为了实现这一目标，我们需要解决三个挑战。高奖励路径转换序列表明通过它到达目标位置的可能性很高。与之前的启发式方法相比，该模型考虑了通过不同路径转换序列到达目标位置的难度。此外，通过分析不同路径转换序列的序列奖励，可以确定一条最优路径。

    挑战 1：如何预测尚未发生的路径转换？为了生成通往目标位置的最优路径，我们需要收集所有潜在的路径转换信息。然而，现有技术只能收集已知的路径转换信息，不适用于预测未来的路径转换。在DGF中，不同的变异会引发不同的路径转换。在有限的时间预算内，模糊测试工具无法对所有种子尝试所有变异（例如，使用所有变异器对所有种子字节进行变异）。此外，随机选择变异器和字节进行变异可能会导致选择低效的变异器，或者错过关键字节。因此，我们应当预测尚未发生的变异所引发的潜在路径转换及其对应的奖励。

    挑战 2：如何在大量路径转换中确定最优路径？在路径转换模型中，较高的序列奖励意味着通过该路径转换序列到达目标位置的可能性更高。最优路径可以通过具有最高序列奖励的路径转换序列表示。然而，历史路径转换与预测路径转换的组合会产生大量不同序列奖励的路径转换序列。因此，我们需要有效地评估所有路径转换序列的序列奖励，并设计策略来指导变异，从而实现最优路径。

    挑战 3：如何通过优化模糊测试策略来执行最优路径转换序列？由于DGF仍采用随机变异策略，模糊测试工具所覆盖的路径是随机且不断变化的。然而，基于路径转换模型，为了有效地通过最优路径转换序列引导模糊测试工具朝向目标位置，我们应该全面优化模糊测试的关键步骤，例如种子选择、能量分配、变异器调度、循环次数（如Havoc中的循环）和变异位置选择。因此，我们需要能够同时优化模糊测试的关键步骤，以高效执行最优路径转换序列。

    为了应对这些挑战，我们提出了 DeepGo，一种预测性的定向灰盒模糊测试工具。基于路径转换模型，我们将DGF中的路径覆盖、对种子的变异、路径转换及路径转换引起的种子值变化提取为四元组（路径、动作、下一路径、奖励）（见第三节）。针对挑战1，我们使用深度神经网络（DNN）构建一个虚拟集合环境（VEE）。给定一个路径和一个动作，经过充分训练的VEE能够预测潜在的路径转换及其对应的奖励。随着提供给VEE的路径转换信息的增加，VEE可以逐渐模仿路径转换模型，并预测尚未执行的变异引起的路径转换，这大大提高了DGF的效率。针对挑战2，我们提出了一个模糊测试强化学习（RLF）模型来确定最优路径。为了给RLF提供前瞻性，我们使用k步分支回滚策略不断从VEE获取预测的路径转换。通过结合历史路径转换和预测路径转换，RLF模型被训练以评估由不同变异引起的路径转换序列的期望序列奖励，并确定最高的序列奖励。此外，模型可以学习最优路径的策略，以指导模糊测试的变异策略。针对挑战3，为了执行最优路径，我们基于动作组的概念优化模糊测试策略。在动作组中，我们全面考虑五个关键步骤，包括种子选择、能量分配、Havoc中的循环选择、变异器调度和变异位置选择。在RLF模型生成的变异策略下，我们使用**多元粒子群优化（MPSO）**算法同时优化这些步骤，以实现期望的变异，生成路径转换序列，最终通过最优路径到达目标位置。

    总的来说，我们主要做出了以下贡献：

1. 我们提出了路径转换模型，该模型将定向灰盒模糊测试（DGF）建模为通过特定路径转换序列到达目标位置的过程。基于路径转换模型，我们使用序列奖励作为适应度指标，以评估通过一系列路径转换到达目标位置的难度。

1. 我们构建了虚拟集合环境（VEE），使用深度神经网络（DNN）来模拟路径转换模型，并预测潜在的路径转换及其对应的奖励，而无需实际执行路径，这大大提高了效率。

1. 我们提出了强化学习模糊测试（RLF）模型，该模型可以结合历史信息和预测信息，以生成通往目标位置的最优路径。通过避免不可行和难以执行的路径，具有最高序列奖励的最优路径可以高效而准确地引导模糊测试工具到达目标位置。
2. 我们在动作组的粒度上优化了模糊测试的变异策略，这比单一策略优化更高效。在动作组中，我们考虑了模糊测试的五个关键步骤，并使用**多元粒子群优化（MPSO）**算法同时对它们进行优化。

1. 我们实现并评估了DeepGo。评估结果表明，**虚拟集合环境（VEE）**能够以高精度预测路径转换，而DeepGo能够比基线模糊测试工具更快地到达目标位置。

2 背景

    定向灰盒模糊测试。沿袭AFLGo的思路，现有的DGF技术基于调用图和控制流图计算输入与预定义目标之间的距离，并将该距离与其他指标（如条件复杂度）结合，以形成适应度指标。然后，在运行时，定向灰盒模糊测试技术根据适应度指标设计不同的能量调度，为更优先的种子分配更多能量。它将可达性视为一个优化问题，以最小化生成的输入与目标之间的距离。

    深度神经网络。近年来，深度神经网络（DNN）展示了其近似复杂非线性和非凸函数的能力，并在模式识别中模仿环境的能力。DNN已经在一些模糊测试工作中得到了应用，例如NEUZZ、MTFuzz和FUZZGUARD，以模拟程序分支行为。总的来说，这些工作在模糊测试过程中收集生成的变异输入作为DNN的输入，并记录覆盖的程序分支作为标签来训练DNN。通过这种方式，DNN能够模拟程序的分支行为，并引导模糊测试优化。这些工作的评估证明了DNN适合模拟模糊测试环境。

    强化学习。强化学习（即RL）通常用于解决序列决策问题（例如马尔可夫过程）。在RL模型中，智能体会不断采取行动与环境进行互动，并接收反馈，即奖励。基于来自环境的反馈（表示为四元组（状态、动作、下一个状态、奖励）），RL模型将优化行动选择策略（即RL中的策略），以获得最大奖励。沿袭AFLGo的思路，我们可以将DGF建模为马尔可夫过程，并应用RL模型来优化模糊测试策略，例如变异操作符的选择和变异字节的选择。

    基于模型的策略优化。基于模型的策略优化（MBPO）是一种基于模型的强化学习方法，由两个模块组成：虚拟环境和强化学习网络。首先，MBPO使用深度神经网络（DNN）创建一个虚拟环境，以替代真实环境。其次，MBPO允许智能体与虚拟环境进行互动，以获得大量的路径转移。然后，MBPO可以不断训练强化学习网络，并基于路径转移学习出最大化智能体奖励的策略。在本文中，我们借鉴了MBPO的一些方法，例如k步分支回滚策略，以结合DNN和RL。

    粒子群优化。粒子群优化（PSO）算法是一种进化计算技术，起源于对鸟群觅食行为的研究。它已被应用于提高模糊测试的效率，例如，MOPT使用PSO算法基于模糊测试历史信息优化变异操作符的选择概率。PSO的主要思想是通过个体之间的合作与信息共享来寻找最佳解决方案。PSO算法使用无质量粒子模拟鸟群中的鸟，这些粒子具有两个主要属性：速度和位置。速度表示运动的快慢，位置表示运动的方向。每个粒子在搜索空间中独立搜索最优解，并将其记录为局部最佳值。然后，局部最佳值在整个群体中共享，以找到全局最佳值作为最优解。群体中的所有粒子会根据共享的局部最佳值和全局最佳值调整它们的速度和位置。

3 路径转移模型

    在本文中，我们提出了路径转移模型，该模型将定向模糊测试（DGF）建模为通过特定路径转移序列达到目标站点的过程。由变异生成的新种子将导致路径转移，我们使用奖励来评估路径转移对模糊测试器的即时影响。具有最高序列奖励的路径转移序列决定了到达目标的最佳路径。在本节中，我们将DGF中的关键元素映射到路径转移模型，并量化路径转移和动作的有效性。

A. 路径转移模型中的元素

路径。每条路径对应模糊测试器种子队列中的一个种子。我们使用AFL中的trace_bits来记录路径中覆盖的分支及其命中次数，从而区分不同的路径。

动作。模糊测试器的动作指的是在特定位置对种子进行变异。我们关注变异发生的位置（即字节），而不是使用的变异器。模糊测试器通过一系列动作逐步达到目标站点。

路径转移。如果新输入的执行路径与种子的执行路径不同，对种子的变异会导致路径转移。如果新输入的路径与种子的路径相同，则该变异会导致自路径转移。

奖励。路径转移的奖励表示路径转移所导致的种子值的变化。

策略。策略是模糊测试器在每条路径中选择动作的策略，表示为与动作对应的概率列表。在该策略下，模糊测试器会以不同的概率选择动作。

    我们使用图1来说明路径转移模型。图1显示了一个示例程序的执行树，其中节点代表基本块，边代表基本块之间的转移。用绿色标记的执行路径 path1 由种子 s1 覆盖，用蓝色标记的执行路径 path2 由种子 s2 覆盖，而用黄色标记的执行路径 path3 由种子 s3 覆盖。标记为橙色的节点是目标基本块，路径 path3 是可以到达目标站点的最优路径。在模糊测试过程中，首先，模糊测试器采取行动，将种子 s1 变异生成新种子 s2，使得 path1 转移到 path2。然后，模糊测试器再对种子 s2 进行变异，使得 path2 转移到 path3，并到达目标站点。通过这两个路径转移，模糊测试器生成了由路径转移序列（路径转移1，路径转移2）表示的最优路径 path3，成功到达目标。

图1 路径转移模型示例图

B. 量化路径转移和动作

    模糊器采取不同的操作来变异种子将导致不同的路径转移，我们使用奖励来量化路径转移的有效性，并使用期望序列奖励来量化动作的有效性。

    种子值。我们使用种子值来评估不同路径对模糊器达到目标站点的贡献。种子值是根据与路径相对应的种子的四个特征计算得出的：（1）种子与目标的距离，（2）满足分支反转的难度，（3）执行速度，以及（4）种子是否被标记为“优先”。在定向模糊测试中，较短的种子距离意味着模糊器可以通过满足更少的路径约束来达到目标站点，而较低的难度则意味着模糊器更容易满足通往目标站点的路径约束。此外，在种子执行过程中，模糊器可能会陷入循环（例如，while 循环和 for 循环），这会降低执行速度，并且对模糊器达到目标站点没有贡献。因此，为了提高模糊测试效率，我们更倾向于执行速度更快的种子。此外，我们更喜欢被标记为“优先”的种子，因为这些种子可以覆盖所有已探索的分支。通过对优先种子进行模糊测试，我们可以对所有已探索的分支进行反转，以覆盖通往目标站点的新分支。根据 AFL 和 AFLGo 的方法，（1）、（3）和（4）的元素可以通过在模糊测试过程中简单地记录执行信息来获得。在这里，我们主要解释“难度”概念及其计算。

    我们使用分支概率来衡量满足分支反转的难度，该概率基于分支命中的统计信息。我们首先在静态分析中获取每个分支的兄弟分支信息。如果已覆盖分支的兄弟分支仍未被覆盖（即未探索的分支），则满足分支反转以覆盖未探索的分支将允许模糊器从已覆盖路径转移到新路径。接着，我们统计分支命中次数以计算未探索分支的分支概率。如果模糊器在使用变异输入时始终命中已覆盖的分支，但无法命中未探索的分支，这表明模糊器在满足分支反转方面存在困难。最后，我们通过分支概率量化满足分支反转的难度：

其中，ubr 表示未探索的分支。我们检查已覆盖分支的兄弟分支是否被覆盖，以找到未探索的分支。ϕ(cond) 表示在相同条件下的所有分支的集合。hitbr 表示在模糊过程中记录的分支命中次数。P(ubr) 表示未探索分支的分支概率，由于我们认为未探索的分支始终有被模糊覆盖的概率，因此该概率不会为0。我们使用一个种子路径中所有未探索分支的分支概率的算术平均值来估计满足分支反转的难度：

其中，s 表示种子，EDs 表示估计的难度，Φ(s) 表示包含种子路径中所有未探索分支的集合。

    因此，距离、难度、执行速度和“优先”都可以被定量测量和计算，从而计算种子值。我们使用熵权法 [26] 根据四个因素的信息熵来确定它们的权重。信息熵值较小的因素会使其权重较小，表示该因素对种子值的整体评估影响较小。

其中，Vs(pt) 表示路径 pt 的种子值，W1、W2、W3 和 W4 是基于熵权法计算的权重。ds 表示种子距离，Exs 表示执行速度，Fvs 指示是否为优先种子，该值可以是 0 或 1。熵权法 [26] 是一种常用的多元素综合评价方法。计算不同元素权重的步骤如下：

（1）计算每个元素的熵：

（2）计算每个元素的权重：

（3）标准化每个元素的权重：

其中 𝑊𝑗′表示第 𝑗个元素的归一化权重。熵权法的核心思想是通过计算每个元素的熵来确定它们的权重，从而进行多元素综合评估。

    然后，我们根据种子值计算奖励，以评估路径转换的有效性：

其中rpt,at,pt+1代表奖励值，at代表模糊器从路径pt转移到pt+1所采取的的动作，Vspt,Vspt+1代表路径pt和pt+1的种子值。我们使用四元组pt,at,pt+1,rt来表示一个路径转移。​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​

    预期序列奖励。在路径转换模型中，根据策略选择的动作引发的路径转换会影响后续的路径转换序列，从而影响到目标位置的到达。为了评估路径转换对达到目标位置的贡献，我们定义了预期序列奖励，即模糊器按照某一策略生成的路径转换序列奖励的预期和。它可以通过贝尔曼方程递归计算【4】：

其中，p′ ∼ P 表示从路径 p 转移到路径 p′ 的概率。γ 表示折扣因子，随后路径转换对预期序列奖励的影响将逐渐减弱。r(p, a, p′) 表示路径转换的奖励。Vπt(p')

表示路径p′的转换值，计算方法如下：

其中，pter 表示终止路径。如果路径的所有操作都只能引发自路径转换，我们将其视为终止路径。π 代表选择动作的策略（例如，在 AFL 中，模糊测试器使用随机策略选择变异操作）。π(a|p) 表示在策略 π 下路径 p 选择动作 a 的概率。如果 p′ 是终止状态，则其转换值为 0。如果不是，则其转换值等于所有操作的预期序列奖励的加权平均值。贝尔曼方程用于递归更新转换值和预期序列奖励，直到路径成为终止路径。通过最大化预期序列奖励，模糊测试器可以学习一种策略，以最大化长期累计奖励。

4 方法

A. DeepGo概述

    基于路径转换模型，我们设计了一种可预测的定向灰盒模糊测试器——DeepGo。DeepGo 使用深度神经网络（DNNs）来预测潜在的路径转换及其相应的奖励。然后，它通过强化学习结合历史和预测的路径转换，获取最佳的路径转换序列及其对应的策略。最后，基于动作组，DeepGo 全面优化了模糊测试策略，以执行最佳的路径转换序列。如图2所示，它由四个组件组成。

图2 DeepGo的概述图

    定向灰盒模糊测试组件（DGF组件）会持续对种子进行变异，以生成用于到达目标位置的输入。该组件包含静态分析器和模糊测试器。在编译时，静态分析器计算基本块级别的距离（BB距离），记录每个分支的兄弟分支，并对目标程序进行插桩。一旦模糊测试启动，模糊测试器会持续对种子进行变异以测试程序。值得注意的是，路径转换模型也被集成到DGF组件中。

    虚拟集成环境（VEE）用于预测潜在的路径转换及其相应的奖励。VEE由深度神经网络（DNN）组成，并与模糊测试的强化学习组件共享历史回复缓冲区和预测回复缓冲区。历史回复缓冲区和预测回复缓冲区都是存储四元组的数据缓冲区，即（path, action, next_path, reward）。对于给定的四元组（path, action），训练好的VEE会根据不同路径转换的概率预测该动作的next_path和reward，表示为（next_path, reward）。

  

    强化学习模糊测试模型（Reinforcement Learning for Fuzzing Model）。该模型利用强化学习模型将历史路径转换和预测路径转换结合起来，以学习最大化序列奖励的策略。RLF模型由行动者网络（Actor network）、Q-评估网络（Q-Critic network）和V-评估网络（V-Critic network）组成。经过训练后，Q-评估网络可以评估每个动作造成的期望序列奖励, V-评估网络可以评估每个路径的转换值, 而行动者网络可以学习策略 𝜋 以最大化序列奖励。

    模糊测试优化组件（Fuzzing Optimization Component）。该组件通过优化模糊测试策略来实现最佳路径转换序列的执行。基于动作组，我们可以全面优化模糊测试的关键步骤，并使用多元素粒子群优化算法（Multi-elements Particle Swarm Optimization）同时优化动作组的各个元素。

    每个模糊测试周期大约持续 20 分钟。在每个模糊测试周期中，DeepGo 需要执行四项任务，包括：（1）使用模糊测试工具测试程序并提供历史路径转换以训练 VEE 和 RLF 模型；（2）VEE 提供预测的路径转换以训练 RLF 模型；（3）RLF 向 FO 组件提供转换值、期望序列奖励和策略；（4）FO 组件使用 MPSO 算法优化动作组，并将优化的模糊测试策略提供给 DGF。在 DeepGo 完成这四项任务后，它将进入下一个模糊测试周期并重复这四项任务。

B. 虚拟集成环境（Virtual Ensemble Environment）

    为了设计一种可以引导模糊测试器走向最优路径的策略，模糊测试器必须获得由路径中采取的动作引起的所有路径转换的奖励。然而，模糊测试器无法在有限的时间预算内（例如，24小时）在所有路径中采取所有动作。为了预测尚未采取的动作可能导致的路径转换和奖励，我们设计了虚拟集成环境（VEE），以模拟路径转换模型并预测潜在的路径转换及其相应的奖励。

    1）输入和输出编码：在训练VEE之前，我们应对path、action、reward进行编码。我们设计了虚拟集成环境（VEE）的编码方法，主要有两个目的。首先，VEE根据已探索路径中记录的路径转换预测新路径的潜在路径转换。其次，为了提高VEE的训练效率，我们需要使用低维向量来表示路径和动作。例如，将trace_bits映射到65536维的向量来表示路径会显著减慢深度神经网络（DNN）的训练速度。因此，在确保不同路径和动作可以清晰区分的同时，我们努力使用低维向量来表示路径、动作和奖励。

    路径。我们应用了耦合数据嵌入（CDE）算法[20]将AFL中用trace_bit表示的路径编码为一个20维的连续向量，并对每个维度的值进行归一化。CDE用于将离散向量表示为连续向量，同时保留区分路径的主要特征。根据CDE的方法，20维向量可以区分不同路径的主要特征，同时降低路径的维度，以提高深度神经网络（DNN）的训练效率。如果两个路径用trace_bits表示得更相似，则对应的20维向量之间的欧几里得距离会更接近。

    动作。我们根据变异位置对动作进行编码。以图1中的例子为例，种子s1的长度为100字节，如果模糊测试器选择s1的第4个字节作为变异位置，无论选择哪个变异器，模糊测试器都会从第4个字节开始变异s1，那么该动作的编码为4/100=0.04。所有动作的值也都进行了归一化处理。

    奖励是一个标量，根据公式 7 进行计算。

    采用这种编码方法，VEE 可以基于历史模糊测试信息预测潜在路径转换的概率和奖励。VEE 的训练数据包括四元组，即 (路径, 动作, 下一个路径, 奖励)，其中“动作”表示可以发生突变的种子字节，而不是具体的突变。因此，相同的动作（即相同的字节）使用不同的变异器会导致不同的路径转换和不同的概率。通过分析对一个字节进行突变的历史信息，VEE 可以预测采取这一动作（即用不同的变异器突变该字节）所导致的路径转换。对于已经进行过突变的字节，我们使用 VEE 预测通过不同变异器突变该字节所导致的不同路径转换的概率和奖励。对于尚未进行突变的种子或字节，我们使用具有相似结构的种子或具有相似偏移的字节来预测突变动作导致的路径转换的概率和奖励。这种相似性是通过 CDE 编码方法来测量的。如果两个种子表示的 20 维向量之间的欧几里得距离较短，则说明这两个种子更加相似。此外，在一个种子内部，两个动作的相似编码值表明它们对应字节的偏移量相似。

    2）VEE的训练：我们使用深度神经网络（DNN）构建VEE，以模拟路径转换模型中的路径转换行为。形式上，令 f:(path,action)→(next_path,reward) 表示DNN，它以四元组（路径，动作）为输入，输出四元组（下一个路径，奖励）。我们用 𝜃表示DNN的可训练权重参数，并使用一组训练样本 (X,Y) 来训练DNN，其中 𝑋表示输入集合，𝑌表示对应的输出集合。在路径转换模型中，由于相同的动作在相同路径上可能会以不同的概率导致不同的路径转换，路径转换模型本质上是一个概率模型。因此，在设计DNN f:(path,action)→(next_path,reward) 和损失函数时，我们主要处理VEE的随机性不确定性（aleatoric uncertainty）和认识性不确定性（epistemic uncertainty），以提高其预测的准确性。

    随机性不确定性（Aleatoric uncertainty）来源于模糊测试中路径转换的不可预测性。例如，在相同的突变位置使用不同的突变器可能会导致不同的路径转换。为了捕捉这种随机性不确定性，我们使用高斯概率分布来预测不同路径转换及其对应奖励的概率。这些路径转换和奖励是由路径 𝑝𝑡中的动作 𝑎𝑡引发的。我们通过可训练的权重参数来表示下一个路径 𝑝𝑡+1  和奖励 𝑟𝑡 的高斯概率分布，可以根据输入四元组 (𝑝𝑡,𝑎𝑡)进行表示：

其中，N代表高斯分布，代表高斯分布的均值；代表方差，指示均值的不确定性。我们定义了损失函数，用于衡量DNN输出与训练集中真实标签 𝑦∈𝑌之间的差异：

训练任务的目标是找到DNN函数 𝑓的权重参数 ，以最小化损失函数。

    认知不确定性（Epistemic uncertainty）源于大多数深度神经网络（DNN）采用的随机采样方法。由于单个DNN无法涵盖所有的训练数据，可能存在一些区域DNN无法准确预测输出，表现为认知缺陷。为了解决这一问题，我们采用了轨迹采样的概率集成算法（PETS），通过将多个DNN聚合到一个虚拟集成环境中来捕获认知不确定性。我们使用相同的随机采样方法，通过从历史回放缓冲区中采样四元组来训练DNNs。所有DNN生成的输出都表示为高斯概率分布，并通过加权这些结果，得出最终预测。该预测可表示为：

其中，n表示虚拟集成环境（VEE）中的深度神经网络（DNN）数量。考虑到训练速度、GPU内存限制以及VEE的预测准确性，我们使用6个相同的DNN构建VEE，并将6个DNN输出的概率平均值作为模型预测。通过对所有DNN的加权平均，可以减轻由于单个DNN在特定区域随机采样带来的认知缺陷。

    3）确定预测分布中的路径转换：给定输入 (pt, at)，神经网络输出潜在的路径转换及其相应的奖励，表示为 (pt+1, rt)，这采用高斯概率分布。然而，在定向模糊测试（DGF）中，种子的突变只会导致特定的路径转换。因此，我们使用随机采样方法，根据不同路径转换的预测概率来确定下一个路径 pt+1。

C. 用于模糊测试的强化学习模型

    为了更有效地引导模糊测试器朝向目标站点，即通过高奖励的路径转换序列，我们需要学习一种策略来选择动作，以最大化序列奖励。由于路径、动作和路径转换的数量庞大，使用传统的数学方法（如动态规划）来学习策略和计算期望序列奖励变得困难。因此，我们开发了用于模糊测试的强化学习（RLF）模型，该模型基于强化学习算法Soft Actor-Critic（SAC）。

    1）RLF模型的设计：如图2所示，RLF模型遵循SAC的结构，包含一个演员网络、一个Q评论家网络和一个V评论家网络。在训练过程中，我们训练Q评论家网络来评估期望的序列奖励，并训练V评论家网络来评估每条路径的转换值。通过获得期望的序列奖励和转换值，演员网络被训练以优化策略，从而提高选择高期望序列奖励动作的概率。

    2）训练数据处理和收集：我们将路径转换模型视为强化学习中的环境，并将fuzzer, path, action, path transition和 reward映射到强化学习中的agent, state, action, state transition和reward。此外，RLF重用VEE的路径、动作和奖励的编码方法。由于我们结合历史路径转换和预测路径转换来训练RLF，以赋予RLF模型前瞻性，因此我们以不同的方式收集历史路径转换和预测路径转换。

    收集历史路径转换。由于DGF的环境与传统强化学习过程（在该过程中状态转换是串行生成并表示为(s0, a0, s1, a1, ..., an-1, sn)）不同，因此RLF的训练数据处理方式也与传统强化学习（例如SAC）不同。在DGF中，模糊测试器可能多次变更一个种子，从而导致同一路径产生不同的路径转换。这意味着模糊测试器可能停留在某一特定路径上，并采取不同的行动以引起不同的路径转换。因此，对于RLF模型来说，在短时间内（例如几秒钟内）获取完整的路径转换序列并通过计算其序列奖励来评估当前策略的有效性是不可行的。基于这一考虑，在每个模糊测试周期中，模糊测试器根据策略选择行动以引起路径转换。历史路径转换被存储在历史重放缓冲区中，并在模糊测试周期结束时由RLF模型加载，以便在下一个模糊测试周期中训练RLF。

    收集预测路径转换。我们使用VEE来模拟路径转换模型，并采用k步分支回滚策略来获取尚未发生的预测路径转换。在k步分支回滚策略中，RLF模型被视为代理，并根据初始策略在每个路径上选择一系列动作，以引起k次路径转换，从而生成一个新的k长度路径转换序列。我们用图3来说明k步分支回滚策略的过程。假设(p0, a0, p1, a1, ... pi, ai, ... an-1, pn)是路径转换模型中的一个历史路径转换序列。我们以pi作为起点，并使用RLF的策略π选择一系列动作a′i, a′i+1, ..., a′i+k−1，引起k次路径转换，生成一个新的k长度路径转换序列，表示为(pi, a′i, ri, p′i+1), (p′i+1, a′i+1, r′i+1, p′i+2), ..., (p′i+k−1, a′i+k−1, r′i+k−1, p′i+k)。这里，k是一个超参数，会影响VEE预测的准确性和RLF模型设计策略的前瞻性。

图3 k步回滚策略

    在k步分支回滚过程中，预测可能需要覆盖多个测试用例。在不同的测试用例中，由字节位置定义的相同动作可能会出现错位（即，一个测试用例中被变异字节的位置可能与其他测试用例中的变异字节位置不一致，这是由于测试用例的长度不同造成的）。为了解决这种错位问题，我们使用变异ID ∧ (路径ID >> 2) 来区分在此过程中生成的不同中间测试用例。例如，对于覆盖相同路径的测试用例1和测试用例2，我们仍然为它们分配不同的ID，这样可以区分不同中间测试用例上的变异。通过这种方式，即使测试用例1和测试用例2的相同字节被变异，我们也不会认为这两个变异所导致的路径转换的概率和奖励是相同的。

    3) RLF模型的训练：RLF模型结合历史路径转移和预测路径转移来训练Actor网络、Q-Critic网络和V-Critic网络。在DGF中，我们希望模糊测试器采取具有高期望序列奖励的动作，同时也探索不同的动作以引起新的路径转移。因此，在RLF中，我们应用熵来衡量选择动作的随机性。假设我们根据策略π在状态st中选择动作，选择动作的概率遵循一个称为π(·|st)的分布，则动作的熵计算如下：

在RLF模型中，演员网络的目标是学习到一个策略π*，以最大化奖励和熵。

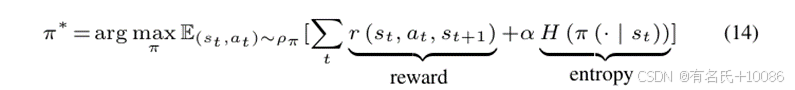
其中，α是一个平衡探索和开发的系数，如SAC中所提出的。然后，我们构建Q-Critic网络的目标函数和V-Critic网络的目标函数，以训练Q-Critic网络的参数ω和V-Critic网络的参数ϕ。

对于Actor网络，我们训练Actor网络的参数σ，以最大化动作的期望序列奖励，从而最大化序列奖励。

通过最小化这三个目标函数，我们训练三个网络中的参数，以计算期望序列奖励和转移值，并设计选择动作的策略，以最大化序列奖励。训练良好的RLF模型为FO组件提供两种类型的优化信息：（1）估计的期望序列奖励和估计的转移值，以及（2）在每条路径中选择动作的策略。

D. 基于动作组优化模糊测试策略

    为了引导模糊测试器执行具有最高序列奖励的最佳路径转换序列，我们需要基于RLF模型的反馈信息来优化模糊测试策略。近年来，已经提出了一些先进技术来优化单一的模糊测试策略，例如种子选择、变异调度和变异位置选择。然而，仅优化单一的模糊测试策略可能无法显著引导模糊测试器朝向最佳路径转换序列。因此，我们提出了由五个元素组成的动作组的概念，并试图全面优化多个模糊测试策略。此外，我们提出了多元素粒子群优化（MPSO）算法，以同时优化动作组中的各个元素。

    1）动作组的概念：我们将动作组定义为一个包含五个元素的元组。

·种子选择（记作 SS）：表示种子被模糊测试器选择进行模糊测试的概率。

·种子能量（记作 SE）：表示分配给种子的能量，决定在havoc阶段可以对该种子应用的变异次数。

·Havoc轮次（记作 HR）：表示在混乱阶段用于选择不同变异器和字节的循环轮次。所有选择的变异器和字节都整合为一个单一的混乱动作。混乱轮次的值可以为 2、4、8、16、32、64 或 128。

·变异器（记作 MT）：表示选择用于变异种子的变异器。与 AFL [24] 类似，DeepGo 保留了 16 种不同类型的变异器。

·位置（记作 LC）：表示选择用于变异的种子的变异位置。

    每个动作组表示为一个包含 5 个元素的 27 维向量。如图 4 所示，种子选择（SS）和种子能量（SE）都是 1 维向量。SS 的值表示范围在 [0, 1] 内的概率，模糊器根据 SS 选择种子进行模糊测试。SE 的值表示分配给种子的能量，模糊器根据 SE 计算种子的变异次数。混乱轮次（HR）是一个 7 维向量，其中每个维度表示选择七个不同混乱轮次值（即 2、4、8、16、32、64 和 128）之一的概率。模糊器根据 HR 采样用于选择不同变异器和变异位置的循环轮次数量。变异器（MT）是一个 16 维向量，其中每个维度表示选择 16 种不同类型变异器之一的概率。位置（LC）是一个 2 维向量，其中第一个维度表示选择最佳位置的概率，第二个维度表示选择常见位置的概率。我们将种子的变异位置分为两个类别：最佳位置和常见位置。最佳位置包括由 RLF 模型的策略选择的概率大于 80% 的变异位置，而常见位置则包括所有其他变异位置。根据 MT 和 LC，模糊器采样变异器和变异位置的类型。模糊器不断根据动作组中的五个元素变异种子以生成新输入。如图 4 所示，我们将每个元素表示为一个向量，并将这五个向量连接成一个向量，以表示种子的动作组。

图4 动作组元素的布局

    2）多粒子种群优化算法：为了同时优化动作组中的五个元素，我们将每个动作组视为由 27 维向量表示的粒子，并将动作组的优化视为一个多元素优化问题。我们提出了一个多元素粒子群优化算法（即 MPSO）来实现这种优化。通过优化动作组，可以引导模糊器朝向具有高序列奖励的目标路径转换序列。

    正如我们在第 II 节中介绍的，粒子群优化 (PSO) 算法使用无质量的粒子来模拟鸟群中的鸟。每个粒子单独搜索最优解，并将其记录为局部最优值。然后，这些局部最优值在整个群体中的粒子之间共享，以找到全局最优值作为最优解。这些粒子有两个主要属性：速度和位置。速度代表移动的速度，位置代表移动的方向。群体中的所有粒子都会根据共享的局部最优值和全局最优值不断调整它们的速度和位置：

其中，𝑣𝑖代表第 𝑖个粒子的速度，𝑥𝑖代表第 𝑖个粒子的位置，r 代表在 [0,1] 范围内的随机位移权重，lbesti代表第 𝑖个粒子找到的局部最优位置，而gbesti 代表所有粒子找到的全局最优位置。惯性因子 𝜔是一个非负值，较大的值会使 PSO 算法的全局优化能力更强，而局部优化能力更弱。本文中，我们采用线性递减惯性权重（LDIW）方法来设置 𝜔的值，具体为：

其中，

𝜔𝑖𝑛𝑖 和 𝜔𝑒𝑛𝑑分别表示初始惯性值和最终惯性值。按照线性递减惯性权重（LDIW）的设定𝜔𝑖𝑛𝑖和𝜔𝑒𝑛𝑑通常被设定为 0.4 和 0.9。变量 𝑔表示当前粒子完成的迭代次数，即模糊测试器对相应种子执行的变异次数。而 𝐺表示最大迭代次数，即根据种子能量计算出的总变异次数。在 DeepGo 中，种子的变异次数由分配给种子的能量决定。   

        局部最优位置和局部效率。在MPSO算法中，每个粒子都有其局部最优位置和局部效率。对于给定的粒子，当该粒子在位置 𝑥1  的局部效率高于在位置 𝑥2  时，位置

𝑥1被认为优于位置 𝑥2。我们使用局部效率来量化一个特定粒子的模糊测试策略的变异效率，这些策略由五个元素组成。局部效率是根据模糊测试器在该粒子对应路径上的所有变异所产生的平均期望序列奖励来计算的。在DGF中，每次对种子的变异都会导致从路径 𝑝到路径 𝑝′的路径转换。根据公式 (5)，使用 来评估单次路径转换的期望序列奖励。基于此，我们计算局部效率。

其中，表示第𝑖次变异覆盖路径 𝑝′的路径转换值。

    全局最优位置和全局效率。我们使用全局效率来量化模糊器的模糊测试效率。由于模糊器的全局效率取决于不同粒子的局部效率及其相互关系，我们根据模糊测试周期内的模糊测试效率确定所有粒子的全局位置。如果某个粒子的模糊测试效率高于其他任何位置，则该粒子当前处于全局最优位置（gbest）。我们通过模糊测试周期内的平均序列奖励来评估全局效率：

其中，effglobal 表示全局效率，sj 表示第 j 个种子，gj 表示该种子的总变异次数，U 表示在当前模糊测试周期中被测试的种子数量。

    在模糊测试过程中，我们根据公式 (21) 和 (22) 计算粒子的局部效率和全局效率，并记录 lbest 和 gbest。然后根据公式 (18)、(19) 和 (20) 更新粒子的空间位置，将所有粒子朝着 lbest 和 gbest 的方向移动。通过这种方法，我们优化所有种子的操作组，以引导模糊测试工具通过最优路径转换序列到达目标。

    MPSO 的过程如算法 1 所示，其中s表示种子，p表示粒子，Ω(s, p) 表示包含所有种子及其对应粒子的集合。函数 Prob_Sels 根据 SS 决定是否对种子进行模糊测试。mni 表示种子的变异次数，函数 Cal_MN 基于 SE 计算种子的变异次数。函数 Prob_Selh、Prob_Sell 和 Prob_Selm 分别根据 HR、LC 和 MT 概率选择 hr（havoc 轮次）、lc（变异位置）和 mt（变异器）。

算法1 MPSO算法

    首先，我们初始化所有粒子的五个元素（第 1 行）。对于 SS 和 SE，根据种子的特性（如位图大小和执行速度），AFL [24] 计算种子被模糊测试的概率以及分配给种子的能量。我们使用 AFL 方法获得的概率和种子能量作为 SS 和 SE 的初始值。对于 HR、LC 和 MT，我们使用其空间位置的平均概率作为初始值（例如，每个变异器为 1/16）。在模糊测试过程中，fuzzer 根据 SS 选择种子进行测试（第 4 行），根据 SE 计算变异次数（第 5 行），选择 HR 的值（即 hrj）（第 7 行），根据 LC 选择种子字节进行变异（即 lck）（第 9 行），并根据 MT 选择变异器（即 mtk）（第 10 行）。在每个 hrj 循环中，mtk 和 lck 将结合成一次 havoc 变异（即 hmj）（第 11 行），fuzzer 将使用 hmj 对种子 si 进行变异并生成新的输入（第 13 行）。然后，MPSO 将计算局部效率和全局效率（第 14 行），并更新 lbest、gbest 以及粒子 pi 的位置（第 15 行）。值得注意的是，粒子的所有维度值将根据公式 (18)、(19) 和 (20) 不断变化，更新粒子的空间位置，使其向 lbest 和 gbest 移动。例如，如果一个粒子具有较低的局部效率，导致 fuzzer 的全局效率下降，根据公式 (18)、(19) 和 (20)，SS 和 SE 在 MPSO 过程中将逐渐减少。一旦 FO 组件首次接收到来自 RLF 模型的反馈信息，它将启动 MPSO 算法，直到模糊测试结束。

5 实现

    DeepGo 的实现主要包括三个组件：fuzzer、VEE 和 RLF 模型。对于 fuzzer 中的静态分析器，我们利用了 LLVM 11.0。我们使用 LLVM IR 来插装程序并获取基本块级别的距离、兄弟分支等信息。fuzzer 基于 AFLGo 构建，使用了 2100 行的 C 代码，而 VEE 和 RLF 模型则使用了约 1300 行的 Python 代码实现。

    具体来说，VEE 的深度神经网络（DNNs）使用 Pytorch 1.13.0 实现，包含五个全连接层。隐藏层使用 Swish 作为激活函数。DNNs 训练了 500 个 epoch，并使用 tensorboard 工具自动监控损失值，以确定它们是否收敛到较小的值。如果 VEE 和 RLF 的损失值已经收敛，DNNs 将自动停止训练。RLF 模型中的网络由三层全连接层组成。关于 RLF 模型的超参数，参考了 SAC 中 Q-Critic、V-Critic 和 Actor 网络的学习率设置，我们将其设置为 0.005，以确保 RLF 模型的学习效率和收敛性（在实验过程中，三个网络都能快速收敛）。

    值得注意的是，在使用 DeepGo 测试程序时，模糊测试过程、模型训练和路径转换预测是同时进行的。我们使用额外的 GPU 来基于模糊测试过程中收集的信息训练 VEE 和 RLF 模型。所有用于 VEE 和 RLF 模型的训练和预测时间都包含在模糊测试过程的时间预算中（即clock时间）。

7 讨论

    超参数的设置。超参数 𝛾和 𝑘都会影响 DeepGo 的 TTR（时间到达率，Time-to-Reach）。首先，在 RLF 模型的训练中，超参数 𝛾用于平衡当前奖励和后续奖励对当前状态及其动作的转换值和期望序列奖励的影响。如果只关注当前奖励，RLF 可能会陷入局部最优；而过度强调后续奖励，可能会导致当前路径上的低奖励路径转换，从而降低定向效率。因此，超参数 𝛾的设置会影响 RLF 模型的 Q 值、V 值和策略，进而影响 DeepGo 的 TTR。其次，在 k 步分支展开策略中，超参数 𝑘用于生成 k 长度的路径转换序列。随着 𝑘的增加，VEE 能够预测更多的路径转换，从而使 RLF 在设计策略时具有更强的前瞻性。然而，过高的 𝑘值可能会导致 VEE 预测路径转换和奖励的准确性下降，误导 RLF 的策略进入低奖励的路径转换序列。因此，超参数 𝑘的设置会影响 VEE 的预测准确性和 RLF 策略的前瞻性，最终影响 DeepGo 的 TTR。

    为了观察不同 𝛾和 𝑘对 DeepGo 的影响，我们在实验中将 𝛾设置为 0.9、0.8、0.7、0.6、0.5、0.4、0.3、0.2 和 0.1，将 𝑘 设置为 1 到 9，使用不同超参数配置的 DeepGo 测试了 UniBench 中的 20 个程序，并记录了每个测试用例的平均 TTR（时间到达率）。为了直观展示 𝛾和 𝑘设置对 DeepGo 的 TTR 影响，我们使用 3D 图表展示了 TTR 随着 𝛾和 𝑘变化的情况。根据图 9，可以得出以下三点结论：

·当 𝛾设置为 0.8 且 𝑘设置为 4 时，TTR 达到最小值，图中标记为红点。

·如果 𝛾 值在 [0.5, 0.9] 范围内，且 𝑘值在 [3, 5] 之间，𝛾和 𝑘对 TTR 的影响相对较小（TTR 的变化范围在 [648, 688] 之间）。

·当 𝛾大于 0.5 时，TTR 较高；当 𝑘小于 5 时，TTR 较高。这表明，由于基于统计模糊信息，模糊测试中的路径转换序列长度通常小于 20，因此我们应更多关注路径当前奖励的影响。此外，𝑘 的设置应平衡预测和前瞻性，选择一个合适的值。

图9超参数对TTR的影响

    选择目标。在选择评估目标时，我们运行了 AFL++ 48 小时，因为我们认为定向模糊测试（DGF）技术能够比传统覆盖导向模糊测试（CGF）技术更快地到达预定义目标。因此，即使某些目标是由 CGF 在 24 到 48 小时内达到的，我们仍然相信 DGF 能够在 24 小时内到达这些目标。例如，在我们的评估中，AFL++ 花费超过 24 小时到达的 51 个目标中，有 45 个被一个或多个定向模糊测试工具在 24 小时内到达。我们选择使用 AFL++ 而非“常规”的 AFL 来设置这些目标，是因为 AFL++ 提供了更全面的结果，能够详细记录 CGF 达到不同目标所需的时间。通过 AFL++ 提供的信息，我们可以重现代码位置以及到达这些位置的时间成本，而这对于我们选择目标是必要的。相比之下，AFL 并没有提供如此详细的信息。

8相关工作

    定向符号执行（DSE） 主要依赖符号执行引擎，例如 KLEE [7]、KATCH [33] 和 BugRedux [2]，来到达目标位置。通过程序分析和约束求解，DSE 可以生成有效穿透路径约束并指向目标位置的输入。尽管一些最新的研究成果（如 symcc [40]、symqemu [39] 和 JigSaw [9]）致力于改进符号执行，但 DSE 的重量级程序分析、路径爆炸问题以及约束求解仍然限制了其可扩展性。

    定向灰盒模糊测试（DGF） 通过计算种子与预定义目标之间的距离，优先处理接近目标的种子，将可达性问题转化为一个优化问题，以最小化种子与目标之间的距离。基于 AFLGo 的思想，Hawkeye [8]、LOLLY [29]、Berry [28]、UAFL [50] 和 CAFL [25] 提出了新的适应性度量标准，如轨迹相似性和序列相似性，以增强定向性并检测难以发现的漏洞。FuzzGuard [59] 通过筛除不可达的种子，BEACON [18] 通过修剪不可行的路径，有效地提高了 DGF 的效率。MC2 [43] 将 DGF 建模为一个由预言机引导的搜索问题，旨在加速找到可达目标的输入。FISHFUZZ [58] 使模糊测试工具能够在数千个目标之间无缝扩展并优先处理有趣的种子，从而实现更全面的程序测试。SemFuzz [12], [54] 分析数据流信息和语义信息，以生成有效的输入。Parmesan [37]、V-Fuzz [37] 和 SAVIOR [10] 利用 ASAN [42] 和 UBSan [30] 等工具，将潜在的错误代码标记为目标位置，并引导 DGF 测试这些位置。Hydiff [23]、SAVIOR [10] 和 Badger [36] 优先处理可能导致特定程序漏洞位置的种子，然后优先对那些可从多个目标位置到达的种子进行符号执行。DrillerGO [22] 和 Berry [28] 结合了 DSE 的精确性和 DGF 的可扩展性，以弥补各自的不足。然而，DGF 仍然面临难以穿透难以满足的路径约束的问题。DeepGo 通过预见关键的执行信息并预测最佳路径，结合历史执行信息与未来执行信息，智能生成最佳且可行的路径到达目标位置，避开不可行和难以执行的路径，从而更加精确和高效地到达目标位置。

    基于AI的灰盒模糊测试：以往的前沿工作 [14], [45], [48], [49], [51], [59] 应用AI技术来增强灰盒模糊测试技术。在这些工作中，NEUZZ [45] 和 MTFUZZ [44] 引入了基于梯度下降的方法，通过近似被测程序（PUT）的离散分支行为来增强覆盖引导的灰盒模糊测试。AthenaTest [49] 使用基于局部Transformer的网络从语料库中提取种子的特征并生成测试用例。DYNFuzz [57] 和 FuzzGuard [59] 基于神经网络建立模型，预测种子是否可到达目标位置，并筛选出不可达的种子以增强定向性。然而，现有的基于AI的灰盒模糊测试技术仅优化了突变字节或种子的选择，无法全面优化所有模糊测试策略，这使得模糊测试工具在生成到达目标位置的最佳路径时显得不够智能。

9 结论

    本文提出了DeepGo，一种预测性定向灰盒模糊测试工具，能够结合历史信息和预测信息引导定向灰盒模糊测试（DGF）通过最佳路径到达目标位置。DeepGo 构建了虚拟集成环境（VEE），使用深度神经网络（DNNs）模拟路径转换模型并预测潜在路径转换的奖励值。通过强化学习模型（RLF），DeepGo 结合历史和预测的路径转换，确定具有最高序列奖励的路径转换序列，以生成最佳路径。基于多粒子群算法（MPSO），DeepGo 优化了动作组并执行高奖励的路径转换序列，实现最佳路径。我们在25个实际程序中的100个目标位置上评估了DeepGo，实验结果表明，DeepGo在到达目标位置并暴露已知漏洞方面，优于当前最先进的定向模糊测试工具（如AFLGo、BEACON、WindRanger和ParmeSan）。此外，DeepGo 在预测尚未经过的路径转换方面也表现出较高的准确性。