20221122 排序算法总结_2022-12-1, 2022-2-1,降序排序-CSDN博客

本文介绍了四种基本排序算法：选择排序、冒泡排序、插入排序和快速排序。详细讲解了每种算法的实现逻辑、时间复杂度和稳定性，并通过示例代码进行演示。选择排序的时间复杂度为O(n^2)，冒泡排序在最好情况下达到O(n)，插入排序在最佳情况也是O(n)，而快速排序平均时间复杂度为O(nlogn)。

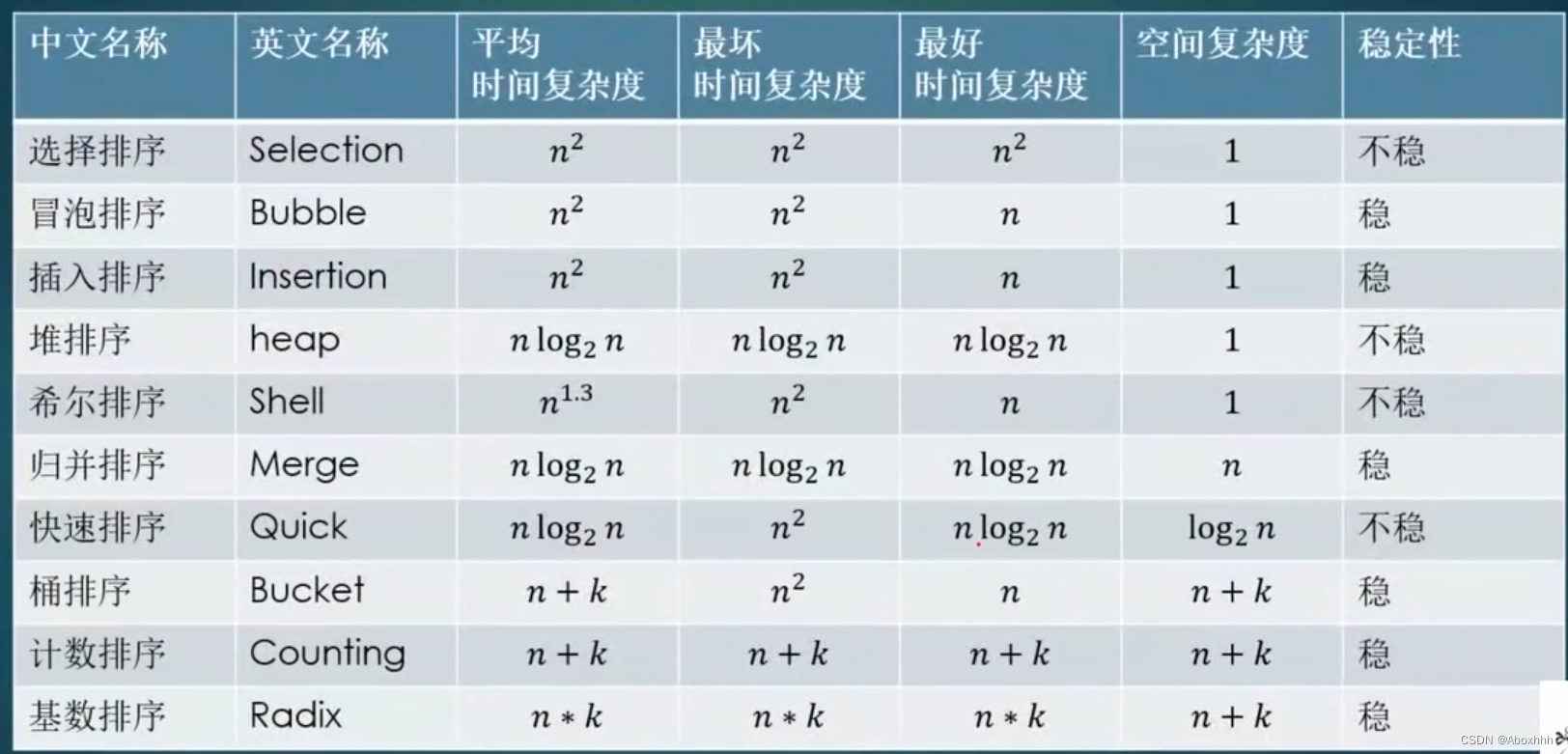
在这里插入图片描述

选泡插，
快归堆希统计基，
恩方（最上面三种）恩老恩（快归堆）13（希），
对恩+k（统计）恩乘k（基）。

程序编写逻辑

简单到复杂
局部到整体
粗糙后精细

选择排序

O(n^2) 而且不稳定

思路
遍历数组从第1个开始，
找到最小值放第1个位置（交换过程）
然后从第2个开始，找到第2个之后最小值放第2个位置
然后从第3个开始，找到第3个之后最小值放第3个位置
……
依次遍历

        for (int i = 0; i < arr.length-1; i++) {
            int minPos=i;

            for (int j = i+1; j < arr.length; j++) {
                if(arr[j]<arr[minPos]){
                    minPos=j;
                }
            }
            // find the min and change position
            swap(arr,i,minPos);
            System.out.println("The "+(i+1)+" time exchange!");
            print(arr);

        }

冒泡排序

空间复杂度：O（1）–不涉及额外的空间
时间复杂度：O（n^2）
最好的时间复杂度可以达到：O（n）
稳定

每次都从数组的第一个数开始，和后面的比较
比后面的大就放后面
没有后面的大就不动
总结本质：
就是n-1个循环，找前n个到1个的最大值放在前n~1个的最后位置。

 for (int j=1;j< a.length-1;j++){
           //这一层循环决定了最大的数字放在倒数第几个
           for (int i = 0; i <a.length-j ; i++) {
               if(a[i]>a[i+1]){
                   swap(a,i,i+1);
               }

           }
           print(a);
       }
       /*   12 5 3 4 2 8 1 7 0 11 
   			5 3 4 2 8 1 7 0 11 12 
   			3 4 2 5 1 7 0 8 11 12 
   			3 2 4 1 5 0 7 8 11 12 
   			2 3 1 4 0 5 7 8 11 12 
   			2 1 3 0 4 5 7 8 11 12 
   			1 2 0 3 4 5 7 8 11 12 
   			1 0 2 3 4 5 7 8 11 12 
   			0 1 2 3 4 5 7 8 11 12 

       */

插入排序

空间复杂度：O（1）
时间复杂度：O（n^2）最好的时候O（n）

思想就是把已经排好的放到前面，每次后面乱序的往前面拍好的部分插入。
在这里插入图片描述
优化就是在交换的过程中
直接把大于第i个的数字往后移动
a[j]=a[j-1]

for (int i = 0; i < arr.length; i++) {
            for (int j = i; j >0; j--) {
                if(arr[j]<arr[j-1]){
                    swap(arr,j,j-1);
                }
            }
        }

以上就是三种简单排序
冒泡相对来说太慢
选择不太稳

快速排序

找一个pivot首先
给数组从左到右的遍历
大于pivot的放在左边
小于pivot的放在右边
然后递归
不断地二分
因此这个复杂度就是logn
然后每一层都会遍历
所以就O（nlogn）

在这里插入图片描述

普通快拍举例说明：
以7作为pivot
先看1 ，4,6都比7小，不动
9比7大，就放在7前面一个的位置（8）处
10比7大，就放在前两个的地方（5）处
然后2,3,5均比7小。就不动了
把7放在中间的位置
第一次二分结束
经典快拍说明：
1.pivot确定（选取最右端）
2.从左往右找比piv大的，从右往左找比piv小的，直接做交换

        while(left<=right){
            while (left<=right&&arr[left]<=pivot) left++;
            while (left<=right&&arr[right]>pivot) right--; //精髓了 先判断再执行 避免了越界
            print(arr);
            if(left<right){
                swap(arr,left,right);
            }
        }

        swap(arr,left,rightbound);