[Python]代码随想录Day17

654.最大二叉树

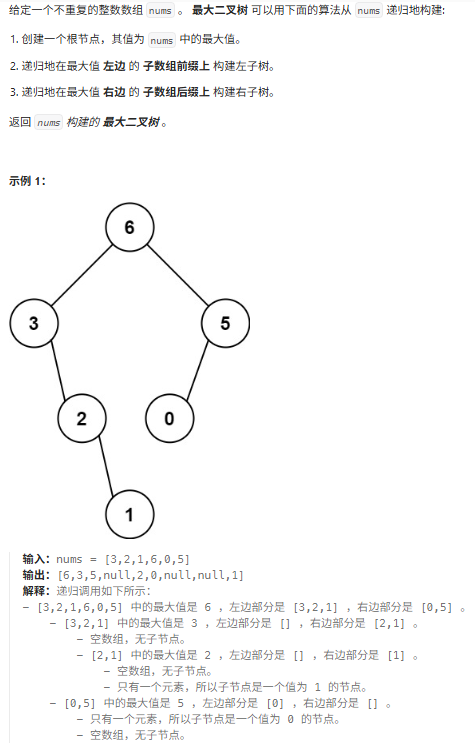
基础版

class Solution:
    def constructMaximumBinaryTree(self, nums: List[int]) -> TreeNode:
        if len(nums) == 1:
            return TreeNode(nums[0])
        node = TreeNode(0)
        # 找到数组中最大的值和对应的下标
        maxValue = 0
        maxValueIndex = 0
        for i in range(len(nums)):
            if nums[i] > maxValue:
                maxValue = nums[i]
                maxValueIndex = i
        node.val = maxValue
        # 最大值所在的下标左区间 构造左子树
        if maxValueIndex > 0:
            new_list = nums[:maxValueIndex]
            node.left = self.constructMaximumBinaryTree(new_list)
        # 最大值所在的下标右区间 构造右子树
        if maxValueIndex < len(nums) - 1:
            new_list = nums[maxValueIndex+1:]
            node.right = self.constructMaximumBinaryTree(new_list)
        return node

使用切片

class Solution:
    def constructMaximumBinaryTree(self, nums):
        if not nums:
            return None
        max_val = max(nums)
        node = TreeNode(max_val)
        max_index = nums.index(max_val)
        node.left = self.constructMaximumBinaryTree(nums[:max_index])
        node.right = self.constructMaximumBinaryTree(nums[max_index + 1 : ])
        return node

617.合并二叉树

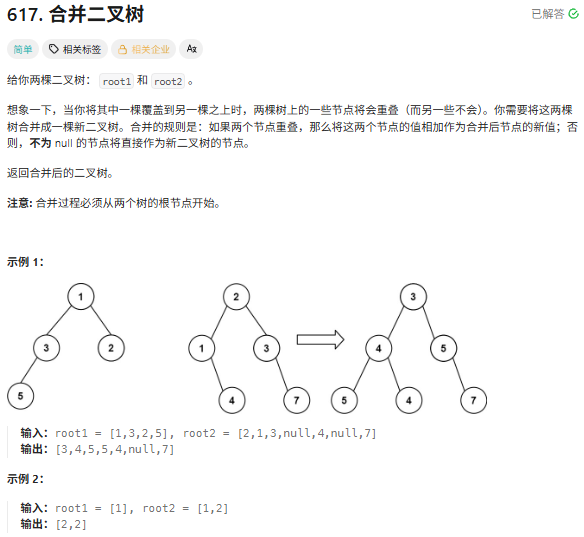
直接合并

class Solution:
    def mergeTrees(self, root1: Optional[TreeNode], root2: Optional[TreeNode]) -> Optional[TreeNode]:
        if root1 is None: 
            return root2
        if root2 is None:
            return root1
        # 下面是创造了一个新节点，也可以只合并在tree1里
        return TreeNode(root1.val + root2.val,
            self.mergeTrees(root1.left,root2.left), # 合并左子树
            self.mergeTrees(root1.right,root2.right)) # 合并右子树

前序直接合并，修改root1

class Solution:
    def mergeTrees(self, root1: TreeNode, root2: TreeNode) -> TreeNode:
        # 递归终止条件: 
        #  但凡有一个节点为空, 就立刻返回另外一个. 如果另外一个也为None就直接返回None. 
        if not root1: 
            return root2
        if not root2: 
            return root1
        # 上面的递归终止条件保证了代码执行到这里root1, root2都非空. 
        root1.val += root2.val # 中
        root1.left = self.mergeTrees(root1.left, root2.left) #左
        root1.right = self.mergeTrees(root1.right, root2.right) # 右
        
        return root1 # ⚠️ 注意: 本题我们重复使用了题目给出的节点而不是创建新节点. 节省时间, 空间.

层序迭代法

from collections import deque

class Solution:
    def mergeTrees(self, root1: TreeNode, root2: TreeNode) -> TreeNode:
        if not root1:
            return root2
        if not root2:
            return root1

        queue = deque()
        queue.append((root1, root2))

        while queue:
            node1, node2 = queue.popleft()
            node1.val += node2.val

            if node1.left and node2.left:
                queue.append((node1.left, node2.left))
            elif not node1.left:
                node1.left = node2.left

            if node1.right and node2.right:
                queue.append((node1.right, node2.right))
            elif not node1.right:
                node1.right = node2.right

        return root1

700.二叉搜索树中的搜索

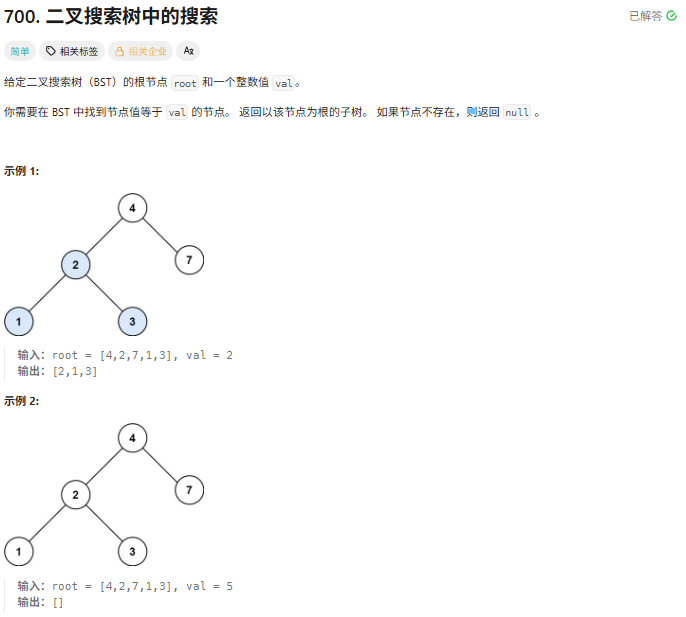
递归

class Solution:
    def searchBST(self, root: TreeNode, val: int) -> TreeNode:
        # 为什么要有返回值: 
        #   因为搜索到目标节点就要立即return，
        #   这样才是找到节点就返回（搜索某一条边），如果不加return，就是遍历整棵树了。

        if not root or root.val == val: 
            return root

        if root.val > val: 
            return self.searchBST(root.left, val)

        if root.val < val: 
            return self.searchBST(root.right, val)

迭代法

class Solution:
    def searchBST(self, root: TreeNode, val: int) -> TreeNode:
        while root:
            if val < root.val: root = root.left
            elif val > root.val: root = root.right
            else: return root
        return None

98.验证二叉搜索树

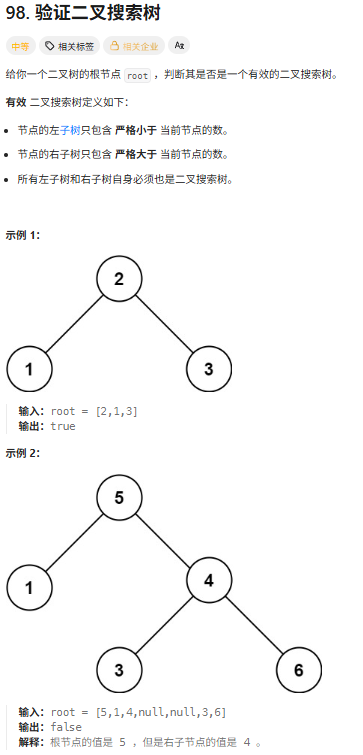
利用中序遍历，看看它的元素是不是有序 单调递增的 但是可以继续优化

递归

class Solution:

    def isValidBST(self, root: Optional[TreeNode],left = -inf, right= inf) -> bool:
        if root is None:
            return True
        x = root.val
        return left< x <right and self.isValidBST(root.left,left,x) and self.isValidBST(root.right,x,right)