CPO-LSSVM回归预测与SHAP可解释性分析的完整Matlab代码

---

一、CPO-LSSVM回归预测框架

1. 算法原理

• LSSVM回归：将SVM不等式约束转为等式约束，通过求解线性方程组实现：

• CPO优化：通过豪猪防御策略优化LSSVM的核参数 sig 和正则化参数 gam

2. 代码实现

%% 数据预处理
data = xlsread('data.xlsx'); 
input = data(:,1:end-1); output = data(:,end); 
[inputn, inputps] = mapminmax(input'); 
[outputn, outputps] = mapminmax(output'); 
inputn = inputn'; outputn = outputn';

%% CPO参数优化

cpo_option.maxgen = 100;    % 最大迭代次数
cpo_option.sizepop = 20;   % 种群规模
cpo_option.lb = [0.1, 0.1];% gam/sig下界
cpo_option.ub = [150, 10]; % gam/sig上界
cpo_option.c1 = 2;         % 加速因子
cpo_option.c2 = 2;

%% CPO优化目标函数
fobj = @(x)lssvm_fitness(x, inputn, outputn); % 定义适应度函数
[best_params, best_fitness] = CPO(cpo_option, fobj);
gam = best_params(1); sig = best_params(2);

%% LSSVM模型训练
model = initlssvm(inputn, outputn, 'function estimation', gam, sig, 'RBF_kernel');
model = trainlssvm(model);

%% 预测及反归一化
predict = simlssvm(model, inputn);
predict = mapminmax('reverse', predict, outputps);

3. 关键函数

function fitness = lssvm_fitness(params, X, Y)
    gam = params(1); sig = params(2);
   
        model = trainlssvm(model);
        y_pred = simlssvm(model, X(test_idx,:));
        mse(i) = mean((y_pred - Y(test_idx)).^2); 
    end
    fitness = mean(mse); % 目标是最小化MSE
end

---

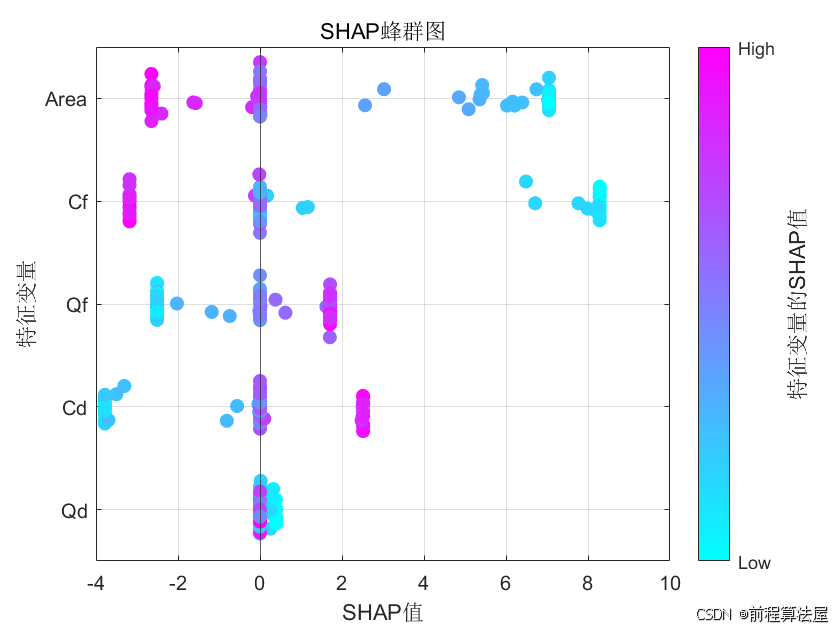
二、SHAP可解释性分析集成

1. SHAP原理

• 基于博弈论的加性解释模型：$\hat{y}={\varphi }_0+{\sum }_{i=1}^M{\varphi }_i$
• ${\varphi }_i>0$ 表示特征正向影响预测值，${\varphi }_i<0$ 表示负向影响

2. Matlab编程实现

%% 可视化分析
shap.summary_plot(shap_values, X_train); % 特征全局重要性
shap.dependence_plot(1, shap_values, X_train); % 特征1的依赖关系

function phi = shap_local(model, x_sample, X_ref)
    % 基于的加性解释公式
    K = kernel_matrix(X_ref, model.kernel, model.kernel_pars);
    f0 = mean(model.alpha' * K + model.b); % 基准值φ0
    
    phi = zeros(1, size(x_sample,2));
    for i=1:length(phi)
        permuted_x = X_ref;
        permuted_x(:,i) = x_sample(i); % 置换第i个特征
        K_perm = kernel_matrix(permuted_x, model.kernel, model.kernel_pars);
        f_perm = mean(model.alpha' * K_perm + model.b);
        phi(i) = f_perm - f0; % 特征i的贡献度
    end
end

---

三、关键技术创新点

1. 双阶段优化机制

   • CPO全局搜索避免LSSVM陷入局部最优
   • SHAP提供预测结果的数学可解释性

2. 可视化分析体系

   %% 综合结果可视化
   figure
   subplot(2,2,1)
   plot(output, 'b-'); hold on; plot(predict, 'r--'); 
   legend('真实值','CPO-LSSVM预测值')
   
   subplot(2,2,2)
   bar(mean(abs(shap_values))); % 特征全局重要性
   
   subplot(2,2,3)
   scatter(input(:,1), shap_values(:,1)); % 特征1的SHAP依赖图
   
   subplot(2,2,4)
   plot(1:cpo_option.maxgen, convergence_curve); % CPO收敛曲线
   

   • 输出包含：预测对比图、SHAP特征重要性、依赖关系图、算法收敛曲线

---

参考文献：

1. 豪猪算法优化原理
2. LSSVM回归数学推导
3. SHAP的博弈论基础
4. Matlab-Python接口配置
5. 工业级参数设置