黑龙江省赛 The 16th Heilongjiang Provincial Collegiate Programming Contest（2022 CCPC练习赛）

原创已于 2022-05-18 17:02:04 修改 · 1.7k 阅读

3 ·

CC 4.0 BY-SA版权

文章标签：

#蓝桥杯 #算法 #c++ #开发语言 #拓扑学

于 2022-05-18 10:14:58 首次发布

codeforces补题专栏收录该内容

17 篇文章

订阅专栏

本文介绍了如何使用区间动态规划解决一个涉及区间乘法的问题，并强调了预处理逆元的重要性，避免因取模后除法导致的时间复杂度提升。通过实例代码展示了如何计算逆元并将其应用于状态转移方程，以及为什么在某些场景中需要取逆元。

D. Doin' Time

思路：区间DP板子 + 求逆元，

注意：预处理逆元，否则TLE

忘记区间DP的点这里 -> 区间DP模板题（石子合并）

与石子合并不同的地方：

1，预处理不同，石子合并为区间和，此题为区间乘法

2，状态计算不同，石子合并为s[r] - s[l] ，此题目为，s[r] / s[l]

关于为什么取逆元的问题：

目的是：保持取模后的除法的结果与没取模的结果一样，

具体应用场景：数据很大，需要取模，同时取模过的数要做除法

如果不取逆元的错误举例

8/4%5 = 2，(8%5)/(4%5) = 0

8/4%5 == 8/qmi(4)%5 == 2

代码如下：

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;

const int N = 310, mod = 1000003;

int n;
LL s[N], ns[N], f[N][N];

LL qmi(int a, int k)
{
    LL res = 1;
    while(k)
    {
        if(k & 1) res = (LL)res*a%mod;
        k >>= 1;
        a = (LL)a*a%mod;
    }
    return res;
}

int main()
{
    scanf("%d", &n);

    s[0] = 1, ns[0] = 1;
    for(int i = 1; i <= n; i ++ )
    {
        scanf("%lld", &s[i]);
        s[i] = s[i] * s[i-1] %  mod;
        ns[i] = qmi(s[i], mod - 2)%mod;
    }

    for(int len = 2; len <= n; len ++ )
    {
        for(int i = 1; i + len - 1 <= n; i ++ )
        {
            int l = i, r = i + len - 1;
            for(int k = l; k < r; k ++ )
                f[l][r] = max(f[l][r], f[l][k] + f[k+1][r] + (s[r]*ns[k]%mod - s[k]*ns[l-1]%mod) * (s[r]*ns[k]%mod - s[k]*ns[l-1]%mod));
        }
    }

    printf("%lld\n", f[1][n]);

    return 0;
}

H Hack DSU

H - Hack DSU!

思路：

题目中的代码

#include <iostream>
using namespace std;
const int MAXN = 1e5+10;
int parent[MAXN];
long long counter = 0;

int find(int x) {
    while (x != parent[x]) {
        if (x < parent[x]) {
            // 路径压缩
            parent[x] = parent[parent[x]];
        }
        x = parent[x];
        counter++;
    }

    return x;
}

void merge(int a, int b) {
    a = find(a);
    b = find(b);
    parent[a] = b;
}

int main() {
    int n, A, B, ans = 0;
    cin >> n;

    for (int i = 1; i <= n; i++)
        parent[i] = i;

    for (int i = 1; i <= n; i++) {
        cin >> A >> B;
        merge(A, B);
    }

    for (int i = 1; i <= n; i++)
        if (i == find(i))
            ans++;

    cout << ans << endl;
    return 0;
}

精髓在于 find 函数，与构造子链

将 find 函数的代码拿出

while (x != parent[x]) {
    if (x < parent[x]) {
        // 路径压缩
        parent[x] = parent[parent[x]];
    }
    x = parent[x];
    counter++;
}

题目的要求是使 counter 尽可能的大，所以我们要尽可能的不进入 if 语句（尽可能的不路径压缩），即，让父节点尽可能地小于子节点，

我们可以构造类似的链状结构：

10 -> 9 -> 8 -> 7 -> 6 -> 5 -> 4 -> 3 -> 2 -> 1

此代码要想 find(7) 需要 counter + 6，因为他的每一个父节点都小于子节点，如此，每次都在 if 外面，使 counter ++，直到找到 1 为止

可以先构造一条链，再查找

题目样例代码解读：

此代码进入了 if 带路径压缩，该样例的图比较乱（类似1->3->5），此处不解读了，（画不好图，，，）

附上调试代码：根据调试的代码结果判断就行，咱重点不在这个（他这个样例写的太烂了，还进入 if ……，麻烦，，，）

#include <iostream>
using namespace std;
const int MAXN = 1e5+10;
int parent[MAXN];
long long counter = 0;

int find(int x) {
	int res = 0;
    while (x != parent[x]) {
        if (x < parent[x]) {
        	cout << "x1:" << x << " " << parent[x] <<  endl;
            // Merge-by-rank and Path-compression
            parent[x] = parent[parent[x]];
        }
        cout << "x2:" << x  << " " << parent[x]<< endl;
        x = parent[x];
        counter++, res++;
    }
    cout << res << endl;

    return x;
}

void merge(int a, int b) {
    a = find(a);
    b = find(b);
    //cout << "a:" << a << endl;
    //cout << "b:" << b << endl;
    parent[a] = b;
}

int main() {
    int n, A, B, ans = 0;
    cin >> n;

    for (int i = 1; i <= n; i++)
        parent[i] = i;

    for (int i = 1; i <= n; i++) {
        cin >> A >> B;
        merge(A, B);
    }

	cout << " ------------------ " << endl;

    for (int i = 1; i <= n; i++)
        if (i == find(i))
            ans++;

    cout << counter << endl;
}

自测代码解读：

不进入 if ，即，使 counter 最大化（最优解）

输入题目代码(以 n = 10 例子）

朴素版输入代码：

解读：

// 构造链
// 将 a -> b
// b -> c
10 9 // 10 -> 9
9 8 // 10 -> 9 -> 8
8 7 // 10 -> 9 -> 8 -> 7
7 6 // 10 -> 9 -> 8 -> 7 -> 6
6 5
5 4
4 3
3 2
2 1

// 截至至此，构造链的结果
// 10 -> 9 -> 8 -> 7 -> 6 -> 5 -> 4 -> 3 -> 2 -> 1

// 此插入无效，当成查找
1 10

在构造链时，counter = 0，每一个点都是父节点

在最后一步查找的时候在，find(1) 时，counter = 0；find(10) 时，counter + 9

最后在 for 循环计算 ans 时，find(1) ：counter + 0, find(2) = counter + 1, find(3) = counter + 2，…… find(10) = counter + 9

最终 counter 为（0 + 1 + 2 + 3 ……+ 9 ) + 9 = 54

样例输入代码进化版

// 构造链
// 将 a -> b
10 9 
9 8 
8 7 
7 6 
6 5
5 4
4 3
3 2
2 1

// 构造结果
// 10 -> 9 -> 8 -> 7 -> 6 -> 5 -> 4 -> 3 -> 2 -> 1

// 查找
10 10

将查找换为 10 10，主函数 for 循环得到的 counter 不变，只在最后一步插入时将 find(1) 改为 find(10) 总结果应该比上一次结果多 9 ，（find(1) ：counter + 0，find(10) ：counter + 0）counter = 54 + 9 = 63

超进化版

// 构造链
// 将 a -> b
10 9 // counter + 0
10 8 // counter + 1
10 7 // counter + 2
10 6 // counter + 3
10 5 // counter + 4
10 4 // counter + 5
10 3 // counter + 6
10 2 // counter + 7
10 1 // counter + 8

// 构造结果
// 10 -> 9 -> 8 -> 7 -> 6 -> 5 -> 4 -> 3 -> 2 -> 1

// 查找
10 10

边插入，边计算 counter

插入时 counter + 0 + 1 + 2 + …… + 8 即，counter + 36

其余和进化版一致

如此的到的 counter 比 普通版样例 多了 9 + 36

比进化版多了 36 个为恐怖的 99，思路完成

分析可行性：

，counter 一定越大越好，

题目： hack 到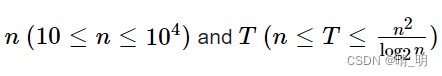，即 n^2 / log2(n)

朴素版的counter数量

res = (1+……n-1）+ n-1

res = n*n/2 + (n-1)-n/2

类似上述分析也成立

如此程度，我们 hack 到 res 连朴素版的都能过，超进化版还怕什么？？？，但学算法不能只停驻与AC，应该精益求精，接下来看进化版本的counter

进化版本的呢？

res = (n-1)*2 + (1+……+n-1)

res = (n-1)*2 + n*(n-1)/2

res = n*n/2 + (n-1)*2 - n/2

可知当 n > 10 时，log2(10) = 3.32

(n-1)*2 - n/2 > 0

n*n/2 > n*n/log2(10)

所以，成立

超进化版本的 res 可求为

res = ( 1+ ……+n-2) + (n-1) + (n-1) + (1+……n-1)

res = (1+……n-1) * 2 + (n-1)

res = (1+n-1)*(n-1) + (n-1)

res = n *（n - 1） + (n - 1)

res = n*(n-1) + n - 1

res = n*n - 1

因为 n > 10，log2(n) >= 3

res = n*n-1 >> n*n/log2(n)，（远大于）

所以超进化版本的一定成立

如此程度，我们 hack 到 res 连朴素版的都能过，超进化版还怕什么？？？

直接最优解（超进化版本）的代码：

超进化版本代码奉上：

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;

const int N = 310, mod = 1000003;

int n, m;

int main()
{
    scanf("%d %d", &n, &m);

    //printf("%d %d\n", n, 1);
    for(int i=n-1;i>=1;i--)
		cout<<n<<" "<<i<<"\n";
	cout<<n<<" "<<n;

    return 0;
}

确实都能AC，🤣

F. Function

方程拿过来，方便一点

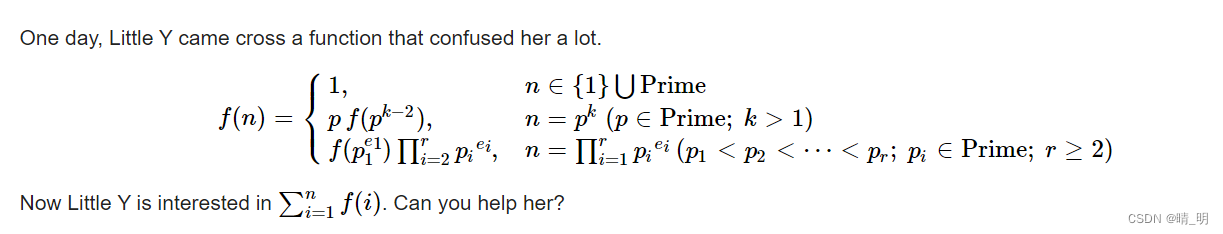
解释方程：

情况（1）：n 为质数，f(n) = 1

情况（2）：合数 n 可分解为唯一质数 p ，且质数的数量大于 1 ，f(n) = p^(k+1)

情况（3）：合数 n 可分解为很多质数的积（算术基本定理），分解完全后的其中最小的质数 p 的 e1 次方，拿去做情况（1）或情况（2）；

思路：

考虑到最小的质数，我么应该想到线性筛，

void get_primes(int n)
{
	for(int i = 2; i <= n; i ++ )
	{
		if(!st[i]) primes[cnt++] = i;
		for(int j = 0; primes[j] <= n/i; j ++ )
		{
			st[primes[j] * i] = true;
			if(i % primes[j] == 0) break; 
		 } 
	}
}

线性筛的筛掉合数有两种情况，

(1). 当 i % primes[j] == 0 时，primes[j] 为 i 的最小质因子，同时也是要筛的数 i*primes[j] 的最小质因子，此时将 i * primes[j] 中的 primes[j] 分解完全, 乘以分解后的 i * primes[j] 得到 f[ i * primes[j] ]

(2)，当 i % primes[j] != 0 时，primes[j] 不是 i 的质因子，primes[j] 为 i * primes[j] 的最小质因子，此时，因为 i 中没有 primes[j] 所以，primes[j] 的 k 为 1，f[ primes[j] ^ k] = 1,还剩下 i ，res *= i;

注：res 初始化为 1，f[1] = 1，且 1 没法筛出去，，，

代码如下：

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;

const int N = 1e7+10;

int n;
int cnt;
int primes[N];
bool st[N];
LL res = 1;

LL qmi(int a, int k)
{
    LL ans = 1;
    while(k)
    {
        if(k & 1) ans = (LL)ans*a;
        k >>= 1;
        a = (LL)a*a;
    }
    return ans;
}

void get_primes()
{
    for(int i = 2; i <= n; i ++ )
    {
        if(!st[i])
        {
            primes[cnt ++] = i;
            res ++;
        }
        for(int j = 0; primes[j] <= n/i; j ++ )
        {
            st[i * primes[j]] = true;

            // primes[j] 是 i 的最小质因子，也是 i * priems[j] 的最小质因子
            if(i % primes[j] == 0)
            {
                int s = 1;
                int t = i;
                while(t % primes[j] == 0) t /= primes[j], s ++;
                res += (LL)qmi(primes[j], s/2) * t;
                break;
            }
            // primes[j] 不是 i 的最小质因子，但primes[j] 是 i * primes[j] 的最小质因子，
            // 所以推出 primes[j] 为 i*primes[j] 的最小的唯一质因子，f(primes[j]的个数 k==1 ) = 1;
            res += i; // 等价于 res += f(k)*i;
        }
    }
}

int main()
{
    scanf("%d", &n);

    get_primes();

    cout << res << endl;

    return 0;
}

J. JOJO's Factory

思路：

(1)由题目数据范围可知，M < 2*N - 3，远小于所有的边数 N*N，所以不可能所有的A机器同时存在只能连一个B机器的情况（需要N*(N-1)条边）。

(2) 一个机器完全报废为需要N，两个相同种类的机器报废为2*N，最多只能出现一个A机器报废（都不能连）或一个B机器报废，或同时报废A，B一个的情况，。

(3) 因为不存在只能连一个的情况，没报废的机器A可以与没报废的机器B任意连，可以连成一对的数量为 min(A,B)(没报废的最小值）

代码实现：

朴素版：map此机器不能连的的个数，若等于 n 则报废，对应的种类的机器数量 - 1，最后求min即可

代码如下：

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;

const int N = 310, mod = 1000003;

int n, m;
map<int, int> mpa;
map<int, int> mpb;

int main()
{
    scanf("%d %d", &n, &m);

    int a, b;
    int t = 0;
    for(int i = 1; i <= m; i ++ )
    {
        scanf("%d %d", &a, &b);
        mpa[a] ++;
        mpb[b] ++;
        if(mpa[a] >= n) t = 1;
        if(mpb[b] >= n) t = 1;
    }

    printf("%d\n", n-t);

    return 0;
}

貌似时间有点紧，，，差4毫秒，，

用unordered_map试一下，1450ms，，显著提高了500ms

更优化版：

思路：我们知道A，B 中最多只能有一个报废，所以，标记报废数 t ，若存在报废的了(t == 1)，其他的就不用存入 unordered_map，

又优化了点

优化代码如下：（unordered_map）实现

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;

const int N = 310, mod = 1000003;

int n, m;
unordered_map<int, int> mpa;
unordered_map<int, int> mpb;

int main()
{
    scanf("%d %d", &n, &m);

    int a, b;
    int t = 0;
    for(int i = 1; i <= m; i ++ )
    {
        scanf("%d %d", &a, &b);

        if(t == 1) continue;

        mpa[a] ++;
        mpb[b] ++;
        if(mpa[a] >= n) t = 1;
        if(mpb[b] >= n) t = 1;
    }

    printf("%d\n", n-t);

    return 0;
}

但虽然unordered_map插入删除的操作时间复杂度接近O(1)，但也是不稳定的，冲突过多会变成O(log(n))，

再次观察数据范围，N < 1e5，这个长度完全可以用数组实现，插入删除绝对的O(1)，

再更优化代码：（数组实现）

时间空间复杂度都有显著降低，至此优化完成，

最终思路为：标记唯一报废的机器，存在则 t == 1，之后continue，输出 n - 1；否则正常存入，输出 n

最终代码：

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;

const int N = 1e6+10, mod = 1000003;

int n, m;
int mpa[N];
int mpb[N];

int main()
{
    scanf("%d %d", &n, &m);

    int a, b;
    int t = 0;
    for(int i = 1; i <= m; i ++ )
    {
        scanf("%d %d", &a, &b);

        if(t == 1) continue;

        mpa[a] ++;
        mpb[b] ++;
        if(mpa[a] >= n) t = 1;
        if(mpb[b] >= n) t = 1;
    }

    printf("%d\n", n-t);

    return 0;
}

K. Keep Eating

思路：

全部合并，一点一点吃，每次吃 1 块，重量到 k 时，只吃的小一部分，剩余 k/2上取整数

（签到题）代码如下：

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;

const int N = 2e5+10;

int n, m;
LL sum = 0;

int main()
{
    scanf("%d %d", &n, &m);

    int x;
    for(int i = 1; i <= n; i ++ )
        scanf("%d", &x), sum += x;

    if(sum >= m) printf("%lld\n", sum - (m+1)/2);
    else puts("0");

    return 0;
}