目录
2.3.3. 第三种情况:所删除的节点有两个非空节点 && 找右子树的最左节点
1. 二叉搜索树的概念及结构
学习二叉搜索树的一些原因:
- map 和 set 特性需要先铺垫二叉搜索树,而二叉搜索树也是一种树形结构;
- 二叉搜索树的特性了解,有助于更好的理解 map 和 set 的特性。
1.1. 二叉搜索树的概念
二叉搜索树(Binary Search Tree,简称BST) 又名为二叉排序树或者是二叉查找树。它可能是一棵空树,或者是满足下面性质的二叉树:
- 如果它的左子树不为空,那么左子树上的所有节点的值都要小于根节点的值;
- 如果它的右子树不为空,那么右子树上的所有节点的值都要大于根节点的值;
- 它的左右子树也是一颗二叉搜索树。
对于一颗二叉搜索树,它的中序遍历可以得到有序的数据;
需要注意的是,二叉搜索树要求每个节点的值都唯一,如果存在重复的值,可以在节点中添加计数器来解决。
1.2. 二叉搜索树的结构样例
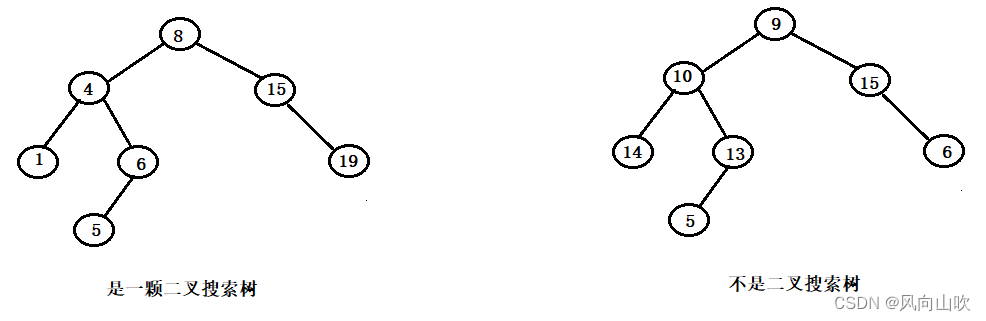
一棵树是否是一颗二叉搜索树,必须要符合二叉搜索树的性质。
为了更好地理解二叉搜索树,我们需要其进行模拟实现:
2. 二叉搜索树的实现
2.1. insert 的非递归实现
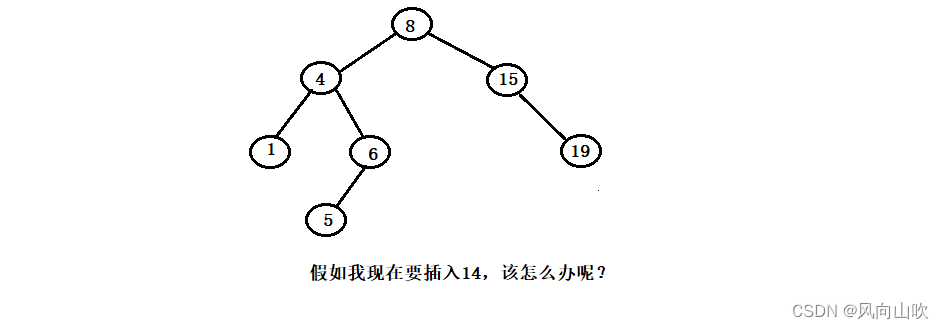
对于二叉搜索树的插入,我们需要满足插入后的二叉树仍旧是一颗二叉搜索树,也就是说,插入的元素必须要被插入到特定的位置,以维持二叉搜索树的结构。如上图所示,如果要插入14,那么它的位置是确定的,如下图所示:
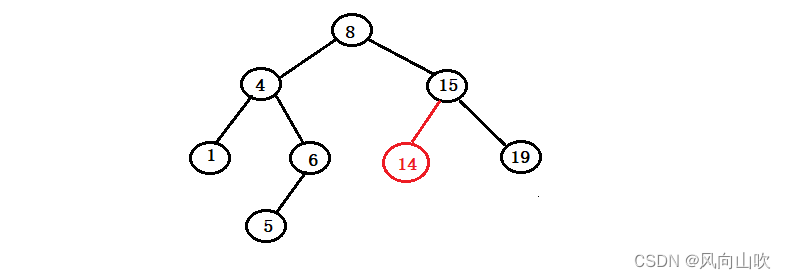
因此 insert 的具体实现我们可以分解为两个过程:
- 第一步:找到要插入元素的位置;
- 第二步:插入元素,完成连接关系。
注意:在这里实现的二叉搜索树的每个值具有唯一性,相同值不插入。
bool insert(const T& key)
{
// 1. 如果是空树,直接对_root赋值即可,插入成功并返回true
if (_root == nullptr)
{
_root = new Node(key);
return true;
}
else
{
// step 1: 先找目标位置
Node* cur = _root;
// 为了更好的连接新节点, 因此记录父节点
Node* parent = nullptr;
while (cur)
{
// 如果当前节点的Key大于目标Key
// 当前节点应该向左子树走
if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
// 如果当前节点的Key小于目标Key
// 当前节点应该向右子树走
else if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else
{
// 找到了相同的 key, 在这里不插入
return false;
}
}
// cur 走到了空, 即 cur 就是合适的位置
cur = new Node(key);
// 我们需要判断cur是parent的左节点还是右节点
// 如果key小于parent的key,那么插入左节点
if (key < parent->_key)
parent->_left = cur;
// 反之连接到右节点
else
parent->_right = cur;
return true;
}
}2.2. find 的非递归实现
find 就很简单了,没什么要说的,根据传递的 key 进行判断,大于当前节点,那么当前节点向左走,反之向右走,如果相等,返回true,循环结束,则说明没有这个key,实现如下:
bool find(const T& key)
{
// 1. 从根节点开始
Node* cur = _root;
while (cur)
{
// 2. 如果当前关键字大于目标关键字,那么向左子树走
if (cur->_key > key)
cur = cur->_left;
// 3. 如果小于目标关键字,那么向右子树走
else if (cur->_key < key)
cur = cur->_right;
// 4. 相等,就返回true
else
return true;
}
// 5. 循环结束,说明没找到, 返回false
return false;
}2.3. erase 的非递归实现
对于搜索二叉树来说,真正有一些难度的是删除,对于删除我们可以分解为不同的情况,根据对应的情况,以特点方式解决。
在这里我们分为三种情况:
- 所删除的节点的左孩子为空:托孤法删除;
- 所删除的节点的右孩子为空:托孤法删除;
- 所删除的节点的有两个非空孩子:替代法删除。
注意:对于叶子结点的处理可以归为第一类情况或者第二类情况。
为了可以更好的理解上面的三种情况,我们用图来说话:
2.3.1. 第一种情况:所删除的节点的左孩子为空
如图所示:假如现在我们要删除的节点是15节点,可以发现它的左孩子为空,那么如何删除呢?
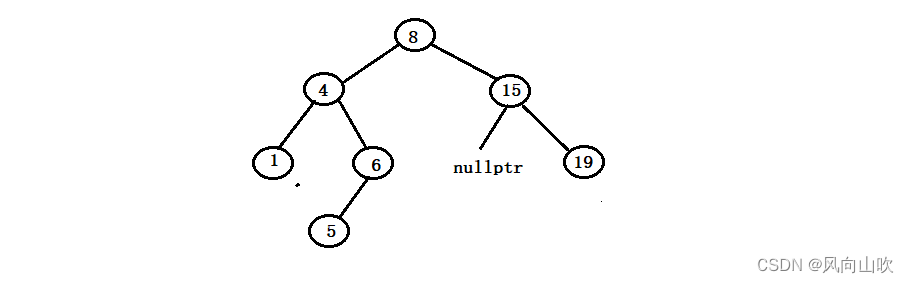
我们的方法是托孤法删除,什么叫托孤法删除呢?
就是将15的非空孩子(在这里就是19)交给它的父亲节点(在这里就是8),如图所示:
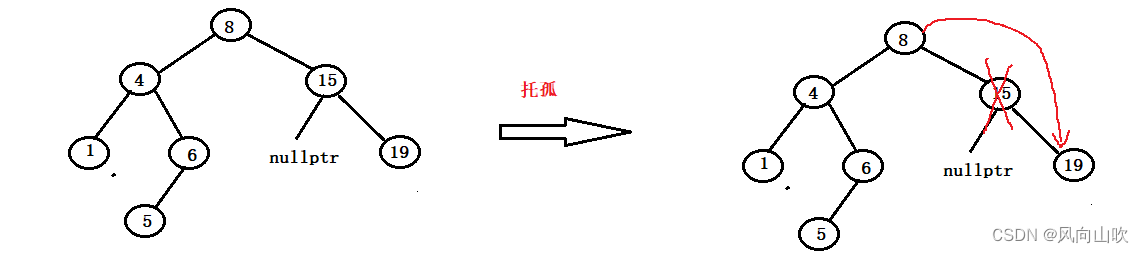
注意:在这里一定是父亲节点的右孩子指向被删除的节点的非空孩子吗?
答案是,不一定,我们需要根据被删除节点和父亲节点的关系判断:
- 如果被删除节点是父亲节点的右孩子,那么在这里就是父亲节点的右孩子指向被删除节点的非空节点;
- 如果被删除节点是父亲节点的左孩子,那么在这里就是父亲节点的左孩子指向被删除节点的非空节点。
代码如下:
2.3.1.1. 错误的代码
// 第一种情况: 所删除的节点的左孩子为空
if (del->_left == nullptr)
{
if (del_parent->_left == del)
{
del_parent->_left = del->_right;
}
else
{
del_parent->_right = del->_right;
}
delete del;
del = nullptr;
}可能我们认为这段代码没问题,但是如果是下面这种情况呢?
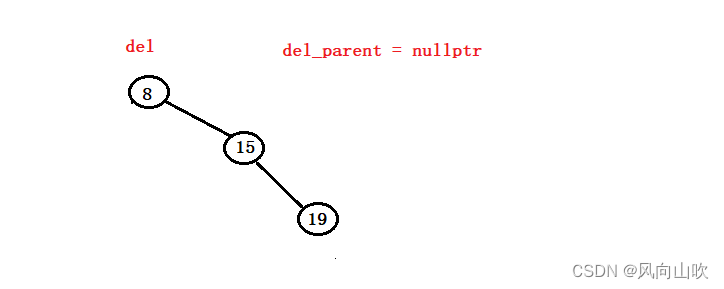
如果我此时要删除8,而8是这棵树的根节点,它是没有父节点的,那么此时上面的代码就会崩溃;
为了解决这个隐患,我们的方案就是,如果被删除节点是根,且它的左子树为空树,那么我们更新根节点即可,在这里就是让15做根节点。
2.3.1.2. 正确的代码
//第一种情况:所删除的节点的左孩子为空
if (del->_left == nullptr)
{
// 如果被删除节点是根,那么更新根即可
if (del == _root)
{
Node* newroot = del->_right;
delete _root;
_root = newroot;
}
// 被删除节点是非根节点
else
{
if (del_parent->_left == del)
{
del_parent->_left = del->_right;
}
else
{
del_parent->_right = del->_right;
}
delete del;
}
}2.3.2. 第二种情况:所删除的节点的右孩子为空
如图所示:假如现在我们要删除的节点是6节点,可以发现它的右孩子为空,那么如何删除呢?
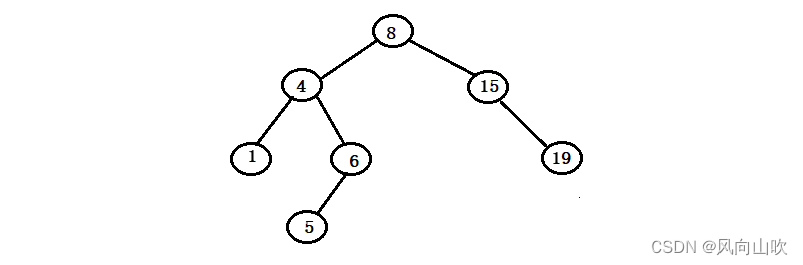
方案依旧是托孤法删除,在这里就是将6(被删除节点)的5(非空孩子节点)交给4(父亲节点) ,如下:
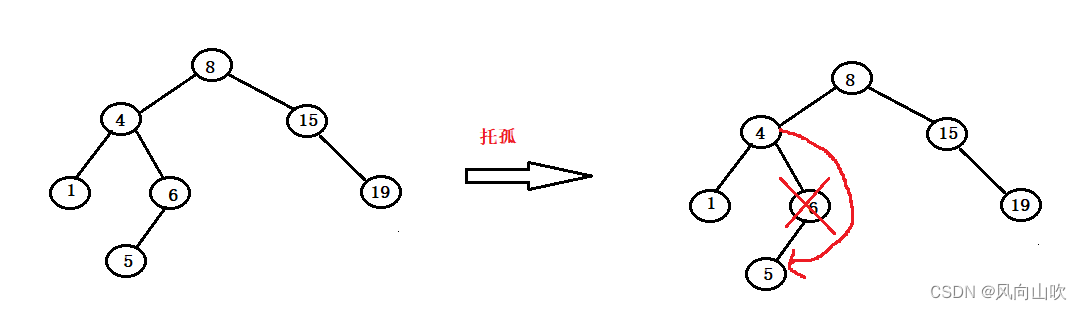
处理细节,和第一种情况大同小异。
需要注意的就是:最后父亲节点连接非空孩子节点的时候,要根据被删除节点是父亲节点的左孩子还是右孩子来判断。
第二种情况和第一种情况大同小异,也需要对根节点进行特殊处理:
代码如下:
2.3.2.1. 正确的代码
//第二种情况:所删除的节点的右孩子为空
else if (del->_right == nullptr)
{
// 当被删除节点为根节点
if (del == _root)
{
Node* newroot = del->_left;
delete del;
_root = newroot;
}
//当被删除节点为非根节点
else
{
if (del_parent->_left == del)
{
del_parent->_left = del->_left;
}
else
{
del_parent->_right = del->_left;
}
delete del;
del = nullptr;
}
}2.3.3. 第三种情况:所删除的节点有两个非空节点 && 找右子树的最左节点
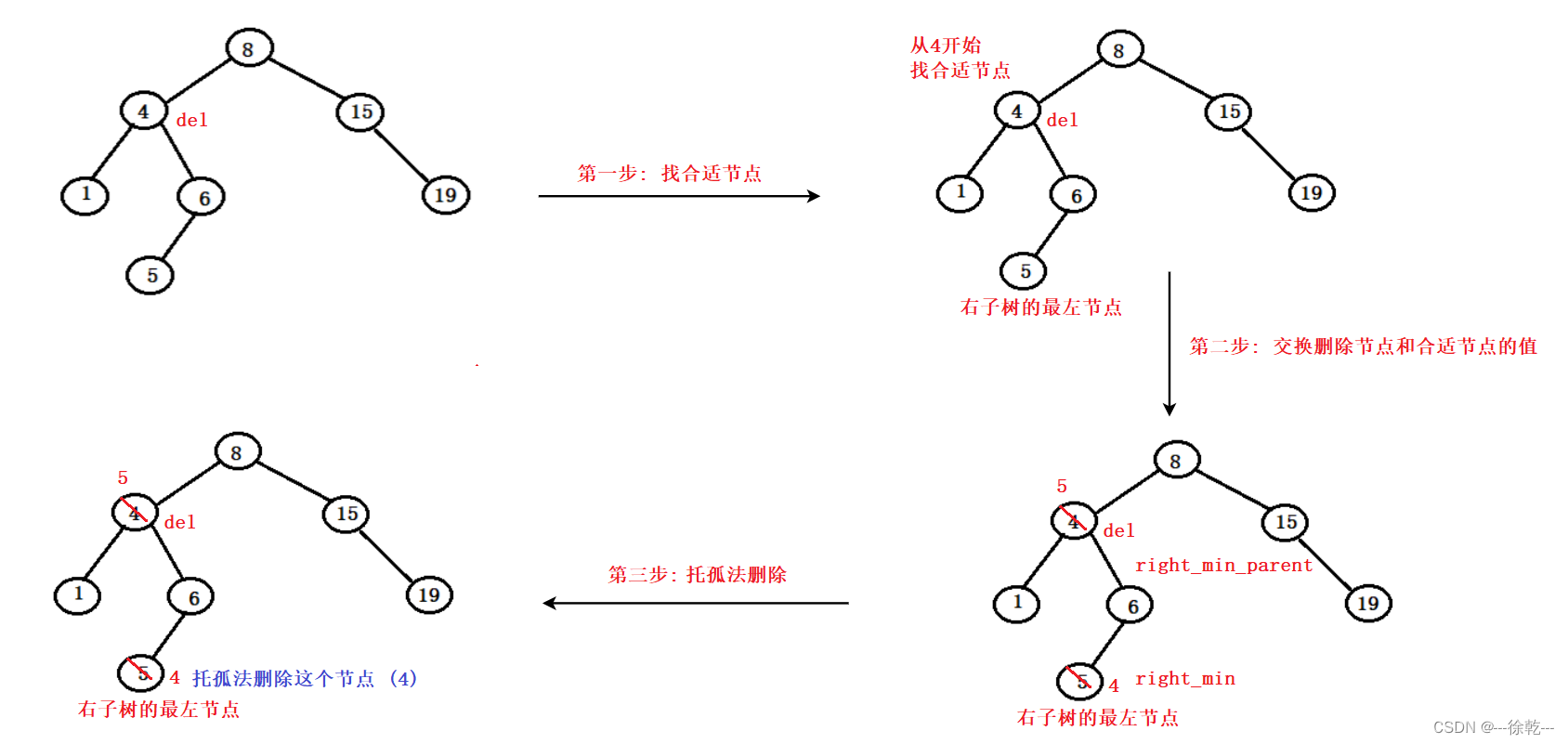
较为复杂的就是第三种情况了,由于被删除的节点有两个孩子,因此无法托孤,因为父亲节点至多只能管理两个孩子,所以我们又提出了新的解决方案:替代法删除
如图所示:
假如现在我们要删除4所在的节点,可以发现,4所在的节点有两个孩子,因此无法托孤,那么我们需要采用替代法删除,替代法删除就是在左子树或者右子树找一个"合适节点",将4所在的节点的key进行覆盖,将删除4所在的节点转化为删除我们找的这个"合适节点"。
而这个"合适节点"通常只有两个:
- 其一:以被删除的节点所在的二叉树开始,左子树的最大节点,即左子树的最右(大)节点;
- 其二:以被删除的节点所在的二叉树开始,右子树的最小节点,即右子树的最左(小)节点。
而我们在这里就找右子树的最左(小)节点,注意,要从被删除的节点开始,在这里就是5;
当找到这个 "合适节点" 后,交换它与要删除节点的 Key;
此时就将删除目标节点转换为删除这个 "合适节点" 了;
因为此时这个 "合适节点" 只会有两种情况:
- 第一种:它没有孩子,即左右子树为空;
- 第二种:它只有一个孩子,且只可能是右孩子,因为这个 "合适节点" 是右子树的最左节点;
如果是第一种,即没有孩子,我们也可以将其归类为第二种情况,即右孩子不为空 && 左孩子为空,因此,可以用统一的方式处理,即托孤法删除 (所删除的节点的左孩子为空)。
故我们的大致步骤如下:
- 找合适节点;
- 交换合适节点和删除节点的 Key;
- 托孤发删除合适节点。
如图所示:
2.3.3.1. 有错误的代码
// 第三种情况:所删除的节点有两个非空节点
else
{
// 从被删除结点开始, 找右子树的最小(左)节点
Node* right_min = del->_right;
// 并记录这个节点的父亲节点
// 有可能这里我们会习惯的从nullptr开始,但是对于某些特殊情况会崩溃
Node* right_min_parent = nullptr;
while (right_min->_left)
{
right_min_parent = right_min;
right_min = right_min->_left;
}
// 交换这个节点和要删除节点的 key
std::swap(del->_key, right_min->_key);
// 将删除 del 转化为删除 right_min (托孤法删除)
if (right_min_parent->_left == right_min)
right_min_parent->_left = right_min->_right;
else
right_min_parent->_right = right_min->_right;
delete right_min;
right_min = nullptr;
}如果我们将"合适节点"的父节点初始值设为nullptr,那么在下面的场景会发生崩溃:
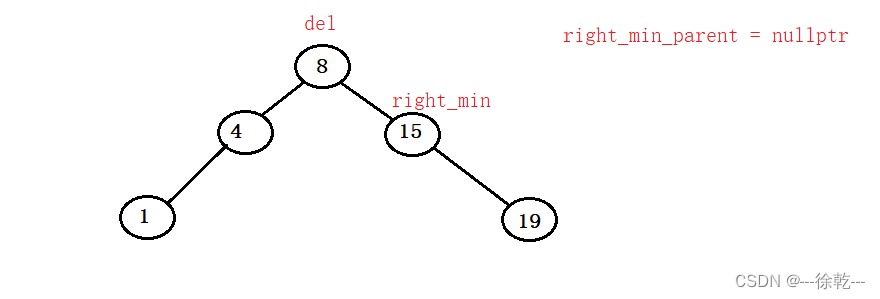
由于此时,这个 "合适节点" 正好是 del->_right,不会进入循环,那么 right_min_parent 就是空,那么后面的操作就会对空指针进行解引用,非法操作,进程崩溃。
因此这里的 right_min_parent 的初始值可以从 del 开始,不可以将初始值设为空。
同时,我们发现,最后进行托孤法删除时,我们也进行了判断,这样的原因是因为这个"合适节点"既可能是父节点的左孩子,也可能是父节点的右孩子,因此必须判断。
2.3.3.2. 正确的代码
// 第三种情况:所删除的节点有两个非空节点
else
{
// 从被删除结点开始, 找右子树的最小(左)节点
Node* right_min = del->_right;
// 并记录这个节点的父亲节点, 让其从del开始
Node* right_min_parent = del;
while (right_min->_left)
{
right_min_parent = right_min;
right_min = right_min->_left;
}
// 交换这个节点和要删除节点的 key
std::swap(del->_key, right_min->_key);
// 将删除 del 转化为删除 right_min (托孤法删除)
if (right_min_parent->_left == right_min)
right_min_parent->_left = right_min->_right;
else
right_min_parent->_right = right_min->_right;
delete right_min;
right_min = nullptr;
}以此类推,我们也可以找左子树的最大(右)节点,代码如下:
else
{
// 从被删除节点开始, 找左子树的最大(右)节点
Node* left_max = del->_left;
// 并记录这个节点的父亲节点, 让其从del开始
Node* left_max_parent = del;
while (left_max->_right)
{
left_max_parent = left_max;
left_max = left_max->_right;
}
// 交换这个节点和要删除节点的 key
std::swap(del->_key, left_max->_key);
// 将删除 del 转化为删除 left_max (托孤法删除)
if (left_max_parent->_left == left_max)
left_max_parent->_left = left_max->_left;
else
left_max_parent->_right = left_max->_left;
delete left_max;
left_max = nullptr;
}最后,我们将第三种情况汇总,第一种是找右子树的最左节点,第二种是找左子树的最右节点,如下:
else
{
// 从被删除节点开始, 找右子树的最小(左)节点 || 找左子树的最大(右)节点
if (del->_right)
_erase_right_min_node(del);
else
_erase_left_max_node(del);
}
void _erase_right_min_node(Node* del)
{
// 从被删除结点开始, 找右子树的最小(左)节点
Node* right_min = del->_right;
// 并记录这个节点的父亲节点, 让其从del开始
Node* right_min_parent = del;
while (right_min->_left)
{
right_min_parent = right_min;
right_min = right_min->_left;
}
// 交换这个节点和要删除节点的 key
std::swap(del->_key, right_min->_key);
// 将删除 del 转化为删除 right_min (托孤法删除)
if (right_min_parent->_left == right_min)
right_min_parent->_left = right_min->_right;
else
right_min_parent->_right = right_min->_right;
delete right_min;
right_min = nullptr;
}
void _erase_left_max_node(Node* del)
{
// 从被删除节点开始, 找左子树的最大(右)节点
Node* left_max = del->_left;
// 并记录这个节点的父亲节点, 让其从del开始
Node* left_max_parent = del;
while (left_max->_right)
{
left_max_parent = left_max;
left_max = left_max->_right;
}
// 交换这个节点和要删除节点的 key
std::swap(del->_key, left_max->_key);
// 将删除 del 转化为删除 left_max (托孤法删除)
if (left_max_parent->_left == left_max)
left_max_parent->_left = left_max->_left;
else
left_max_parent->_right = left_max->_left;
delete left_max;
left_max = nullptr;
}2.3.4. erase的完整实现如下
bool erase(const T& key)
{
// 先找要删除的节点
Node* del = _root;
Node* del_parent = nullptr;
while (del)
{
if (del->_key < key)
{
del_parent = del;
del = del->_right;
}
else if (del->_key > key)
{
del_parent = del;
del = del->_left;
}
else
{
// 锁定了要删除的节点
// 分三种情况:
// case 1: 左子树为空
if (del->_left == nullptr)
{
// 如果要删除的节点是根
if (del == _root)
{
Node* newroot = del->_right;
delete _root;
_root = newroot;
}
else
{
// 托孤法删除
if (del_parent->_left == del)
del_parent->_left = del->_right;
else
del_parent->_right = del->_right;
delete del;
del = nullptr;
}
}
// case 2: 右子树为空
else if (del->_right == nullptr)
{
if (_root == del)
{
Node* newroot = del->_left;
delete _root;
_root = newroot;
}
else
{
if (del_parent->_left == del)
del_parent->_left = del->_left;
else
del_parent->_right = del->_left;
delete del;
del = nullptr;
}
}
// case 3: 左右子树都不为空
else
{
// 从被删除节点开始, 找右子树的最小(左)节点 || 找左子树的最大(右)节点
if (del->_right)
_erase_right_min_node(del);
else
_erase_left_max_node(del);
}
return true;
}
}
return false;
}
void _erase_right_min_node(Node* del)
{
// 从被删除结点开始, 找右子树的最小(左)节点
Node* right_min = del->_right;
// 并记录这个节点的父亲节点, 让其从del开始
Node* right_min_parent = del;
while (right_min->_left)
{
right_min_parent = right_min;
right_min = right_min->_left;
}
// 交换这个节点和要删除节点的 key
std::swap(del->_key, right_min->_key);
// 将删除 del 转化为删除 right_min (托孤法删除)
if (right_min_parent->_left == right_min)
right_min_parent->_left = right_min->_right;
else
right_min_parent->_right = right_min->_right;
delete right_min;
right_min = nullptr;
}
void _erase_left_max_node(Node* del)
{
// 从被删除节点开始, 找左子树的最大(右)节点
Node* left_max = del->_left;
// 并记录这个节点的父亲节点, 让其从del开始
Node* left_max_parent = del;
while (left_max->_right)
{
left_max_parent = left_max;
left_max = left_max->_right;
}
// 交换这个节点和要删除节点的 key
std::swap(del->_key, left_max->_key);
// 将删除 del 转化为删除 left_max (托孤法删除)
if (left_max_parent->_left == left_max)
left_max_parent->_left = left_max->_left;
else
left_max_parent->_right = left_max->_left;
delete left_max;
left_max = nullptr;
}二叉树进阶 --- 上,至此结束。






















 427
427

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








