算法世界的两极对话：从正则表达到中位数寻找的思维盛宴-CSDN博客

亲爱的算法探险家们，欢迎来到今日的思维迷宫！在这个数字世界的深处，隐藏着两个看似截然不同却同样迷人的算法挑战：一个是如同语言学家般精巧的正则表达式匹配，另一个则是如统计学家般精准的中位数寻找。它们分别代表了模式匹配与数值计算两大算法领域的精华，犹如算法世界中的阴阳两极，既对立又统一。

今天，我们将一起解开这两个问题的神秘面纱，探索它们背后的算法思维和设计哲学。无需编写一行代码，我们将聚焦于思维过程和分析方法，体验算法设计的艺术与科学。准备好了吗？让我们开始这段奇妙的算法之旅！

第一幕：正则表达式匹配 - 模式识别的艺术

题目描述：
给你一个字符串 s 和一个字符规律 p，请你来实现一个支持 '.' 和 '*' 的正则表达式匹配。

'.' 匹配任意单个字符
'*' 匹配零个或多个前面的那一个元素
所谓匹配，是要涵盖整个字符串 s 的，而不是部分字符串。

问题深度解析

正则表达式匹配问题要求我们实现一个简化版的正则引擎，核心在于处理两个特殊字符：'.'和'*'。这不仅仅是一个简单的字符串匹配问题，更是一个涉及状态转移和回溯机制的复杂模式识别系统。

'.'字符相当于通配符，可以匹配任何单个字符，这引入了不确定性。而'*'字符更加复杂，它允许前面字符的零次或多次重复，这创造了多重可能性空间。这两种特殊字符的组合使得简单的线性匹配算法无法解决问题，必须采用更高级的算法策略。

算法思维剖析

动态规划：状态机的智慧

解决这个问题的关键在于采用动态规划(Dynamic Programming)方法。我们定义一个二维DP表，其中dp[i][j]表示字符串s的前i个字符能否与模式p的前j个字符匹配。

这种方法的精妙之处在于它将复杂问题分解为相互关联的子问题，每个子问题的解都基于更小子问题的解。这种自底向上的解决方案避免了重复计算，大大提高了效率。

状态转移方程的设计艺术

设计状态转移方程是这个算法的核心挑战，需要处理三种情况：

普通字符匹配：当p的当前字符是普通字母时，必须精确匹配
'.'通配符：可以匹配任何字符，相当于无条件匹配
'*'通配符：需要同时考虑匹配零次和匹配多次的情况

''字符的处理最为精妙：当遇到''时，我们有两种选择：

忽略前一个字符和'*'（匹配零次）
如果前一个字符匹配，则保留'*'以便继续匹配（匹配多次）

这种决策分支的处理体现了动态规划的优势：能够系统性地探索所有可能性而不陷入递归的深渊。

复杂度分析
该算法的时间复杂度和空间复杂度均为O(m×n)，其中m和n分别是字符串s和模式p的长度。这在给定的约束条件下是完全可行的。
示例 1：

输入：s = "aa", p = "a"
输出：false
解释："a" 无法匹配 "aa" 整个字符串。
示例 2:

输入：s = "aa", p = "a*"
输出：true
解释：因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此，字符串 "aa" 可被视为 'a' 重复了一次。
示例 3：

输入：s = "ab", p = ".*"
输出：true
解释：".*" 表示可匹配零个或多个（'*'）任意字符（'.'）。

题目程序：

#include <stdio.h>
#include <stdbool.h>
#include <string.h>
#include <stdlib.h>

bool isMatch(char* s, char* p) {
    int s_len = strlen(s);
    int p_len = strlen(p);
    
    // 创建dp表，大小为 (s_len+1) x (p_len+1)
    bool** dp = (bool**)malloc((s_len + 1) * sizeof(bool*));
    for (int i = 0; i <= s_len; i++) {
        dp[i] = (bool*)malloc((p_len + 1) * sizeof(bool));
        for (int j = 0; j <= p_len; j++) {
            dp[i][j] = false;
        }
    }
    
    // 空字符串和空模式匹配
    dp[0][0] = true;
    
    // 处理模式中开头可能有"a*"之类可以匹配0次的情况
    for (int j = 1; j <= p_len; j++) {
        if (p[j - 1] == '*') {
            dp[0][j] = dp[0][j - 2];
        }
    }
    
    for (int i = 1; i <= s_len; i++) {
        for (int j = 1; j <= p_len; j++) {
            if (p[j - 1] == '*') {
                // 匹配0次：忽略前一个字符和'*'
                if (dp[i][j - 2]) {
                    dp[i][j] = true;
                } else {
                    // 匹配多次：检查当前字符是否匹配前一个字符，并且之前的部分也匹配
                    if (s[i - 1] == p[j - 2] || p[j - 2] == '.') {
                        dp[i][j] = dp[i - 1][j];
                    }
                }
            } else if (p[j - 1] == '.' || s[i - 1] == p[j - 1]) {
                // 当前字符匹配，取决于之前的部分
                dp[i][j] = dp[i - 1][j - 1];
            }
        }
    }
    
    bool result = dp[s_len][p_len];
    
    // 释放dp表内存
    for (int i = 0; i <= s_len; i++) {
        free(dp[i]);
    }
    free(dp);
    
    return result;
}

int main() {
    // 示例测试
    printf("Example 1: %s\n", isMatch("aa", "a") ? "true" : "false"); // 输出false
    printf("Example 2: %s\n", isMatch("aa", "a*") ? "true" : "false"); // 输出true
    printf("Example 3: %s\n", isMatch("ab", ".*") ? "true" : "false"); // 输出true
    
    return 0;
}

输出结果：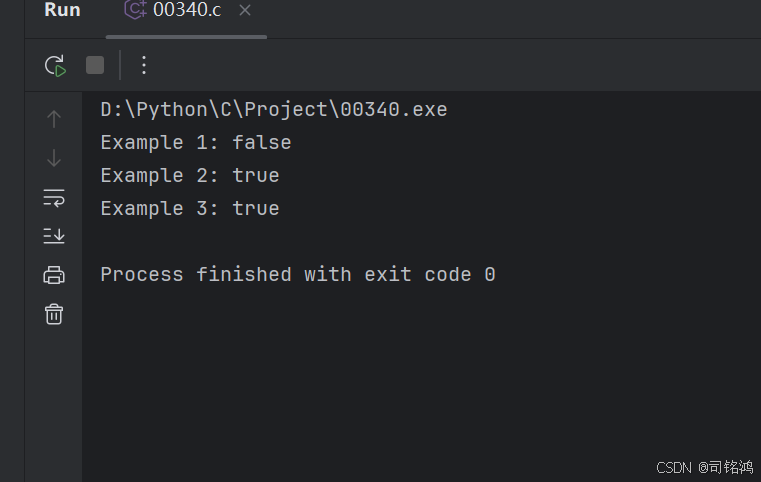

第二幕：寻找两个正序数组的中位数 - 数据集合的平衡之术

题目描述：
给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的中位数。

算法的时间复杂度应该为 O(log (m+n)) 。

问题本质探微

中位数问题要求我们在两个已排序的数组中找到合并后的中位数，关键在于达到O(log(m+n))的时间复杂度。这意味着我们不能简单地合并数组（那需要O(m+n)时间），而需要更巧妙的方法。

中位数代表着数据集的"中心点"，在统计中具有重要意义。它不像平均值那样容易受极端值影响，能够更好地反映数据的集中趋势。这个问题本质上是在寻找一种高效的分治策略，避免不必要的计算。

算法思维解密

二分查找的升华应用

解决方案基于二分查找(Binary Search)的扩展，但比传统二分查找更加精妙。我们不是在单个数组中查找，而是在两个数组的虚拟合并结构中寻找第k小的元素。

算法的核心思想是：每次比较两个数组中第k/2位置的元素，然后排除不可能包含中位数的那部分数组。这种逐步减半的策略确保了对数级别的时间复杂度。

分区概念的巧妙运用

更优雅的解决方案基于分区概念：我们在较短的数组上进行二分查找，寻找一个分区点，使得：

左半部分包含的元素数量等于右半部分（或相差1）
左半部分的所有元素小于等于右半部分的所有元素

这种方法的美丽之处在于它模拟了合并过程而不实际合并数组，通过智能比较和排除来缩小搜索空间。

边界条件的精密处理

这个算法的实现需要极其精密的边界条件处理，包括：

处理空数组的情况
确保分区点不会越界
正确处理奇偶长度的情况

这些细节处理体现了算法设计的严谨性和完备性要求。

示例 1：

输入：nums1 = [1,3], nums2 = [2]
输出：2.00000
解释：合并数组 = [1,2,3] ，中位数 2
示例 2：

输入：nums1 = [1,2], nums2 = [3,4]
输出：2.50000
解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5

题目程序:

#include <stdio.h>
#include <stdlib.h>

double findKth(int* nums1, int nums1Size, int* nums2, int nums2Size, int k) {
    int index1 = 0;
    int index2 = 0;
    
    while (1) {
        if (index1 == nums1Size) {
            return nums2[index2 + k - 1];
        }
        if (index2 == nums2Size) {
            return nums1[index1 + k - 1];
        }
        if (k == 1) {
            return nums1[index1] < nums2[index2] ? nums1[index1] : nums2[index2];
        }
        
        int half = k / 2;
        int newIndex1 = index1 + half - 1 < nums1Size ? index1 + half - 1 : nums1Size - 1;
        int newIndex2 = index2 + half - 1 < nums2Size ? index2 + half - 1 : nums2Size - 1;
        
        if (nums1[newIndex1] <= nums2[newIndex2]) {
            k -= (newIndex1 - index1 + 1);
            index1 = newIndex1 + 1;
        } else {
            k -= (newIndex2 - index2 + 1);
            index2 = newIndex2 + 1;
        }
    }
}

double findMedianSortedArrays(int* nums1, int nums1Size, int* nums2, int nums2Size) {
    int totalLength = nums1Size + nums2Size;
    if (totalLength % 2 == 1) {
        return findKth(nums1, nums1Size, nums2, nums2Size, (totalLength + 1) / 2);
    } else {
        double left = findKth(nums1, nums1Size, nums2, nums2Size, totalLength / 2);
        double right = findKth(nums1, nums1Size, nums2, nums2Size, totalLength / 2 + 1);
        return (left + right) / 2.0;
    }
}

int main() {
    int nums1[] = {1, 3};
    int nums2[] = {2};
    int size1 = sizeof(nums1) / sizeof(nums1[0]);
    int size2 = sizeof(nums2) / sizeof(nums2[0]);
    printf("Example 1: %.5f\n", findMedianSortedArrays(nums1, size1, nums2, size2)); // 输出 2.00000

    int nums3[] = {1, 2};
    int nums4[] = {3, 4};
    int size3 = sizeof(nums3) / sizeof(nums3[0]);
    int size4 = sizeof(nums4) / sizeof(nums4[0]);
    printf("Example 2: %.5f\n", findMedianSortedArrays(nums3, size3, nums4, size4)); // 输出 2.50000

    return 0;
}

输出结果: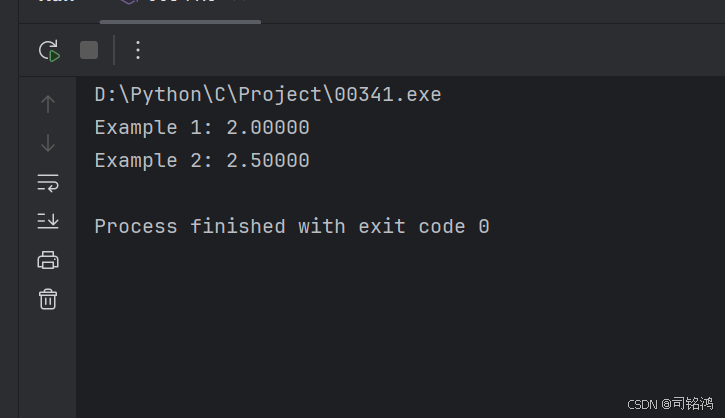

第三幕：双雄对比 - 思维模式的差异与统一

为了更直观地理解这两个算法的异同，让我们通过以下对比图表进行分析：

对比维度	正则表达式匹配	中位数寻找
问题类型	模式匹配、字符串处理	数值计算、统计分析
核心算法	动态规划	二分查找的变体
时间复杂度	O(m×n)	O(log(m+n))
空间复杂度	O(m×n)	O(1)
主要挑战	处理'*'的多种可能性	不合并数组找到中位数
思维模式	状态转移、回溯思维	分治策略、排除法
基础数据结构	二维DP表	数组索引、指针
关键操作	字符比较、状态更新	元素比较、分区计算
最优子结构	是	是
重叠子问题	是	否