数值分析实验（二）迭代法的应用

目录

实验名称：数值分析实验(二)迭代法的应用

实验题目：

实验原理:

         (1)高斯消去法

(2)Jacobi迭代法

(3)G-S迭代法

(4)SOR迭代法

实验数据记录及处理：

实验内容及步骤：

(1)高斯消元法:

(2)Jacobi迭代法：

(3)G-S迭代法

(4)SOR迭代法:

---

实验名称：数值分析实验(二)迭代法的应用

实验题目：

  考虑方程组=b的解,其中系数矩阵H为Hilbert矩阵:

         

   这是一个著名的病态问题。通过首先给定解（例如取为各个分量均为1）再计算出右端的办法给出确定的问题。

(1）选择问题的维数为6，分别用 Gauss消去法、J迭代法、GS迭代法和SOR迭代法求解方程组,其各自的结果如何?将计算结果与问题的解比较,结论如何。

(2）逐步增大问题的维数，仍用上述的方法来解它们，计算的结果如何?计算的结果说明的什么?

(3）讨论病态问题求解的算法。

实验目的:通过本实验加深对于高斯消去法，Jacobi迭代法，G-S迭代法和SOR迭代法的理解和运用，同时理解不同阶数对于方程的影响，同时加深对于病态方程的理解。

实验原理:

（1）高斯消去法
高斯消去法是一种用于解线性方程组的数值方法，其原理基于初等行变换和回代。

假设给定一个线性方程组 AX=b，其中 A 是一个 n×n 的系数矩阵，X 和 b 分别是未知数向量和常数向量。高斯消去法的主要步骤如下：

1.构建增广矩阵：将系数矩阵 A 和常数向量 b 合并成一个增广矩阵 [A | b]。

2.消元过程：通过一系列的初等行变换将增广矩阵转化为上三角形矩阵。这些初等行变换包括以下操作：

3.交换两行的位置；

4.用一个非零常数乘以某一行的所有元素；

5.用一行的倍数加到另一行上。

在消元过程中，每一步都以一个主元为基准，将主元以下的列中的元素通过消元操作变为零，以实现逐步消去下方的元素。

回代过程：从上三角形矩阵的最后一行开始，通过回代求解未知数的值。回代的步骤如下：

求解最后一行的未知数；继续向上一行回代，依次求解每个未知数，直到求解出所有未知数。回代过程中，每个未知数的解是通过将已知的未知数代入方程进行求解得到的。

得到方程组的解：回代过程完成后，我们得到了线性方程组的解向量 X。

高斯消去法的关键思想是通过消元操作将线性方程组转化为上三角形矩阵，从而使回代过程更加简单和可行。它的优点是简单易实现，但它的缺点是可能会面临主元为零或接近零的情况，导致算法的稳定性下降，需要进行一些修正，如选取主元时使用行部分选主元（部分主元消去法）或使用列部分选主元（完全主元消去法）。

    这里还有LU分解的过程：

对于 （A非奇异）求解时，可以先将A分解成一个下三角矩阵L和一个上三角矩阵U的乘积，即 ，就可以通过

                               

求解出 的值。

欲把一个给定的矩阵A分解为一个下三角阵L与一个上三角阵U的乘积，最自然的做法便是通过一系列的初等变换，逐步将A约化为一个上三角阵，而又能保证这些变换的乘积是一个下三角阵。这可归结为：对于一个任意给定的向量 找一个尽可能简单的下三角阵，使 经这一矩阵作用之后的第 至第 个分量均为零。能够完成这一任务的最简单的下三角阵便是如下形式的初等下三角阵：

                                

其中

                           

即

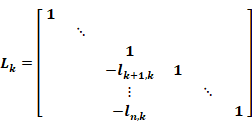
这种类型的初等下三角阵称作Gauss变换，而称向量 为Gauss向量。

对于一个给定的向量 我们有：

由此立即可知，只要取

                            

便有

                           

当然，这里我们要求 

而后经过多次变换可以得到

                               

从而求出上三角阵U，而后通过