博客介绍了用C++刷OJ题的细节，如输入输出效率、最值使用等。还给出30道算法题的解法，包括动态规划、贪心、模拟等，如最小花费爬楼梯、数组中两字符串最小距离等，同时提及各题的复杂度、注意事项及代码思路。
OJ细节注意事项
用C++刷题的时候，cin和cout的时间效率是不如scanf和printf的，如果输入输出的数据量非常大时，建议使用scanf和printf，不然有可能算法没问题但是还是超时了。
另外，有时候我们使用最大值或者最小值的时候，可以不用INT_MAX或者INT_MIN。有时候会导致数据溢出而报错，最大值可以使用 0x3f3f3f3f，最小值可以使用-0x3f3f3f3f。（4个3f）。
1.最小花费爬楼梯
（大部分题都可以在牛客网中直接搜到得到）
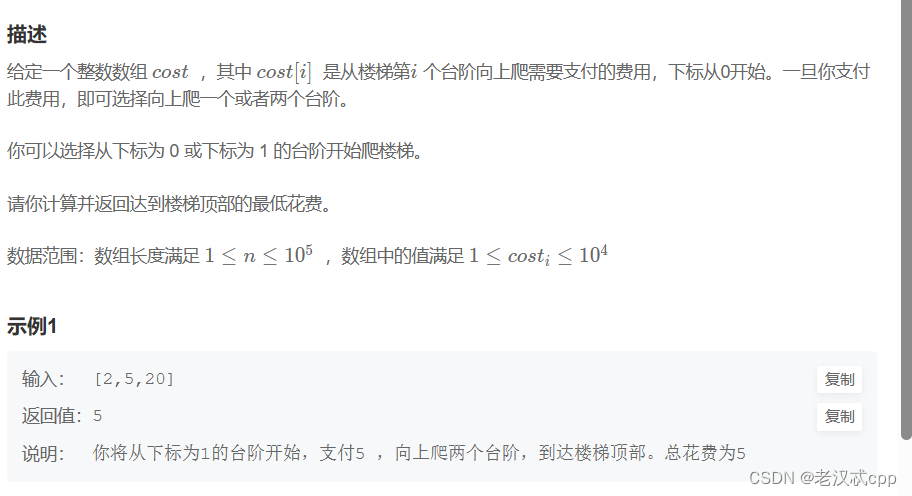
这是一道很经典且基础的动态规划的题目。
1.首先我们来分析状态表示，我们可以根据经验来发现这是一个线性dp，我们可以定义一个数组，以i位置为结尾，表示到这个位置所需要的最小花费。
2.再来分析状态转移方程，既然知道以i为结尾表示到这个位置的最小花费，那么它该怎么表示呢？据题意发现，它可以从i - 1这个位置跳上来，也可以从i - 2这个位置跳上来，一共就这两种情况，所以状态转移方程： dp[i] = min(dp[i - 1] + cost[i - 1],dp[i - 2] + cost[i - 2])。
3.注意一下填表顺序，因为我们填表的时候依赖的是 i - 1和i - 2这个位置的，所以填表顺序是从左往右。
4.初始化，因为由题意可得，我们可以从0或者1下标的台阶开始，所以dp[0]和dp[1]都可以初始化为0。
至此算法原理就到这里结束了
代码（核心代码模式）：
int minCostClimbingStairs(vector<int>& cost) {
int n = cost.size();
vector<int> dp(n + 1);
for(int i = 2; i <= n; ++i)
{
dp[i] = min(dp[i - 1] + cost[i - 1],dp[i - 2] + cost[i - 2]);
}
return dp[n];
}
不过要注意，我们的dp数组要多开一个，因为我们要跳到第n个台阶才算结束。
2.数组中两个字符串的最小距离
解法一：暴力解法
直接两层for循环，进行暴力枚举，这样的话时间复杂度为O（N^2)，一般会超时。
解法二：贪心
我们可以定义两个变量，分别为prev1和prev2，分别代表从左向右遍历时，str1最后出现的位置和str2最后出现的位置，这样的话我们在遍历的时候，一边更新结果ret，一边更新str1或者str2最后出现的位置，我们把这种方式称为预处理。时间复杂度为O（N）。
代码
#include <iostream>
using namespace std;
int main()
{
int n;
string s1,s2;
string s; // 这里就不定义数组了，每输入一个就处理一个
cin >> n >> s1 >> s2;
int prev1 = -1;
int prev2 = -1;
int ret = 0x3f3f3f3f;
for(int i = 0; i < n; ++i)
{
cin >> s;
if(s == s1)
{
if(prev2 != -1)
{
ret = min(ret,i - prev2);
}
prev1 = i;
}
else if(s == s2)
{
if(prev1 != -1)
{
ret = min(ret,i - prev1);
}
prev2 = i;
}
}
cout << (ret == 0x3f3f3f3f ? -1 : ret) << endl;
return 0;
}
3.dd爱框框
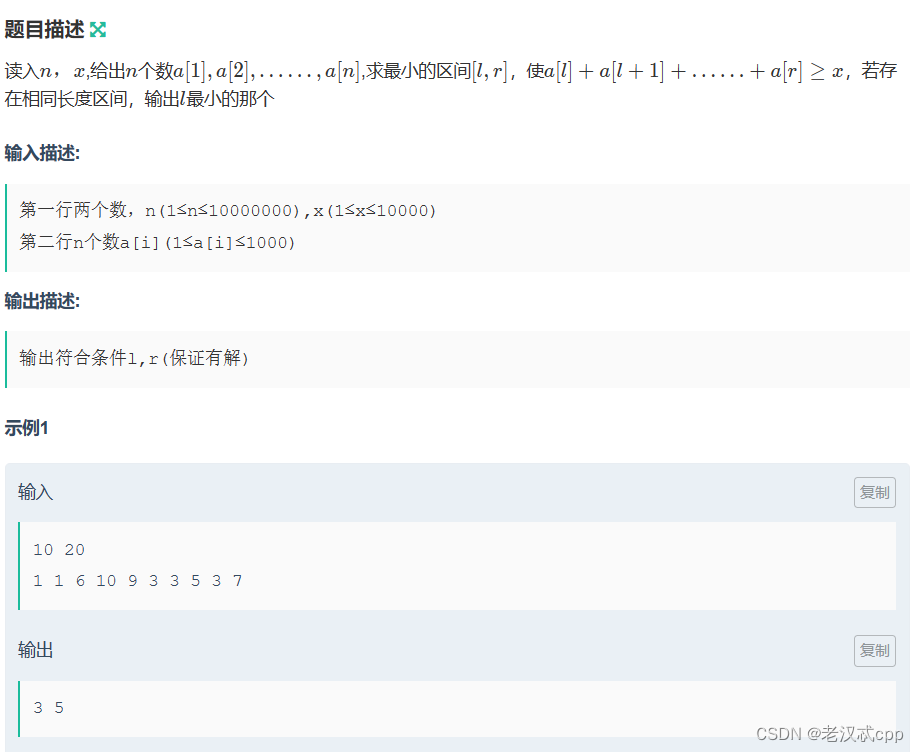需要注意的是，它的下标是从1开始的。
解法一：暴力解法
定义两个指针，两层for循环，从左往右先固定left（left从0开始），向后暴力枚举，时间复杂度为O（N^2)。
解法二：滑动窗口
使用滑动窗口要特别注意，这道题所给的数组的元素的大小是大于0的！如果小于0就不能使用滑动窗口了，因为它不满足单调性了。
算法流程：
因为滑动窗口的思想是两个指针同时向右移动，当sum >= x时，left向右移，使得sum减小，当sum < x 时，right右移，使得sum增大，这样的遍历方式具有单调性，可以使用滑动窗口，但如果有元素的值小于0，那么left向右移的时候既可能增大又可能减小，不满足单调性，此时就不再适用滑动窗口了。
代码：
#include <iostream>
#include <vector>
using namespace std;
int main()
{
int n,x;
cin >> n >> x;
vector<int> v(n);
int sum = 0;
for(int i = 0; i < n; ++i)
{
cin >> v[i];
}
int l = 0,r = 0;
int left = 0,right = 0;
int ret = 0x3f3f3f3f;
while(right < n)
{
if(sum < x)
{
sum += v[right];
right++;
}
else
{
if(ret > right - left)
{
l = left;
r = right - 1;
ret = right - left;
}
sum -= v[left];
left++;
}
}
// 因为题意里的下标是从数组的1开始的
cout << (l + 1) << " " << (r + 1)<< endl; // 注意下标的映射关系
return 0;
}
4.杨辉三角
这是一道很简单的线性dp问题。
解法：
状态表示：定义一个int dp[31][31]，其中dp[i][j]表示第i行第j列的值。
状态转移方程：dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]。
初始化：可以将dp[0][0]初始化成1。
填表顺序：从上往下，从左往右。
返回值：据题意，按宽5直接打印每一行。
代码：
#include <iostream>
using namespace std;
int main()
{
int n;
cin >> n;
int dp[31][31] = {0};
dp[0][0] = 1;
for(int i = 1; i <= n; ++i)
{
for(int j = 1; j <= i; ++j)
{
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
printf("%5d",dp[i][j]);
}
cout << endl;
}
return 0;
}
5.孩子们的游戏
题目描述非常的繁琐，其实就是约瑟夫环问题。
解法一：模拟
我们可以用双向环形链表，非常简单就能完成。
或者也可以用一个bool数组，下标对应孩子的编号，主要也是环形数组的概念。
时间复杂度为O(n)，空间复杂度为O(n)。
解法二：动态规划
1.状态表示：可以用dp[i]表示有i个孩子围在一起，获胜的那个孩子的编号。
2.状态转移方程：
假设dp[n]，m。 首先我们找到m - 1的下标，将这个孩子删掉。然后m - 1的下一个是m。将m 的下标重新标识为0，那么m + 1 就是1，依次类推
此时孩子数变成了n - 1，所以dp[n] 与 dp[n - 1] 的关系，也就是下标的映射关系。
所以dp[n] = (dp[n - 1] + m) % n。
所以状态转移方程 dp[i] = (dp[i - 1] + m) % n。
因为dp[i]它依赖的是dp[i - 1]，所以我们可以利用空间优化，将空间复杂度降为O(1)。
代码
int LastRemaining_Solution(int n, int m) {
int f = 0;
for(int i = 1; i <= n; ++i)
{
f = (f + m) % i;
}
return f;
}
6.链表相加（二）
解法：模拟
主要分为 逆序 + 高精度相加。
我们可以创建一个虚拟头结点，先将两个链表逆置一下，方便相加。然后再采用头插法将结果插入到新链表中。
代码
class Solution {
public:
ListNode* addInList(ListNode* head1, ListNode* head2) {
int t = 0;
ListNode* cur1 = ListReverse(head1);
ListNode* cur2 = ListReverse(head2);
ListNode* ret = new ListNode(-1);
while(cur1 || cur2 || t)
{
if(cur1)
{
t += cur1->val;
cur1 = cur1->next;
}
if(cur2)
{
t += cur2->val;
cur2 = cur2->next;
}
ListNode* tmp = new ListNode(t % 10);
t /= 10;
tmp->next = ret->next;
ret->next = tmp; // 直接使用头插法，完事后就可以直接返回结果
}
cur1 = ret->next;
delete ret;
return cur1;
}
ListNode* ListReverse(ListNode* head) // 头插逆置
{
ListNode* newHead = new ListNode(-1);
ListNode* cur = head;
while(cur)
{
ListNode* next = cur->next;
cur->next = newHead->next;
newHead->next = cur;
cur = next;
}
cur = newHead->next;
delete newHead;
return cur;
}
};
7.大数乘法
解法：
主要还是模拟解法。需要注意的是要先无进位相乘，然后再统一作进位。
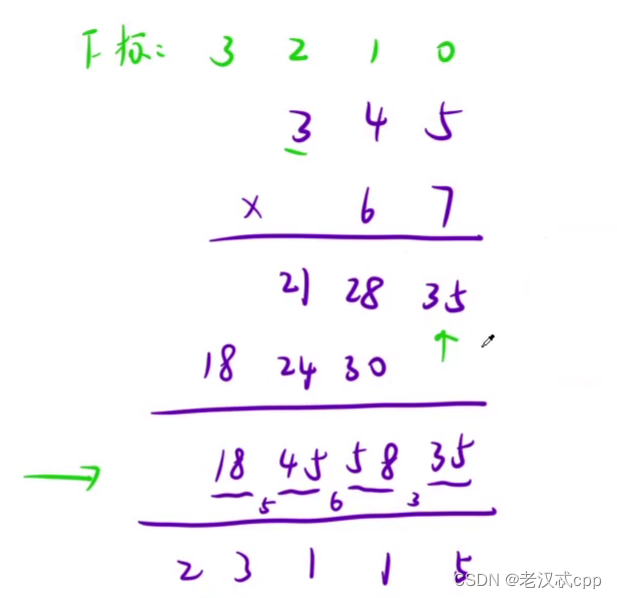
并且，我们要对每一个进位用下标进行标记，方便进行累加。
算法流程：
首先先将两个字符串进行逆置，方便相加，再创建一个数组，数组的大小是两个字符串的长度相加，这样保证了最终结果的长度不会超过数组的长度。
不过后续也要处理前导零问题。
代码：
class Solution {
public:
string solve(string s, string t) {
int n = s.size();
int m = t.size();
reverse(s.begin(),s.end());
reverse(t.begin(),t.end());
vector<int> tmp(m + n);
for(int i = 0; i < n; ++i)
{
for(int j = 0; j < m; ++j)
{
tmp[i + j] += (s[i] - '0') * (t[j] - '0');
}
}
string ret;
int c = 0;
for(auto x : tmp)
{
c += x;
ret += (c % 10) + '0';
c /= 10;
}
// 因为我们给tmp数组开的大小是m + n，因为两数相乘之后的位数绝对不会超过m + n
// 但是也有可能存在前导零，需要去除。
while(ret.size() > 1 && ret.back() == '0')
ret.pop_back(); // 因为ret还没逆置，所以如果有前导零也在末尾
reverse(ret.begin(),ret.end());
return ret;
}
};
8.最小公倍数
题目非常简单，就是求最小公倍数。
如果我们直接使用循环的方式来求出结果，那么这里是会超时的。
因此这里需要用到一些数学基础，我们将公式记下后，以后作为结论使用即可。
假设我们要求a和b的最小公倍数，那么设函数lcm(a,b)。设求a和b的最小公约数为gcd(a,b)。
那么公式 lcm(a,b) = a * b / gcd(a,b)。那么我们只要求出最小公约数即可。
代码
#include <iostream>
using namespace std;
int gcd(int a,int b)
{
if(b == 0)
return a;
return gcd(b,a % b);
}
int main()
{
int a,b;
cin >> a >> b;
cout << (a * b / gcd(a,b)) << endl;
return 0;
}
9.最长回文子串
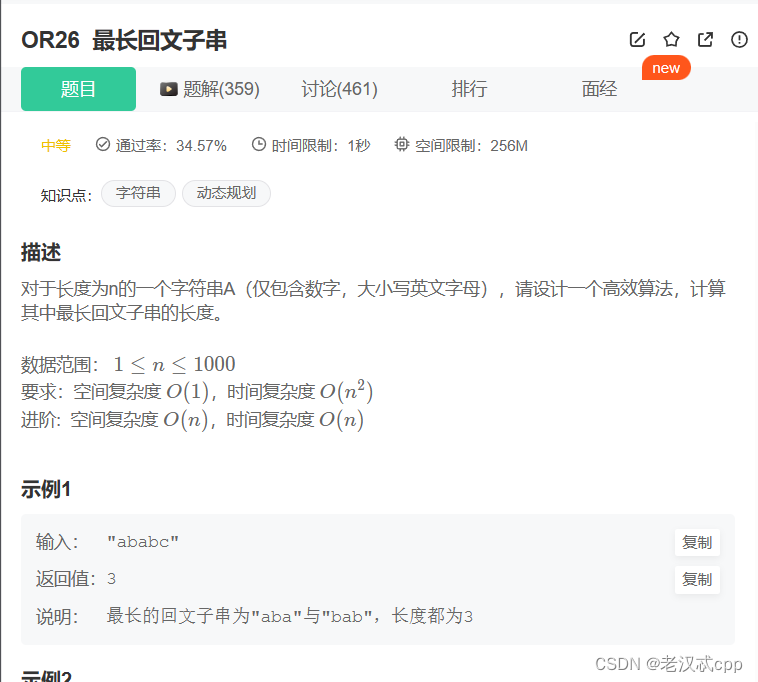首先需要注意的是，子串必须是挨在一起的，不能中间隔着字符。
解决这道题有三种做法：
1.动态规划：时空复杂度为，O(n^2),O(N^2)。
2.马拉车算法:时空复杂度为,O(n),O(n)。
3.中心扩展算法：时空复杂度为O(n^2),O(1)。
因为马拉车算法带有局限性，只能解决回文串问题，这里使用中心扩展算法。
中心扩展算法基本流程：
从0下标开始，依次枚举S[i]。然后再定义两个指针left和right，如果S[left] == S[right]，那么两个指针就同时向两边移动，直到越界或者二者不相等
有两个细节问题：
1.计算长度，每次记得取回文串的最大值，用ret表示最终结果，当两个指针停下来的时候，长度可表示为len = right - left - 1。那么记得要ret = max（ret， right - left - 1）。
2.回文串有奇数长度和偶数长度，对于这两种情况，我们再每次枚举的时候都要对这两种情况进行计算，取二者的最大值。
代码
class Solution
{
public:
int getLongestPalindrome(string A)
{
int n = A.size();
int ret = 1;
for(int i = 0; i < n; ++i)
{
// 先枚举奇数情况
int left = i - 1;
int right = i + 1;
while(left >= 0 && right < n && A[left] == A[right])
{
left--;
right++;
}
if(A[left + 1] == A[right - 1])
ret = max(ret,right - left - 1);
// 然后枚举偶数情况
left = i - 1;
right = i;
while(left >= 0 && right < n && A[left] == A[right])
{
left--;
right++;
}
if(A[left + 1] == A[right - 1])
ret = max(ret,right - left - 1);
}
return ret;
}
};
10.买卖股票的最好时机（一）
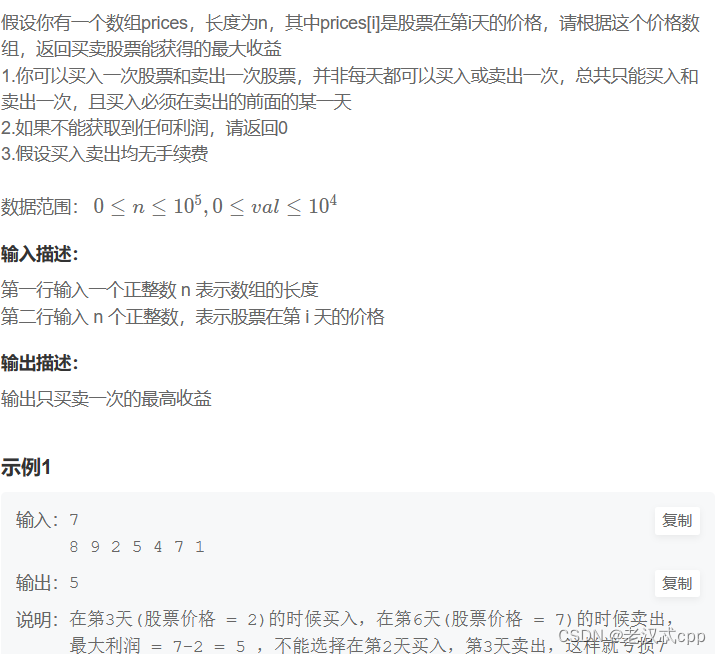这道题也可以用动态规划来解决，但是贪心还是容易许多。
贪心算法流程：
首先用i枚举n天的股票价格，用变量num来记录在i之前的股票的最小值（也可以最大值）来作为买入值，用变量ret来表示最大利润，那么每次枚举时只需要计算： 第i天的股票价格 - 之前的最小值（买入值），然后更新ret即可。
代码
#include <climits>
#include <iostream>
using namespace std;
int main()
{
int n;
cin >> n;
int ret = 0;
int minp = INT_MAX;
int price;
for(int i = 0; i < n; ++i)
{
cin >> price;
minp = min(minp,price);
ret = max(ret,price - minp);
}
cout << ret << endl;
return 0;
}
时空复杂度为：O（N），O（1）。空间复杂度上做了优化，所以是O（1）。
11.游游的水果大礼包
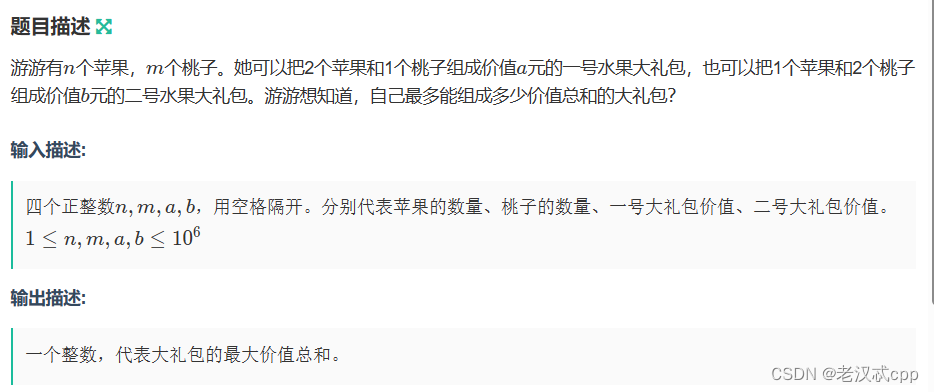
易错：这道题不能使用贪心，只能用枚举
算法流程：
n个苹果，m个桃子，如果一号水果礼包的个数选择了x个，二号水果礼包的个数选择了y个，那么价值总和为ax + by。而x = min（n/2，m），那么在这个基础上y = min（n - x * 2，（m - x） / 2）。带入到ax + by中就可以计算出该次选择的价值总和，我们枚举所有情况，取其中的最大值即可。
代码
#include <iostream>
using namespace std;
int main()
{
int n,m,a,b;
cin >> n >> m >> a >> b;
long long ret = 0;
for(long long i = 0; i <= min(n / 2,m); ++i) // 这里是枚举礼包1
{
long long y = min(n - i * 2,(m - i) / 2);
ret = max(ret,a * i + b * y);
}
cout << ret << endl;
return 0;
}
12.买卖股票的最好时机（二）
这道题用贪心解法很快，并且可以达到空间复杂度为O（1）。
贪心算法流程：
定义一个变量prev来记录前一天的股票价格，只要发现具有上涨趋势，直接卖出，将利润相加。
#include <iostream>
using namespace std;
int main()
{
int n;
cin >> n;
int ret = 0;
int prev = -1;
for(int i = 0; i < n; ++i)
{
long long tmp;
cin >> tmp;
if(prev != -1)
{
if(prev <= tmp)
ret += tmp - prev;
}
prev = tmp;
}
cout << ret << endl;
return 0;
}
时空复杂度为O（N），O（1）。
13.重排字符串
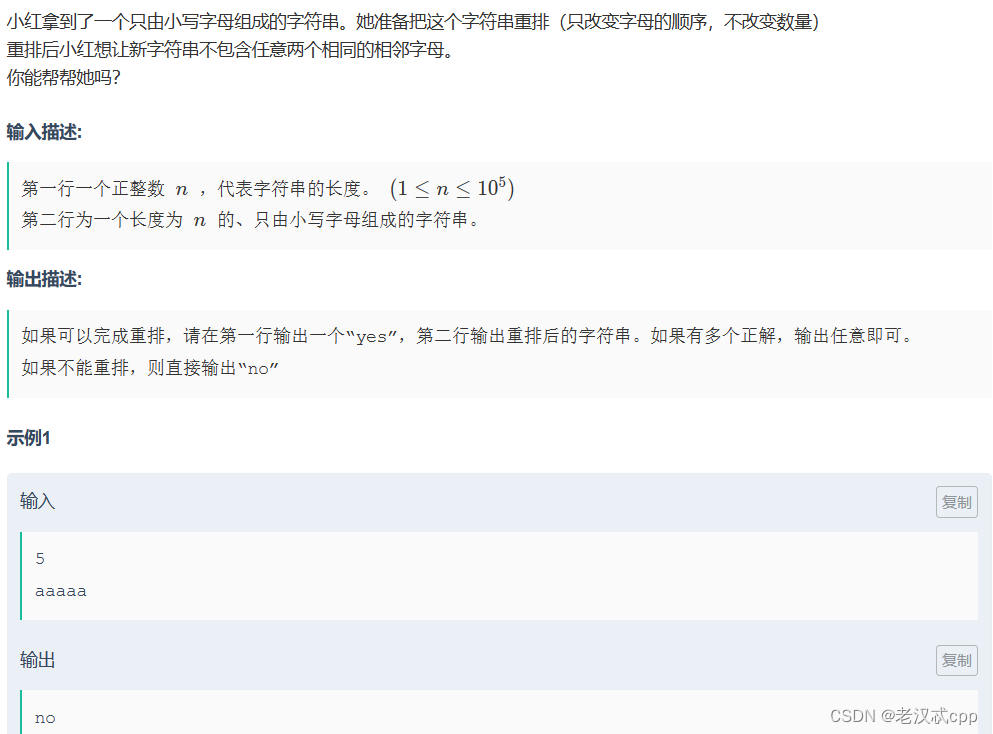
注意：这道题的输出分为两种情况，并且如果是yes的话，还需要我们将结果进行打印。
解法：贪心。
算法流程：
解决这道题，我们可以通过三条规则来指导我们写代码
1.每次只处理相同的一批字符，比如aabb，那我们先把字符'a'全部处理完再处理字符b。
2.最先处理出现次数最多的字符。
3.每次摆放字符的时候，间隔一个格子。
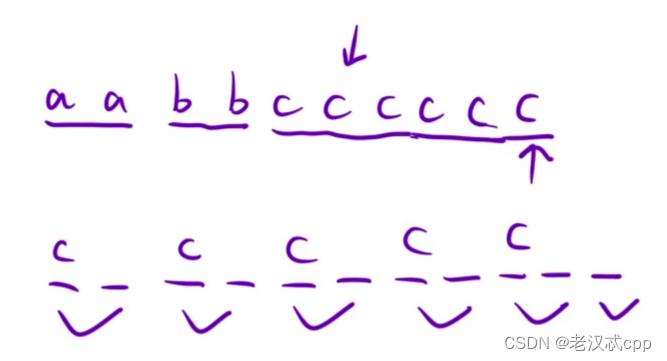
图中我们发现，只要先处理好出现次数最多的字符，将他们间隔一个格子进行摆放，如果摆放成功的话，那么我们发现就可以做到相邻的字符不相等。
所以，能不能重排的条件就是：假设有n个字符，c字符出现次数最多，为maxcount，如果maxcount <= (n + 1) / 2，那么就可以重排。
注意细节：我们可以先让c字符从偶数格子上开始填，如果能重排，那么一定可以把c字符给填完。接着填剩下的字符，如果偶数的格子填满了，记得要将下标置为1，然后从奇数位置开始填，直到填满。
这道题还比较考验代码能力。
代码：
#include <iostream>
using namespace std;
int cnt[26] = {0};
const int N = 1e5 + 10;
char s[N];
char ret[N];
int main()
{
int n;
cin >> n >> s;
int maxcount = 0;
char maxch;
for(int i = 0; i < n; ++i)
{
int index = s[i] - 'a';
cnt[index]++;
if(cnt[index] > maxcount)
{
maxcount = cnt[index];
maxch = s[i];
}
}
if(maxcount > (n + 1) / 2) cout << "no" << endl;
else
{
cout << "yes" << endl;
// 先优先处理出现次数最多的字符
int i = 0; // 先从偶数开始填，中间间隔一个字符的填
while(cnt[maxch - 'a']--)
{
ret[i] = maxch;
i += 2;
}
for(int j = 0; j < 26; ++j)
{
while(cnt[j] > 0)
{
if(i >= n) i = 1; // 偶数填完了就从奇数开始
ret[i] = j + 'a';
i += 2;
cnt[j]--;
}
}
for(int j = 0; j < n; ++j) cout << ret[j];
cout << endl;
}
return 0;
}
14.删除相邻数字的最大分数
这道题的解法是用动态规划
但是在动态规划之前，我们需要先对数组进行处理，据题意可得，我们可以定义一个10^4大小的数组tmp，它的每个元素表示它的下标出现的总分数。
接着就是动态规划了，对于i位置，有两种情况：
1.选择该位置并相加，那么dp1[i] = tmp[i] + dp2[i - 1]
2.不选择该位置，那么dp2[i] = max(dp1[i - 1],dp2[i - 1]。
由此可见我们需要定义两个dp数组。
初始化我们只需要将dp1[0]和dp2[0]初始化为0即可，返回dp1[10^4 - 1]和dp2[10^4 - 1]的最大值即可。
代码：
#include <iostream>
#include <vector>
using namespace std;
const int N = 1e4 + 10;
int main()
{
int arr[N] = {0};
int n;
cin >> n;
vector<int> v(n);
for(int i = 0; i < n; ++i)
{
cin >> v[i];
arr[v[i]] += v[i];
}
vector<int> dp1(N); // 表示选择i位置的值
vector<int> dp2(N); // 表示不选择i位置的值
for(int i = 1; i < N; ++i)
{
dp1[i] = arr[i] + dp2[i - 1];
dp2[i] = max(dp1[i - 1],dp2[i - 1]);
}
cout << max(dp1[N - 1],dp2[N - 1]) << endl;
return 0;
}
15.分组
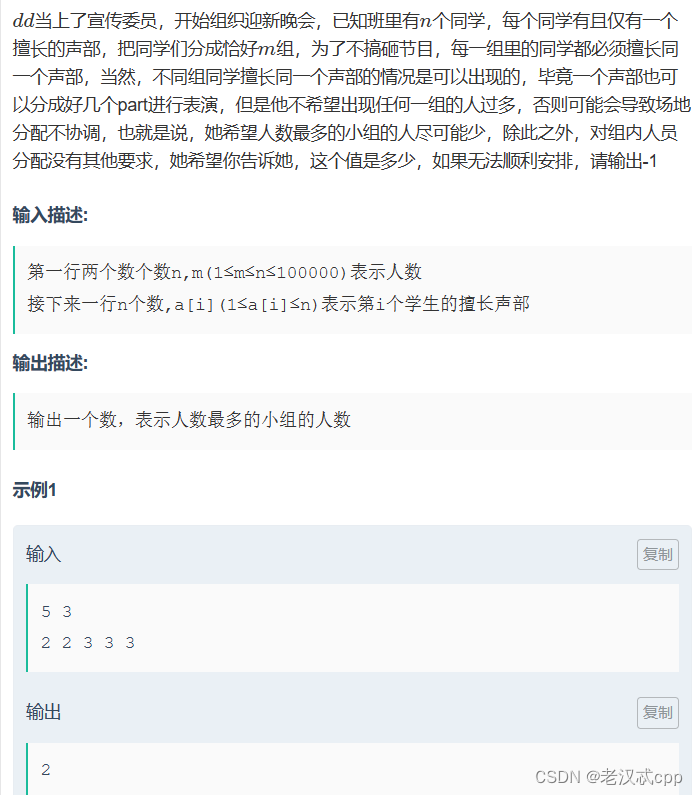这道题有点复杂，有n个同学，需要分成m组，其中分到每一组的同学会的声部必须是相同的，需要我们求在能满足分m组的情况下，尽量地使人数最多的组人数最少。
看起来确实有点绕。
比如示例中要分成3组，我们可以分成 2 2 333，这样人数最多的组的人数就是3个人，但是还有一种分法：22 3 33，这样人数最多的组就只有2人了，因此答案就是2。
那么这道题的解法就是枚举 + 二分，也就是在暴力枚举的基础上用二分法进行优化。
算法流程：
首先解决这道题，我们需要先将会某一种声部的同学的人数统计起来，可以用哈希表来进行统计。
hash[i]表示会声部i的同学的个数。
假设我们的最终结果是x，也就是每一组最多分x个人，那么i声部可以分为 hash[i] / x + (hash[i] % x == 0 ? 0 : 1)个组，那么接着我们只需要用这个x来枚举hash[i]，将计算结果相加，如果 小于等于 m，说明它可以分组，既然是要求最多人数组的最小值，那么我们可以从1开始枚举，一直枚举到哈希表中的最大值，一旦出现 sum <= m的情况，说明它就是结果，如果全部枚举完也没有结果，那么就返回-1。到这里就是暴力枚举的结果，我们在枚举的时候，可以发现其中的二段性，于是可以加入二分法来进行优化。
代码：
#include <iostream>
#include <unordered_map>
using namespace std;
int main()
{
int n,m;
cin >> n >> m;
unordered_map<int, int> hash;
int maxnum = 0;
for(int i = 0; i < n; ++i)
{
int tmp;
cin >> tmp;
hash[tmp]++;
if(hash[tmp] > maxnum)
maxnum = hash[tmp];
}
int left = 1;
int right = maxnum;
int ret = -1;
while(left <= right)
{
int mid = (right - left) / 2 + left;
//int mid = left;
int count = 0;
for(auto& pair : hash)
{
count += pair.second / mid + (pair.second % mid == 0 ? 0 : 1);
}
if(count <= m)
{
ret = mid;
right = mid - 1;
}
else left = mid + 1;
//left = mid + 1;
//left++;
}
cout << ret << endl;
return 0;
}
16.拓扑排序
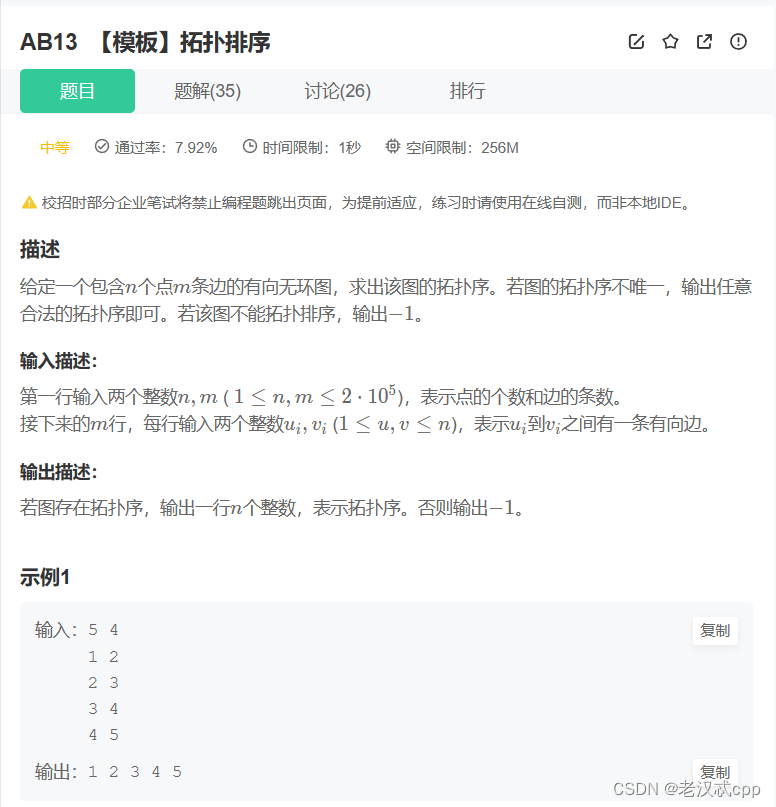是一道很基础的拓扑排序。
算法流程：
首先构建图，可以选用矩阵或者邻接表。还要记得统计入度信息。
需要借助一个队列，首先将入度为0的点插入到队列中，然后BFS，每遍历到一个点，就将这个点指向的点的入度进行 -- 。如果减到0，就将它插入到队列中。可以用一个数组来统计结果，如果这个数组的大小不等于n，说明不能进行拓扑排序，输出-1，否则打印结果。另外牛客网的这道题的测试用例非常ex，在输出结果的最后一个数字后面不能带空格，否则结果会出错。
代码：
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
const int N = 2e5 + 10;
vector<vector<int>> edges(N); // 用邻接表构建图
int in[N]; // 统计入度信息
int main()
{
queue<int> q;
int n,m;
cin >> n >> m;
for(int i = 0; i < m; ++i)
{
int a,b;
cin >> a >> b;
edges[a].push_back(b);
in[b]++;
}
for(int i = 1; i <= n; ++i)
{
if(in[i] == 0)
q.push(i);
}
vector<int> ret;
while(q.size())
{
int tmp = q.front();
ret.push_back(tmp);
q.pop();
for(auto& x : edges[tmp])
{
in[x]--;
if(in[x] == 0)
q.push(x);
}
}
if(ret.size() != n) cout << -1 << endl;
else
{
for(int i = 0; i < n -1 ; ++i)
cout << ret[i] << " "; // 测评非常恶心，如果最后一个输出后有空格就不通过
cout << ret[n - 1] << endl;
}
return 0;
}
17.神奇数
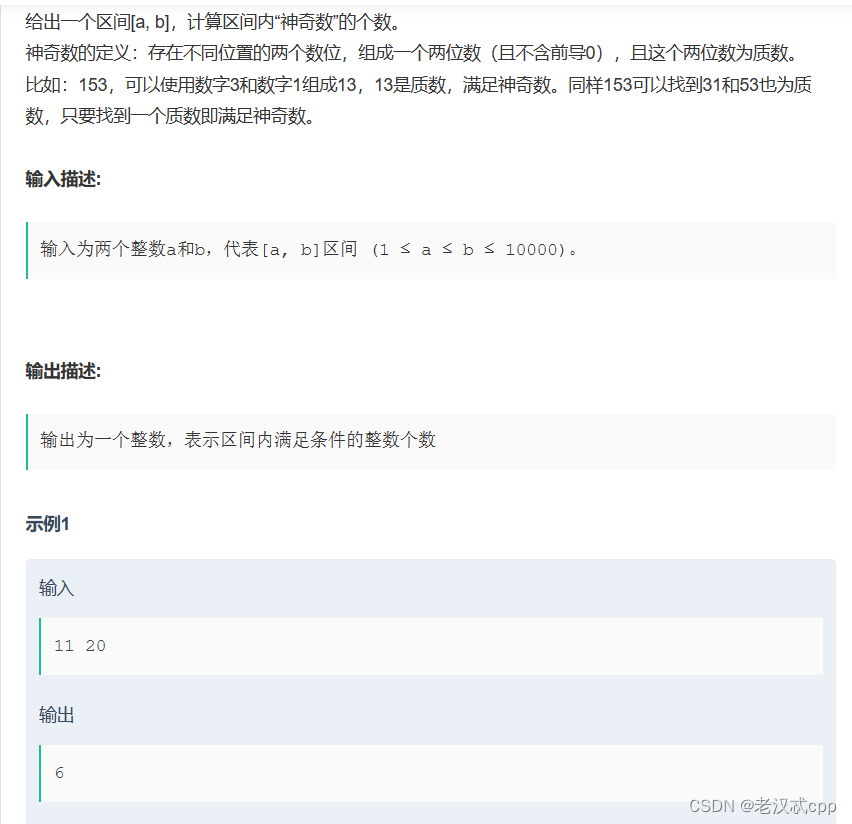
这道题的解法是：枚举 + 判断是否是质数
对于一个数，我们只需要拿到这个数的任意两位，然后判断这两位是否是质数，如果是那么就符合题意的神奇数。
算法流程：
从a到b进行枚举，首先可以定义一个数组，将i的每一位数存到数组中， 这样方便我们拿到i的每一位数。
另外枚举的时候有一个细节，那就是a至少得是两位数，一位数是不能充当神奇数的。
关于质数的判断，我们也是用依次枚举来判断的，每次除以一个数，如果能整除那么就不是质数，否则就是质数，另外我们还可以进行优化，对于依次枚举数来除以目标判断数，枚举数的最大值可以取sqrt(n) + 1，也就是它的平方根 + 1。这样可以减少判断次数。
最后在枚举判断神奇数的时候，注意十位和个位的数不能是数组中的同一个数，而且不能有前导零。
代码：
#include <iostream>
#include <vector>
#include <math.h>
using namespace std;
int a,b;
bool isprime(int n)
{
for(int i = 2; i < sqrt(n) + 1; ++i)
{
if(n % i == 0)
return false;
}
return true;
}
int check(int n)
{
vector<int> num;
while(n)
{
num.push_back(n % 10);
n /= 10;
}
int sz = num.size();
for(int i = 0; i < sz; ++i) // 这里枚举十位
{
for(int j = 0; j < sz; ++j) // 枚举个位
{
if(j != i && num[i] != 0) // i j不能枚举同一个数
{
if(isprime(num[i]*10 + num[j]))
return 1;
}
}
}
return 0;
}
int main()
{
cin >> a >> b;
int ret = 0;
for(int i = max(a,10); i <= b; ++i)
{
ret += check(i);
}
cout << ret << endl;
return 0;
}
18.01背包问题（模板）
背包问题的解法就是动态规划
算法流程：
dp[i[[j]，i表示第i个物品，j表示当前的体积大小。
所以状态表示就是dp[i][j]表示从前i个物品中选择，总体积不超过j，此时的质量最大值。
状态转移方程：对于第i个位置的物品有两种情况，一是选择这个物品，二是不选择这个物品。
如果不选择i物品，那么dp[i][j] = dp[i - 1][j]。
如果选择i物品,且j要大于i物品的体积：dp[i][j] = dp[i - 1][j - i物品的体积] + i物品的质量。
选择二者的最大值，并且要注意后者还有一个条件，就是当前的j要大于i物品的体积。
初始化：我们可以多开一个空间，从下标1位置开始填，0位置初始化为0。
返回值：直接返回dp表的最后一个值即可。
代码：
class Solution {
public:
int knapsack(int V, int n, vector<vector<int> >& vw) {
vector<vector<int>> dp(n + 1,vector<int>(V + 1));
for(int i = 1;i <= n; ++i)
for(int j = 1; j <= V; ++j)
{
dp[i][j] = dp[i - 1][j]; // 不选
if(j >= vw[i - 1][0])
dp[i][j] = max(dp[i][j],dp[i - 1][j - vw[i - 1][0]] + vw[i - 1][1]);
}
return dp[n][V];
}
};
时空复杂度为O（n * V），O（n * V）
另外它还可以进行空间优化，可以将空间复杂度优化到O(n)。优化原理就不细说了，大致就是因为dp表从上往下填，从左往右填，其中一行里面也可以从右往左填，因此我们可以将行去掉，变成一维数组。
注意，优化后的填表顺序是从右往左填，并且还可以进行一个小时间上的优化。
代码：
class Solution {
public:
int knapsack(int V, int n, vector<vector<int> >& vw) {
vector<int> dp(V + 1);
for(int i = 1;i <= n; ++i)
for(int j = V; j >= vw[i - 1][0]; --j)
{
dp[j] = max(dp[j],dp[j - vw[i - 1][0]] + vw[i - 1][1]);
}
return dp[V];
}
};
19.小易的升级之路
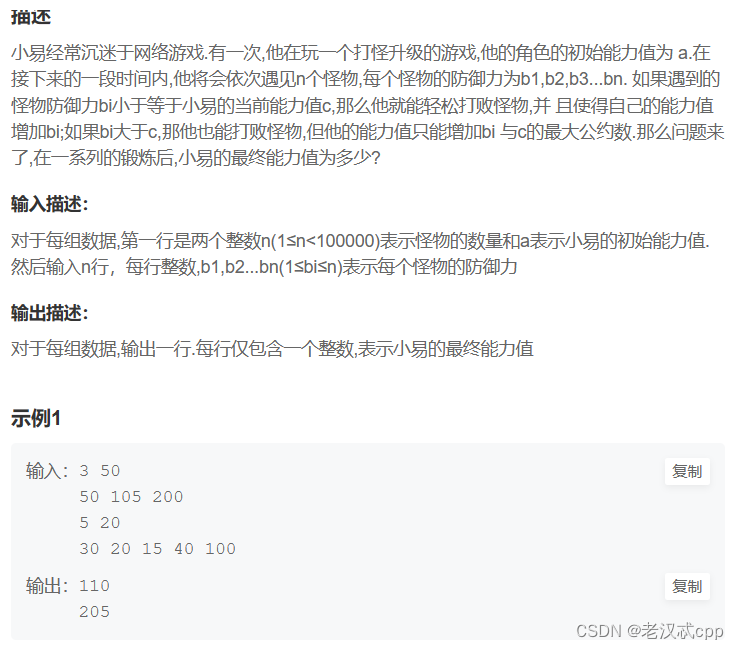
这是一道简单的模拟题，主要是考察求最大公约数的能力，如果直接使用循环遍历的方式求最大公约数，这里可能是会超时的。
假设求a，b的最大公约数，gcd(a,b)，那么gcd（a，b） = gcd（b，a%b）。用递归求解，递归出口就是当b == 0时， 返回a。
代码：
#include <iostream>
#include <vector>
using namespace std;
int gcd(int a,int b)
{
if(b == 0)
return a;
return gcd(b,a % b);
}
int main()
{
int n;
int a;
long long ret = 0;
int tmp;
while(cin >> n)
{
ret = 0;
cin >> a;
//vector<int> nums(n);
ret += a;
for(int i = 0; i < n; ++i)
{
cin >> tmp;
if(tmp > ret)
ret += gcd(ret,tmp);
else
ret += tmp;
}
cout << ret << endl;
}
return 0;
}
20.连续子数组最大和
这是一道很简单的线性dp问题。
状态表示：dp[i]，以i位置为结尾的子数组，它的和的最大值。
状态转移方程：dp[i] = max(dp[i - 1],0) + 当前的数组的值
初始化：因为我们要用到i - 1的位置，所以我们可以多开一个空间，将dp[0]初始化为0，这样不干扰后续的结果。
返回值：这里不能直接返回dp[n]，因为我们要找的是最大值，所以我们要返回dp过程中出现的最大值。
代码：
#include <climits>
#include <iostream>
#include <vector>
using namespace std;
int main()
{
int n;
int tmp;
int ret = INT_MIN;
cin >> n;
vector<int> dp(n + 1);
for(int i = 1; i <= n; ++i)
{
cin >> tmp;
dp[i] = max(dp[i - 1],0) + tmp;
ret = max(ret,dp[i]);
}
cout << ret << endl;
return 0;
}
21.非对称之美
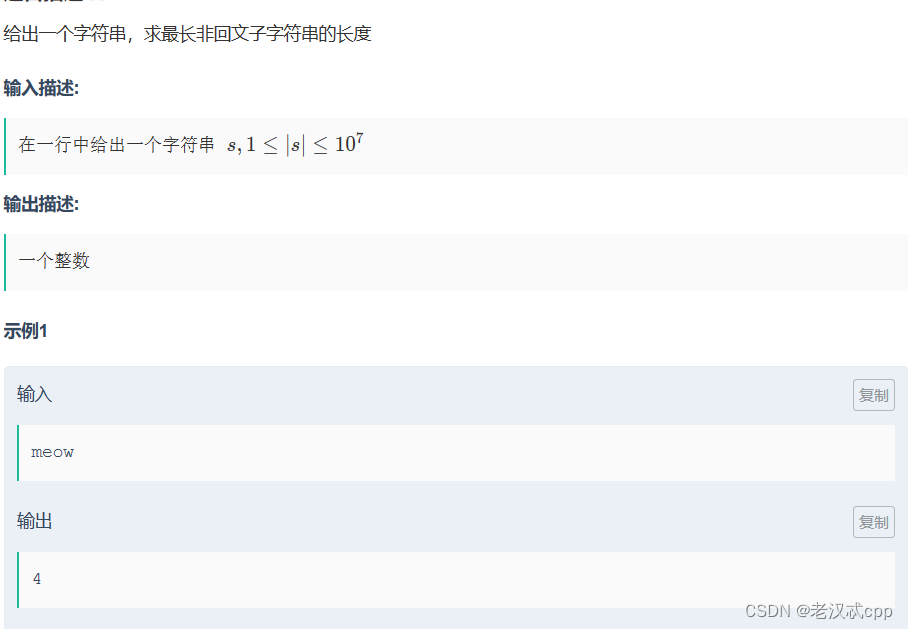
题意很简单，要求返回最长非回文子字符串的长度。
这道题不能使用做回文串的传统思路，传统思路的时间复杂度为O（n ^2)，这这个测试用例下大概会超时。因此我们可以用一个较为取巧的方法。
解法：找规律|贪心
算法流程：
假设字符串的总长度为sz。
因为它要求是要找最长的子字符串，那么我们直接先来判断整个字符串是否是回文串，如果是回文串，那么我们直接左右两边随便删掉一个字符，也就是sz - 1，那不就是最长的非回文子字符串了吗？如果它本来就是非回文字符串，那么返回sz即可。
另外会有一个特殊情况需要单独判断，那就如果字符串是类似aaaaaaa这样全是相同的字符串，那么我们需要单独判断一下，如果它是，直接返回0即可。
代码：
#include <iostream>
using namespace std;
int main()
{
string s;
cin >> s;
bool flag = false;
int sz = s.size();
for(int i = 1; i < sz; ++i)
{
if(s[i] != s[0])
{
flag = true;
break;
}
}
if(!flag) cout << 0 << endl;
else
{
int left = 0;
int right = sz - 1;
while(left <= right)
{
if(s[left] != s[right])
{
flag = false;
}
left++;
right--;
}
if(!flag) cout << sz<< endl;
else cout << sz - 1 << endl;
}
return 0;
}
22.最长回文子序列
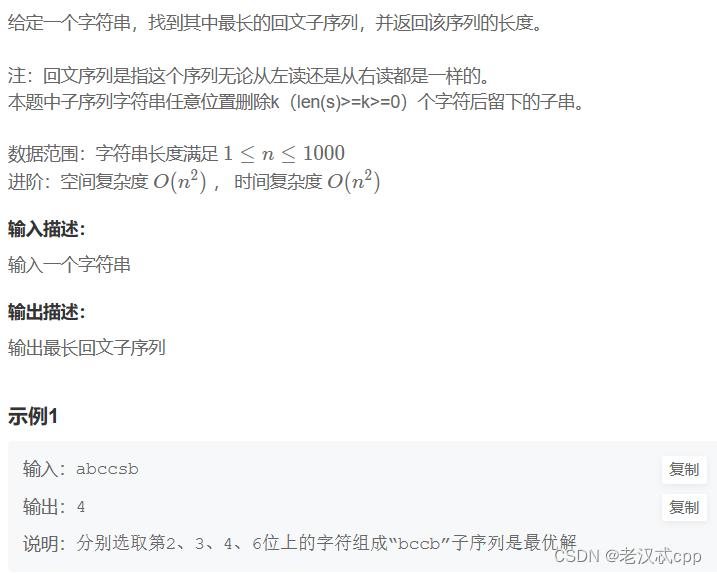这是一道入门的区域dp问题，当然也是线性dp。
注意这里求的是子序列，注意区分子序列和子串。
状态表示：
dp[i][j] 表示 s[i]到s[j]之间的最长回文子序列。
状态转移方程：
首先要注意i和j的位置问题：
1.i位置在前，j位置在后，那么如果i > j，说明这个位置是不合法的，那么此时dp[i][j] = 0
2.i == j。一个字符也能被看作一个回文串，因此此时dp[i][j] = 1。
3.i < j。其实以上两种都算是边界情况，需要特殊处理的或者注意的，当i < j 时，又有两种情况：
a.s[i] == s[j]，它俩相等，那么我们只需要用到 从i + 1 到 j - 1这个位置里面最长的回文子串再加上2即可。也就是 dp[i][j] = dp[i + 1][j - 1] + 2。
b.s[i] != s[j]，它俩不相等，那么此时 dp[i][j] = max(dp[i + 1][j],dp[i][j - 1])，也就是二者的最大值。
初始化：
在状态转移方程那里，我们对照着前两种情况，发现可以不用多开数组。
填表顺序：
这次的dp填表顺序不一样，填i的时候依赖的是 i + 1的位置，填j的时候依赖的是j - 1的位置。
因此填表顺序是从下往上，从左往右。
代码：
注意有个细节就是，j循环的起点是从i + 1位置开始的，因为之前说过了，i是要比j小的，另外在j循环前就让dp[i][i] = 1，这样j就可以从i + 1的位置开始了，并且在j循环里面不用每次再判断i是否等于j的情况。
#include <iostream>
#include <vector>
using namespace std;
int main()
{
string s;
cin >> s;
int n = s.size();
vector<vector<int>> dp(n,vector<int>(n));
for(int i = n - 1; i >= 0; --i) // i在前，j在后
{
dp[i][i] = 1; // 这样在j循环的时候就不用再判断 i是否等于j了。
for(int j = i + 1; j < n; ++j)
{
if(s[i] == s[j])
dp[i][j] = dp[i + 1][j - 1] + 2;
else
dp[i][j] = max(dp[i + 1][j],dp[i][j - 1]);
}
}
cout << dp[0][n - 1] << endl;
return 0;
}
23.判断是不是平衡二叉树
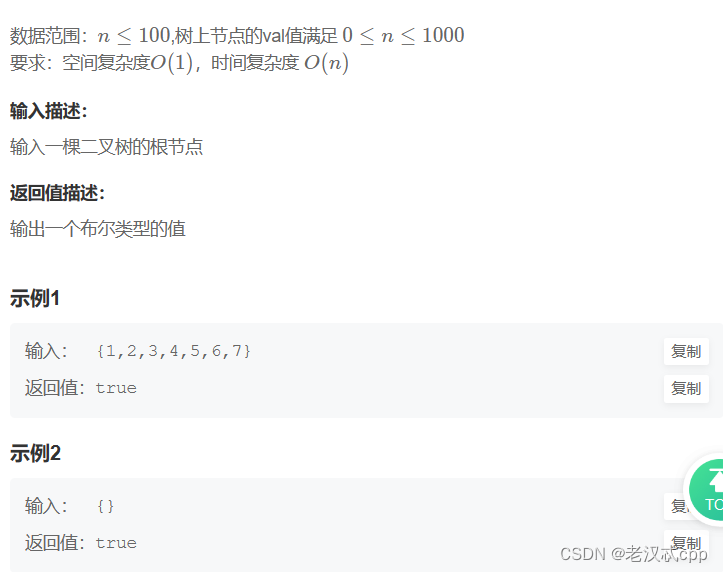
这题的解法就是递归，一般涉及到二叉树的题都是用递归解决的。
思路：
为了判断一个结点它是不是平衡二叉树，我们需要先求出它的左子树的高度，再求出它右子树的高度，如果它们两个相减的绝对值小于等于1，那么它就是平衡二叉树，我们需要返回true，否则返回false。
因此我们每次递归其实要返回两个信息，一个是字数的高度，而是它是否是平衡二叉树。在设计返回值上我们可以用一个int，如果int的值大于等于0，说明它表示的子树的高度，如果等于-1，说明它不是平衡二叉树。
代码：
class Solution {
public:
bool IsBalanced_Solution(TreeNode* pRoot) {
return dfs(pRoot) != -1;
}
int dfs(TreeNode* root)
{
if(root == nullptr) return 0;
int left = dfs(root->left);
if(left == -1) return -1; // 相当于剪枝了
int right = dfs(root->right);
if(right == - 1) return -1;
return abs(left - right) <= 1 ? max(left,right) + 1 : -1;
}
};
24.最大子矩阵
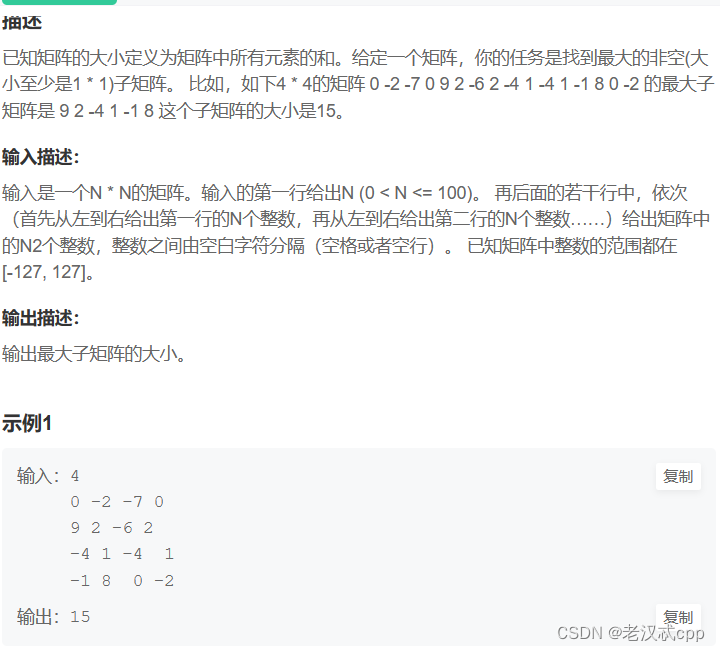
这是一道二维的前缀和问题。
了解题意后，我们需要确定怎样枚举每一个子矩阵。
我们可以创建四层for循环，x1,y1,x2,y2，这样就能枚举到每一个子矩阵了。
然后，我们再创建一个二维的dp表，dp[i][j]表示从（0，0）到（i，j）的矩阵大小。那么首先先填dp表，dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1]。可以对照图
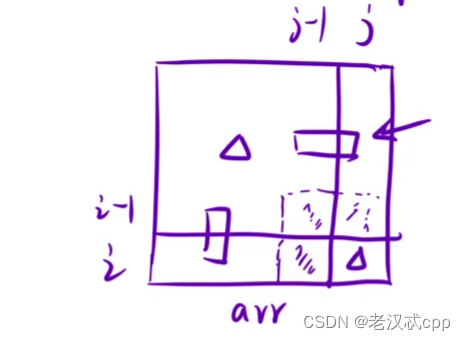
接着，枚举每一个子矩阵，就要用到这个dp表，
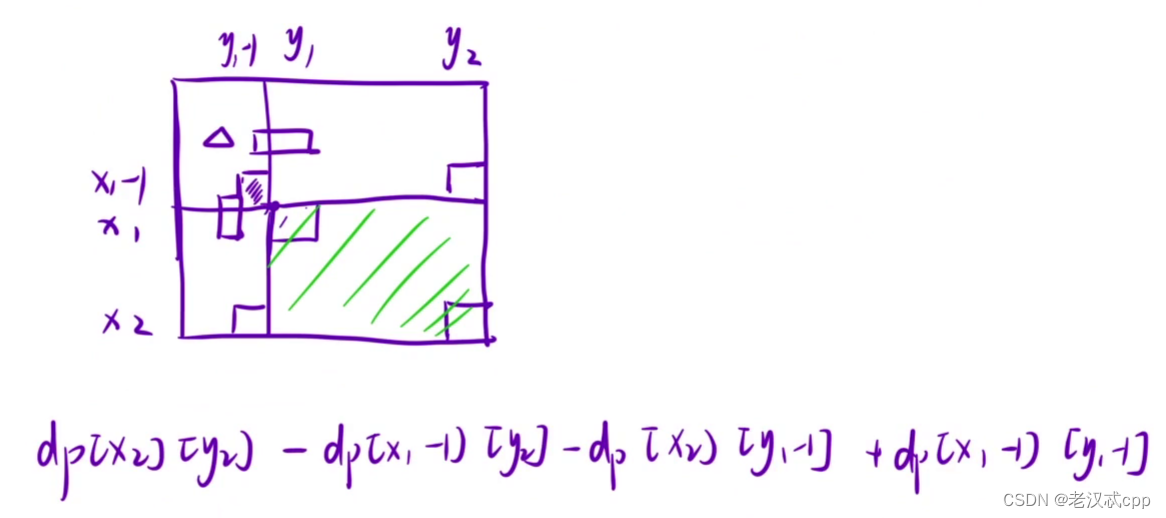每次枚举的结果就是 dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 - 1][y1 - 1]。每次记录最大值。
代码：
#include <iostream>
const int N = 110;
int n;
int dp[N][N] = {0};
using namespace std;
int main()
{
int x;
cin >> n;
for(int i = 1; i <= n; ++i)
{
for(int j = 1; j <= n; ++j)
{
cin >> x;
dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1] + x;
}
}
int ret = -127;
for(int x1 = 1; x1 <= n; ++ x1)
for(int y1 = 1; y1 <= n; ++y1)
for(int x2 = x1; x2 <= n; ++x2)
for(int y2 = y1; y2 <= n; ++y2)
ret = max(ret,dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 - 1][y1 - 1]);
cout << ret << endl;
return 0;
}
25.小葱的01串
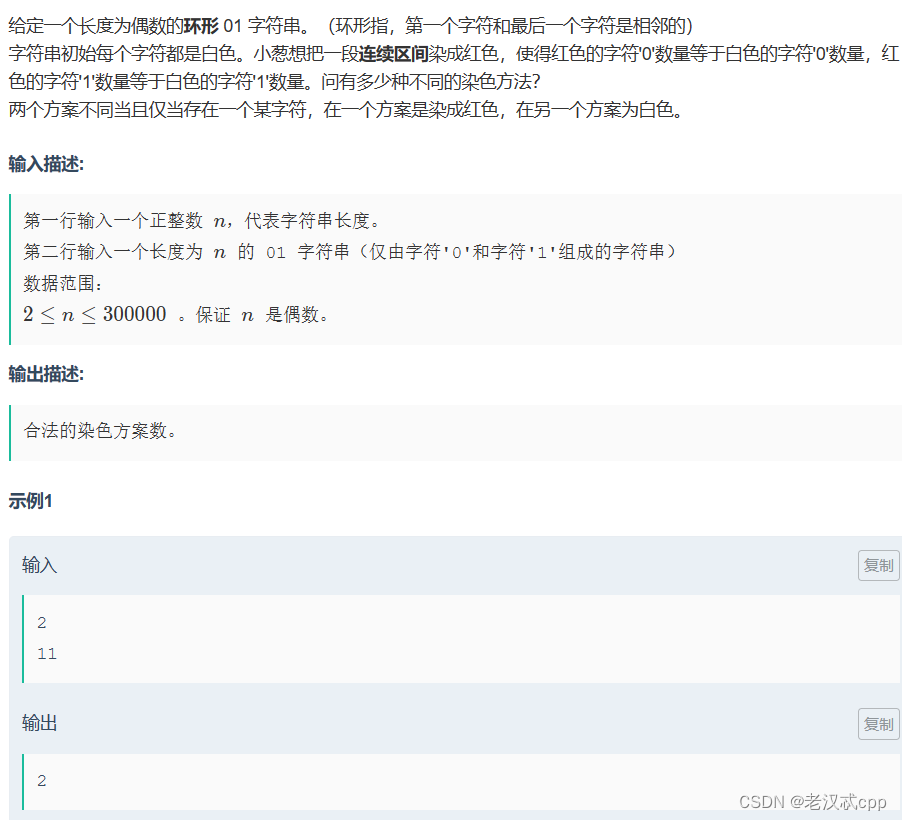
这道题的解法：滑动窗口。
但是我们在使用滑动窗口前，需要对问题进行刨析：
根据题意，是需要染成红色的1和染成红色的0的字符数量相等，同理，染成白色的1也要和染成白色的0字符数量相等，这才能算一种方案。
那么既然是数量要相等，不就是整个字符串中的1字符数量的一半和0字符数量的一半吗？
那么我们每次枚举只需要枚举n/2的长度大小的字符串即可，只要这个子字符串里的0和1的字符数量分别都等于整个字符串0和1的字符数量的一半就算一种方案。
但是题意又说了，这是一个环形字符串，但是这道题必须是环形字符串才有意义，那么环形就会有以下情况：
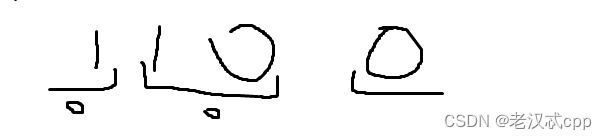
在图中，我们发现，枚举中间的10是一种方案，但是同时也会枚举出另一种方案，因此其实我们每次枚举的时候，就只要在一个完整的字符串内部枚举就可以了，不需要考虑环形的问题，每次枚举到一个方案时，再加1即可。也就是每次ret += 2。
分析到这里，就可以定义left，right开始使用滑动窗口了。
不过，在使用滑动窗口的时候，有一个细节问题，那就是right在循环的时候，它的条件是否可以是 while(right < n)呢？答案是不行的，会有以下这种情况
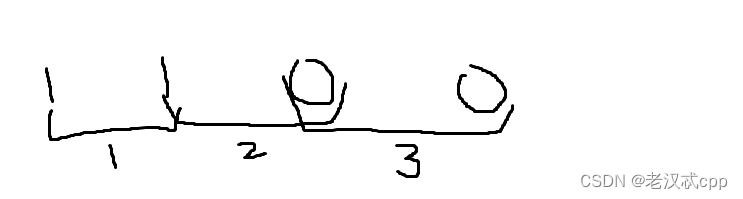如果字符串是1100这种情况的话，我们在枚举方案1的时候，其实已经把方案3考虑进去了，如果可以让right == n - 1的话，那么它又会枚举依次方案3，但是这样就重复了，使得结果会偏大而错误（多了2个方案）。因此，right的循环条件应该是 while(right < n - 1)。
代码：
#include <iostream>
using namespace std;
int main()
{
int n;
cin >> n;
string s;
cin >> s;
int zerocount = 0; // 0的所有数量
int onecount = 0; // 1的所有数量
for(int i = 0; i < n; ++i)
{
if(s[i] == '0') zerocount++;
else onecount++;
}
int left = 0;
int right = 0;
int ret = 0;
int num1 = 0; // 滑动窗口中0的数量
int num2 = 0;
while(right < n - 1) // 注意这里的细节
{
while(right < n - 1 && right - left < n / 2)
{
if(s[right] == '0')num1++;
else num2++;
right++;
}
if(num1 == zerocount / 2 && num2 == onecount / 2)
ret += 2;
if(s[left] == '0') num1--;
else num2--;
left++;
}
cout << ret << endl;
return 0;
}
26.分割等和子集
解法：动态规划。
算法流程：
状态表示：dp[i][j] 表示在前i个数据中，能否凑成j的值，因此dp表的类型是bool类型。
状态转移方程分析：对于第i个数据：
1.我们可以不选 -> dp[i - 1][j]。
2.我们选 -> dp[i - 1][j - arr[i]]，另外这里需要注意要判断j >= arr[i]，否则会越界。
那么 dp[i][j] = dp[i - 1][j] || dp[i - 1][j - arr[i]]。
初始化：
dp[0][0] = true。
返回值：
dp[n][sum / 2]。
另外在写代码前，还有一个细节，如果 sum % 2 == 1，说明无论我们怎么求，它都不能凑成sum的一半，所以要先判断，如果 sum % 2 == 1，那么直接输出false。
代码（未空间优化）
#include <iostream>
using namespace std;
bool dp[510][50000] = {0};
int arr[510] = {0};
int main()
{
int n;
cin >> n;
int sum = 0;
for(int i = 1; i <= n; ++i)
{
cin >> arr[i];
sum += arr[i];
}
if(sum % 2 == 1) cout << "false" << endl;
else
{
int ret = sum / 2;
dp[0][0] = true;
for(int i = 1; i <= n; ++i)
for(int j = 1; j <= ret; ++j)
{
if(j >= arr[i])
dp[i][j] = dp[i - 1][j] || dp[i - 1][j - arr[i]];
else
dp[i][j] = dp[i - 1][j];
}
if(dp[n][ret]) cout << "true" << endl;
else cout << "false" << endl;
}
return 0;
}
空间优化后：
#include <iostream>
using namespace std;
bool dp[50000] = {0};
int arr[510] = {0};
int main()
{
int n;
cin >> n;
int sum = 0;
for(int i = 1; i <= n; ++i)
{
cin >> arr[i];
sum += arr[i];
}
if(sum % 2 == 1) cout << "false" << endl;
else
{
int ret = sum / 2;
dp[0] = true;
for(int i = 1; i <= n; ++i)
for(int j = ret; j >= arr[i]; --j)
dp[j] = dp[j - arr[i]];
if(dp[ret]) cout << "true" << endl;
else cout << "false" << endl;
}
return 0;
}
27.不相邻取数
解法：动态规划
算法流程：
这是一道很简单的线性dp问题。
状态表示：有两个：
1.dp[i][0] 表示以i位置为结尾，不选择i位置的值的最大值。
2.dp[i][1] 表示以i位置为结尾，选择i位置的值的最大值。
状态转移方程：
1.dp[i][0] = arr[i] + dp[i - 1][1]
2.dp[i][1] = max(dp[i - 1][0],dp[i - 1][1])
初始化：
dp表中默认都为零就行
返回值：
两个表中的最大值
代码：
#include <iostream>
#include <vector>
using namespace std;
int main()
{
int n;
cin >> n;
vector<vector<int>> dp(n + 1,vector<int>(2)); // 0是代表选i，1代表不选i
vector<int> nums(n + 1);
for(int i = 1; i <= n; ++i)
cin >> nums[i];
for(int i = 1; i <= n ;++i)
{
dp[i][0] = nums[i] + dp[i - 1][1];
dp[i][1] = max(dp[i - 1][1],dp[i - 1][0]);
}
cout << (max(dp[n][0],dp[n][1])) << endl;
return 0;
}
28.空调遥控
解法一：暴力解法
直接从[min,max]这个区间里面枚举温度，取最大值。
但是时间复杂度为O（N^2），大概率超时。但是我们可以从中优化，因此诞生解法二
解法二：排序加 二分查找
在枚举这一步我们是没法优化的，但是在查找的时候是可以优化，在排序后，我们依然枚举温度，不过我们只需要通过二分法找到在这个温度下，忍耐值最小的下标left，和忍耐值最大的下标right，将它们right - left + 1就是本次枚举的结果。简而言之就是每次枚举的温度t，看看数组中有多少个数是在[t - p,t + p]之间的即可。
它的时间复杂度是 O（logn * n），虽然不是本题的最优解，但是具有参考价值，但是这道题它允许有重复值，如果我们要查找t - p的下标，若是有多个 t - p，那么我们要找到最左边的 t - p的下标；如果我们要找t + p的下标，那么我们需要找到到最右边的 t + p的下标。这样的话设置二分查找的代码比较麻烦，知道有这个思路就行了。
解法三：排序 + 滑动窗口
同样是先排序，left表示窗口的最小值的下标，right表示窗口最大值的下标，只要max - min <= 2 * p即可，取整个过程中，滑动窗口的最大值。
因为要排序，所以这个解法的时间复杂度还是O(logn * n)，但是解法三还是快一些，并且代码好写。
代码：
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int main()
{
int n,p;
cin >> n >> p;
vector<int> arr(n);
for(int i = 0; i < n; ++i)
{
cin >> arr[i];
}
sort(arr.begin(),arr.end());
int left,right;
int ret = 1;
left = 0,right = 0;
while(right < n)
{
while(right < n && arr[right] - arr[left] <= 2 * p)
right++;
ret = max(ret,right - left);
while(left < right && arr[right] - arr[left] > 2 * p)
left++;
}
cout << ret << endl;
return 0;
}
29.kotori和气球
这道题非常简单，就是简单的数学问题（排列组合）
题意简单来说就是有n种球，数量不限，要将它们排成m个，但是相邻的球不能相同。
假如m = 3，除了第一个位置有n种选择，其余的位置都可以选择 n - 1种，那么只要一个循环就可以解决问题了
代码：
#include <iostream>
using namespace std;
int main()
{
int n,m;
cin >> n >> m;
int ret = n;
for(int i = 1; i < m; ++i)
{
ret *= (n - 1);
ret %= 109;
}
cout << ret << endl;
return 0;
}
30.走迷宫
这是一道简单的搜索问题，并且因为是要计算最少的移动次数，所以采用bfs（宽度优先搜索）
它的算法原理很简单，但是对代码能力有点要求。
其中需要注意的是，我们定义了一个 int dist[N][N]来表示这个点是否访问过，因为不能重复访问。但是我们将类型设置称为int，如果值是-1，则说明该点没有访问过，如果不是-1，说明是牛牛走到这个点所移动的次数。
还需要注意dist初始化，我们需要将dist[x1][y1] = 0。
另外，这道题的下标映射都是从1开始的，所以我们在接收输入用例的时候就可以从1开始填。
代码：
#include <cstring>
#include <iostream>
#include <queue>
using namespace std;
const int N = 1010;
char nums[N][N];
int dist[N][N];
int dx[4] = {0,0,1,-1};
int dy[4] = {1,-1,0,0};
int x1,y1,x2,y2;
int n,m;
int bfs()
{
if(nums[x2][y2] == '*') return -1;
queue<pair<int,int>> q;
q.push({x1,y1});
memset(dist, -1, sizeof(dist));
dist[x1][y1] = 0;
while(q.size())
{
auto [a,b] = q.front();
q.pop();
for(int i = 0; i < 4; ++i)
{
int x = a + dx[i];
int y = b + dy[i];
if(x >= 1 && x <= n && y >= 1 && y <= m && dist[x][y] == -1 && nums[x][y] != '*')
{
dist[x][y] = dist[a][b] + 1;
if(x == x2 && y == y2)
{
return dist[x][y];
}
q.push({x,y});
}
}
}
return -1;
}
int main()
{
cin >> n >> m;
cin >> x1 >> y1 >> x2 >> y2;
for(int i = 1; i <= n; ++i)
for(int j = 1; j <= m; ++j)
cin >> nums[i][j];
cout << bfs() << endl;
return 0;
}
31.主持人调度（二）
这道题难度偏高，先暴力枚举，再想办法从中优化。
首先还是需要将这些区间按照左端点从小到大进行排序。
暴力枚举：
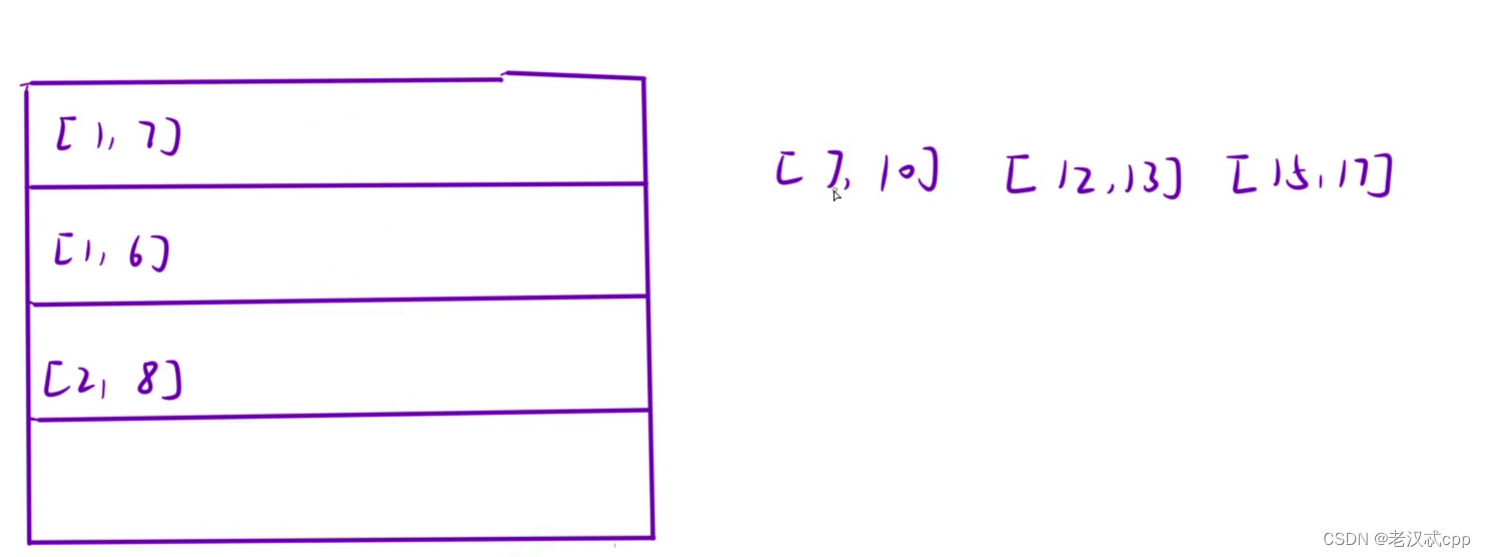
我们可以开辟一个二维数组，每一行表示可以用一个主持人搞定的节目，有几行就说明需要几个主持人。
这样的话时间复杂度是O(N^2)，依照题中的数据量是会超时的。那么接着来优化：
我们判断是否要增加主持人的依据是，以此遍历这个数组，如果s[i][0]小于每一行最后一个数的右端点的值话，就说明需要加一行了（也就是加一个人），否则就可以将它放到某一行的末尾。
那么其实每一行只需要放一个区间就够了，其次，我们每一行只需要保存右端点即可，左端点是用不到的。
然后，我们可以将剩余每一行的右端点放到一个小根堆中，如果此时来了一个数，它的左端点如果小于堆顶的元素（此时堆顶放的是右端点的值），那么它一定会冲突，此时就需要加一个人。
如果它的左端点大于等于堆顶的元素，说明这个区间的右端点可以替换某一行中的右端点。此时就pop掉堆顶的元素，将这个右端点的值push到堆中即可。
返回值就是返回堆的大小。
代码：
class Solution {
public:
int minmumNumberOfHost(int n, vector<vector<int> >& s) {
sort(s.begin(),s.end(),[](const vector<int>& v1,const vector<int>& v2){
return v1[0] < v2[0];
});
priority_queue<int,vector<int>,greater<int>> heap;
heap.push(s[0][1]);
for(int i = 1; i < n; ++i)
{
if(s[i][0] >= heap.top()) // 说明没有重叠，直接替换
{
heap.pop();
heap.push(s[i][1]);
}
else // 没有有重叠，需要再加一人
{
heap.push(s[i][1]);
}
}
return heap.size();
}
};
扫一扫
1260
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
