早点关注我,精彩不迷路!
在欧拉系列前面的文章中,我们已经从欧拉定理讲到了欧拉公式,相关内容请戳:
扒一扒那些叫欧拉的定理们(三)——简单多面体欧拉定理的抽象形式
扒一扒那些叫欧拉的定理们(一)——基本介绍和简单多面体欧拉定理
在上一篇中,我们从群论的观点给大家开了个头,介绍了直线上的两个变换群,分别对应正数乘法群和实数加法群,并指出了它们的同构关系,并且正是以指数函数作为映射函数。今天我们继续看,这些内容是怎么帮我们理解欧拉公式的。还是重复一下欧拉公式的内容:
e ^ ix = cosx + isinx,对任意复数x成立。
接着上一篇,我们提到在指数运算中,为了保持其乘法变加法的性质,从正整数扩展到0,负数,分数及全体实数的过程,而在欧拉公式中,竟然出现了虚数指数ix,故我们得继续把我们的数扩展到复数上,才能完全理解。那虚数指数幂的意义是什么呢,如何继续保持指数运算的性质呢?我们接着上篇的直线对称群继续看。
从直线对称群到平面对称群
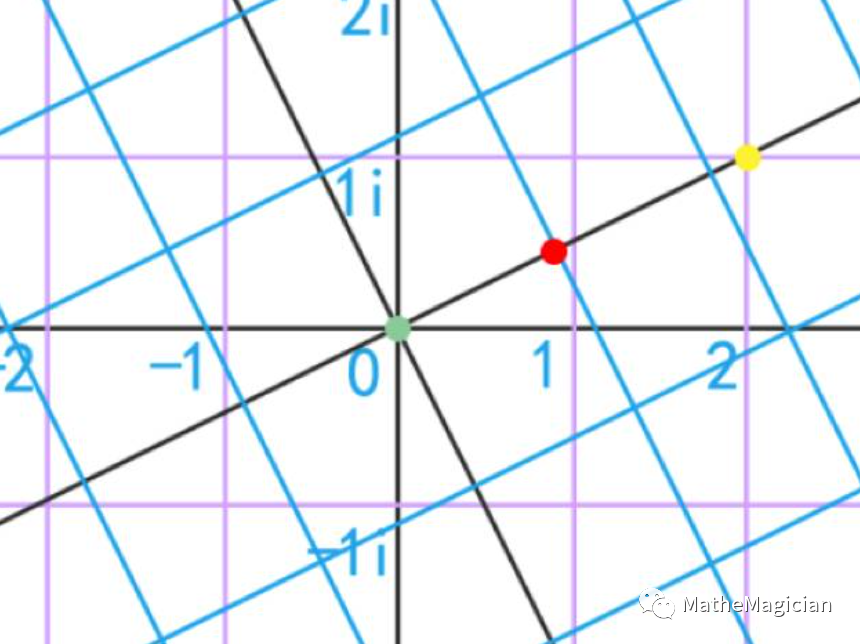
直线是个一维对象,很容易联想到对应的二维对象就是个平面。对应直线的左右平移,平面可以有左右和垂直的上下两个方向的运动保持其不变性,我们规定垂直方向的移动用i表示,那么a + bi就表示向右a个单位以及向上b个单位的整个平面的移动(负数时为左和下),此时将原平面的原点移动到点(a, b)上,也构造了移动这个操作和平面上的点对象的一一对应,这里看起来其实有点像向量表示的运动和其起点为原点时候的终点一一对应的意思了,这个群称为复数加法群(additive group of complex number),它比之前直线上的实数加法群多了一个方向的维度。
平移从一个方向变成两个方向,这是直线到平面的关于平移操作对称性维度扩展比较好理解的。但是拉伸和压缩呢?在新的平面上,我们仿照原来直线上坐标为1的点,以平面上的点(1, 0)作为基准,如果仅仅是拉伸压缩,(1, 0)只能在x轴上运动而已,只有水平方向拉伸压缩起作用,竖直方向的0不会动,并不能变换到平面上任意位置,于是这个基准点不行。一个直接的解决思路自然是把基准点改到(1, 1),那么由两个方向的拉伸压缩就可以将该点拉到第一象限的任意位置了。这样看起来就可以完成一个R ^ 2上的加法群和R+ ^ 2乘法群之间的同构了,也可以接着把指数运算的指数拓展为2维的,甚至更高维的向量,矩阵,张量,其结果只是平庸的各自元素对应运算结果在对应位置排列起来的结果罢了,平平无奇。
如果欧拉这么想就结束了的话,又怎么能证明他的伟大。假设我们仍然以(1, 0)为基点,保持直线的水平拉伸压缩变换,再加上一个什么变换,能够使得这个点可以变换到平面内任意位置呢?
答案是旋转!
没错,我们的平面明显对旋转也是对称的,而且,拉伸/压缩和旋转,可以使得基点抵达除原点以外的平面内所有点,这些点也和唯一的一个拉伸和2pi以内的旋转操作对应,甚至超出了原来第一象限的预期,这就把平面上的非原点和这两个操作合起来的复合元素一一对应起来了,重新构造了一个二维平面特色的复数乘法群(multiplicative group of complex numbers),整个二维平面只有远点不在其内,而拉伸/压缩,仅指水平方向。
接下来,我们仍然希望,这两个群之间,有同态关系,自然我们又找到了指数运算,并希望再度扩展其幂的取值为复数,即:
n ^ (a + bi) = n ^ a * n ^ bi
这里的复数可以理解为平面上的点,和复数加法群的操作一一对应。拆解出来的第一项是实数,刚好对应直线拉伸/压缩群(正实数乘法群)里的操作,而后一项,自然地就理解成旋转了。点(a, b)映射为点(n ^ a, b),由复数乘法的定义,对应点在原坐标下的坐标值为(n ^ a * cosb, n ^ a * sinb),这也是这两个群同构的一一映射的具体表达。大家应该也发现了,这就是我们极坐标系和直角坐标系的转换关系,本质上是两个平面复数群之间(复数加法群和非0复数乘法群)的同构关系表达式。
平面对称群与欧拉公式的关系
有了平面对称群的同构关系,这时候我们终于可以来理解一下虚数单位i以及欧拉公式的底为什么是自然对数的底e了。
一个显然的事实是,i这个值,对应的坐标是(0, 1),可以是0 + i得到,也可以是1 * i,为(1, 0)逆时针旋转90度的结果。我们希望(1 + 0i) * i = i = 0 + 1i,因此,*i必须是逆时针旋转90度的意思。所以i ^ 2 = - 1,表达的意思是,(1, 0)逆时针旋转两个90度以后到达(- 1, 0),用复数加法群的点表示法的完整表示是:(1 + 0i)* i * i = - 1 + 0i,这个理解是我们之前学的i是- 1的平方根更为本质的理解。
这里,n其实取任意正实数都能够完成这两个群结构的同态,但是我们欧拉公式中的e有什么特殊之处吗?这时候,我们回一下定义e的微分方程,有:
d(e ^ it) / dt = i * e ^ it
这个式子得到的思路同样是,我们在实数指数时候证明过指数求导公式以及复合公式,现在我们希望拓展到复数也成立。好了,现在假设成立了,我们来看看其物理意义,左边是e ^ it形式运动的速度,等于其位置乘以i,那不刚好就是逆时针旋转90度的意思吗?因此,其在平面内的运动轨迹满足:dy / dx * y / x = -1,起点为(1, 0),这时候,这不就是个单位圆吗?而且,也只有底数为e的时候,才能像公式里一样其在单位圆上的线速度刚好就是圆半径1,否则根据求导法则,系数提前以后还会要加速或者减速。
因此,在这时候,欧拉恒等式e ^ pi = - 1的运动意义是说,在复数乘法群的原点(1, 0)在单位圆上经过pi弧度的旋转以后,会到达(- 1, 0);而欧拉定理e ^ ix = cosx + isinx的意思是说,复数乘法群原点(1, 0)在单位圆上逆时针旋转x弧度以后,对应的点的坐标为(cosx, sinx)。用e作为底恰好使得等式两边的系数是1,可以省略,仅此而已。
看上去,这不几乎是显然的结论么,学习极坐标和直角坐标关系的时候不也学过了么,为啥要绕这么大一圈呢?没错,为了让指数函数运算以及求导的性质得以保持,发现只有底数为e的时候刚刚好,只是为了凑这个结论的形式才选了e,换别的数也行,只不过式子写起来不漂亮了。
看到了吧,只要把来龙去脉的思路理清楚了,到证明结论的时候,反而是显然的了。当x真的取复数的时候,我们同样可以根据定义扩展的策略为那些形式得到证明。
注意,我们其实选择的,是把序数轴上长度为2pi的一段映射到了单位圆上,并且刚好e ^ x这个函数满足了要求,然后整个平面上y轴区间[- pi, pi]的区间就从复数加法群映射为了整个非零复数乘法群,甚至任意一个长度为2pi的区间都可以映射过去,但是反过来不成立,复数上他们的映射不再是双射,因此只能是同态而不在同构了。
最后我想说,所谓复数的乘法群,无非就是以原点为不动点的拉伸/压缩和旋转两个操作下的平面对称群,本质上也是正实数乘法群和一个mod 2pi的实数加法群的直积,完全可以写成一个元组的形式(那就直接对应我们的极坐标系),也完全可以直接以给定的公式去作两个群的同态映射。指数本身则是沿用了直线对称群上的实数加法群和正实数乘法群的映射,而i符号引入在加法群里就是元组的扩展写法,在乘法群里,则是以e ^ i这样的形式,而底数e刚好因为微分方程的物理意义使得推导成立,所谓* i就是逆时针旋转90度,也暗含了一个(0, 1)这个点到两个平面群内的映射,即从向上平移1个单位到逆时针旋转90度的映射的转换。
以上就是欧拉公式的全部内容,你学懂了吗?

我们是谁:
MatheMagician,中文“数学魔术师”,原指用数学设计魔术的魔术师和数学家。既取其用数学来变魔术的本义,也取像魔术一样玩数学的意思。文章内容涵盖互联网,计算机,统计,算法,NLP等前沿的数学及应用领域;也包括魔术思想,流程鉴赏等魔术内容;以及结合二者的数学魔术分享,还有一些思辨性的谈天说地的随笔。希望你能和我一起,既能感性思考又保持理性思维,享受人生乐趣。欢迎扫码关注和在文末或公众号留言与我交流!


扫描二维码
关注更多精彩
Si Stebbins Stack中的数学与魔术(十一)——《Woody on Stebbins》作品赏析

点击阅读原文,往期精彩不错过!




















 7065
7065











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








