BZOJ 题目解析-CSDN博客

bzoj 3144

先二分答案，然后就是求一些条件是否都可行。
首先一个人一定在第一次记录到最后一次记录的这段区间内出现。
然后每段区间可以两边扩展，如果一个人没有记录过那么他的区间是任意的。
那么可以把当前工作的人分成三类：在区间内的人，区间未开始的人，区间已经结束的人。
没记录过的人属于第二种。
首先如果一个时间有两个人记录的不一样，那么一定无解。
如果某个时刻必选的人数大于要求的人数那么无解。
把区间在这个点开始的人加入第一类。
如果总人数太少那么将一些人加入第二类。
如果总人数太多先去掉第三类人，再去掉第二类人。
把在这个区间结尾的人从第一类加入第三类。

#include <bits/stdc++.h>
using namespace std;
#define N 110000
int T,n,m;
int tim[N],pos[N],num[N];
int ql[N],qr[N],st[N],en[N],v[N],cl[N],cr[N];
int check(int p)
{
    for(int i=1;i<=n;i++)ql[i]=m,qr[i]=0;
    for(int i=1;i<=m;i++)v[i]=0,cl[i]=0,cr[i]=0;
    for(int i=1,t,x,y;i<=p;i++)
    {
        t=tim[i];x=pos[i];y=num[i];
        if(v[t]&&v[t]!=y)return 0;
        ql[x]=min(ql[x],t);qr[x]=max(qr[x],t);
        v[t]=y;
    }
    for(int i=1;i<=n;i++)
        if(qr[i])cl[ql[i]]++,cr[qr[i]]++;
    int sum=0,rem=n,pl=0,pr=0;
    for(int i=1;i<=m;i++)
        if(v[i])
        {
            sum+=cl[i];
            if(sum>v[i])return 0;
            while(cl[i]--){if(pl)pl--;else rem--;}
            while(sum+pl+pr<v[i])pl++,rem--;
            while(sum+pl+pr>v[i]){if(pr)pr--;else pl--;}
            sum-=cr[i];pr+=cr[i];
            if(rem<0)return 0;
        }
    return 1;
}
int main()
{
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d%d",&n,&m);
        for(int i=1;i<=m;i++)
            scanf("%d%d%d",&tim[i],&pos[i],&num[i]),num[i]++;
        int l=0,r=m;
        while(l<=r)
        {
            int mid=(l+r)>>1;
            if(check(mid))l=mid+1;
            else r=mid-1;
        }
        printf("%d\n",r);
    }
    return 0;
}

bzoj 3415

题意：n个点m条边无向图，每条边权值为a，在每对最短距离为2a的点间加权值为b的边。求点K到其他点的最短路。

出题人脑洞太大+暴力出奇迹。。。。
设K到点i的最短路为x，最短偶数长度的路径为y，答案可能为 $xa,x/2*b+x\%2*a,y/2*b$ 。
前两个bfs一遍就出来了。。
对于第三个，考虑暴力：每次找与当前点连边的所有点，再找与那些点连边的所有点。如果还没有被访问过那么标记并推入队列。
不过这个是 $m^2$ 的。
考虑从第一层的x找到第二层y后下一次再以x为第一层找第二层时不访问x到y的边。可以用双向边表维护第二层的边。
然后删掉的边是 $O(m)$ 的。复杂度等于未删的边的访问次数,只能在三角形中出现：
$\sum min(du[i]^2,m)\le\sum \sqrt{du[i]^2m}=\sum du[i]\sqrt{m}=O(m\sqrt{m})$

#include <bits/stdc++.h>
using namespace std;
#define N 210000
int n,m,a,b,K;
queue<int>q;
int ans[N],deep[N],vis[N];
struct edge
{
    int head[N],nex[N],to[N],pre[N],tot;
    void add(int x,int y)
    {
        tot++;
        nex[tot]=head[x];pre[head[x]]=tot;
        head[x]=tot;to[tot]=y;
    }
    void ade(int x,int y)
    {add(x,y);add(y,x);}
    void del(int x,int y)
    {
        if(y==head[x])head[x]=nex[y];
        else
        {
            nex[pre[y]]=nex[y];
            pre[nex[y]]=pre[y];
        }
    }
}e1,e2;
int main()
{
    //freopen("tt.in","r",stdin);
    scanf("%d%d%d%d%d",&n,&m,&K,&a,&b);
    for(int i=1,x,y;i<=m;i++)
    {
        scanf("%d%d",&x,&y);
        e1.ade(x,y);e2.ade(x,y);
    }
    q.push(K);deep[K]=1;
    while(!q.empty())
    {
        int x=q.front();q.pop();
        for(int i=e1.head[x],t;i;i=e1.nex[i])
            if(!deep[t=e1.to[i]])
            {
                deep[t]=deep[x]+1;
                q.push(t);
            }
    }
    for(int i=1,t;i<=n;i++)
    {
        t=deep[i]-1;deep[i]=0;
        ans[i]=min(t*a,(t>>1)*b+(t&1)*a);
    }
    q.push(K);deep[K]=1;
    while(!q.empty())
    {
        int x=q.front();q.pop();
        for(int i=e1.head[x];i;i=e1.nex[i])
            vis[e1.to[i]]=1;
        for(int i=e1.head[x],t1,t2;i;i=e1.nex[i])
        {
            for(int j=e2.head[t1=e1.to[i]];j;j=e2.nex[j])
                if(!deep[t2=e2.to[j]]&&!vis[t2])
                {
                    deep[t2]=deep[x]+1;
                    q.push(t2);
                    e2.del(t1,j);
                }
        }
        for(int i=e1.head[x];i;i=e1.nex[i])
            vis[e1.to[i]]=0;
    }
    for(int i=1;i<=n;i++)
        if(deep[i])
            ans[i]=min(ans[i],(deep[i]-1)*b);
    for(int i=1;i<=n;i++)
        printf("%d\n",ans[i]);
    return 0;
}

bzoj 3416

这个倒过来就相当于每次取一段连续的区间。这个只和中间的c是谁有关，和两边的b的取法无关。因此只需要每次找一个两边b个数大于等于k的c删掉，这个我用了两个双向链表维护。

#include <bits/stdc++.h>
using namespace std;
#define N 1100000
int n,m;
char s[N];
int n1[N],p1[N],n2[N],p2[N],L[N],R[N],vis[N];
queue<int>q;
vector<int>ans[N];
int main()
{
    //freopen("tt.in","r",stdin);
    scanf("%d%d",&n,&m);
    scanf("%s",s+1);
    for(int i=0;i<=n;i++)
        n1[i]=i+1,p1[i]=i-1;
    int now=n+1;
    for(int i=n;i>=1;i--)
        if(s[i]=='c')
            n2[i]=now,p2[now]=i,now=i;
    n2[0]=now;
    for(int i=n2[0];i<=n;i=n2[i])
    {
        L[i]=i-p2[i]-1,R[i]=n2[i]-i-1;
        if(L[i]+R[i]>=m)q.push(i);
    }
    for(int now=1;now<=n/(m+1);now++)
    {
        int t=q.front();
        for(;L[t]+R[t]<m||vis[t];t=q.front())q.pop();
        vis[t]=1;
        R[p2[t]]=L[n2[t]]=L[t]+R[t]-m;
        if(p2[t]&&L[p2[t]]+R[p2[t]]>=m)q.push(p2[t]);
        if(n2[t]<=n&&L[n2[t]]+R[n2[t]]>=m)q.push(n2[t]);
        p2[n2[t]]=p2[t];n2[p2[t]]=n2[t];

        int ln=min(L[t],m),rn=m-ln,lp=p1[t],rp=n1[t];
        for(int i=1;i<=ln;i++)lp=p1[lp];
        for(int i=1;i<=rn;i++)rp=n1[rp];
        for(int i=n1[lp];i!=rp;i=n1[i])
            ans[now].push_back(i);
        n1[lp]=rp;p1[rp]=lp;    
    }
    for(int now=n/(m+1);now>=1;now--)
    {
        for(int j=0;j<m;j++)
            printf("%d ",ans[now][j]);
        printf("%d\n",ans[now][m]);
    }
    return 0;
}

bzoj 3147

首先如果存在长度为 $d(d>0)$ 的路径，一定存在长度为 $d+2k$ 的路径。因为可以在一条边上摩擦。
因此只需要处理两点之间长度为奇数和偶数的最短路就可以了。
把询问离线，从每个点出发跑分层图spfa。
由于边权都为1因此也可以bfs。

#include <bits/stdc++.h>
using namespace std;
#define N 5100
#define M 1100000
struct node{int x,d,pos;};
vector<node>v[N];
int n,m,K,tot;
int head[N],nex[N<<1],to[N<<1];
int f[N][2],inq[N],ans[M];
queue<int>q;
void add(int x,int y)
{
    tot++;
    nex[tot]=head[x];head[x]=tot;
    to[tot]=y;
}
int main()
{
    scanf("%d%d%d",&n,&m,&K);
    for(int i=1,x,y;i<=m;i++)
    {
        scanf("%d%d",&x,&y);
        add(x,y);add(y,x);
    }
    for(int i=1,x,y,d;i<=K;i++)
    {
        scanf("%d%d%d",&x,&y,&d);
        v[x].push_back((node){y,d,i});
    }
    for(int now=1;now<=n;now++)
    {
        memset(f,0x3f,sizeof(f));
        for(int i=head[now];i;i=nex[i])
        {
            f[to[i]][1]=1;inq[to[i]]=1;
            q.push(to[i]);
        }
        while(!q.empty())
        {
            int tmp=q.front();q.pop();
            inq[tmp]=0;
            for(int i=head[tmp];i;i=nex[i])
            {   
                int flag=0;
                for(int j=0;j<=1;j++)
                    if(f[to[i]][j]>f[tmp][j^1]+1)       
                        f[to[i]][j]=f[tmp][j^1]+1,flag=1;
                if(flag&&!inq[to[i]])
                    inq[to[i]]=1,q.push(to[i]);
            }
        }
        for(int i=0;i<v[now].size();i++)
        {
            node t=v[now][i];
            ans[t.pos]=(f[t.x][t.d&1]<=t.d);
        }
    }
    for(int i=1;i<=K;i++)
        puts(ans[i] ? "TAK":"NIE");
    return 0;
}

bzoj 3418

找出每一段连续的未被照亮的区间，设左右端点为L,R。那么光源一定在直线L,R上。
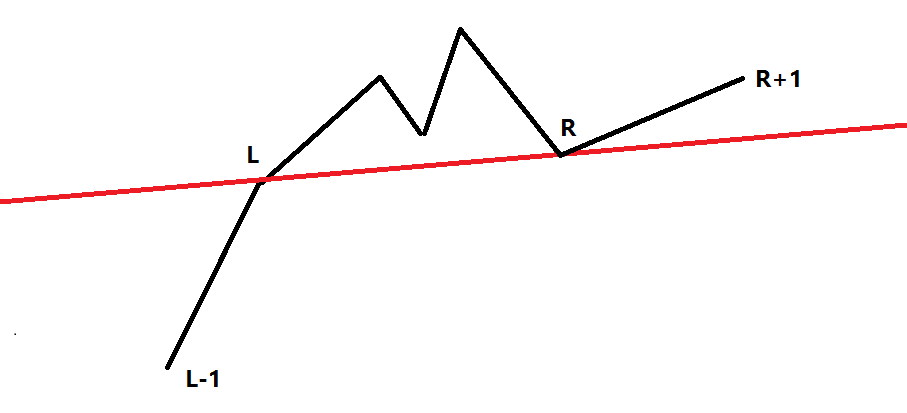
这里写图片描述
如果L-1,R+1在直线L,R的同侧那么一定无解。
如果L,R之间的部分和直线L,R有交点，无解。
如果L,R之间的部分在直线L,R右侧，无解。

如果有未被照亮的区间：解一定在所有直线L,R的交集中，为一条直线或一个点。如果所有L,R不交于一个点那么无解。
对于其他被照亮的线段，每条线段给当前解的直线或线段确定一个左端点或右端点。同时判断一下无解的情况。
这里写图片描述

如果没有未被照亮的区间：如果最后有解那么解一定是一些边所在的直线交出来的一个面。那么可以理解为最后解在其中一条边所在的直线上。同上述做法，其他每条边给当前解确定一个左右端点。

#include <bits/stdc++.h>
using namespace std;
#define ld long double
#define N 1100
const ld inf=1e9;
int T,n,cnt;
char s[11];
int val[N<<1];
ld read(){int x;scanf("%d",&x);return (ld)x;}
struct poi
{
    ld x,y;
    poi(){}
    poi(ld x,ld y):x(x),y(y){}
    friend poi operator - (const poi &r1,const poi &r2)
    {return poi(r1.x-r2.x,r1.y-r2.y);};
    friend ld operator ^ (const poi &r1,const poi &r2)
    {return r1.x*r2.y-r2.x*r1.y;};
    friend bool operator != (const poi &r1,const poi &r2)
    {return r1.x!=r2.x||r1.y!=r2.y;};
}p[N<<1],a[N],b[N];
struct line
{
    poi p,v;
    line(){}
    line(poi p,poi v):p(p),v(v){}
};
int turn(poi p1,poi p2,poi p3)
{return ((p2-p1)^(p3-p2))>0;}
int onleft(line l1,poi p1)
{return (l1.v^(p1-l1.p))>0;}
int ins_seg(poi p1,poi p2,poi p3,poi p4)
{
    line l1(p1,p1-p2),l2(p3,p3-p4);
    return (onleft(l1,p3)^onleft(l1,p4))&&(onleft(l2,p1)^onleft(l2,p2));
}
ld ins_line(poi p1,poi p2,poi p3,poi p4)
{return ((p4-p3)^(p1-p3))/((p1-p2)^(p3-p4));}
int check(poi p1,poi p2)
{
    ld l=-inf,r=inf;int flag=0;
    for(int i=1;i<=cnt;i++)
    {
        if(((p2-p1)^(b[i]-a[i]))==0)
        {
            if(p1!=a[i]&&p2!=b[i])return 0;
        }
        else
        {
            ld x=ins_line(p1,p2,a[i],b[i]);
            if(l!=-inf&&l!=x)return 0;
            l=r=x;flag=1;
        }
    }
    for(int i=1;i<=n;i++)
        if(val[i])
        {
            if(((p2-p1)^(p[i]-p[i+1]))==0)
            {
                if(((p[i+1]-p[i])^(p1-p[i]))>0)
                    return 0;
            }
            else
            {
                ld x=ins_line(p1,p2,p[i],p[i+1]);
                if(flag&&(x==l))return 0;
                if(((p2-p1)^(p[i+1]-p[i]))>0)l=max(l,x);
                else r=min(r,x);
                if(!flag&&l==r)return 0;
                if(l>r)return 0;
            }
        }
    return 1;
}
int solve()
{
    int l=1,r,t;cnt=0;
    for(;!val[l]&&l<=n;l++);
    if(l>n)return 0;
    for(r=l,t=l;l<n+t;l=++r)
        if(!val[l])
        {
            for(;!val[r];r++);
            int t1=turn(p[l-1],p[l],p[r]),t2=turn(p[l],p[r],p[r+1]);
            if(t1==t2)return 0;
            for(int i=l+1;i<r-1;i++)
                if(ins_seg(p[i],p[i+1],p[l],p[r]))return 0;
            if(r>l+1&&t2&&turn(p[l],p[r],p[r-1])!=turn(p[l],p[r],p[r+1]))return 0;
            if(r>l+1&&t1&&turn(p[r],p[l],p[l-1])!=turn(p[r],p[l],p[l+1]))return 0;
            a[++cnt]=p[l];b[cnt]=p[r];
        }
    if(!cnt)
    {
        for(int i=1;i<=n;i++)
            if(check(p[i],p[i+1]))return 1;
        return 0;
    }
    return check(a[1],b[1]);
}
int main()
{
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d",&n);
        for(int i=1;i<=n;i++)
            p[i].x=read(),p[i].y=read();
        for(int i=1;i<=n;i++)
            scanf("%s",s),val[i]=(s[0]=='S');
        for(int i=1;i<=n;i++)p[i+n]=p[i],val[i+n]=val[i];
        p[0]=p[n];val[0]=val[n];
        p[n*2+1]=p[1];val[n*2+1]=val[1];
        puts(solve() ? "TAK":"NIE");
    }
    return 0;
}

bzoj 3419

如果 $m=d$ 的话每次选最长的贪心。这个东西推一下式子就行。
否则需要留出来一个最后一次走过去。

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define N 510000
ll m,d;
int n;
ll a[N];
int cmp(ll x,ll y){return x>y;}
int main()
{
    scanf("%lld%lld%d",&m,&d,&n);
    for(int i=1;i<=n;i++)scanf("%lld",&a[i]);
    sort(a+1,a+1+n,cmp);
    int pos=0;
    for(;a[pos+1]>=m-d&&pos<n;pos++);
    if(!pos)return puts("0"),0;
    ll sum=0;int ans=1;
    for(int i=1;i<=n;i++)
        if(i!=pos)
        {
            if(m-sum+d-sum<=a[pos])break;
            if(a[i]<(d-sum))return puts("0"),0;
            ans++;sum+=a[i]-(d-sum);
            if(sum>=d)break;
        }   
    if(m-sum+d-sum>a[pos])return puts("0"),0;
    printf("%d\n",sum>=m ? ans-1:ans);
    return 0;
}

bzoj 3420

二分答案。设 $f[i]$ 表示现在在点i，i及i的子树中需要的额外点数。
那么 $f[i]=(\sum f[son[i]]+1)-v$ ，v为现在二分的答案。

#include <bits/stdc++.h>
using namespace std;
#define N 310000
#define ll long long 
int n,tot,ans,v;
queue<int>q;
int head[N],nex[N<<1],to[N<<1];
ll f[N];
void add(int x,int y)
{
    tot++;
    nex[tot]=head[x];head[x]=tot;
    to[tot]=y;
}
void dfs(int x,int y)
{
    f[x]=0;
    ll cnt=0,sum=0;
    for(int i=head[x];i;i=nex[i])
        if(to[i]!=y)
        {
            dfs(to[i],x);
            cnt++;sum+=f[to[i]];
        }
    f[x]=max(sum+cnt-v,0ll);
}
int check(int x)
{
    v=x;dfs(1,0);
    return !f[1];
}
int main()
{
    scanf("%d",&n);
    if(n==1)return puts("0"),0;
    for(int i=1,x,y;i<n;i++)
    {
        scanf("%d%d",&x,&y);
        add(x,y);add(y,x);
    }
    int l=1,r=n;
    while(l<=r)
    {
        int mid=(l+r)>>1;
        if(check(mid))r=mid-1;
        else l=mid+1;
    }
    printf("%d\n",l);
    return 0;
}

bzoj 3421

辣鸡bz卡我常数毁我青春
有一个结论，如果两个点所在的块大小都大于n*k则两个点在一块内。
那么分别从两个点开始bfs，如果搜n*k步以内能搜到另一个点或块内都有大于等于n*k个点那么有解。

#include <bits/stdc++.h>
using namespace std;
#define mod 9999991
#define N 5100000
#define M 11000000
#define ll long long 
int n,m,r1,r2,mx,tot;
int nex[N],head[M];
ll S,T,t;
ll q[N],val[N],a[1100000],bir[62];
void ins1(ll x)
{
    int t=x%mod;
    val[++tot]=x;
    nex[tot]=head[t];head[t]=tot;
}
void ins2(ll x)
{
    int t=x%mod;
    for(int i=head[t];i;i=nex[i])
        if(val[i]==x)return;
    val[++tot]=x;
    nex[tot]=head[t];head[t]=tot;
    q[++r1]=x;
}
ll trs()
{
    ll ret=0;
    char c=getchar();
    for(;c!='0'&&c!='1';c=getchar());
    for(int i=1;i<=n;i++)
        ret=(ret<<1)+(c=='1'),c=getchar();
    return ret;
}
int main()
{
    scanf("%d%d",&n,&m);
    S=trs();T=trs();mx=n*m;
    int i,j;
    bir[0]=1;
    for(i=1;i<=n;i++)
        bir[i]=bir[i-1]<<1;
    for(i=1;i<=m;i++)
        a[i]=trs(),ins1(a[i]);

    q[r1=1]=S;ins2(S);
    for(i=1;i<=r1&&r1<=mx+1;i++)
    {
        t=q[i];
        if(t==T)return puts("TAK"),0;
        for(j=0;j<n;j++)
            ins2(t^bir[j]);
    }
    if(r1<=mx)return puts("NIE"),0;
    memset(head,0,sizeof(head));tot=0;
    for(i=1;i<=m;i++)ins1(a[i]);

    r2=r1;q[r1=1]=T;ins2(T);
    for(i=1;i<=r1&&r1<=mx+1;i++)
    {
        t=q[i];
        if(t==S)return puts("TAK"),0;
        for(j=0;j<n;j++)
            ins2(t^bir[j]);
    }
    return puts(r1>mx&&r2>mx ? "TAK":"NIE"),0;
}