剑指offer-63:数据流中的中位数
目录
1题目描述
如何得到一个数据流中的中位数?
如果从数据流中读出奇数个数值,那么中位数就是所有数值排序之后位于中间的数值。
如果从数据流中读出偶数个数值,那么中位数就是所有数值排序之后中间两个数的平均值。
2队列和优先队列

例子:
#include <iostream>
#include <queue>
using namespace std;
int main(){
queue<int> q;
q.push(4);
q.push(5);
cout<<q.front()<<endl;
q.pop();
}运行结果:
4

优先级队列可以用向量(vector)或双向队列(deque)来实现
(注意list container 不能用来实现queue,因为list 的迭代器不是任意存取iterator,而pop 中用到堆排序时是要求randomaccess iterator 的!):
priority_queue<vector<int>, less<int>> pq1; // 使用递增less<int>函数对象排序
priority_queue<deque<int>, greater<int>> pq2; // 使用递减greater<int>函数对象排序其成员函数有“判空(empty)” 、“尺寸(Size)” 、“栈顶元素(top)” 、“压栈(push)” 、“弹栈(pop)”等。
例子:
#include <iostream>
#include <queue>
using namespace std;
class T {
public:
int x, y, z;
T(int a, int b, int c):x(a), y(b), z(c){ }
};
bool operator < (const T &t1, const T &t2) {
return t1.z < t2.z; // 按照z的顺序来决定t1和t2的顺序
}
int main(){
priority_queue<T> q;
q.push(T(4,4,3));
q.push(T(2,2,5));
q.push(T(1,5,4));
q.push(T(3,3,6));
while (!q.empty()) {
T t = q.top();
q.pop();
cout << t.x << " " << t.y << " " << t.z << endl;
}
}3 3 6
2 2 5
1 5 4
4 4 3
#include <iostream>
#include <queue>
using namespace std;
class T {
public:
int x, y, z;
T(int a, int b, int c):x(a), y(b), z(c){ }
};
bool operator > (const T &t1, const T &t2) {
return t1.z > t2.z; // 按照z的顺序来决定t1和t2的顺序
}
int main(){
priority_queue<T, vector<T>, greater<T> > q;
q.push(T(4,4,3));
q.push(T(2,2,5));
q.push(T(1,5,4));
q.push(T(3,3,6));
while (!q.empty()) {
T t = q.top();
q.pop();
cout << t.x << " " << t.y << " " << t.z << endl;
}
}4 4 3
1 5 4
2 2 5
3 3 6
如果我们把第一个例子中的比较运算符重载为:
bool operator < (const T &t1, const T &t2) {
return t1.z > t2.z; // 按照z的顺序来决定t1和t2的顺序
}则第一个例子的程序会得到和第二个例子的程序相同的输出结果。
3题目解析及答案
做法就是用一个大顶堆和一个小顶堆,维持大顶堆的数都小于等于小顶堆的数,且两者的个数相等或差1。
平均数就在两个堆顶的数之中。
class Solution {
priority_queue<int, vector<int>, less<int> > p; //最高优先级是最大的,依次top出递减,
priority_queue<int, vector<int>, greater<int> > q; //最高优先级是最小的,依次top出递增,
public:
void Insert(int num){
if(p.empty() || num <= p.top())
p.push(num); //在尾部加入一个元素
else
q.push(num);
if(p.size() == q.size() + 2) //p中元素个数,比q中元素个数,大1或相等
q.push(p.top()), p.pop(); //pop删除第一个元素不返回,
if(p.size() + 1 == q.size()) //如果p中元素比q少一个,将q的优先级元素给p
p.push(q.top()), q.pop(); //top返回最高优先级的元素
}
double GetMedian(){
return p.size() == q.size() ? (p.top() + q.top()) / 2.0 : p.top();
}
};









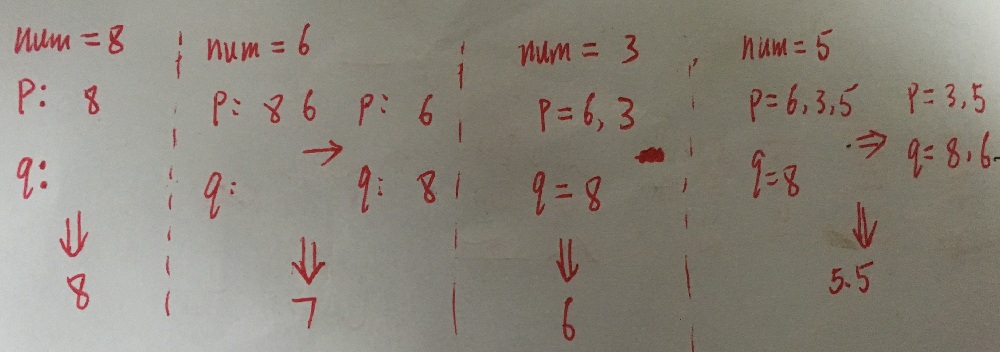













 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








