【论文】Efficient Label-Constrained Shortest Path Queries on Road Networks A Tree Decomposition Approach

ABSTRACT

  计算两个顶点之间的最短路径（the shortest path）是道路网络（Road Network）的一个的基本问题。已有的工作假设网络中的边是无标签，但现实中边是有标签的，标签约束（Label Constraint）可以放在有效最短路径（valid shortest path）的边上。因此(Hence)，本文研究了标签约束的最短路径查询。为了有效地处理这些查询，我们采用了一种基于索引的方法，并提出了一种基于树分解（Tree Decomposition）的新的索引结构—LSD-Index。利用LSD-Index，本文设计了一种具有良好性能保证（good performance guarantees）的高效查询处理算法。此外，本文还提出了一种构造LSD-Index的算法，并利用并行计算 （parallel computing）技术进一步提高了索引构建的效率。本文使用包括整个美国道路网在内的大型真实道路网进行了广泛的（extensive）性能研究。与目前最前沿的（state-of-the-art）方法相比，实验结果表明（demonstrate），我们的算法不仅在查询处理时间上实现了高达2个数量级（2 orders of magnitude）的加速，而且消耗了更少的索引空间。同时，索引时间也具有竞争力，特别是对于并行索引构造算法。

1 INTRODUCTION

  计算两个位置之间的最短路径是道路网络[3,8,9,12,14,20,22,28,30,34,40]中的基本问题之一。在真正的道路网中，并不是所有的道路都是一样的，例如，高速公路(highway)允许更快的通行，收费公路(toll road)需要付费，水源保护区内的道路禁止运输危险（hazardous）货物。因此，许多应用在计算最短路径时对出现在有效最短路径上的边进行约束，这导致了对标签约束最短路径查询（Label-Constrained Shortest Path Queries）[10,25]的研究。形式上，给定一个道路网络 G 每条边有一个标签，源顶点 s ，目标顶点 t ，和一个边标签集 $\mathcal{L}$ ，标签约束最短路径查询 q =(s,t,$\mathcal{L}$) 旨在计算从 s 到 t 的最短路径，最短路径的边标签包含在 $\mathcal{L}$ 。
  标签约束最短路径查询可以用于许多实际的应用场景，如个人常规规划[25]和紧急疏散导航(emergency evacuation navigation)[16]。例如，从Irvine, CA到Riverside, CA的最短路线沿着261号州公路行驶，这是一条穿过该地区的当地收费公路。用户不愿意支付收费费用，我们可以找到一条最短路径，实际上避免所有收费公路标签约束最短路径查询q=（“Irvine”，“Riverside”，$\mathcal{L}$），$\mathcal{L}$不包含带有（representing）收费标签的道路[25]。在中国，获得驾照不到12个月的新司机不得单独在高速公路上驾驶[31]。因此，在为这些新司机规划例程时，应避免使用高速公路，这可以通过标签约束最短路径查询来实现，其中$\mathcal{L}$不包含带有高速公路标签的道路。在紧急疏散导航中，建议的疏散路线应避开危险区域内的道路[16]，这可以通过标签约束最短路径查询来实现，其中$\mathcal{L}$不包含带有危险区域标签的道路。

Motivation

  标签约束最短路径查询的一种简单（straightforward）实现方法是使用Dijkstra算法[7]，在遍历过程中只访问边标签在$\mathcal{L}$中的边。虽然该方法可以计算出所需的最短路径，但由于道路网在实际应用中规模较大，因此当 s 和 t 距离很远时，它不能满足标签约束最短路径查询的实时性要求。因此，研究人员采用基于索引的技术来加速标签约束最短路径查询[10,25]。
  最先进的基于索引的方法是边不相交分区（Edge-Disjoint Partition）[10]。直观地说(Intuitively)，EDP是基于每个边标签对道路网络进行划分，并将每个分区中处理过的查询所计算出的最短路径信息缓存为索引结构。当一个新的查询出现时，缓存的信息将用于加快查询处理。显然，EDP的表现在很大程度上取决于该索引的命中率。然而，EDP的命中率并没有理论上的（theoretical）保证（guarantees），因为它只是在已处理的查询的每个分区中缓存计算的最短路径，但新提出的查询可能会处于不同分区，标签约束最短路径的特定查询可能涉及多个分区。因此（Consequently），很有可能一个特定查询的命中率很低，EDP退化（degenerate）为一个类似于直接使用Dijikstra算法的在线搜索算法。更糟糕的是，EDP的性能可能比直接使用Dijikstra算法要差，因为引入索引可能会访问更多的顶点。
  在此基础上，我们重新研究了道路网络上的标签约束最短路径查询，并旨在设计一种有效的具有理论性能保证的标签约束最短路径查询处理算法。

Our approach

  我们还采用基于索引的技术来完成有效的标签约束的最短路径查询处理。由于树分解可以将道路网络分解为深度小、宽度小的树状结构，在最近[15,21]计算无标记道路网络的最短路径方面取得了很大的成功。受此启发，我们重新讨论了基于树分解的最短路径问题的索引技术。
  我们从未标记的道路网络上的最短路径查询入手。关于这个问题，最先进的基于树分解的索引方法处理了一个时间复杂度为O（h·ω ²）的查询，其中h，ω分别（respectively）是树分解的树高，树宽[30]。通过仔细分析树分解的属性，我们提出了一个基于树分解算法的最短路径查询，和不平凡地证明算法的时间复杂度处理查询可以限制为O（h·ω），这减少了[30]ω的时间复杂度（参考定理4.13）。由于h和ω对于道路网络来说很小，这意味着我们可以在基于树分解的基础上有效地处理无标记道路网络上的最短路径查询，并具有理论上的性能保证。
  在此基础上，我们探索了基于树分解的标签约束最短路径查询的索引解决方案。一个直接索引解决方案如下：对于每个诱导道路网络的一个可能的边标签集Σ，集合Σ是给G中的边做标签的有限的字母表，我们把诱导道路网络作为一个未标记的道路网络，构建基于树分解索引。给定一个标签约束的最短路径q =（s，t，$\mathcal{L}$），我们检索边标签集$\mathcal{L}$对应的相应索引，并相应地计算最短路径。显然，这种方法用于无标记道路网络上的最短路径查询充分利用了基于树分解索引技术的高效性。然而，用这种方法构建的索引总数为2^|Σ|。构建和维护如此多的索引是被禁止的，这使得这种方法无法在实际应用中处理大型道路网络。
  观察直接解中构造的索引，我们发现在不同的索引之间存储了大量关于标签约束最短路径计算的冗余（redundant）信息。我们设想减少这2^|Σ|冗余信息，将它们整合成整体紧凑（holistic compact）的索引结构.为了使我们的想法适用实际，需要解决以下问题：

• (1)如何设计这样一个在减少冗余信息的同时不影响查询处理效率的索引？
• (2)如何有效地构建路网的索引，特别是在路网较大的情况下？

Contribution

  在本文中，我们讨论了上述问题，并作出了以下贡献：

1. 对无标记道路网络上的最短路径查询处理的一个新的更严苛的边界。我们重新讨论了基于树分解的无标记道路网络上最短路径查询的索引问题，并提出了解决该问题的一种算法。我们证明了新算法的时间复杂度为O（h·ω），而最先进的基于树分解的索引方法是O（h·ω ²）。
2. 具有理论性能保证的标签约束最短路径查询的高效算法。针对标签约束的最短路径查询，设计了一种新的基于树分解的索引。在此基础上，我们提出了一种回答查询的算法。我们还设计了一个算法来构造索引。此外，考虑到道路网络在实际应用中可能非常大，我们利用并行计算技术来进一步加快索引的构建。
3. 对真实道路网络的广泛性能研究。我们对包括美国整个路网在内的8个真实的大型公路网进行了广泛的性能研究。实验结果表明了该索引效率与效果并重。
     由于空间有限，本文省略了证据和部分实验结果，它们可以在我们的技术报告[39]中找到。

2 PRELIMINARIES

  设G =（V，E，ϕ，ℓ，Σ）是一个带标签的道路网，其中V (G)是一个顶点集，E (G)是一个边集合，ϕ： E (G)→R+是一个函数，它给每个边 e ∈E(G)分配一个正数ϕ（e,G）作为其权重，Σ是一个有限字母表，ℓ：E(G)→Σ是一个函数，分配每个边e∈E (G)一个标签ℓ（E,G）∈Σ。我们使用n=|V(G)|(m = |E (G)|)表示在G中的顶点数（边）。对于每个顶点v∈V (G)，v的邻居，用nbr(v,G)表示，被定义为nbr(v,G)= {u|(u,v)∈E(G)}。顶点v的度是v的邻居的数量。给标签Σ_s⊆Σ的一个子集，即G的Σ_s诱导子图，用G[Σ_s]表示，是包含G中所有边和Σ_s中标签的所有边的子图。G中的路径p是一个顶点序列 p =(v₀,v₁,v₂…v_k)，其中(v_i ,v_i+1) ∈ E (G)且所有i满足0≤i≤k−1。我们使用P(s,t,G)来表示从s到t的所有路径。路径的权重，用ϕ（p,G）表示，ϕ(p,G)=
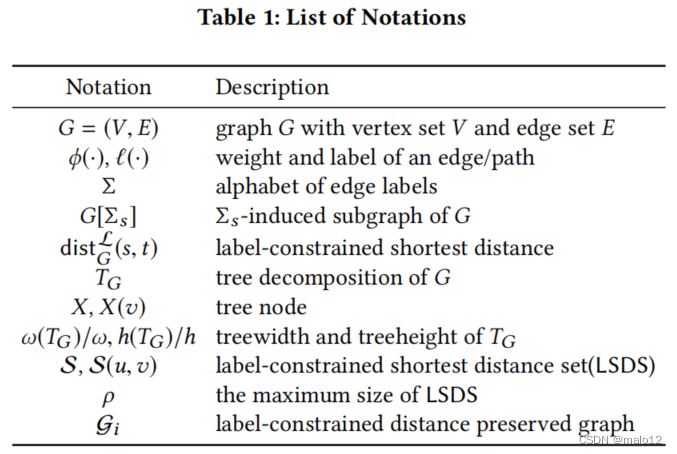
Σ_{0≤i≤k−1}ϕ(v_i,v_i+1)。给定两个顶点s和t，从s到t的最短路径是P(s,t,G)中权重最小的路径。最短距离，用dist_G(s,t)表示，是s和t之间的最短路径的权值。对于G中给定的路径p，p的标签用 ℓ (p,G)表示，是p的边标签的并集，例如，ℓ (p,G)* =U_e∈p ℓ (e,G)。为简单起见，如果上下文是不言而喻的，那么我们将在符号中省略G。为了便于参考，我们总结了表1中经常使用的符号。

  定义2.1 (Label-Constrained Path) 给定道路网络G =(V,E,ϕ,ℓ,Σ)中的两个顶点s,t和一组边标签$\mathcal{L}$ ⊆ Σ，如果 ℓ (p) ⊆$\mathcal{L}$ ，从s到t的路径是关于$\mathcal{L}$ 的标签约束路径。
  定义2.2 (Label-Constrained Shortest Path) 给定道路网络G =(V,E,ϕ,ℓ,Σ)中的两个顶点s,t和一组边标签$\mathcal{L}$ ⊆ Σ，从s到t的标签约束最短路径是关于$\mathcal{L}$的从s到t的标签约束路径中权值最小的路径。

Problem statement

  给定一个道路网络G =(V,E,ϕ,ℓ,Σ)，标签约束最短路径查询为 q =(s,t,$\mathcal{L}$) ，s,t∈V(G)，$\mathcal{L}$⊆Σ，答案是关于$\mathcal{L}$的从s到t的标签约束最短路径。在本文中，我们的目标是开发有效的索引技术来有效地回答查询q。
  为了便于解释，我们首先认为 G 是无向的，并在第5.5节中讨论了如何处理有向道路网。

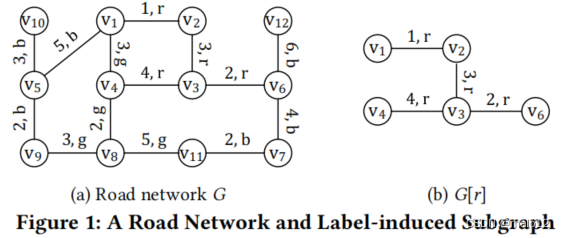
  例子2.3考虑图1 (a)中的路网G，每个边的权重和标签显示在对应的边旁。例如，ϕ((v₁,v₂))=1和ℓ((v₁,v₂))=r。对于一个边标签集{ r }，{ r }的诱导子图G[r]如图1(b)所示，它由带有r标签的边组成。给定顶点v₅、v₆和一个标签集{b,g}，在v₅和v₆之间有两条标签约束的路径：{(v₅,v₁,v₄,v₈,v₁₁,v₇,v₆), (v₅,v₉,v₈,v₁₁,v₇,v₆)},后一条是权重为16的标签约束最短路径。

3 EXISTING SOLUTION

  边缘不相交分区（EDP）[10]是针对受标签约束的最短路径查询的最新解决方案。EDP是一种基于索引的方法，由以下两个组成部分组成：
  EDP indexing 给定一个道路网络G，EDP首先通过边缘的标签来划分G。对于每个标签l∈Σ，分区Part_l包含带有标签l的边，也就是说， Part_l = G[l]。很明显，每条边标签唯一地对应于一个分区，当上下文是不言而喻的时，我们可以互换使用它们。基于分区，分区Part_li中如果存在一条边（v,u）∈Part_lj和l_i，l_j,则顶点v是一个桥顶点（Bridge Vertex）。对于桥顶点v∈Part_li，它的其他主机（OtherHosts）是包含v的其他分区。在处理查询时，它会计算每个分区中的最短路径。这些计算出的路径都被缓存在EDP索引中。随着处理更多的查询，导致索引大小超过指定的阈值，EDP使用最近使用最少的（LRU）替换策略，用新计算的最短路径替换旧路径。
  Query processing 对于查询q =（s，t，$\mathcal{L}$），EDP采用类似于Dijkstra算法的贪婪遍历范式来计算标签约束的最短路径。在遍历过程中，它维护一个最小优先级的队列Q，Q的每个元素都有三个属性：(1)Part：一个分区的标识符，(2) v：一个顶点id，(3) d：当前观察到的从s到v的距离。Q由（Part,v）键控，并由d排序。EDP最初将（Part_ls ,s,0）插入到Q中，其中Part_ls是s所在的分区。然后，EDP从Q中迭代提取元素们e’，展开遍历，并将发现的边界顶点插入到Q中，直到达到t或Q为空。在展开过程中，EDP首先计算从e’.v到 e’.Part 中的桥接顶点v’ 的最短距离d，然后，对于每个Part∈{$\mathcal{L}$’∩$\mathcal{L}$}，其中$\mathcal{L}$’表示e’.Part 中v’.OtherHosts 的标签。它将(Part,v’,d+e’.d)插入到Q(如果t在e’.Part中,t也适用于同样的处理)。当计算e’.v到桥顶点*v’*的距离时，如果发现其已经在索引中，EDP直接获得值；否则，执行Dijkstra算法并将结果缓存在索引中。
  Drawbacks of EDP EDP可以正确处理标签约束的最短路径查询，但在效率方面存在以下两个缺点：
    (1)理论上（theoretically），其查询处理时间不存在严格上下限。EDP的最坏情况下的时间复杂度并不比Dijkstra算法的在线搜索好。
    (2)实际上（practically），EDP只是缓存计算的最短路径在每个分区处理查询，但新发布的查询可能分布较散并且查询的最短路径可能涉及几个分区，很可能大部分的特殊查询所需的信息并不在缓存内。在这种情况下，EDP退化为一个基于在线遍历的算法，类似于Dijikstra的在线遍历算法。

4 A NAIVE INDEXING APPROACH

4.1 Tree Decomposition

  树分解[26]将图分解为树状结构，以加快图问题的解决，其定义为：
  定义4.1 (Tree Decomposition) 给定一个图G，G的树分解T_G是一个由节点{X₁，···，X_n}组成的有根树，其中每个节点是V (G)的子集（即X_i⊆V (G)）的子集，这样：
  (1) U_X∈V(TG)X = V (G);
  (2)对于每条边(u,v)∈E (G)，都有一个节点X∈T_G，使得u∈X和v∈X；
  (3)对于每个v∈V (G)，包含v (即{X|v∈X}) 的节点形成T_G的连通子树。
  定义4.2 (Treewidth and Treeheight) 给定一个G的树分解T_G，T_G的树宽表示为ω(T_G)，是T_G中所有节点的最大的大小-1，即ω(T_G) =max_X∈V(TG)|X| − 1。T_G的树高，用h(T_G)表示，是T_G中所有节点的最大深度（T_G中的某节点的深度是从该节点到T_G的根节点的距离）。
  为了便于表示，我们将G中的v∈V(G)称为一个顶点（vertex），而将T_G中的X∈V(T_G)称为一个节点（node）。如果上下文是不言而喻的，那么我们使用ω和h来表示树分解T_G的树宽和树高。图G的树宽是G所有可能的树分解的最小树宽。
  为了确定一个给定的图G是否有树宽，最多一个给定的变量是NP-完备的（NP-Complete）[2]。现有的计算最优树分解的技术只能处理小图[13]。因此，我们采用一种次优但实际上有效的算法MDE来进行树分解[35]。

Minimum degree elimination based tree decomposition

  MDE将树的分解分为两步进行：
    (1)迭代地(iteratively)消除G中度最小的顶点v，然后给v所有邻居之间添加边，在G中形成一个v邻居团。很明显，在消除v后，v的邻居成为它的邻居的邻居。它继续进行消除，直到G变为空。对于每一次消除，被消除的顶点v及其邻居nbr (v)在T_G中形成一个节点X (v)。
    (2)在消除了所有的顶点之后，对于每个节点X (v)，X (u)被设置为T_G中的X (v)的父节点，其中X(u)是由X (v){v}中的首先被消除的顶点u创建的节点。

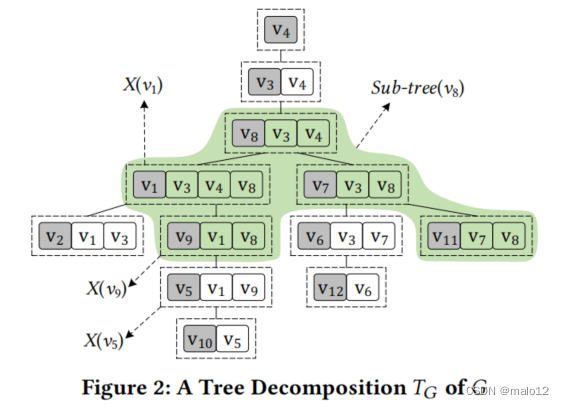
  例子 4.3 图2为MDE生成的图1 (a)中G的树状分解T_G。T_G有12个节点。顶点消除的顺序是v₁₀, v₁₂, v₅, v₂, v₆, v₁₁, v₇, v₉, v₁, v₈, v₃, v₄。一个顶点v的消除会在T_G中生成一个唯一的节点X (v) 。例如，v₅的消除将创建节点X(v₅)={v₅、v₁、v₉}。包含v₈的节点构成了T_G的连接子树（绿色区域）。由于T_G中的节点最多包含4个顶点，树宽为ω = 3，树高为h = 6。

4.2 A Naive Indexing Approach

  给定G =（V，E，ϕ，ℓ，Σ）有2^|Σ|个可能的边缘标签组合。因此，我们可以建立2^|Σ|个索引，每个索引通过Σ中的边标签的一个可能组合建立在诱导子图上。由于考虑了所有可能的边标签组合，对于每个索引，我们只需要将相应的诱导子图标记为无标记，并根据无标记道路网的最短路径索引技术建立索引。为了回答一个查询q =（s，t，$\mathcal{L}$），我们利用$\mathcal{L}$的索引来检索最短路径。根据这一想法，我们提出了一种基于树分解的朴素索引方法。
  在介绍简单的索引方法之前，我们首先介绍了树分解的顶点分割特性，该特性是将树分解应用于最短路径查询的关键。
  定义 4.4 (Vertex Cut) 给定一个图G，如果从G中删除C将G分割为多个连通分量，那么顶点的子集C⊂V(G)是G的顶点切割。
给定G中的两个顶点s和t，如果从G中删除C就断开了s和t，则顶点切割C是s-t切割，我们也可以说C分离s和t。
  引理 4.5 [27]给定一个G的树分解T_G，对于任何非根节点X_c及其父X_p，如果存在s∈X_c \X_p和t∈X_p\X_c，那么X_c∩X_p是G的一个顶点切割，并将s和t分开。
  引理 4.6 [5]给定一个G的树分解T_G，对于V(G)中任何两个顶点s和t，假设X (s)在T_G中不是X(t)的祖先，让X_lca在T_G中成为X(s)和X(t)的最近的共同祖先(the lowest common ancestor)（LCA），那么X_lca是G的一个顶点切割，分离s和t。
  给定一个s-t切割C，很明显，从s到t的每条路径都至少经过C中的一个顶点。因此，我们有：
  引理 4.7 [21]给定G中的两个顶点s和t，设C是一个s-t切割，则dist(s,t)=min_v∈C{dist(s,v)+dist(v,t)}。
  例 4.8 考虑图2中所示的G的树分解T_G。对于X(v9)及其父节点X(v1)，X(v₉)∩X(v₁)= {v₁,v₈}是G的一个顶点切割，它将v9和v3分开。如图2所示，对于X(v₁₀)和X(v₁₂)，它们的LCA为X(v₈)，不难得知dist(v₁₀,v₃) = 12, dist(v₁₀,v₄) = 10, dist(v₁₀,v₈) = 8; dist(v₁₂,v₃) = 8, dist(v₁₂,v₄) = 12 , dist(v₁₂,v₈) = 14, v₁₀到v₁₂的最短距离 = min(12 + 8, 10 + 12, 8 + 14) = 20.
  既然两个顶点之间的标签约束最短路径可以很容易地获得，如果用我们的算法确定了它们的标签约束最短距离，我们关注的是此后两个顶点之间标签约束的最短距离并讨论如何获得相应的最短5.4节中的路径。为了简洁起见，给定两个顶点u，v和一个边标签集$\mathcal{L}$⊆Σ，我们使用dist_G^L(u,v)来表示G中$\mathcal{L}$从u到从v的标签约束最短距离。

The naive indexing approach

基于上述引理，我们可以设计一种简单的索引方法来计算两个顶点之间的标签约束最短距离，如下：

• Indexing 对于每个可能的边标签集Σs⊆Σ，我们首先检索Σs的诱导子图G[Σs]。基于G[Σs]，我们用MDE计算树的分解T_G[Σs]。在此之后，对于每个X (v)∈T_G[Σs]，我们给每个u∈X (v) \ {v}的dist_G[Σs](v,u)，并使用哈希表将dist_G[Σs](v,u)存储在节点X (v)中。请注意，在索引中，我们还维护了从顶点v到节点X(v)的映射，以便于查询处理。
  
• Query Processing 给定一个查询q =（s，t，$\mathcal{L}$），我们可以基于在G[$\mathcal{L}$]上建立的索引T G[$\mathcal{L}$]计算dist_G^L(s,t)。具体的处理过程见算法1。它首先在T G[$\mathcal{L}$]中计算X(s)和X(t)的最近的共同祖先X_lca（第1行）。然后，它计算在X_lca中从s到顶点的距离。基于引理4.5，对于一个节点X’s及其父Xp，其中X’s是X(s)的祖先节点，并假设已经计算出从s到Xs中所有顶点的最短距离，然后从s到u∈ Xp\X’s的节点的最短距离不能用dist G[$\mathcal{L}$] (s,u) = min_w∈X′s∩X_p{dist G [$\mathcal{L}$] (s,w) + dist G[$\mathcal{L}$] (w,u)}计算，其中可以在X(w)或X(u)中查找哈希表来得到dist G[$\mathcal{L}$] (w,u)。因此，我们可以沿着从X_s到X_lca的树路径计算s到X_lca顶点们的距离（第3-11行）。t到X_lca顶点们的距离可以用同样的方法计算。最后，根据引理4.6和引理4.7，通过X_lca中的顶点得到dist G[$\mathcal{L}$] (s,t)（第13行）。
  
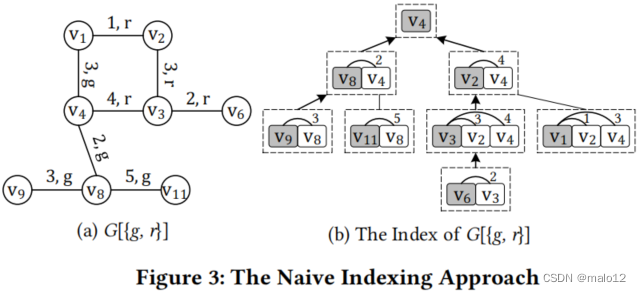
    例 4.9 重新考虑如图1 (a).所示的路网。图3 (a)显示了{g,r}的诱导子图G[{g,r}]。图3 (b)显示了由G[{g,r}]构建的相应的indexT_G[{*g,r*}]。对于T_G[{*g,r*}] 中的节点，如X(v₁)={v₁,v₂,v₄}，我们把dist_G[{g,r}](v₁,v₂) = 1和dist_G[{g,r}](v₁,v₄) = 3存储进去。对于查询q =（v₉,v₆,{g,r}），图3 (b)中的箭头演示了查询处理过程。X(v₉)和X(v₆)的LCA为X(v₄)。它沿着箭头迭代地计算从v₉和v₆到X(v₄)中顶点的最短距离。例如，当计算从v₉到v₄∈X(v₈)的最短路径时，因为X(v₉)∩X(v₈)=v₈，dist_G[{g,r}](v₉,v₄) = dist_G[{g,r}](v₉,v₈) + dist_G[{g,r}](v₈,v₄) = 5。类似的，dist_G[{g,r}](v₉,v₆) = dist_G[{g,r}](v₉,v₄) + dist_G[{g,r}](v₆,v₄) = 11。
    定理 4.10 给定一个查询q =（s，t，$\mathcal{L}$），算法1可以正确地计算出dist G[$\mathcal{L}$] (s,t)。
    定理 4.11 给定MDE生成的G的树分解T_G，对于T_G的节点X, |X∪~Xa ∈A(X)~ Xa| ≤ h，其中，A(X)代表T_G中X的祖先。
    定理 4.12 给定G的树分解T_G，对于一个节点X(v)和一个X(v)的非根祖先节点X(u)，让X_p(v)也有可能是(X_p(u))成为是X(v)也有可能是X(u)的父节点，然后{X_p(v)\X (v)}∩{X_p(u)\ X(u)} = ∅。
    定理 4.13 给定一个查询q =（s，t，$\mathcal{L}$）算法1计算dist G[$\mathcal{L}$] (s,t)的时间复杂度为O(h · ω)。

Remark

  TEDI [30]是一种最先进的基于树分解的索引方法，用于无标记道路网络上的最短路径查询，提出了一种和算法1相似的算法，时间复杂度为O（h·ω²）。如定理4.13所示，该算法的时间复杂度为O（h·ω），它将TEDI的时间复杂度降低了一个因子_ω。

5 OUR NEW INDEXING APPROACH

  如我们的实验（表2）所示，MDE通常为道路网络生成一个树高h小和树宽ω小的树分解。例如，整个美国公路网的h和ω分别为2,886和579。因此，算法1允许对一个受标签约束的查询进行有效的查询处理。然而，朴素算法需要构建2^|Σ|个单独的索引。显然，构建和维护这样2^|Σ|个单独的索引是不应该的。在本节中，我们利用边缘标记路径之间的优势关系，提出了一个基于树分解的新索引。新的索引可以通过不增加查询处理的额外成本来克服朴素索引的问题。

5.1 A New Index Structure

  重新考虑图1中的道路网络G，由于路径{v₁,v₂,v₃,v₆}的存在，在{b,g,r}的诱导子图中v₁与v₆之间的最短距离为5。同时，在{b,r}、{g,r}和{r}诱导子图中，v₁到v₆之间的最短距离也为5。在这种情况下，如果我们已经在G[{r}]构建的索引中存储了v₁和v₆之间的最短距离5，那么在G[{b,r}]、G[{g,r}]和G[{b,g,r}]构建的索引中存储相同的信息是多余的。基于这一观察，我们可以单独考虑所有可能的边缘标签集，而是将这些可能的边缘标签集作为一个整体来处理，设计一个整体的紧凑指数，覆盖所有最短距离信息，而不存储任何冗余信息。根据这个想法，我们有以下引理：
  引理 5.1 给定两个顶点u，v，设p是G中u和v的路径，如果ℓ( p ) ⊆ $\mathcal{L}$, ϕ( p ) ≤ d，则关于标签集合$\mathcal{L}$，u能在距离d到达v。
  根据引理5.1，我们将两个顶点之间的标签约束最短距离集如下：
  定义 5.2 (Label-constrained Shortest Distance Set) 给定一个道路网络G和两个G中的顶点u,v，则u,v的标签约束最短距离集（LSDS），用S(u,v)表示，是一组标签-距离对{(L₁,d₁)、(L₂,d₂),…} 且：
(1)对于每一对(L_i,d_i)∈S(u,v)，都存在一条从u到v的路径p,L_i = ℓ( p ),d_i = ϕ( p )。
(2)对于任何从u到v的路径p，都存在一个(L_i,d_i)∈S(u,v),L_i⊆ℓ( p )且d_i≤ϕ( p )；
(3)对于任何从u到v的路径p和(L_i,d_i)∈S(u,v)，如果ℓ( p )⊂L_i，则d_i <ϕ( p )；如果ℓ( p )=L_i，则d_i≤ϕ( p )。
  条件(1)确保每个标签-距离对对应G中的一个路径。条件(2)保证S(u,v)覆盖了u和v之间所有可能的受标签约束的最短距离。条件(3)保证集合最小的，根据引理5.1，对于标签约束的最短距离不存在冗余的标签-距离对。在定义5.2的基础上，对给定的G及其树分解T_G，构造标签约束的最短距离索引如下：
  定义 5.3 ((Label-constrained Shortest Distance Index) 给定一个道路网络G，T_G为其树分解，在T_G上建立G的标签约束最短距离索引，用LSD-Index表示。对于每个节点X (v)∈V(T_G)，从v到其他顶点u∈X (v)的标签约束的最短距离集被预先计算和存储。

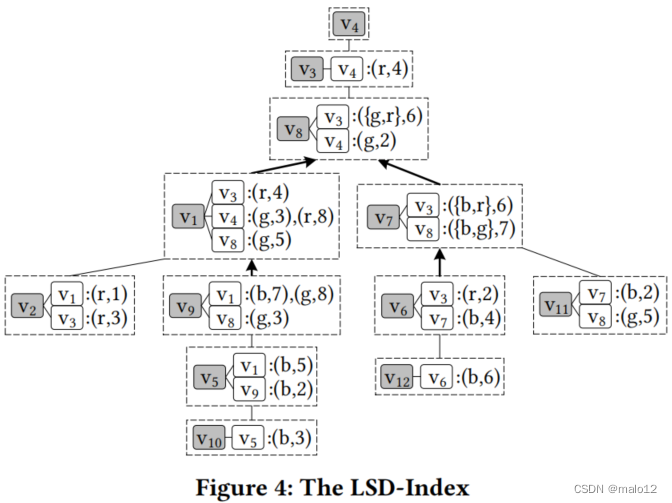
  例 5.4 图4显示了图1 (a).中G的LSD-Index。每个节点都存储相应的LSDS。以S(v₁,v₄)为例。S(v₁,v₄)={(g,3),(r,8)}，因为(1)(g,3)和(r,8)分别对应路径(v1,v4)和路径(v1,v2,v3,v4)，(2)v1和v4之间的其他路径，如(v1,v5,v9,v8,v4)，可以被这两条路径包括，(3){(g,3),(r,8)}没有冗余。

5.2 Query Processing by LSD-Index

  使用LSD-Index，我们可以很容易地获得一个类似于算法1的查询处理算法。细节见算法2。给定一个查询q =（s，t，$\mathcal{L}$），算法2首先计算X (s)和X (t)的最低共同祖先X_lca。然后，它计算到s/t沿着树路径到X_lca中顶点的标签约束距离（第3-11行）。最后，通过迭代X_lca中的顶点来计算标签约束的最短距离。过程dist计算关于边标签集L的u和v之间的标签约束最短距离，它迭代S(u,v)（第15行）中的标签-距离对（L’,d’），并返回最短的距离d’，即L’⊆L（第16-17行）。

  例 5.5 重新考虑查询q =(v₉,v₆,{g,r})，图4中的箭头演示了查询过程。X(v₉)和X(v₆)的LCA是X(v₈)。对v₉, distG{g,r}(v₉,v₁) = 8, S(v₉,v₁) 包含(g,8)。类似的，distG{g,r}(v₉,v₈) = 3. 由箭头可知,X(v₉) ∩ X(v₁) = {v₁,v₈} and X(v₁) \ X(v₉) = {v₃,v₄}. 因此distG{g,r}(v₉,v₃) = min{distG{g,r}(v₉,v₁)+distG{g,r}(v₁,v₃), distG{g,r}(v₉,v₈)+distG{g,r}(v₈,v₃)} = 9. 类似的, distG{g,r}(v₉,v₄) = 5。对于v6, distG{g,r}(v₆,v₃) = 2, distG{g,r}(v₆,v₄) = 6, distG{g,r}(v₆,v₈) =8同理。然后，distG{g,r}(v₉,v₆) = min _{w∈{v3,v4,v8}}distG{g,r}(v₉,w) + distG{g,r}(w,v₆)} = 11.
  定理 5.6 给定一个道路网络G，LSD-Index的大小为O（n·ω·ρ），其中ρ表示LSD-Index中存储的LSDS的最大大小。
  定理 5.7 给定一个查询q =（s，t，$\mathcal{L}$），算法2计算distGL(s，t)的时间复杂度为O（h·ω·ρ）。

Remark

  与朴素方法相比，在算法2的时间复杂度中引入了一个因子ρ。然而，如我们的实验（表2）所示，ρ在实践中非常小。另一方面，由于LSD-Index，我们的方法避免了在朴素方法中构建和维护2^|Σ|个单独的索引。

5.3 LSD-Index Construction

  为了构建LSD-Index，一个基于定义5.3的直接解决方案如下：我们首先对G进行树分解，然后根据定义5.2计算每个节点上的顶点的LSDS。在这种方法中，对LSDS计算的时间复杂度是 O(n · ω · (2^|Σ|)² + 2^|Σ|· (m + n logn)))。显然，这部分的成本是令人望而却步的，因此使这种方法不切实际。
  为了解决这个问题，我们提出了一种新的索引构造算法。新算法没有将构造划分为两个独立的过程，而是逐步保持部分结构LSDS通过协调树分解和LSDS计算的过程。新算法在部分LSDS的基础上，以自上而下的方式计算完整的LSDS，可以重复利用计算得到的完整LSDS，加速尚未计算的LSDS得到最终结果。在介绍该算法之前，我们在LSDS上介绍了在索引构造算法中使用的两个算子：

  定义 5.8 (Operator LSDSJoin) 给定两个LSDS S’p和S’‘p，LSDSJoin算子通过连接S’p和S’‘p中的实体生成一个新的LSDS，例如， LSDSJoin(S’p,S’‘p) = {(L′ ∪ L′′, d′ + d′′) |∀(L′, d′) ∈S’p∧ (L′′,d′′)∈S’'p}。
  定义 5.9 (Operator LSDSPrune) 给定一个LSDS S_p，LSDSPrune算子从S_p中删除（L_i,d_i），如果∃(L_j,d_j)∈S_p即 L_j ⊆ L_i ∧ d_j ≤ d_i, 当i≠j。

Algorithm 利用上述算子，我们新的索引构造算法如算法4所示。它包含以下两个阶段：在阶段1中，它进行树分解，其中计算涉及所涉及边缘的顶点对的部分LSDS（第1-18行）；在阶段2中，它基于阶段1的部分LSDS（第19-24行）以自上而下的方式计算完整的LSDS。

• Phase 1:Partial LSDS maintained tree decomposition. 在阶段1中，它按照MDE进行树的分解，并维护与分解中涉及的边相关的顶点对的部分LSDS。具体地说，它首先将G₀初始化为G，将T初始化为空树（第1行）。对于每条边(u,v)，S_p(u,v)被初始化为{(ℓ(u,v)),ϕ(u,v))}，其中S_p(u,v)用于存储部分LSDS（第2-3行）。然后，它按照MDE的过程（第4-14行）迭代地执行顶点消除。在第一次迭代中，它从G_i−1中消除了度数最小的顶点v，并将其π(·)赋值为i，其中π(·)记录了消除顺序（第5-6行）。然后，对于nbr(v,G_i−1)中的每个顶点对u,w，它首先通过LSDSJoin将S_p(v,u)和S_p(u,w)连接起来，得到S’（第8行）。如果G_i−1不包含一条边(u,w)，它向G_i中添加一条边(u,w)，并将S_p(v,w)作为S’上的LSDSPrune的结果（第9-11行）；否则，S_p(u,w)将作为S_p(u,w)∪S’上的LSDSPrune的结果进行更新（第13行）。在算法4中，为了展示的清晰，我们假设π(u) < π(w)。在消除v之后，我们把一个包含v的节点X(v)和_v的邻居nbr(v,G_i−1)添加到T中。消除所有顶点后，将生成节点之间的父子关系（第15-18行）。对于一个非根顶点_v，它选择具有最小的π（·）值的顶点u∈X (v) \ {v}（第17行），并将X (u)设置为X(v)的父节点（第18行）。
    在呈现阶段2之前，我们首先引入了标签约束最短距离（LSD）保留图G_i，其性质构成了阶段2的理论基础，也被用于算法4的证明。
    定义 5.10 (LSD Preserved Graph)给定在第1阶段生成的图G_i，G_i的LSD保留图，用GJ_i表示，是一个标记的多重图，使(1) V(GJ_i)= V(G_i)；(2)如果在Gi中有一个边e =(u,v)，那么，对于每个实体（L,d）∈Sp(u,v)，在GJ_i中有一个边e’=(u,v)，包含ℓ（e’）=L和ϕ（e’）=d。
    引理 5.11 给定两个GJ_i中的节点u,v，对于任何标签集L，dist_GJ^L(u,v)=dist_G^L(u,v)。
    根据引理5.11，GJ_i中保留了G_i中任意两个顶点之间的标签约束最短距离。此外，我们也有以下引理：
    引理 5.12 给定一个顶点v∈V（GJ_π(v)−1），对于任何边标签集L，关于G_π(v)−1中关于L的从v到u∈X (v)的标签约束最短路径只包含v和u，或者在X (v) \ {v,u}中传递一个顶点。
    因此，对于一个顶点v，如果我们已经知道任意两个顶点u,w∈X(v){v}的完整LSDS根据定义5.2，引理5.11和引理5.12，要计算完整的LSDS S(v,u)，我们只需要对任意w∈X(v){v,u}用LSDSJoin将部份的LSDS S_p(v,w)和完整的S(u,w)连接起来，将结果添加到S_p(v,u)中并用LSDSPrune去除冗余的标签-距离对。此外，我们可以利用上述步骤计算出完整的LSDS S(u,w)。根据这一想法，我们可以基于树分解以自上而下的方式计算完整的LSDS，并使用计算出的完整LSDS来加速尚未计算出的完整LSDS的计算。
• Phase 2:Top-down complete LSDS computation. 构造算法的第二阶段见算法4的第19-24行。它按照π（·）值的递减序处理顶点（第19行）。对于每个顶点v，为了计算v和u的完整LSDS，其中u ∈ X(v){v}，迭代节点w∈X(v){v,u}，通过LSDSJoin连接S_p(v,w) and S_p(u,w)，计算S’，然后使用LSDSPrune删除Sp (v,u) ∪ S′的冗余（第22-24行）。当所有节点都处理好之后，构造结束。
  
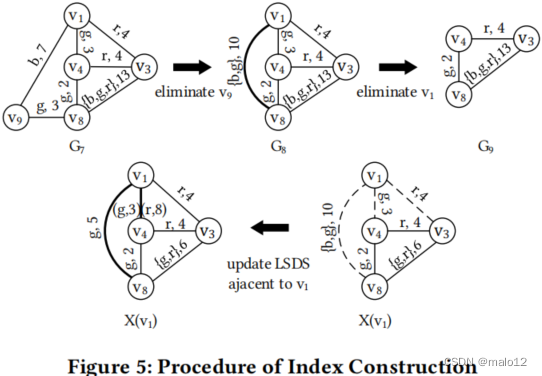
    例 5.13 在图5中，顶部(底部)说明了阶段1（阶段2）在构建图1 (a)中G的LSD-Index时的一些关键步骤，LSDS位于每条边旁。例如，在阶段1中，当从G₇中消除v₉时，添加了一条新边(v₁,v₈)，通过连接Sp(v₉,v₈)和S_p(v₉,v₁)得到S_p(v₁,v₈)={({b,g},10)}。在第2阶段，对于S(v₁,v₈)，由于LSDSJoin(S_p(v₁,v₄),S(v₈,v₄))={({g},5),({g,r},10)},({g,r},10)和({b,g},10)∈S_p(v₁,v₈)由于({g},5)而冗余，因此，S_p(v₁,v₈)被更新为{({g}、5)}。类似地，S(v₁,v₄)也被更新为{({g},3),({r},8)}。
    定理 5.14 给定一个道路网G，算法4构建该索引的时间复杂度为O（n·ω²·ρ²）。

5.4 Shortest Path Restoration

  前一节中描述的算法侧重于计算受标签约束最短距离。通过稍微修改索引结构和查询处理算法，我们可以很容易地检索到相应的标签约束最短路径。
  Augmented LSD-Index。根据定义5.2，LSD-Index中的每个实体(L,d)∈S(u,v)对应于G中的一个路径p(u,v)。为了恢复查询的最短路径，我们首先需要恢复(L,d)所表示的路径。回顾算法4中所示的LSD-Index的构建过程，有两种情况下(L,d)∈S(u,v)被生成：(1)G中的原始边(u,v)；(2)运算符LSDSJoin应用于Sp(w,u)和Sp(w,v)（第8行或第23行）。对于案例(1)，我们不在S(u,v)中存储任何额外的信息。对于情况(2)，我们在S(u,v)中除了存储(L,d)还储存(w,id_u,id_v)，导致了(L,d)的产生，id_u/(id_v)是S(w,u)/(S(w,v))对(L_u,d_u)/(L_v,d_v)的识别。利用这些附加信息，我们可以恢复S(u,v)中由(L,d)表示的路径p(u,v)：(1)p(u,v)是G中的原始边(u,v)；或(2)p(u,v)可以由p(u,w)和p(w,v)连接得到，也就是S(w,u)中的(L_u,d_u)和S(w,v)中的(L_v,d_v)，而p(u,w)和p(w,v)也可以用同样的方法递归得到。显然，由于每个实体添加的信息的大小是恒定的，因此增强的LSD-Index的空间复杂度和相应的构造算法的时间复杂度与LSD-Index的时间复杂度保持相同。
  Query processing 对于查询处理，一般的框架类似于算法2，但添加了额外的路径信息。具体地说，我们保持最短路径p(p’)从s(t)通过存储顶点v和相应的(L,d)∈S(v,u)来得到最终的d_s$\mathcal{L}$(u)在算法2的第4，10行，并将p和p‘连接到w∈X_lca，得到最短距离，见算法2的第11行。对于p(p’)中的边,并不是G(使用(L, d)∈S(v,u)表示)的原始边，它们可以通过上面讨论的方法进行恢复。给定一个q =（s，t，$\mathcal{L}$），如果返回的最短路径p有$\tau$条边,则恢复路径的额外时间复杂度可以以O（$\tau$）为界。由于回答q的下界是Ω($\tau$)，而τ与h·ω·ρ相比通常非常小，因此查询处理的时间复杂度与算法2相同。

5.5 Extension for Directed Road Networks

  在前面几节中，我们假设道路网络是无向的。我们的技术可以扩展到支持定向道路网络。
  Indexing 对于索引结构，有向道路网的LSD-Index与无向道路网的索引相似，有两个偏差：(1)对于树的分解，我们将有向道路网络的MDE扩展为如下：迭代消除具有最小度的顶点v，并在消除v后将具有有向边的任意对u,w连接起来，其他部分相同。(2)对于存储在每个节点T_G中的LSDS，我们通过使用有方向的路径，简单地扩展了在定义5.2中的标签约束距离。对于每个节点X (v)，我们预先计算并存储任何u∈X (v)的S<v,u>和S<v,u>。在这里，我们使用S<v,u>来表示从v到u的LSDS，作为有向道路网络的区别。对于索引构造算法，除了需要考虑边/路径的方向外，整个框架与算法4相同。
  Query processing 有向道路网络的查询处理过程与算法2相似。给定一个查询q =（s，t，$\mathcal{L}$），我们首先计算X(s)和X(t)的最低共同祖先X_lca。然后，我们计算了在从s到X_lca中顶点以及从这些顶点到t的标签约束的最短距离。最后，我们可以得到标签约束的从s到t的最短距离，从而恢复标签约束的最短路径从s到t的路径，其方法与所讨论的无向道路网相同。

5.6 Handling Large Σ

  虽然我们的索引技术可以显著地减少索引大小，但在某些情况下，Σ可能非常大，这使得索引大小仍然非常大。在本节中，我们将介绍如何扩展我们的技术来解决这个问题。
  人们普遍观察到，现实生活图中的标签通常遵循幂律分布[24]。因此，我们以不同的方式处理高频繁标签和低频率标签。设Σ_f为G中高频繁标签的集合。我们通过将Σ\Σf中的标签均匀地划分到|Σ_v组中，来创建一组虚拟标签Σ_v，每个虚拟标签代表每个组中的标签，其中|Σ_f|+|Σ_v|≪|Σ|。在G中，我们将相应的虚拟标签替换真实的低频标签，构建关于Σ_f∪Σ_v的LSD-Index。
  给定一个查询q =（s，t，$\mathcal{L}$），如果是L⊆Σf，我们使用算法2来直接回答这个查询。否则，设$\mathcal{L}$_f为标签集$\mathcal{L}$∩Σ_f，$\mathcal{L}$_v为表示$\mathcal{L}$∩{Σ\Σ_f }中的标签的虚拟标签集。我们根据索引和算法2计算dist_G$\mathcal{L}$_f(s,t)和dist_G$\mathcal{L}$_f∪$\mathcal{L}$_v(s,t)。显然，dist_G$\mathcal{L}$_f(s,t)>dist_G$\mathcal{L}$(s,t)，dist_G$\mathcal{L}$(s,t)>dist_G$\mathcal{L}$_f∪$\mathcal{L}$_v(s,t)>。因此，如果dist_G$\mathcal{L}$_f(s,t)=dist_G$\mathcal{L}$_f∪$\mathcal{L}$_v(s,t)，我们得到dist_G$\mathcal{L}$(s,t)。否则，最短路径可能涉及$\mathcal{L}$_v中具有虚拟标签的边，而$\mathcal{L}$中没有真实标签。在这种情况下，对于索引条目(Lv, dv)∈S(u,v)用于获得dist_G$\mathcal{L}$_f∪$\mathcal{L}$_v(s,t)和包含虚拟标签，我们需要进一步检查是否dv = dist_G$\mathcal{L}$(u,v)，这可以通过探索u的邻居w与标签$\mathcal{L}$和递归计算distG$\mathcal{L}$(w,v)。如果dv ≠ dist_G$\mathcal{L}$(u,v)，我们使用参考的distG$\mathcal{L}$(u,v)代替，可以得到最终的正确结果。

6 PARALLEL INDEX CONSTRUCTION

  虽然算法4与基于定义建立索引相比，直接显著降低了构建LSD-Index的时间成本，但由于在LSDS计算过程中不可避免的LSDSJoin和LSDSPrune操作，它的开销对于大型道路网络仍然是昂贵的。在本节中，我们通过并行化LSDS计算，进一步提高了构造效率。
  回想一下，LSDS的计算包含了阶段1中的部分LSDS维护和阶段2中的自上而下完成的完整LSDS计算。对于第1阶段的部分LSDS维护，X(v)中的Sp(v,u)的计算仅依赖于X(w)中的Sp(w,v)和Sp(w,u)，其中X(w)是树分解中X(v)的后代。对于第2阶段自上而下的完整LSDS计算，X(v)中的Sp(v,u)的计算仅依赖于X(w)中的Sp(v,w)和Sp(w,u)，其中X(w)在树分解中是X(v)的祖先。因此，我们认为：
  定义 6.1 (Tree Decomposition Level) 给定一个G的树分解T，对于节点X(v)，X(v)的树分解级别，表示为l(X(v))，l(X(v))=
其中，X(v).children表示T中的X(v)的子项。
  如上所述，如果我们根据定义6.1逐个计算LSDS层（阶段1从底层到顶层，阶段2从顶层到底层），那么，与相同级别的节点相关的LSDS计算彼此不相关，这意味着我们可以处理相关的计算所有额外的开销。

  Algorithm 根据上述思想，算法5显示了并行构造算法LSD-Index-ParCons。LSD-Index-ParCons遵循与算法4类似的框架。它首先按照MDE（第1-8行）进行树的分解。在分解过程中，它不记录部分LSDS，而是只记录导致D(u,w)中Sp(u,w)的节点v（第5行）。在完成树分解之后，它计算定义6.1之后每个节点的树分解层（第9-13行）。然后，它以自底向上的方式进行部分LSDS计算（第14-22行）和以自顶向下的方式进行完整的LSDS计算（第23-28行）。对于特定层的节点，它们被同时处理（第15-16行，第24-25行）。当算法结束时，LSD-Index被正确构造，可以证明与算法4相似。

7 EXPERIMENTS

  在本节中，我们将将我们的算法与最先进的标签约束最短路径查询方法进行比较。所有的实验都是在一台使用Intel Xeon 2.5 GHz CPU（40核）和256 GB主存运行Linux的机器上进行的。

Datasets 我们使用了DIMACS¹公开的8个可用的真实道路网络。在每个道路网络中，顶点表示道路之间的交叉点，边对应道路或路段，边的权重是两个顶点之间的物理距离，边的标签表示其道路类型。这些路网的道路类型主要可分为四类：
(1) A1、限制通行的主要公路；
(2) A2、无限制通行的主要道路；
(3) A3、次要道路、连接线；
(4) A4、地方、社区和农村道路。
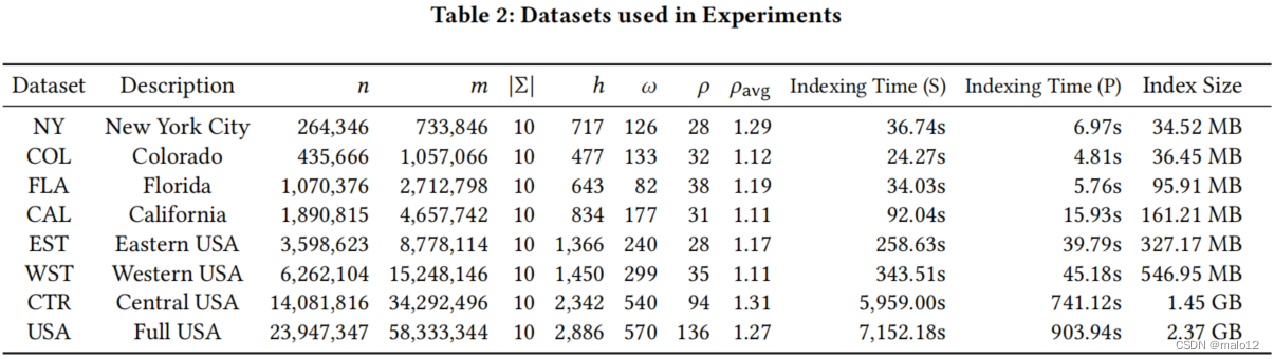
道路类型遵循幂律分布。由于不同的数据集包含不同数量的标签（从18∼32），在我们的实验（除了Exp-6），为了控制变量和保持标签的分布尽可能相同，我们引用每个数据集的标签，使每个数据集包含10标签使用以下方法：每个主要类别的标签，我们按标签频率的递增顺序排序，合并两个频率相似的标签，我们继续这个过程，直到只剩下10个标签。表2提供了关于这些数据集的详细信息。表2显示了每个道路网络的树分解的h和ω的值，很明显，h和ω在实际应用中很小。表2还显示了每个道路网的LSD-Index的ρ和ρ_avg值，其中ρ_avg表示LSD-Index中LCDS的平均大小。显然，ρ和ρ_avg在实际应用中比h和ω要小得多。
Algorithms 我们比较了以下几种算法。所有的算法都是用C++实现的，并在GCC 8.3.1中使用-O3 flag进行编译。我们采用OpenMP来实现我们的并行算法。

• Dijkstra:对给定$\mathcal{L}$的边使用Dijkstra算法直接在线搜索。
• EDP:标签约束最短路径查询的最新算法，已在第3节中介绍。
• LSD-Index:我们提出的算法包括查询处理算法（算法2）、索引构建算法（算法4）和并行索引构建算法（算法5）。
    对于EDP，我们实现了[10]中提到的所有优化技术。由于EDP在查询处理过程中逐步构建索引，为了公平起见，我们生成随机查询将EDP预热[10]，直到它的缓存大小变得稳定或达到内存限制（20GB）。
  Exp-1: Effciency when varying query distance. 在本实验中，我们通过改变查询中源顶点和目标顶点之间的标签约束最短距离来评估算法的查询效率。我们随机生成10组查询Q1，……，Q10，每组包含1000个查询。对于第i组中的每个查询q =（s，t，$\mathcal{L}$），关于L的s和t之间的标签约束距离范围为(δ/1km)^i−1/10 to (δ/1km)^i/10公里，其中，δ为道路网中任意两个顶点之间的最长距离。并将$\mathcal{L}$设置为最小边标签集，可以使s与t之间的标签约束距离满足上述条件。图6显示了四个数据集上每个组中查询的平均查询处理时间。
    如图6所示，随着距离的增加，所有算法的查询处理时间都会增加。这是因为随着s和t之间的距离的增加，需要探索更多的顶点或节点。此外，EDP总是比Dijkstra快，而LSD-Index比EDP快得多，且性能差距随着距离的增大而增大。原因是Dijkstra和EDP必须探索道路网络中的许多顶点，而LSD-Index只需要访问树分解过程中节点中的顶点，这比Dijkstra和EDP要小得多。
  Exp-2: Effciency when varying |$\mathcal{L}$|. 在本实验中，我们通过改变查询的|$\mathcal{L}$|来评估算法的查询效率。为此，我们随机生成10组查询，每组包含1,000个查询。对于每个查询q =（s，t，$\mathcal{L}$）组，$\mathcal{L}$设置为边缘标签集|$\mathcal{L}$| =i s可以达到t的边与边标签$\mathcal{L}$我们记录平均查询处理时间查询在每组和四个大型数据集的结果如图7所示，其余数据集的结果显示类似的趋势。
    根据这些结果，我们可以观察到： (1) LSD-Index总是比Dijkstra和EDP表现得至少好一个数量级。其原因与附件1中讨论的相同。(2)当我们改变|$\mathcal{L}$|时，所有算法的平均处理时间都保持稳定。对于Dijkstra和EDP，当|$\mathcal{L}$|较小时，关于$\mathcal{L}$的s和t之间的标签约束最短距离一般较大，这意味着道路网络的穿越时间较长。随着|$\mathcal{L}$|的增加，标签约束的s和t在$\mathcal{L}$之间的最短距离变小，但$\mathcal{L}$中带边标签的边数也增加。因此，在查询处理过程中，所探索的顶点和边的数量保持相似.对于LSD-Index而言，LSD-Index基于树的分解来处理查询，因此该处理几乎与$\mathcal{L}$无关。
  Exp-3: Indexing time. 表2给出了为每个数据集构造LSD-Index的时间，包括顺序构造算法和并行构造算法（使用32个线程运行）。对于前6个道路网络，即使是顺序构造算法，也可以在6分钟内构建该指标。然而，顺序构建算法需要1.5-2小时才能完成CTR和USA的索引构建。考虑到这两个数据集的大小，索引时间是可以接受的，但不是很令人满意。另一方面，对于并行构造算法，构建前6个数据集的索引需要少于60秒，构建美国数据集的索引需要少于1000秒。结果表明，我们提出的算法可以在实践中有效地构建LSD-Index，特别是并行构造算法。
  Exp-4: Index size. 各路网的LSD-Index大小如表2所示。如表2所示，前6个路网的索引大小都在1 GB以内，甚至对整个美国路网的索引大小也仅为2.37 GB。考虑到美国数据集的大小大约为0.8 GB，2.37 GB仍然很小。我们省略了EDP的索引大小，因为它的索引大小因不同的缓存策略而不同。在我们的实验设置中，我们将EDP的索引大小限制设置为20 GB，并且在我们的设置中，大多数大型道路网络（WST，CTR，USA）的索引大小都超过了10 GB。从结果中可以明显看出，LSD-Index是一个紧凑的索引结构。
  Exp-5: Case Study. 图8展示了一个受标签约束的最短路径查询的实际示例。在悉尼，我们可以简单地将道路分为三类：收费公路(T)、主要道路(M)和当地道路(L)。假设来自UNSW的学生们计划在周末开车去塔兰戈动物园。如果它们只是想尽快到达动物园，那么，它们可以通过查询q=（“UNSW”，“TarangoZoo”，“TML”）获得它们的路线，它返回15.52公里的p1。另一方面，如果他们想尽快到达动物园，但不愿意通过收费公路或当地公路，他们可以通过查询q=（“UNSW”，“TarangoZoo”，“M”）获得路线，返回p216.43公里。从这个例子中，我们可以看到，标签约束的最短路径查询可以满足不同用户在路径规划中的需求。
  Exp-6: Index size when varying |Σ|. 在这个实验中，我们评估了变化|Σ|时的指数大小。对于每个数据集，我们将标签的数量从|Σ|/5设置为|Σ|。对于较小的标签集，我们使用前面提到的类似方法生成它们：我们根据其频率对每个主要类别中的原始标签进行排序，并以相似的频率合并标签标签，直到标签数量达到所需的大小。图9显示了结果。
    图9显示，索引大小随着|Σ|的增加而增加。这是因为|Σ|越大，需要在索引中存储的信息就越多。然而，即使是美国最大的公路网，当|Σ| = 32时，最大的索引大小也是8.6GB，后者也只有数据集大小的10倍（大约0.8GB）。实验结果表明，LSD-Index是一种紧凑的指数结构。