第三章 离散数据的生成模型
3.1 介绍
在2.2.3.2中,讨论了通过生成分类器对特征进行分类,利用如下公式:,利用这个模型的关键就是对于每个类别指定一个合适的条件概率密度函数,这一章我们主要考虑的数据是具有离散的特征,同时我们也会考虑如何去推断模型的参数。
3.2 贝叶斯概念学习
概念学习,举个例子,一个小孩是如何学习狗这个概念的呢,一般在遇到狗时,家长会对小孩说,这是狗,所以都是从正例出发。一般来说不会说这不是狗,除非在小孩指着猫说这是狗,家长会给予指正。然而心理学家的研究表明,对于概念的学习,仅仅通过正的例子就可以了。
其实学习一个概念跟二项分类很像,就是学习一个函数f,如果输入是跟概念一致的,输出1,否则输出0.如果允许给出一些不确定性,也就是说用概率去描述,我们可以产生模糊集理论。
书中给出了一个叫数字游戏的例子。游戏是这样的,比如我选择一些数学上关于数的概念C,‘质数’,‘1到10之间的数’。我随即从这些概念中选一些数出来给你,然后我给一些测试样本
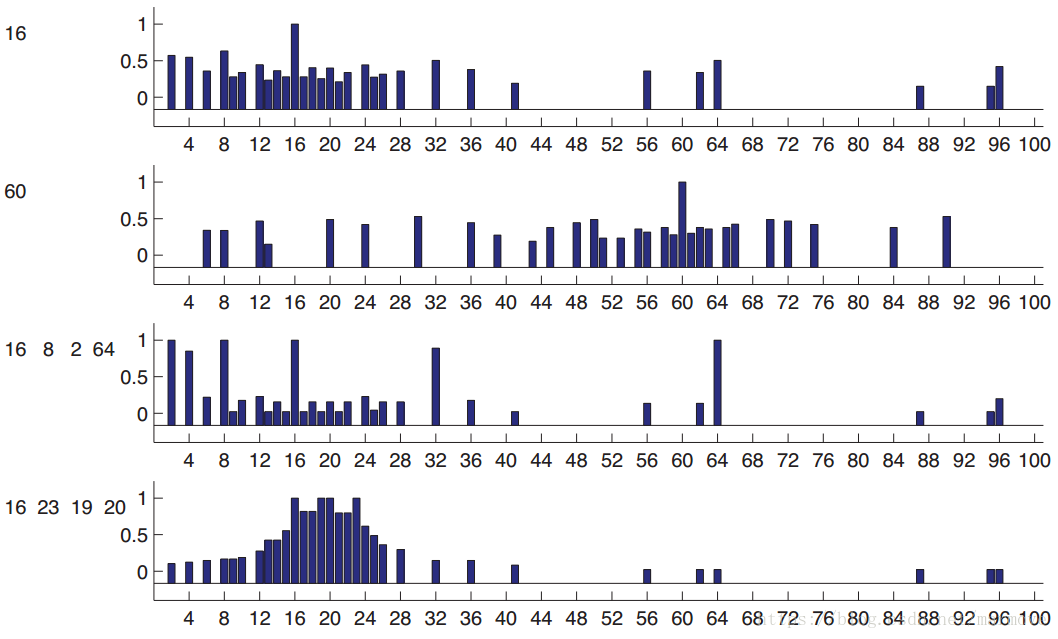
,让你找出测试样本中哪些是属于C的,哪些不属于C。为了简单起见,数都是从1-100里面取的。我们先看下图:
上图这个概率都是人工经验预测出来的。如果我只说16是正例,就是图的第一行,或者第二行图的60,当我只告诉你一个数的时候,预测会变得非常的模糊,对于16,17有可能,因为接近,2有可能,因为是偶数,所以很难判断。我们可以把每个数字所含有的概率表示为,这是后验预测分布(posterior predictive distribution)。现在我们假设,16,8,2,64是正例的话,那么就对应于第三行的图。那么这个时候你可能大概率觉得这个概念就是2的指数次方。如果我说16,23,19,20是正例,那么你可能就觉得这个概念就是20左右的数字,这对应着图的第四行。那么在实际计算机仿真当中我们该怎么做。首先我们需要一个假设空间
(hypothesis),在这里可以表示为很多的概念,比如奇数,偶数等等。那么包含数据
的假设空间叫做版本空间(version space)。但是有个问题就是,版本空间可能有很多个,比如说对于16,偶数,平方数,都是版本空间,那么哪一个的可能性最大,我们后面就要讲到如何用贝叶斯的观点去看待和解决。
3.2.1 似然
我们必须要去解释,为什么当,我们要选择‘2的指数’这个概念而不是‘偶数’这个概念。关键点就是我们要避免一些可疑的巧合,如果是偶数,那么为什么我们看到的都是2的指数呢?
我们假设从某个概念中抽取样本的时候,概率是均匀分布的。那么我们从假设h中抽取N个样本,那么概率就是:。这个就称之为似然(likelihood)。明显看出对于上面的
,如果h是‘2的指数’,似然为
,而如果h是‘偶数‘的话,那么似然为
。这里我们要强调,似然不是概率分布,积分并不等于1。
3.2.2 先验
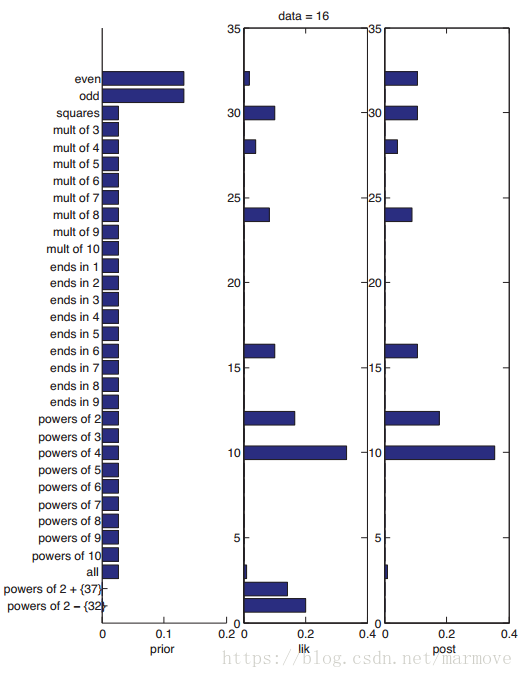
还是用上面的例子,假如有一个新的概念是‘2的指数中除了32’,就是把2的指数里面的数把32扔掉,那么明显这个概念的似然会更加的大,那么是不是这个概念更好呢?但是一个严重感觉上的问题就是这个概念太特殊了,所以说我们需要引入先验(prior)的概念。先验是很有用的,因为在很多不同的场景下,我们对一些数据的判断会不一样。针对我们之前的例子给出下图:
最左边是先验,我们看到,对于奇数和偶数因为发生的概率确实大一点,所以先验比较大,其余很多概念一样,最后类似于2的指数除去32这种概念,先验是非常小的。
3.2.3 后验
后验就是先验乘以似然然后归一化: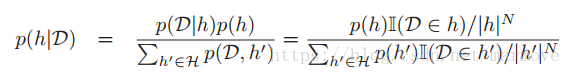
,先验似然后验的概率分布。当我们的数据量足够的多的时候,那么
就会只在一个概念的地方呈现尖峰。所以说
,这个就是delta函数。那么所以我们得到后验之后,我们通常用最大后验估计(MAP)的方法得到最终的假设。即:
。我们可以看到这个和我们之前经常用的最大似然(MLE)估计:
就是差了一个先验项。我们可以明显看到,似然是与数据量有关的,当我们的数据量越来越大的时候,先验的作用就会变得越来越微弱,MAP也就会越来越接近MLE。
3.2.4 后验预测分布
后验就是我们对于我们所要预测的东西的置信状态。而后验的可靠性往往通过你对现实的结果的观察去看你的预测是否准确。
比如在刚才的数的分类当中,,这个式子的意思我觉得写得不是很清楚:其中数据是已知的,左边就是
属于类里面的概率。右边第二项是在数据
下,不同假设的概率,右边的第一项就是在这个假设下,
是属于这个假设的概率(属于这个假设为1,否则为0)。这个也称之为贝叶斯模型平均(Bayes model averaging)。因为对于问题本身我们需要的是给你一个数据
,给你一个
,问你
是否是
里面的,并不涉及任何关于
的假设。所以上面的公式给出了对于所有的假设的加权平均,得到最终概率分布。当
的数据足够多时,其实
是一个delta函数。这个时候上面的式子就可以写作:
这个叫做plug-in approximation。后面一段主要讲MAP是很简单好用的,但是不够光滑,在数据量很少,h的分布不够尖锐的时候,可能会过拟合,数据量大一些的时候就很好用。
3.2.5 一个更加复杂的先验
一个更加复杂的先验:这是有两个先验复合而成的。第一个就是根据rule,我的理解就是这个h本身出发,后面一个是根据假设之间的相似性出发的。很细节的方面我也并没有太理解。
3.3 beta-二项式 模型
接下来就是讲一个连续的更加复杂的模型,之前讲的比较的简单。
3.3.1 似然
,这就是一个二项分布,那么其似然函数就是:
。
就是数据中值为1的样本数目,
就是数据中值为0的样本数目,总体的数据量就是
。有了
和
我们就得到了数据的全部的信息,所以称之为充分统计量(sufficient statistics)。
3.3.2 先验
我们在寻找鲜艳的时候,往往希望先验的耦合是比较容易的(在计算上),所以我们就希望先验和似然具有比较接近的形式。如果先验和后验的分布是一样的,那么我们就称该先验为共轭先验。比如说,我们的先验长这样:,那么我们的后验就可以写成:
,先验与后验具有相同的形式。所以对于伯努利分布,我们选择的先验是Beta分布:
。对于该问题,
是我们要解的参数,所以无论先验,似然,后验,都是针对
而言的。其次,a和b是
先验分布里面的参数,所以我们就称之为超参(hyper-parameters)。
3.3.3 后验
有了先验和似然,我们可以得到后验:,我们发现在这个模型下,超参其实就是伪计数,a代表了正例的计数,b则代表了反例的计数。
由于该后验与先验是一样的,所以我们可以将其应用在网络在线学习。在sequential模型中,每来一个数据,我们将之前的后验作为先验,该数据作为似然,去更新后验。所以我们可以对单个的在线的数据处理,这样就可以实现在线学习。
3.3.3.1 后验均值和重数
根据公式2.62里面的众数,我们很容易得到。如果没有任何先验的信息,那么意味着a=1,b=1,那么
。同样根据公式2.62,我们得到
的后验均值为
。后面就是通过拆解的形式,将
的后验均值拆解成只与先验有关和只与最大似然估计有关的两个部分。这告诉我们什么是后验,后验就是我们原来所相信的再加上数据告诉我们的东西,就是后验。
其中,
,
,
。很明显随着数据量的增大,
趋向于0,那么后验均值就等于最大似然估计的结果。
3.3.3.2 后验方差
根据2.62,后验方差为,如果N很大的话,那么可以近似为
,那么我们可以得到标准差
,那么是以
的速度下降。
3.3.4 后验分布估计
之前讲的都是去估计未知的参数,现在我们要考虑的是去估计新观测到的数据。那么如果我们对于参数的后验分布积分,我们可以得到:
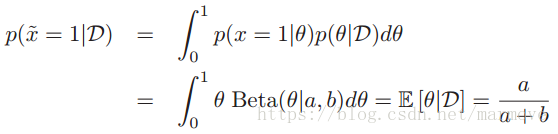
已经和前面的不一样了,书中假设这个就是后验,并不是先验。所以后面的数据就是服从以这个为参数的伯努利分布。这里要说明的是,我们在进行对于数据进行估计的时候,有两种策略,一种就是MAP,通过最大后验得到参数,也就得到了数据的概率分布,可以估计。另一种就是对于后验概率进行积分,取期望,得到数据最终的概率分布。这两种是不一样的。
3.3.4.1 过拟合和黑天鹅悖论
这一章主要就是说,如果没有先验的情况下,采样很少很可能会出现问题。比如你三次投硬币都是正面,那么按照最大似然估计,反面朝上的概率就是0,这是不合理的。即使在数据很大的情况下,由于针对个人,数据被分割,往往也会有小数据的情况,所以引入贝叶斯的方法是很有用的,无论是在数据量很小,或者即使数据量很大的某些案例下。
上面说的一种0计数的问题在哲学里面就叫做黑天鹅悖论。简单点就是你认为完全不可能存在的事情,并不代表给它0概率是合理的。事实上黑天鹅就是存在的。你扔100次硬币都是正的,不代表就没有反面的可能性。这时候我们引入一种叫做拉普拉斯平滑的方法。在这里我所理解的拉普拉斯平滑就是对于每一个count项加一个1,防止出现完全不可能的情况。
3.3.4.2 预测多次未来尝试的结果
下面我们关注的是在M次尝试中,正面朝上的次数x的概率分布,那么多次trails就是二项分布,而不是伯努利分布了,同样假设的是后验是。所以有:
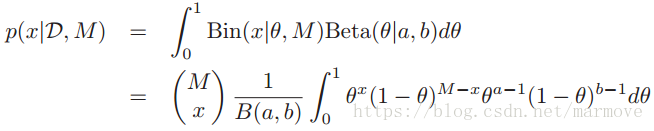
,这个分布的均值和方差具有如下的形式:
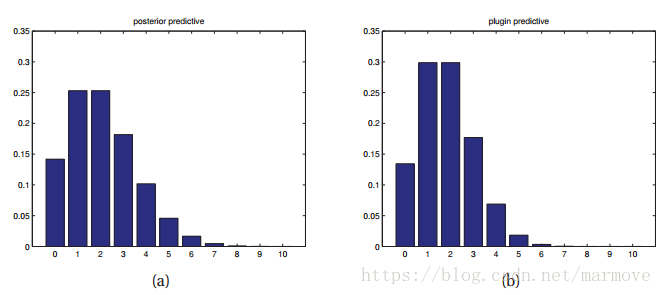
。如下图:
左边是用的后验分布去做积分得到x的后验预测分布,右边是直接用的MAP得到
,然后得到x的二项分布。比较明显,左边的尾巴更长一点,分布显得更加宽,左边更不容易出现过拟合现象。
3.4 Dirichlet-multinomial 模型
之前那一块讲的是丢硬币,接下来我们要讨论的那就是丢骰子了。
3.4.1 似然
假设我们观测到了N个数据,也就是骰子掷了N次,每个骰子有K面。,其中
。那么似然就是:
,其中
就是指出现面为k的总共有多少次,
。对比之前投掷硬币的二项分布,这个还是很好理解的。
3.4.2 先验
同样的为了就是计算的简单,我们要选择一个共轭先验,就是(狄里克雷)Dirichlet分布,具有如下的形式:
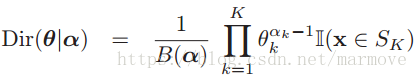
,意味着我们的
要满足每一项大于0小于1,并且求和为1。
3.4.3 后验
将先验和似然乘起来,我们得到:
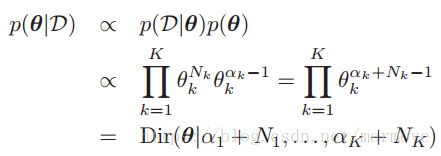
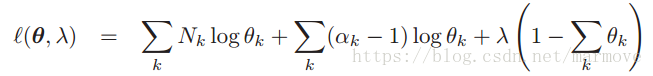
各项求和为1)消掉。接下来就是分别对
求导等于0。
,我们令
,
得到
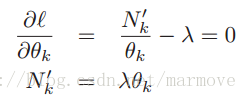
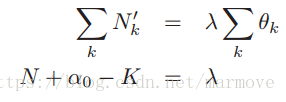
,这就是
的最大后验估计。如果是均匀分布的先验,那么
,则
。
3.4.4 后验分布估计
我们对于单个的多项的实验,后验分布估计写作:
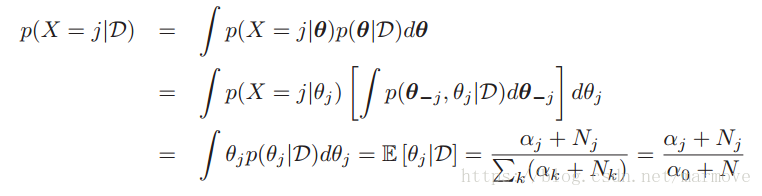
上面这个式子就避免了出现计数为0的情况,这就是贝叶斯平滑。
3.4.4.1 应用的例子:使用词袋的语言模型
上面的方法基于狄里克雷-多项分布模型,在语言模型中经常会用到。就是给你一串单词,你去预测下一个单词是什么。比如我们有如下的一系类单词:Mary had a little lamb, little lamb, little lamb. Mary had a little lamb, its fleece as white as snow. 对于词袋模型而言,我们需要知道词袋是什么:mary, lamb, little, big, fleece, white, black, snow, rain, unknown.总共这10类(标记为1,2,3,...,10)。一方面在这里没有考虑如;a, as,the这些没什么意思的单词,另一方面我们只考虑原形,比如过去式或者单复数都是一个单词。我们假设每一次单词的采样都是完全独立的,那么对于单次采样,就服从分布。对于两个句子用数字表示为:1 10 3 2 3 2 3 2 1 10 3 2 10 5 10 6 8。在这个模型中,我们不考虑顺序,直接从计数的角度出发,这就与我们之前的模型一样的。我们统计一下单次出现的数目:
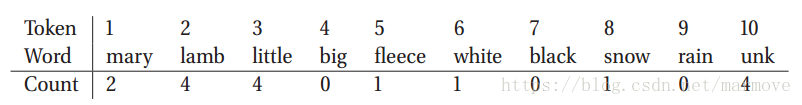
)作为先验。我们得到了后验分布估计:
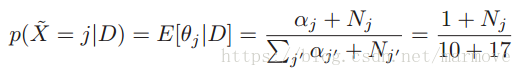
,我们发现即使之前没有出现过的单词,它的概率也并不是0,这就是贝叶斯平滑所起到的效果。所以说我们为什么要用后验分布估计,因为在无先验的情况下,MAP就和MLE一样,但是利用后验分布估计就会起到平滑的作用,即使之前没有出现的情况,也不会是概率为0。
3.5 朴素贝叶斯分类器
在这一小结中,我们考虑对于具有离散特征值的向量进行分类,。我们用生成的方法去做,那么就需要知道类条件概率分布
,然后利用公式2.13进行分类。在这里需要作一个假设,那就是特征的每一个分量关于类别是条件独立的。也就是
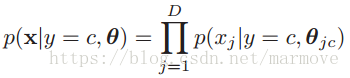
如果特征是实数的话,那我们可以使用高斯分布:。如果特征的取值只能是0或者1的话,那我们就可以选择伯努利分布:
。如果特征可以去多个种类的话,那么就使用多项分布:
。
3.5.1 模型拟合
下面就来学习一下怎么训练这个朴素贝叶斯分类器。
3.5.1.1 MLE for NBC
对于一个数据的联合概率分布就是:,这里的
其实是关于
的条件概率分布。也只有这样才能分解成连乘的形式,后面的式子是更加细化的分解。对于这个联合概率分布的似然函数,我们取一个log就是:
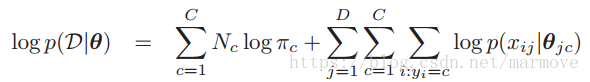
就是在类别c里面样本的总数。这里似然看似比较复杂,是因为之前的数据都是一维的,都是实验。在这里我们的数据是高维的,而且是包含输入和输出的这样一种联合概率分布,这与之前是不同的。我们进行最大似然估计就是求导。对于
来说,有一个限制,其和为1。所以利用拉个朗日乘子法,得到
。如果x的条件概率分布是伯努利分布。那么
。其中
就是属于类别c并且特征的第j维的数为1的样本的个数。其实把log似然关于
抽取出来就是
,求个导数就可以得到最大似然估计。文中给出了算法流程图,基本跟上面的解释是一样的:
3.5.1.2 贝叶斯框架下的朴素贝叶斯
最大似然估计很大的一个问题过拟合问题, 最大似然估计太过于依赖数据,当数据呈现一些极端的例子的时候,或者掺杂很多的噪声,这些信息往往有时也会被体现在我们的模型中,从而出现过拟合的情况。那么解决这个问题的一个比较简单的方法就是给定一个先验,在贝叶斯的框架下去做。使用先验如下: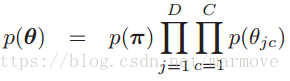
是包含整个的先验参数的。对于
来说,我们就采用狄里克雷分布
,对于每一个
来说,我们采用
作为先验,这都是之前提到的共轭先验。经常来说,我们就可以令
,这个就是对应于add-one(拉普拉斯平滑)。那么通过先验乘以似然函数,就得到了后验
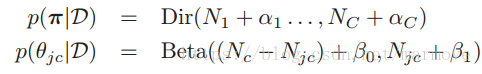
3.5.2 使用模型进行预测
最终我们就是要对模型进行预测,就是给你一个,你告诉我它是属于哪一个类别的。我们这个是生成模型,很明显就是用贝叶斯公式。所以:
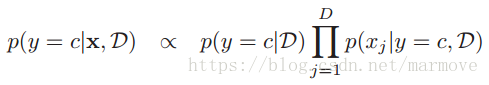
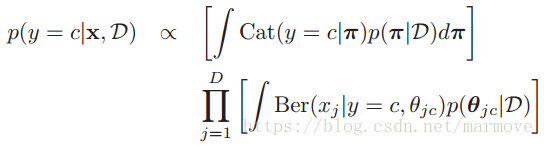
,所以就是关于
的期望,第二个积分项分成两块,一个是
,那就是
的期望,另一个就是用1去减:
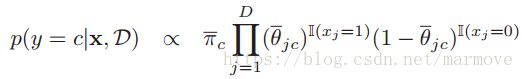
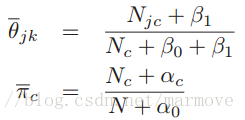
。当然我们也可以不使用后验分布估计,可以用MAP或者MLE直接进行参数的估计。这样:
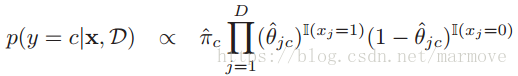
3.5.3 log-sum-exp 技巧
在实际计算的时候,尤其是在利用贝叶斯公式2.13的时候,有些项的值可能会非常的小,这样有可能造成数值下溢。所以我们对于贝叶斯法则取log: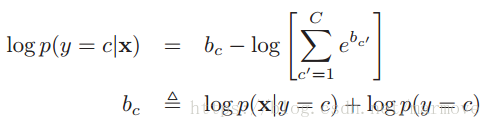
,直接求不好求,因为里面是求和。那么采用的方法就是找出指数项里面最大的,
,那么我们可以得到
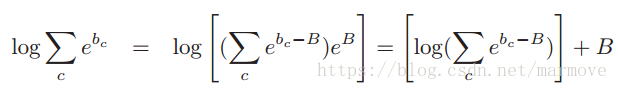
其实是比较容易的。当然如果你只需要估计类别,那么其实忽略常数项,直接最大化没有归一化的(也就是分子)就ok了。
3.5.4 使用互信息进行特征的选择
首先如果你的特征太多了,可能很多是没什么用的,那就很有可能造成过拟合。其次,我们根据上面的算法也看到了,整个计算复杂度,关于D的话是O(D),如果D特别大的话,计算的时间也会长一点,当然实际上O(D)复杂度也还好。但是总的来说,特征不能太多,尤其是多的那些特征起不了作用。
那么就要进行特征选择,去找特征与结果的关联性,然后从中取出K个。K的选择的话,就一般来说很那说,如果你要算的快,那可能K小一点,如果要精度高一点,那K就稍微大一点。这个可能就叫做filtering,ranking or screening.
一种方法就是考虑特征和类别之间的互信息:。如果互信息很小。那么特征与结果关联性就很小。式子里面是对
所有的取值和y所有的取值进行求和。如果特征是0-1分布,那么就可以写成:
,这个也好理解,直接把
带进去就可以了。
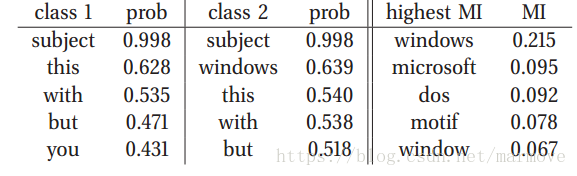
文中举了一个关于0-1分布的例子:
单词出现不出现(1,0),类别为两种。很典型的例子,subject虽然出现的多,但其实它对结果没什么影响,所以MI没有它。
3.5.5 在词袋下进行文件的分类
文件分类其实就是给你一堆文件,然后你对他进行分类,比如是否是垃圾邮件这种。那么我们如何表示一个文件呢。一个简单的方法,就是建立一个词袋,对应于一个向量,比如对于文件1,某个单词出现了,那么向量对应位置就是1,否则就是0。那么我们可以得到条件概率密度函数: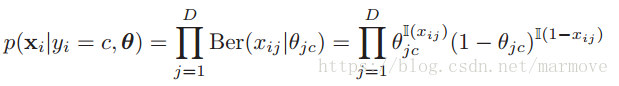
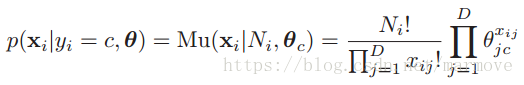
是文件的单词的总数,就对应于扔骰子的次数,
就是每一个单词出现的次数。有
。
但是上面的模型也有问题,就是有些单词可能在你训练的时候不出现,就是出现的文章很少,但是一旦出现了,就会一篇文章里面有很多这样的单词。真正影响分类的单词,有时候是不常见的,那就会导致很小,而很多其实与分类无关的单词
很大,所以这就存在很大的问题。
那么怎么做,其实就是对于加一个先验,
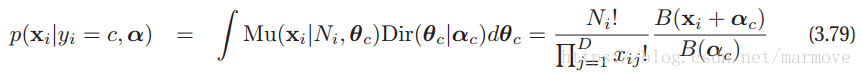























 2148
2148











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








