poj 1182 【经典并查集】 和【不一样的解法】

虽说这题很久前写过了
但是今天还是把它翻出来了

传送

动物王国中有三类动物A,B,C，这三类动物的食物链构成了有趣的环形。A吃B， B吃C，C吃A。
现有N个动物，以1－N编号。每个动物都是A,B,C中的一种，但是我们并不知道它到底是哪一种。
有人用两种说法对这N个动物所构成的食物链关系进行描述：
第一种说法是”1 X Y”，表示X和Y是同类。
第二种说法是”2 X Y”，表示X吃Y。
此人对N个动物，用上述两种说法，一句接一句地说出K句话，这K句话有的是真的，有的是假的。当一句话满足下列三条之一时，这句话就是假话，否则就是真话。
1） 当前的话与前面的某些真的话冲突，就是假话；
2） 当前的话中X或Y比N大，就是假话；
3） 当前的话表示X吃X，就是假话。
你的任务是根据给定的N（1 <= N <= 50,000）和K句话（0 <= K <= 100,000），输出假话的总数。

我翻译的是不是很好！：p）

没错，他是个中文题

分析：
知道这道题是 因为带偏移量的并查集

所以 当然先拿它来写啦！

那么 我们用
0 表示 x和y同类
1 表示 x吃y
2 表示 y吃x
那么所有的运算均在%3 的意义下进行
说几个关键也是难点的地方吧。。
第一个 路径压缩是 应该怎么更新？
很好说啦~
re[x]=(re[x]+re[f[x]])%3;
第二个
合并时候的事情，在wzc神犇的教导下，明白这玩意可以用向量解
当d=1时，a-b的偏移量是0也就是d-1
当d=2是同理

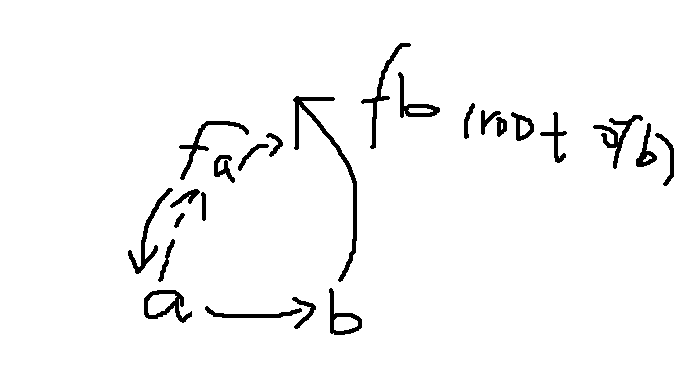
什么意思呢
我现在要报fa添进fb子节点中
那么re[fa]=(-re[a]+(d-1)+re[b]+3)%3 +3是为了判正负。

这个可ok？

剩下的那个如果祖先相同的情况大家就可以自己推一下了。。。【没错我懒了】

#include<cstdio>
#include<iostream>
#include<algorithm>

using namespace std;
 int n,k,i,num,r1,r2,d,x,y;
struct node
{

 int parent;
 int relation;
}p[50010];

int find(int x)

{
    int t;
    if(p[x].parent==x) return x;
    else
    {
        t=p[x].parent; 
        p[x].parent=find(t);
        p[x].relation=(p[t].relation+p[x].relation)%3;
}

    return p[x].parent；

}

void join()

{
    p[r1].parent=r2; 
    p[r1].relation=(3+d-1+p[y].relation-p[x].relation)%3;
}

int main()

{
    scanf("%d%d",&n,&k);
    for(i=1;i<=n;i++)//初始化 
    {
     p[i].parent=i;
     p[i].relation=0;
    }
    num=0;
    while(k--)
    {
     scanf("%d%d%d",&d,&x,&y);
     if(x>n||y>n||(d==2&&x==y))  num++;
    else
     {
         r1=find(x);
        r2=find(y);
         if(r1!=r2)
        join();
        else 
         {
             if(d==1&&p[x].relation!=p[y].relation) num++;
             else if(d==2&&(p[x].relation-p[y].relation+3)%3!=1) num++;
         }
     }
    }
    printf("%d\n",num);
    return 0;

}

关于 第二种方法 是从挑战程序设计中得到的启发。
由于N和K很大，所以必须高效地维护动物之间的关系，并快速判断是否产生了矛盾。并查集是维护 “属于同一组” 的数据结构，但是在本题中，并不只有属于同一类的信息，还有捕食关系的存在。因此需要开动脑筋维护这些关系。
对于每只动物i创建3个元素i-A, i-B, i-C, 并用这3*N个元素建立并查集。这个并查集维护如下信息：
ps 就我个人来理解 挺像关押罪犯的影集的。
① i-x 表示 “i属于种类x”。
②并查集里的每一个组表示组内所有元素代表的情况都同时发生或不发生。
例如，如果i-A和j-B在同一个组里，就表示如果i属于种类A那么j一定属于种类B，如果j属于种类B那么i一定属于种类A。因此，对于每一条信息，只需要按照下面进行操作就可以了。
1）第一种，x和y属于同一种类———合并x-A和y-A、x-B和y-B、x-C和y-C。
2）第二种，x吃y—————————合并x-A和y-B、x-B和y-C、x-C和y-A。
不过在合并之前需要先判断合并是否会产生矛盾。例如在第一种信息的情况下，需要检查比如x-A和y-B或者y-C是否在同一组等信息。（一开始我一直不明白，对于两种信息都是合并，那么以后怎么分清到底是同类还是捕食关系呢，或者说如何判断是否会产生矛盾呢？后来发现，它利用3*N的数组分3段1~N,N~2N,2N~3N分别当做是A、B、C三个种类的集合，把所有可能符合的情况都会导入进去，虽然对于两种信息的操作都是合并，但合并的内容是不一样的，这样就可以在合并之前判断其是否以另一种信息合并过或者符合另一种信息。可以自己举例来理解一下）

然后呢 cin会超时真的
然而 读入优化过后0.8s无压力
真是 喜欢上 读入优化了 ：D)

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
int n,k;
int t[1000001],x[1000001],y[1000001];
int par[500001],rel[500001];

/*
i->x,意思是i属于x种类；
i,i+n,i+2*n;意思是i->a,i->b,i->c;*/ 
int read()
{
    int x=0;
    char p=getchar();
    while(p<'0' || p>'9') p=getchar();
    while(p>='0' && p<='9') x=x*10+p-'0',p=getchar();
    return x; 
} 
int find(int r)
{
    if(par[r] == r)
    {
        return r;
    }
    else return par[r] = find(par[r]);
}

void join (int a,int b)
{
    int fa=find(a);
    int fb=find(b);
    if (fa == fb)
    {
        return ;
    }
    if(fa!=fb)
    {
        par[fa]=fb;
    }
}
bool judge(int a,int b)
{
    return find(a)==find(b);
}
int main()
{
    cin>>n>>k;
    for(int i=1;i<=n*3;i++)
    {
        par[i]=i;
    }
    int ans=0;
    for(int i=1;i<=k;i++)
    {
        int ope=read();
        int xx=read();
        int yy=read();
        if(xx>n||xx<=0||yy<=0||yy>n)
        {
            ans++;
            continue; 
        }
        if(ope == 1)  //如果x和y属于同一类 
        {
            if(judge(xx,yy+n) || judge(xx,yy+2*n))
            {
                ans++;
            }
            else{
                join(xx,yy);
                join(xx+n,yy+n);
                join(xx+2*n,yy+2*n);
            }
        }
        else{
            if(judge(xx,yy) || judge(xx,yy+2*n))
            {
                ans++;
            }
            else{
                join(xx,yy+n);
                join(xx+n,yy+2*n);
                join(xx+2*n,yy);
            }
        }
    }
    printf("%d",ans);
}