POJ图论

最新推荐文章于 2020-12-05 21:30:44 发布

mbxc816

最新推荐文章于 2020-12-05 21:30:44 发布

阅读量2.2k

点赞数

分类专栏： POJ/HDOJ 文章标签： network intervals 网络 graph construction 算法

POJ/HDOJ 专栏收录该内容

8 篇文章 0 订阅

订阅专栏

POJ 2449 Remmarguts' Date(中等) AC

http://acm.pku.edu.cn/JudgeOnline/problem?id=2449

题意：经典问题：K短路

解法：dijkstra+A*(rec)，方法很多

相关：http://acm.pku.edu.cn/JudgeOnline/showcontest?contest_id=1144

该题亦放在搜索推荐题中

POJ 3013 - Big Christmas Tree(基础) AC

http://acm.pku.edu.cn/JudgeOnline/problem?id=3013

题意：最简单最短路，但此题要过，需要较好的程序速度和，还要注意精度

解法：Dijkstra

POJ 3463 - Sightseeing(中等) AC

http://acm.pku.edu.cn/JudgeOnline/problem?id=3463

题意：最短路和比最短路大1的路的数量

解法：需要真正理解dijkstra

POJ 3613 - Cow Relays(较难) AC

http://acm.pku.edu.cn/JudgeOnline/problem?id=3613

题意：求经过N条边的最短路

解法：floyd + 倍增，贪心

POJ 3621 - Sightseeing Cows(中等) AC

http://acm.pku.edu.cn/JudgeOnline/problem?id=3621

题意：求一个环路，欢乐值 / 总路径最大

解法：参数搜索 + 最短路(ms 原始的bellman tle, 用spfa才过)

POJ 3635 - full tank?(中等) AC

http://acm.pku.edu.cn/JudgeOnline/problem?id=3635

题意：最短路变形

解法：广搜

相关：http://hi.baidu.com/hnu_reason/blog/item/086e3dccfc8cb21600e9286b.html

生成树问题

基本的生成树就不放上来了

POJ 1639 - Picnic Planning(较难)

http://acm.pku.edu.cn/JudgeOnline/problem?id=1639

题意：顶点度数有限制的最小生成树

解法：贪心 + prim/kruskal

POJ 1679 - The Unique MST(基础) AC

http://acm.pku.edu.cn/JudgeOnline/problem?id=1679

题意：判断MST是否唯一

解法：prim就行，不过还是易错的题

POJ 2728 - Desert King(中等) AC

http://acm.pku.edu.cn/JudgeOnline/problem?id=2728

题意：所谓最优比率生成树

解法：参数搜索 + prim

POJ 3164 - Command Network(难)

http://acm.pku.edu.cn/JudgeOnline/problem?id=3164

题意：最小树形图

解法：刘朱算法，这个考到的可能性比较小吧？

POJ 3522 - Slim Span(基础) AC

http://acm.pku.edu.cn/JudgeOnline/problem?id=3522

题意：求一颗生成树，让最大边最小边差值最小

解法：kruskal活用

连通性，度数，拓扑问题

此类问题主要牵扯到DFS，缩点等技巧

POJ 1236 - Network of Schools(基础) AC

http://acm.pku.edu.cn/JudgeOnline/problem?id=1236

题意：问添加多少边可成为完全连通图

解法：缩点，看度数

POJ 1659 - Frogs' Neighborhood(基础) AC

http://acm.pku.edu.cn/JudgeOnline/problem?id=1659

题意：根据度序列构造图

解法：贪心，详细证明参见havel定理

POJ 2553 - The Bottom of a Graph(基础) AC （好题）

http://acm.pku.edu.cn/JudgeOnline/problem?id=2553

出度为0的强连通分量的所有的点

POJ 2186 - Popular Cows(基础) AC （好题）

http://acm.pku.edu.cn/JudgeOnline/problem?id=2186

题意：强连通分量缩点图出度为0的点

POJ 2762 - Going from u to v or from v to u?(中等) AC

http://acm.pku.edu.cn/JudgeOnline/problem?id=2762

题意：单向连通图判定

解法：缩点 + dp找最长链 (我是用缩点+ 欧拉路判断，最后证明这方法是错的)

POJ 2914 - Minimum Cut(难) AC （难）

http://acm.pku.edu.cn/JudgeOnline/problem?id=2914

题意：无向图最小割

解法：Stoer-Wagner算法，用网络流加枚举判定会挂

POJ 2942 - Knights of the Round Table(难)

http://acm.pku.edu.cn/JudgeOnline/problem?id=2942

题意：求双联通分量(或称块)中是否含奇圈

解法：求出双连通分量后做黑白染色进行二分图图判定

相关：http://hi.baidu.com/zfy0701/blog/item/57ada7ed104ce9d2b31cb104.html

POJ 3177 - Redundant Paths(中等) AC

http://acm.pku.edu.cn/JudgeOnline/problem?id=3177 （和3352一样）

题意：添加多少条边可成为双向连通图（任意两点间有两条不共边的路径）

解法：把割边分开的不同分量缩点构树，看入度

公式：入度为1的leaf个数， ( leaf + 1 ) / 2

POJ 3352 - Road Construction(中等) AC

http://acm.pku.edu.cn/JudgeOnline/problem?id=3352 （和3177一样）

题意：添加多少条边可成为双向连通图（当删除任意一条边的时候，图还保持连通性）

解法：把割边分开的不同分量缩点构树，看入度 ( leaf + 1 ) / 2

建议对比下1236，有向图添加多少条边变成强连通图

POJ 3249 - Test for Job(基础)

http://acm.pku.edu.cn/JudgeOnline/problem?id=3249

解法：bfs / dfs + dp

POJ 3592 - Instantaneous Transference(基础) AC

http://acm.pku.edu.cn/JudgeOnline/problem?id=3592

解法：缩点，最长路，少人做的水题，注意细节（和 3160 类似）

POJ 3687 - Labeling Balls(中等) AC （莫名其妙，有空再重新看）

http://acm.pku.edu.cn/JudgeOnline/problem?id=3687

解法：拓扑排序

POJ 3694 - Network(中等)

http://acm.pku.edu.cn/JudgeOnline/problem?id=3694

解法：双连通分量+并查集

2-SAT问题

此类问题理解合取式的含义就不难

POJ 2723 - Get Luffy Out(中等) AC （好题）

http://acm.pku.edu.cn/JudgeOnline/problem?id=2723

解法：二分 + 2-SAT判定

POJ 2749 - Building roads(较难) AC

http://acm.pku.edu.cn/JudgeOnline/problem?id=2749

解法：二分 + 2-SAT判定

POJ 3207 - Ikki's Story IV - Panda's Trick(基础) AC

http://acm.pku.edu.cn/JudgeOnline/problem?id=3207

解法：简单的2-sat，不过其他方法更快

POJ 3648- Wedding(中等) AC

http://acm.pku.edu.cn/JudgeOnline/problem?id=3648

解法：用2-sat做会比较有意思，但是暴搜照样0ms

POJ 3678 - Katu Puzzle(基础) AC

http://acm.pku.edu.cn/JudgeOnline/problem?id=3678

解法：直接按合取式构图验证就行了（本质）

POJ 3683 - Priest John's Busiest Day(中等) AC

http://acm.pku.edu.cn/JudgeOnline/problem?id=3683

解法：n^2枚举点之间的相容性构图，求解2-SAT (要求输出方案)

POJ 2296 Map Labeler (中等) (第七道)AC

http://poj.org/problem?id=2296

解法：上下边形成2元关系。然后构完图，求2-SAT

POJ 3905 Perfect Election(中等) (第八道) AC

http://poj.org/problem?id=3905（好题！）

解法: 建好矛盾，直接就是2-SAT

最大流问题

变形很多，最小割最大流定理的理解是关键

POJ 1149 - PIGS(较难) AC （灰常好题！强烈推荐）

http://acm.pku.edu.cn/JudgeOnline/problem?id=1149

绝对经典的构图题

POJ 1273 - Drainage Ditches(基础) AC

http://acm.pku.edu.cn/JudgeOnline/problem?id=1273

最大流入门

POJ 1459 - Power Network(基础) AC

http://acm.pku.edu.cn/JudgeOnline/problem?id=1459

基本构图

POJ 1637 - Sightseeing tour(Crazy) AC

http://acm.pku.edu.cn/JudgeOnline/problem?id=1637

题意：求混合图的欧拉迹是否存在

解法：无向边任意定向，构图，详建黑书P324

POJ 1815 - Friendship(中等) AC

http://acm.pku.edu.cn/JudgeOnline/problem?i1d=815

题意：求最小点割

解法：拆点转换为边割

相关：http://hi.baidu.com/zfy0701/blog/item/a521f230b06dea9fa9018e0e.html

POJ 1966 - Cable TV Network(中等) AC

http://acm.pku.edu.cn/JudgeOnline/problem?id=1966

题意：去掉多少点让图不连通

解法：任定一源点，枚举汇点求点割集(转换到求边割)，求其中最小的点割

POJ 2112 - Optimal Milking(基础) AC （好题）

http://acm.pku.edu.cn/JudgeOnline/problem?id=2112

二分枚举，最大流

POJ 2391 - Ombrophobic Bovines(中等) AC （好题）

http://acm.pku.edu.cn/JudgeOnline/problem?id=2391

题意：floyd, 拆点，二分枚举

相关：http://hi.baidu.com/zfy0701/blog/item/3e0006c4f73f0eaf8226acff.html

POJ 2396 - Budget(中等)

http://acm.pku.edu.cn/JudgeOnline/problem?id=2396

题意：有源汇的上下界可行流

解法：用矩阵-网络流模型构图，然后拆边

相关：http://hi.baidu.com/zfy0701/blog/item/6449d82a64e15e3e5343c1ba.html

最小割模型在竞赛中的应用

POJ 2455 - Secret Milking Machine(基础) AC （好题）

http://acm.pku.edu.cn/JudgeOnline/problem?id=2455

二分枚举，一般来说需要写对边容量的更新操作而不是每次全部重新构图

POJ 2699 - The Maximum Number of Strong Kings(较难)

http://acm.pku.edu.cn/JudgeOnline/problem?id=2699

解法：枚举人数 + 最大流(感谢xpcnq_71大牛的建图的提示)

POJ 2987 - Firing(较难) AC （经典）

http://acm.pku.edu.cn/JudgeOnline/problem?id=2987

题意：最大权闭包

解法：先边权放大，第一问总量-最大流，第二问求最小割

相关：http://wywcgs.spaces.live.com/blog/cns!4D861A02A3382142!1109.entry?&_c02_owner=1

RQNOJ 最大获利Profit(中等) AC （经典）

http://www.rqnoj.cn/Problem_556.html

最大权闭包图的特殊情况

ZOJ 2071 - Technology Trader AC

http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemCode=2071

也是此类型，最大权闭包图。多加了输出买哪些组件，使效益最大。

POJ 3084 - Panic Room(中等，好题)

http://acm.pku.edu.cn/JudgeOnline/problem?id=3084

题意：略

解法：根据最小割建模

POJ 3155 - Hard Life(很挑战一题) AC （难）

http://acm.pku.edu.cn/JudgeOnline/problem?id=3155

题意：最大密度子图

解法：参数搜索 + 最大权闭合图，A.V.Goldberg的论文(nb解法)

最小割模型在信息学竞赛中的应用一文中也有讲

POJ 3189 - Steady Cow Assignment(中等)

http://acm.pku.edu.cn/JudgeOnline/problem?id=3189

题意：寻找最小的区间完成匹配

解法：这题充分说明SAP的强大，纯暴力可过。更好的方法是在枚举区间的过程中不断删边和加边继续网络流过程

POJ 3204 - Ikki's Story I - Road Reconstruction(基础)

http://acm.pku.edu.cn/JudgeOnline/problem?id=3204

ZOJ 2532 - Internship(基础)

http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemCode=2532

题意：确定边是否是某个割中的边

解法：两边dfs求割, 或暴力枚举(需要写取消某条增广路的操作(但数据弱，也许不取消也能混过))

POJ 3308 - Paratroopers(较难)

http://acm.pku.edu.cn/JudgeOnline/problem?id=3308

POJ 2125 - Destroying The Graph(难)

http://acm.pku.edu.cn/JudgeOnline/problem?id=2125

题意：最小点权覆盖

POJ 3469 - Dual Core CPU(中等)

http://acm.pku.edu.cn/JudgeOnline/problem?id=3469

题意：最小割

POJ 3498 - March of the Penguins(中等)

http://acm.pku.edu.cn/JudgeOnline/problem?id=3498

题意：满足点容量限制的网络流

解法：拆点把点容量转换为边容量，枚举汇点

ZOJ 2587 - Unique Attack(较难)

http://acm.zju.edu.cn/show_problem.php?pid=2587

题意：确定最小割是否是唯一的

解法：得理解dfs求最小割算法的本质

SPOJ 839 - Optimal Marks(难)

http://www.spoj.pl/problems/OPTM/

题意：略

解法：很经典哦，见amber的集训队论文，根据标号的每一位求最小割

SGU 326 - Perspective(中等)

http://acm.sgu.ru/problem.php?c0&problem=326

比较经典的构图法

费用流问题

可以KM解的就不放在这里，另外，感觉除非很特殊的图，一般用连续增广路的算法就够了

POJ 2175 - Evacuation Plan(中等)

http://acm.pku.edu.cn/JudgeOnline/problem?id=2175

题意：判断是否给定解是最优解，比较阴的一题

解法：根据给出的计划构造流，然后消且只消一次负圈

POJ 3422 - Kaka's Matrix Travels(中等)

http://acm.pku.edu.cn/JudgeOnline/problem?id=3422

题意：略

解法：拆点

POJ 3680 - Intervals(较难)

http://acm.pku.edu.cn/JudgeOnline/problem?id=3680

题意：略，这题还是蛮经典

解法：discuss中比较详细

SPOJ 371 - Boxes(简单)

http://www.spoj.pl/problems/BOXES/

题意：略

解法：费用流，但似乎有比网络流更好的做法

SGU 185 - Two shortest(中等)

http://acm.sgu.ru/problem.php?c0&problem=185

题意：求两条不想交的最短路径

解法：费用流，也可以最短路 + 最大流。

匹配问题

正确理解KM算法是很重要的

这里我还要说几句：最正确解最小权匹配的办法是用一个很大的数-当前边权值，而不是直接对边权取反(这样只能处理左右点相等的完全二分图，即K(n, n)

以上有可能还是说的有点问题，以后补充

POJ 1486 - Sorting Slides(中等)

http://acm.pku.edu.cn/JudgeOnline/problem?id=1486

题意：二分图的必须边

解法：需正真理解最大匹配算法，详见http://hi.baidu.com/kevin0602/blog/item/1d5be63b5bec9bec14cecb44.html

POJ 1904 - King's Quest(中等，好题)

http://acm.pku.edu.cn/JudgeOnline/problem?id=1904

题意：求二分图所有可能的匹配边

解法：虽然最终不是用匹配算法，但需要理解匹配的思想转换成强连通分量问题。

POJ 2060 -Taxi Cab Scheme(基础)

http://acm.pku.edu.cn/JudgeOnline/problem?id=2060

题意：最小路径覆盖

POJ 2594 -Treasure Exploration(中等)

http://acm.pku.edu.cn/JudgeOnline/problem?id=2594

题意：可相交最小路径覆盖

解法：先传递闭包转化下

POJ 3041 - Asteroids(基础) AC

http://acm.pku.edu.cn/JudgeOnline/problem?id=3041

解法: 简单行列匹配

POJ 2226 - Muddy Fields(基础)

http://acm.pku.edu.cn/JudgeOnline/problem?id=2226

题意：行列的覆盖

解法：最小点集覆盖 = 最大匹配

POJ 2195 - Going Home(基础) AC

http://acm.pku.edu.cn/JudgeOnline/problem?id=2195

题意：最小权值匹配

解法：KM算法

POJ 2400 - Supervisor, Supervisee(中等)

http://acm.pku.edu.cn/JudgeOnline/problem?id=2400

题意：输出所有最小权匹配

解法：KM, 然后回溯解，汗，输入的两个矩阵居然是反过来的

POJ 2516 -Minimum Cost(中等)

http://acm.pku.edu.cn/JudgeOnline/problem?id=2516

题意：最小权值匹配或最小费用流

解法：拆点 + KM算法(只有正确的才能过)，费用流(ms错的可能也能过)

POJ 3686 - The Windy's(较难)

http://acm.pku.edu.cn/JudgeOnline/problem?id=3686

题意：最小权值匹配

解法：拆点,然后尽管用KM算法去水吧，数据其实弱得不得了 O(50 * 50 * 2500) -> 16ms

相关：http://hi.baidu.com/kevin0602/blog/item/2829dc01d7143b087bec2c97.html

SPOJ 412 - K-path cover(较难)

https://www.spoj.pl/problems/COVER/

题意：略

解法：很牛叉的一道匹配

相关：http://hi.baidu.com/roba/blog/item/c842fdfac10d24dcb48f31d7.html

SGU 206. Roads(较难)

http://acm.sgu.ru/problem.php?c0&problem=206

解法：经典题目，也可以使用spoj 412那题的优化

NP问题

一般是搜索或dp解的

POJ 1419 - Graph Coloring(基础)

http://acm.pku.edu.cn/JudgeOnline/problem?id=1419

题意：图的着色

解法：搜索，可惜题目的数据真是太弱了

POJ 2989 - All Friends(难)

http://acm.pku.edu.cn/JudgeOnline/problem?id=2989

题意：极大团数量

解法：开始狂tle, 后来找了论文：Finding All Cliques of an Undirected Graph（Coen Bron & Joep Kerboscht）

ZOJ 1492 - Maximum Clique(基础)

http://acm.zju.edu.cn/show_problem.php?pid=1492

题意：图的最大团

解法：搜索，如果要求速度，可参考下相应论文

其他

不能成大类的

POJ 1470 - Closest Common Ancestors(基础)

http://acm.pku.edu.cn/JudgeOnline/problem?id=1470

题意：LCA问题

解法：tarjan或RMQ，另外输入很恶心

POJ 1985 - Cow Marathon(基础)

http://acm.pku.edu.cn/JudgeOnline/problem?id=1985

题意：树上的最长路径

解法：dp

POJ 1986 - Distance Queries(中等)

http://acm.pku.edu.cn/JudgeOnline/problem?id=1986

题意：LCA

解法：tarjan或RMQ

HOJ 11192 - Justice League(有趣的图论)

http://acm.hnu.cn:8080/online/?action=problem&type=show&id=11192&courseid=99

HOJ 11277 - New Island(有趣的图论)

http://acm.hnu.cn:8080/online/?action=problem&type=show&id=11277&courseid=109

本文转载自: http://blog.csdn.net/logic_nut/archive/2009/08/27/4491326.aspx

====================================================================================================

1062* 昂贵的聘礼

解法：枚举等级限制+最短路

交易过程中等级最高和最低的差小于m

1087* A Plug for UNIX (HDU1526)

解法：2分匹配

调制器无限，用floyd传递插口转换，然后就是2分匹配

1094 Sorting It All Out

解法：floyd + 拓扑排序

先用floyd判断自环（或用Tarjan），拓扑判断是否能确定序列

1112* Team Them Up! 2分图染色+DP (ZOJ1462)

1125 Stockbroker Grapevine

解法：floyd

FLOYD,然后求每个点到其他点的最短时间和

1135 Domino Effect (ZOJ1298)

题意：有n个关键骨牌 (1 <= n < 500)，m列骨牌。整个多米诺骨牌图是联通的。

m列骨牌描述如下：a,b,i，表示这排骨牌是在关键骨牌a到b之间的，从一头到另一头倒下需要i秒。

总是从n=1的骨牌开始推倒。输出最后倒下的骨牌的倒下时间和位置（最后倒下的是某个关键骨牌，或者某两个关键骨牌之间）

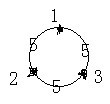数据二的图形，可看出，最后倒的在2,3中间位置。

解法：最短路

求出骨牌1到其他骨牌的最短路，最后倒下的是某个关键骨牌，或者某两个关键骨牌之间

1149* PIGS

题意：有M个猪圈(M<=1000),每个猪圈里初始时有若干头猪

   一开始所有的猪圈都是关闭的.

   一次来了N个顾客(N<=100) , 每个顾客分别会打开指定的几个猪圈,从中买若干头猪

   每个顾客分别有他能够买的数量的上限.

   每个顾客走后,他打开的猪圈中的猪可以任意给调换到其他开着的猪圈里,然后所有猪圈从新关上.

   问:总共最多能卖出多少头猪.

解法：分层网络流

     可以把猪圈分层建边，但是节点数要10W。有更优秀的建边方法

   请移步这里

1161* Walls

解法：floyd

   将区域作为顶点，如果两个区域邻接(有公共边)，就连边，权值为1

   注意:输入区域的点的顺序(顺逆时针)

   以此建图，用floyd算法算出每个顶点间的最短距离,然后就是穷举每个顶点。

   使每个俱乐部的成员到(所在村庄)达该顶点的距离之和最小

   村庄到区域的距离即：将村庄作为点的区域(顶点)到枚举顶点的距离

1201 Intervals

解法：差分约束

约束条件：s[b]-s[a-1] >= c ， 0 <= s[i+1]-s[i] <= 1

1236* Network of Schools

题意：问添加多少边可成为完全连通图

解法：基础强联通

缩点，看度数

1251 Jungle Roads

解法：基础最小生成树

1273 Drainage Ditches

解法：基础最大流

注意输入时先输边数n，再是点数m

1274 The Perfect Stall

题意：牛和挤奶器最大匹配

解法：基础二分匹配

1275* Cashier Employment (神题)

解法：差分约束

ti[i] 表示从 i 开始工作的人数，s[i] 表示 0-i 总共雇佣了多少人， r[i] 表示 i 所需的至少人数

   ti[i-7]+ti[i-6]+...ti[i] >= r[i] ( 表示前8小时开始工作的人数 )

   设：s[i]-s[i-8] = ti[i-7]+ti[i-6]+...ti[i]

   0 <= S[i]-S[i-1] <= ti[i]

   约束条件：①S[i]-S[i-1] >= 0 ②S[i-1]-S[i] >= -ti[i]

   ③S[i]-S[i-8] >= r[i] ( i>=8 ) ④S[23]+S[a]-S[a+16] >= r[i] ( i<=7 ) ==> S[a]-S[a+16] >= r[i]-S[23]

       ⑤*注意：S[24]-S[0]>=mid //这句话要记得

1325 Machine Schedule

解法： 二分匹配(最小点覆盖)

最小点覆盖：选取最少的点数，使这些点和所有的边都有关联（选择最少的点覆盖所有的边）

1364 King

解法：差分约束

     gt： s[a+b]-s[a-1]>c  ==> s[a+b]-s[a-1]>=c+1

   lt： s[a+b]-s[a-1]<c ==> s[a-1]-s[a+b]>(-c)

   超级源点： s[i]-s[n+1] >= 0

1422 Air Raid

解法：二分匹配 (最小路径覆盖)

（伞兵） 最小路径覆盖：用最少的不相交简单路径覆盖所有结点。

有向图：ans = n - match() ，无向图： ans = n - ( match() +1 ) / 2

1459 Power Network

解法：基础网络流

1466 Girls and Boys

解法：二分匹配 ( 最大独立集 )

最大独立集 = 顶点数 - 最小点覆盖

由于最小点覆盖所有边，所以去掉这些点后，剩下的点之间就没有关联边，即互相独立

1469 COURSES (HDU1083)

解法：二分匹配(完全匹配 )

1502 MPI Maelstrom

题意：计算从1发送信息到其他n-1个点最短时间 , 并且信息是同时发出去的

解法：最短路

计算1到其他n-1个点的最短时间，再取最大即可(因为信息是同时发的)

1511* Invitation Cards (HDU1535)

解法：最短路

来回最短路(单向): 正向建边 , 可以计算出S到任意点的最短路。

反向建边,那么S到任意点的最短路就相当于从任意点回来S的最短路

1637* Sightseeing tour

解法：混合欧拉回路

单向边：无用，删 in[b]++ ; out[a]++

   双向边：随意定向 in[b]++ ; out[a]++

   【建图】x = in[i]-out[i]

   ①如果x是奇数，肯定不存在欧拉回路

   ②如果x>0 (入>出) 连 i -> T 容量： x/2

   ③如果x<0 (入<出) 连 S -> i 容量：-x/2

   【判断】是否满流

1716 Integer Intervals

题意：和1201一样

解法：差分约束

① s[b+1]-s[a]>=2 ② 0 <= s[i+1]-s[i] <= 1

③ s[i]>=0 (第③个是建超级源点的条件，这里可以不要)

1724* ROADS

解法：带限制的最短路

方法① 将每个点拆分，开二维 dis[ i ][ j ] 记录。表示到达节点 i 总共花费 j 的金钱所需的最短路 ( j<=K )

方法②广搜bfs() + 优先队列

1734 Sightseeing trip

解法：Floyd 求最小环 + 输出路径

[cpp] view plain copy

void floyd() { // 最小环模板
int i,j,k,w,v;
d=inf;
for(i=1;i<=n;i++)
for(j=1;j<=n;j++) path[i][j]=j,dis[i][j]=e[i][j];
for(k=1;k<=n;k++) {
//新增部分,求最小环
for(i=1;i<k;i++) if(e[i][k]!=inf)
for(j=1;j<i;j++) if(e[k][j]!=inf) {
if(dis[i][j]==inf) continue;
if(d>dis[i][j]+e[i][k]+e[k][j]) {
d=dis[i][j]+e[i][k]+e[k][j];
// 记录路径
len=0; s[0]=k; v=i;
while(v!=j) s[++len]=v,v=path[v][j];
s[++len]=j;
}
}
//通常的floyd部分
for(i=1;i<=n;i++) if(dis[i][k]!=inf)
for(j=1;j<=n;j++) if(dis[k][j]!=inf)
if(dis[i][j]>dis[i][k]+dis[k][j])
dis[i][j]=w , path[i][j]=path[i][k];
}
}

1780* Code （好题）

题意：要求所有的n位数编码成一个数字串，每个n位数只出现一次

解法：欧拉回路

可以把n位数看成边，那么可以把它的前n-1位看成点A，后n-1一位看成点B，

那么它就是A->B的一条边。找一次欧拉回路就行了。

此题要用栈模拟递归函数！！！

1789 Truck History

解法：最小生成树( prim 或 kruskal)

1797 Heavy Transportation

解法：最小生成树或最短路或 dfs

二分枚举下限，用最小生成树或最短路或 dfs 判断 1 和 n 是否连通

1847 Tram

解法：简单最短路

1904* King's Quest 强联通

1949 Chores

解法：最短路

反向建图 建立超级源点S=0 ，连接入度为0 的点，边权为 0

   点 i 和 prerequisites ( j ) ， i 连 j ，边权为 time[ i ]

   然后求最长路

   PS: 正向建边，不知道哪里错了，一直TLE

2060 Taxi Cab Scheme

解法：二分匹配 (最小路径覆盖)

2075 Tangled in Cables

解法：最小生成树

2112 Optimal Milking

解法：二分+网络流

二分最远距离，建可行边，判断是否符合要求

2125 Destroying The Graph

解法：最小割(最小点权覆盖)

最小点权覆盖：最小点权覆盖所有的边（等同于最大独立集）

拆点并将点权转成边权。

i 和 i+n 分别表示出入，S 连 i 删出边的权， i+n 连 T 删入边的权。求最小割。

2135 Farm Tour

题意：无向图，从起点到终点，再从终点到起点。不能走重复的边。求最短路程。

解法：费用流

相当于找两条从起点到终点不重复的路径。
S 连起点，容量2 费用0 ， 终点连 T，容量2 费用0

拆边： i 连 j ，j 连 i 容量1 ，费用边权w

2139 Six Degrees of Cowvin Bacon

题意：类似 HDU1869 六度分离

这里求的是以哪个人 i 为中心，到其他人的分离度的平均值最小，求最小值

解法： Floyd

相当于求 i 到其他人的距离总和最小，最后 avg = sum*100 / (n-1) 即可

2226 Muddy Fields

题意：用最少的木板覆盖所有的muddy，且木板不能覆盖到草地

解法：二分匹配 (行列匹配)

拆行和拆列(一行拆成多行)，把每一行连续的 * 看做一“行”，把每一列连续的 * 看做一“列”

再对每一个 * 所对应的 “行” 和 “列” 连边，求二分匹配

2230 Watchcow

题意：无向图，从1出发经过每条边2次回到1。输出路径

解法：欧拉回路

拆无向边为有向边，a->b b->a ，就变成了每条边经过一次的欧拉回路。从1做一次欧拉就可以了

2239 Selecting Courses

解法： 基础二分匹配

2267* From Dusk till Dawn or: Vladimir the Vampire 最短路

2289 Jamie's Contact Groups (HDU1669)

解法：二分+二分图多重匹配 (或二分答案+网络流)

2296 Map Labeler

解法：2-Sat (二分枚举答案)

2337 Catenyms

解法：欧拉路径

①用并查集判断连通性

②判断入度和出度是否满足

欧拉回路-> 入度=出度

欧拉路径-> 只有一个,入度-出度=1 ; 只有一个,出度-入度=1

2349 Arctic Network

题意：有卫星电台的城市之间可以任意联络。没有卫星电台的城市只能和距离小于等于D的城市联络。题目告诉你卫星电台的个数S，让你求最小的D.

做最小生成树，去掉最长的S条边后，剩下最长的边就是D.

也就是求最小生成树中第S+1长的边。

解法：最小生成树

2367 Genealogical tree

解法：基础拓扑排序

2387 Til the Cows Come Home

解法：基础最短路

2391* Ombrophobic Bovines

解法：二分+网络流

S 连 i (牛) 容量: 牛的数量

i+n (棚) 连 T 容量: 能hold牛的个数

i 连 j+n 容量:inf (表示可行流)

PS: const ll inf=9999999999999999ll; up=inf (上界) WA

up=9999999999999999ll AC

2394 Checking an Alibi

题意：给你无向图，两点间花费的时间。再给你每个牛所在的位置。

给定一个time ，问你那些牛可以在time时间内到达 1

解法：最短路

2396* Budget 上下界网络流

2421* Constructing Roads

解法：基础最小生成树

2446 Chessboard

题意：去掉k个洞，剩下的点能不能用1X2的矩形完全覆盖

解法：二分匹配

相连的2点进行匹配，判断是否是完全匹配

2455 Secret Milking Machine

解法：二分+网络流

注意重边也要！

2457 Part Acquisition

解法：最短路 (输出路径)

2472 106 miles to Chicago

解法：最短路

求边乘积最大，将其化成对数，就是加起来最大。让后就是裸的最长路了

2485 Highways

解法：基础最小生成树

2516 Minimum Cost 费用流

2536 Gopher II

解法：基础二分匹配

2553* The Bottom of a Graph

解法：强连通

出度为0的点，它们能到达的点V，V都能到达它们

2570 Fiber Network floyd

2584 T-Shirt Gumbo 网络流

2594* Treasure Exploration

解法：floyd传递性+二分匹配(最小路径覆盖)

2723 Get Luffy Out

解法：二分+2-Sat

2-Sat的本质就是：一件物品选了，对另一件物品的影响。

每个物品有2个状态：选，不选。即 x 和 ~x

如 x y 。选了x，y钥匙就会消失。那么选了x就不能选y，即选了x就选 ~y (非y)

2724 Purifying Machine 2分匹配

2728 Desert King 最优比例生成树

2749* Building roads (好题!)

解法：二分+2-Sat

建矛盾: hate的必须分开,

like的必须栓在同一个点

距离矛盾：① dis1[ i ] + dis1[ j ] > mid

② dis2[ i ] + dis2[ j ] > mid

③ dis1[ i ] + dis2[ j ] + dis > mid

④ dis2[ i ] + dis1[ j ] + dis > mid

记：dis1 表示 cow 到 s1 的距离， dis2 表示 cow 到 s2 的距离， dis 表示 s1 到 s2 的距离。

2762 Going from u to v or from v to u?

解法：强连通+拓扑

强连通缩点，同一分量的不需要考虑了。

不属于同一强连通分支的点就用拓扑排序来判断，如果某次删除点的时候发现两个入度为0的点，则说明这两个点只能由已经被删掉的点到达。

也就是说这两个点互相不可达。所以只要同时出现了多于一个的0入度的点，那么这个图一定是不符合题目要求的，输出"No".

注：用欧拉路径判断是错的，以下数据

5 8
1 2 1 3 1 5 2 4 2 5 3 4 5 3 5 4

2949* Word Rings 差分约束

2983 Is the Information Reliable?

解法：差分约束

P: c<=s[a]-s[b]<=c

V: 1<=s[a]-s[b]

超级源点： addedge( 0 , i , 0 )

注意：不要忘记建超级源点！！！

2987 Firing 最小割(求解正确性??)

3020 Antenna Placement 2分匹配
3041 Asteroids 2分匹配

3072* Robot 最短路

3114 Countries in War 强联通+最短路

3160 Father Christmas flymouse 强联通+最长路
3164 Command Network 最小树形图
3169 Layout 差分约束

3177 Redundant Paths 双联通分量

3189 Steady Cow Assignment 网络流

3204 Ikki's Story I - Road Reconstruction 最大流
3207 Ikki's Story IV - Panda's Trick 2分图
3216 Repairing Company 2分匹配
3228 Gold Transportation 网络流
3255 Roadblocks 最短路
3259 Wormholes 最短路
3268 Silver Cow Party 最短路
3275 Ranking the Cows dfs

3281 Dining 最大流

3308 Paratroopers 最小割
3310 Caterpillar
3311 Hie with the Pie floyd
3328 Cliff Climbing 最短路
3343 Against Mammoths 2分匹配

3352 Road Construction 桥

3439 Server Relocation 最短路

3463 Sightseeing 最短路
3469 Dual Core CPU 最小割

3487 The Stable Marriage Problem 稳定婚姻

3522 Slim Span 最小生成树

3594 Escort of Dr. Who How 最短路

3615 Cow Hurdles 最短路

3623 Wedding 2-sat

3653 Here We Go(relians) Again 最短路
3659* Cell Phone Network 最小支配集
3660 Cow Contest 拓扑
3662* Telephone Lines 最短路
3678 Katu Puzzle 2-sat
3683* Priest John's Busiest Day 2-sat求解
3687 Labeling Balls 差分约束或拓扑
3692 Kindergarten 2分匹配

3694 Network 无向图缩点

3723 *Conscription 最小生成树