python3 联合概率，边缘概率，贝叶斯定理(含详细推导）

最新推荐文章于 2023-11-14 17:45:35 发布

我不爱机器学习

最新推荐文章于 2023-11-14 17:45:35 发布

阅读量5.6k

点赞数 6

分类专栏： python 数据分析

本文链接：https://blog.csdn.net/mengjizhiyou/article/details/103178794

版权

数据分析同时被 2 个专栏收录

25 篇文章 9 订阅

订阅专栏

python

24 篇文章 5 订阅

订阅专栏

1、贝叶斯原理

假设有两个随机变量X；Y（下方左图）； X的取值为 { $x_i$ }，其中 i=1,...,M(M个特征）； Y的取值为 { $y_j$ }，，其中 j=1,...,L（L个类），如下图所示，M=5, L=3。

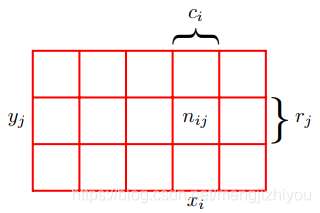
假设这两个变量的实例总数N，那用 $n_{ij}$ 表示 $X=x_i,Y=y_j$ 的实例数，即数组相应单元格 (cell (i,j) ) 中的点数 ,概率形式为 $p(X=x_i,Y=y_j) = \frac{n_{ij}}{N}$ 。

第 i 列对应 $X=x_i$ 的点的个数用 $\large c_i$ 表示，第 j 行对应 $Y=y_j$ 的点的个数用 $\large r_j$ 表示。这里隐式的假设 $N\rightarrow \infty$ 。

同时，不管 Y 的取值是多少，X 的取值概率可以写成 $p(X=x_i)=\frac{c_i}{N}$ ，即由落在第 i 列的点的总数除以所有行所有列的总数。

$c_i$ 是由第 i 列每个单元的实例数的和，因此有 $c_i = \sum _jn_{ij}$ ，

所以有 $p(X=x_i)=\frac{c_i}{N}=\frac{\sum _{j=1}^Ln_{ij}}{N}=\sum _{j=1}^L\frac{n_{ij}}{N} =\sum _{j=1}^Lp(X=x_i,Y=y_j)$ （求和规则）。

假设只考虑 $X=x_i$ 的实例，则在该假设下 $Y=y_j$ 的实例可以写成 $p(Y=y_j|X=x_i)$ 。

则第 i 列中落在cell (i,j) 的实例数的比值为 $p(Y=y_j|X=x_i) =\frac{n_{ij}}{c_i}$ ，

根据以上公式可以推导出 $p(X=x_i,Y=y_j) = \frac{n_{ij}}{N}=\frac{n_{ij}}{c_i}\cdot \frac{c_i}{N} =p(Y=y_j|X=x_i) \cdot p(X=x_i)$ （乘积法则）。

上式中：形如 ${\color{Red} p(X=x_i,Y=y_i)}$ 称为联合概率（joint probability），即包含多个条件且所有条件同时成立的概率，也可记为 $p(x_i,y_i)$ or $p(x_iy_i)$ ；

形如 ${\color{Blue} p(X=x_i)}$ 称为边缘概率（marginal probability），它是通过将其他变量(这里是Y)边缘化或求和得到的，即仅与单个随机变量有关的概率；

形如 ${\color{Purple} p(Y=y_j|X=x_i)}$ 称为条件概率（conditional probability)，即在给定 $X=x_i$ 的条件下 $Y=y_j$ 的概率，也可记为 $p(y_j|x_i)$ 。

由上可得出概率规则（The Rules of Probability）：

sum rule : $p(X)=\sum _{Y}p(X,Y)$

product rule: $p(X,Y) =p(Y|X) p(X)$

根据 product rule，结合对称性 $p(X, Y) = p(Y, X)$ ，得到条件概率之间的关系如下：

$\large {\color{DarkRed} p(Y|X)=\frac{p(X|Y)p(Y)}{p(X)} }$ (式1）

上式即贝叶斯定理 (Bayes’ theorem)，是英国数学家托马斯·贝叶斯提出的。在贝叶斯定理中，通过使用 sum rule 可以得到：

$p(X)=\sum _{Y}p(Y|X) p(Y)$ (式2）

根据上面两式，可以把贝叶斯定理中的分母（式1 ) 看作是保证条件概率的和在等式（式2）左边所需的归一化常数除以所有Y = 1的值。

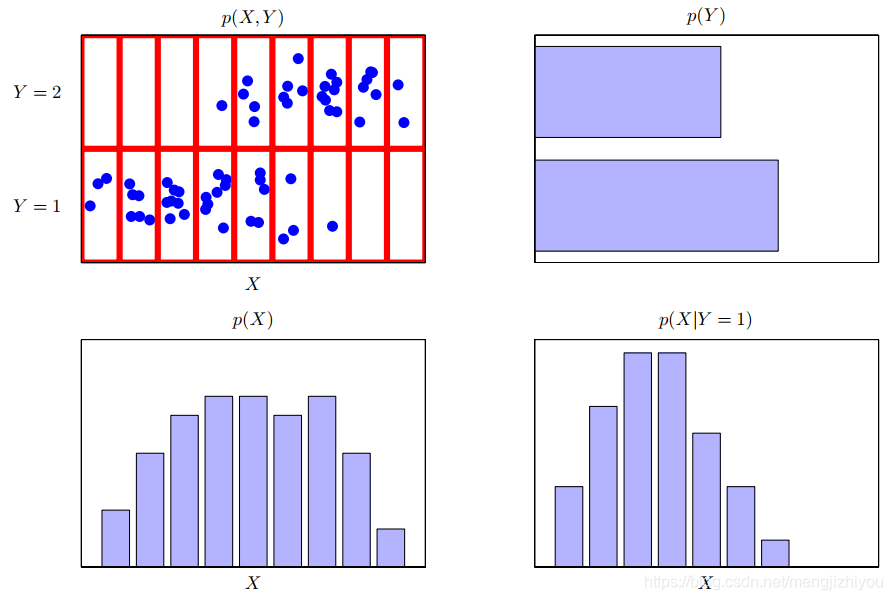
一个关于两个变量的分布的例子，X取9个值，Y取2个值。左下角的图显示了从这些变量的联合概率分布中抽取的60个点（N=60）的样本。剩下的图显示了p(X)和p(Y)的边缘分布的直方图估计值和以及条件分布p(X|Y = 1)对应于右下角的最后一行。

案例：

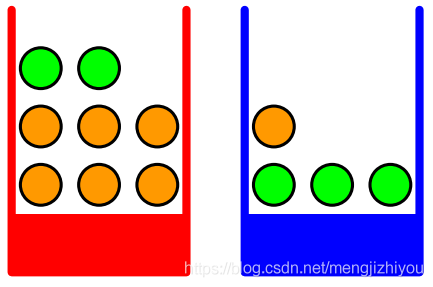
假设有两个盒子 (B)（上方右图），一个红色 (r)，一个蓝色 (b)，两个盒子里分别有苹果 (a) 和橘子 (o)。

分别从两个盒中拿出水果，水果选自红盒的概率4/10，即 $p(B=r)=4/10$ ，水果来自蓝盒的概率为6/10，即 $p(B=b)=6/10$ 。

提问：选择一个苹果的总概率是多少？假设选了一个橙色的橘子，那么选的盒子是蓝色的概率是多少？

将 X 当作盒子（类似属性），Y 当作水果（类似标签）。

由上可知：

将盒子当作一个整体时： $p(B=r)=4/10$

$p(B=b)=6/10$

$p(B=r)+p(B=b)=1$

将红盒子当作一个整体时： $p(F=a|B=r)=1/4$

$p(F=o|B=r)=3/4$

将蓝盒子当作一个整体时： $p(F=a|B=b)=3/4$

$p(F=o|B=b)=1/4$

这些都被归一化（normalized），所以：

$p(F=a|B=r)+p(F=o|B=r)=1$

$p(F=a|B=b)+p(F=o|B=b)=1$

根据sum and product rules 可以计算：

选取苹果的总概率： $p(F=a)=p(F=a,B=r)+p(F=a,B=b)$

$=p(F=a|B=r)p(B=r)+p(F=a|B=b)p(B=b)$

$=1/4*4/10+3/4*6/10=11/20$

根据 sum rule: $p(F=o)=1-p(F=a)=1-11/20=9/20$

假设被告知选中了一个水果，是一个橙子，则它来自哪个盒子的概率是多少？

$p(B=r|F=o)=\frac{p(F=o,B=r)}{p(F=o)}=\frac{p(F=o|B=r)p(B=r)}{p(F=o)}$

$=\frac{3}{4}\times \frac{4}{10}\times \frac{20}{9}=\frac{2}{3}$

根据 sum rule: $p(B=b|F=o)=1-2/3=1/3$

贝叶斯定理的解释：

如果在被告知所选水果的身份(苹果or橘子）之前，被问及选择了哪个盒子，那么所能得到的最完整的信息是概率p(B)，称为先验概率（prior probability），因为它是在观察到水果的身份之前可用的概率。
当知道水果的身份时，可以使用贝叶斯定理计算概率 $p(B|F)$ ，称为后验概率（posterior probability）,因为它是观察F后获得的概率。
在该例中，选择红盒子的先验概率是 4/10，所以更倾向于选择蓝盒子。但是，通过观察选取的水果是橘子时，发现来自红盒子的概率是 2/3，所以更可能选自红盒子。实际中，红盒子中橘子的比例明显比蓝盒子的高，这一证据（evidence）更倾向于红盒子。
如果两个变量（属性/特征）独立，则联合概率是两个变量边缘概率的乘积，即 $p(X,Y)=p(X)p(Y)$ 。则在X的条件下Y独立，根据product rule，得到条件概率 $p(Y|X)=p(Y)$ 。若两个盒子的两种水果占比一样，则 $p(F|B)=P(F)$ , 则苹果与选择的盒子无关。

2、贝叶斯（NB）基本方法

朴素贝叶斯方法是一组基于贝叶斯定理的监督学习算法，其“朴素”假设是给定类变量值的每一对特征之间的条件独立。

根据贝叶斯原理可知先验概率分布： $P(Y=y_j), j=1,2,3,...,L$

条件概率分布为： $P(X=x|Y=y_j)=P(X_1=x_1,...,X_m=x_m|Y=y_j), j=1,2,3,...,L$

条件概率分布 $P(X=x|Y=y_j)$ 有指数级数量的参数，其估计实际是不可行的。假设 $x_i$ 可取值有 $S_i(i=1,2,..,M)$ 个，Y可取值有L个，则参数个数是 $L\prod _{i=1}^MS_i$ 。

贝叶斯对条件概率分布做了条件独立性假设，由于这是一个较强的假设，朴素贝叶斯因此得名。条件独立行假设：

$P(X=x|Y=y_j)=P(X_1=x_1,..,X_n=x_n|Y=y_j)=\prod _{i=1}^{M}P(x_i|y_j)$ (式3)

NB实际上学习到生成数据的机制，属于生成模型。条件独立假设等于是说用于分类的特征在类确定的条件下都是条件独立的。这一假设使NB变得简单，但有时会牺牲一定的分类准确率。

NB在分类时，对给定的输入x,通过学习到的模型计算后验概率分布 $P(Y=y_j|X=x),x=(x_1,x_2,...,x_M)$ ,将后验概率最大的类作为x的类输出。

$P(Y=y_j|X=x) = \frac{P(X=x|Y=y_j)P(Y=y_j)}{P(x_1,x_2,..,x_M)} = \frac{P(X=x|Y=y_j)P(Y=y_j)}{\sum_LP(X=x|Y=y_j)P(Y=y_j)}$ (式4)

将式3带入式4：

$P(Y=y_j|X=x) = \frac{P(Y=y_j)\prod _MP(x_i|y_j)}{P(x_1,x_2,..,x_M)}$

该式是NB分类的基本共识，则NB分类器可表示为：

$y=f(x)=arg \max_{y_j}\frac{P(Y=y_j)\prod _MP(x_i|y_j)}{P(x_1,x_2,..,x_M)}, j=1,2,...,L$

上式中分母 $P(x_1,x_2,..,x_M)$ 对所有 $y_j$ 都相同且是常量,所以，

$P(Y=y_j|x_1,x_2,...,x_M) =P(Y=y_j|X=x) \propto P(Y=y_j)\prod _{i=1}^{M}P(x_i|y_j)$

$\bg_white {\color{Red} P(Y=y_j|x_1,x_2,...,x_M) =arg \max_{y} P(y_j)\prod _{i=1}^{M}P(x_i|y)}$

后验最大化含义：

贝叶斯将实例分到后验概率最大的类中，等价于期望分险最小化。假设有L种可能的类别标记，即 $Y=y_1,y_2,..,y_L$ ， $\lambda_{ij}$ 是将一个真实标记为 $y_j$ 的样本误分类为 $y_i$ 所产生的损失。基于后验概率 $P(y_j|x)$ 可获得奖样本 x 分类为 $y_i$ 所产生的期望损失（expected loss),即在样本 x 上的条件风险（conditional risk）：

$R(y_i|x) = \sum_{j=1}^L\lambda_{ij}P(y_j|x)$

任务是寻找一个判定标准h,最小化总体风险。

$R(h) = E_x[R(h(x)|x)]$

对每个样本x,若h能最小化条件风险 $R(h(x)|x)$ ，则总体风险 $R(h)$ 也将被最小化。这就产生了贝叶斯判定准则（Bayes decision rule)：为最小化总体风险，只需在每个样本上选择那个能使条件风险 $R(y|x)$ 最小的类别标记，即：

$h^*(x) = arg \min_yR(y_i|x)$

$h^*(x)$ 被称为贝叶斯最优分类器（Bayes optimal classifier)，与之对应的总体风险 $R(h^*)$ 称为贝叶斯风险(Bayes risk). $1-R(h^*)$ 反映了分类器所能达到的最好性能，即通过机器学习所能产生的模型精度的理论上线。

若目标是最小化分类错误率，则误判损失 $\lambda_{ij}$ 可写为：

错误率采用0/1损失函数：

$\lambda_{ij}=\left\{\begin{matrix} 0, i=j \\ 1,otherwise \end{matrix}\right.$ $\Rightarrow$ $L(Y,f(X))=\left\{\begin{matrix} 0, Y=f(X) \\ 1,Y\neq f(X) \end{matrix}\right.$

此时条件风险，逐个求解（当 i=j 时，R=0），可得出下式(式中 $i=j$ )：

$R(y_i|x) =arg \min \sum_{j=1}^L\lambda_{ij}P(y_j|x)$

$=arg \min \sum_{j=1}^LP(Y \neq y_j|x)$

$=1-P(y_j|x)$

于是，最小化分类错误率的最优分类器为（根据风险最小化准则就得到了后验概率最大化准则）：

$h^*(x) = arg \max_{y_j\in Y}P(y_j|x)$

后验概率最大等价于 0-1 损失函数时的期望风险最小化。

从贝叶斯判定准则来最小化觉得风险，首先得获得后验概率 $P(y_j|x)$ 。但在现实任务中很难直接获得。所以机器学习是从有限的训练样本里尽可能准确地估计出后验概率 $P(y_j|x)$ 。主要有两种策略：

给定 x,可通过直接建模 $P(y_j|x)$ 来预测 y, 这样得到的模型是判别式模型（决策树、神经网络、SVM）
也可先对联合概率分布 $P(x,y_j)$ ,然后再由此获得 $P(y_j|x)$ ，这样得到生成式模型

这只是从概率角度来理解机器学习，事实上很多机器学习技术无须准确估计出后验概率就能准确进行分类。

3、朴素贝叶斯参数估计

3.1 极大似然估计

最大似然估计 (MLE) 是找到可以最大化可能性的参数，而最大后验估计 (MAPE) 是找到可以最大化后验概率的参数。

在NB中，学习意味着估计 $P(Y=y_j)$ 和 $P(X=x_i|Y=y_j)$ .可以用极大似然估计法估计相应概率。

类先验概率 $P(Y=y_j)$ 表达了样本空间中各类样本所占的比例，根据大数定律，当训练集包含充足的独立同分布样本时， $P(Y=y_j)$ 可通过各类样本出现的频率进行估计。

类条件概率 $\bg_white P(X=x_i|Y=y_j)$ 来说，由于其涉及关于x所有属性的联合概率，无法直接根据样本出现的频率来估计。

估计类条件概率常用策略是先假定其具有某种确定的概率分布形式，再基于训练样本对概率分布的参数进行估计。记类别y的类条件概率为 $\bg_white P(X=x_i|Y=y_j)$ ，假设 $\bg_white P(X=x_i|Y=y_j)$ 具有确定的形式且被参数向量theta 唯一确定，则任务就是利用训练集DF估计参数theta。

假设有N个样本，先验概率 $P(Y=y_j)$ 的极大似然估计：

$P(Y=y_j) = \frac{\sum_{n=1}^NI(y_n=y_j)}{N}$

第i个特征 $x_i$ 的取值集合为{ $S_{i1},S_{i2},...,S_{il}$ }，条件概率 $\bg_white P(X=S_{il}|Y=y_j)$ 的极大似然估计为：

$\bg_white P(X=S_{il}|Y=y_j) =\frac{\sum_{n=1}^NI(x_i=S_{il},y_n=y_j)}{\sum_{n=1}^N I(y_n=y_j)}$ I：指示函数,用于计算个数

3.2 贝叶斯估计

用极大似然估计可能会出现所要估计的概率值为0的情况，这会影响到后验概率的计算结果，使分类产生偏差。解决贝叶斯估计可以解决这一问题。条件概率的贝叶斯估计( $S_i$ 为第 i 特征的取值个数）：

$\bg_white P(X=S_{il}|Y=y_j) =\frac{\sum_{n=1}^NI(x_i=S_{il},y_n=y_j)+\lambda}{\sum_{n=1}^N I(y_n=y_j)+S_i\lambda}$

lambda>0,等价于在随机变量各个取值的频数上赋予一个整数；lambda=0，极大似然估计；lambda=1,拉普拉斯平滑。对任何 $l =1,2,..,S_i,j=1,2,..,L$ ,有：

$P_\lambda(x_i=a_{il}|Y=y_j)>0$

$\sum_{l=1}^{S_i}P(x_i=a_{il}|Y=y_j)=1$

先验概率贝叶斯的估计是：

$P_\lambda(Y=y_j)=\frac{\sum_{n=1}^NI(y_n=y_j)+\lambda}{N+L\lambda}$ (N为样本数，L为类别数）

贝叶斯优点：

分类容易且快速，而且在多类预测中表现良好
当条件独立假设成立时分类比其他模型比如对率分类性能更好，而且也需要更少的训练数据
最后一个优点也是它的缺点，就是独立的预测变量的假设。因为在现实生活中几乎不可能获得一组完全独立的预测变量。

4、贝叶斯类型

4.1 伯努利贝叶斯（ Bernoulli Naive Bayes）

用于对多元伯努利分布的数据进行训练和分类。数据可以有多个特征，但每个特征都被假定为二值变量即取值为0，1（boolean),因此该类要求样本用二值特征向量表示。X的取值均为0，1，Y可取其他值。
决策规则： $P(x_i|y)=P(i|y)x_i+(1-P(i|y))(1-x_i)$
与多项式NB规则的不同之处在于它显式地惩罚作为类指标的特征的不出现，而多项式变量会简单地忽略一个不出现的特征
在文本分类的情况下，可以使用单词出现向量(而不是单词计数向量)来训练和使用这个分类器。BernoulliNB可能在某些数据集上表现得更好，特别是那些文档更短的数据集。如果时间允许，最好对两个模型都进行评估。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_circles
from sklearn.naive_bayes import BernoulliNB
from sklearn.ensemble import RandomTreesEmbedding

# make a synthetic dataset
X, y = make_circles(factor=0.5, random_state=0, noise=0.05)

# use RandomTreesEmbedding to transform data
hasher = RandomTreesEmbedding(n_estimators=10, random_state=0, max_depth=3)
X_transformed = hasher.fit_transform(X)

# learn a navie bayes classifier on the transformed data
nb = BernoulliNB()
nb.fit(X_transformed, y)

# scatter plot of original and reduced data
fig = plt.plot(figsize=(8, 4))

ax = plt.subplot(121)
ax.scatter(X[:, 0], X[:, 1], c=y, s=50, edgecolor='k')
ax.set_title('Original Data(2d)')
ax.set_xticks(())
ax.set_yticks(())

# Plot the decision in original space. For that, we will assign a color
# to each point in the mesh [x_min, x_max]x[y_min, y_max].
h = .01
x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))

# transform grid using RandomTreesEmbedding
transformed_grid = hasher.transform(np.c_[xx.ravel(), yy.ravel()])
y_grid_pred = nb.predict_proba(transformed_grid)[:, 1]

ax = plt.subplot(122)
ax.set_title('Navie Bayes on Transformed data')
ax.pcolormesh(xx, yy, y_grid_pred.reshape(xx.shape))
ax.scatter(X[:, 0], X[:, 1], c=y, s=50, edgecolor='k')
ax.set_ylim(-1.4, 1.4)
ax.set_xlim(-1.4, 1.4)
ax.set_xticks(())
ax.set_yticks(())

4.2 多项式贝叶斯 (Multinomial Naive Bayes)

用于对多项分布的数据进行训练和分类。数据可以有多个特征。可用来过滤垃圾邮件。
决策规则（由最大似然的平滑估计）： $P(Y=y_j)=\frac{\sum_{n=1}^NI(y_n=y_j)+\alpha}{N+L\alpha}$ (N为样本数，L为类别数）,平滑的先验 alpha≥0，解释学习样本中不存在的特征，并防止在进一步的计算中出现零概率；alpha=1，叫Laplace平滑；alpha<1 时，叫Lidstone平滑。

import numpy as np
X = np.random.randint(5, size=(6, 100))
y = np.array([1, 2, 3, 4, 5, 6])
from sklearn.naive_bayes import MultinomialNB
clf = MultinomialNB()
clf.fit(X, y)
# MultinomialNB(alpha=1.0, class_prior=None, fit_prior=True)
print(clf.predict(X[2:3]))
# [3]

4.3 补充贝叶斯 (Complement Naive Bayes)

CNB是标准多项式朴素贝叶斯(MNB)算法的一种改进，尤其适用于类别不平衡数据集
CNB使用来自每个类的补数的统计数据来计算模型的权重
CNB的发明人经验表明，CNB的参数估计比MNB的参数估计更稳定
在文本分类任务上，CNB通常比MNB表现更好(通常有相当大的优势)

4.4 高斯贝叶斯（Gaussian Naive Bayes）

用于对高斯分布的数据进行训练和分类，特征是连续值。
判别规则：

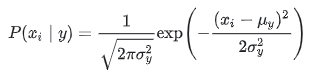
class NavieBayes:
    def __init__(self):
        self.model = None

    @staticmethod
    def mean(x):
        return sum(x) / float(len(x))

    def stdev(self, x):
        avg = self.mean(x)
        variance = sum([(x - avg) ** 2 for x in x]) / float(len(x) - 1)
        return math.sqrt(variance)

    def gaussian_probability(self, x, mean, stdev):
        exponent = math.exp(-1 / 2 * ((x - mean) / stdev) ** 2)
        return 1 / math.sqrt(2 * math.pi * (stdev ** 2)) * exponent

    def summarize(self, train_data):
        # 对每个特征求平均和标准误差
        summaries = [(self.mean(column), self.stdev(column)) for column in zip(*train_data)]
        return summaries

    def fit(self, X, y):
        labels = list(set(y))
        data = {label: [] for label in labels}
        for r, label in zip(X, y):
            data[label].append(r)
        self.model = {label: self.summarize(value) for label, value in data.items()}
        return 'gaussianNB train done!'

    def calculate_probabilities(self, input_data):
        # 计算每个类的特征的概率
        # summaries:{0.0: [(5.0, 0.37),(3.42, 0.40)], 1.0: [(5.8, 0.449),(2.7, 0.27)]}
        # input_data:[1.1, 2.2]
        probabilities = {}
        for label, value in self.model.items():
            probabilities[label] = 1
            for i in range(len(value)):
                mean, stdev = value[i]
                probabilities[label] *= self.gaussian_probability(input_data[i], mean, stdev)
                # 这一步看上面的大红色公式
                # P(class|data) = P(X|class) * P(class), simplified
                # P(class=0|X1,X2) = P(X1|class=0) * P(X2|class=0) * P(class=0)
        return probabilities

    def predict(self, X_test):
        # 单个数据
        # # {0.0: 2.9680340789325763e-27, 1.0: 3.5749783019849535e-26}
        label= sorted(self.calculate_probabilities(X_test).items(), key=lambda x: x[-1])[-1][0]
        return label

    def score(self, X_test, y_test):
        right = 0
        for X, y in zip(X_test, y_test):
            label = self.predict(X)
            if label == y:
                right += 1
        return right / float(len(X_test))
    
    # 预测多个数据
    # def predict(self, X_test):
    #     # # {0.0: 2.9680340789325763e-27, 1.0: 3.5749783019849535e-26}
    #     label = []
    #     for x in X_test:
    #         label.append(sorted(self.calculate_probabilities(x).items(), key=lambda x: x[-1])[-1][0])
    #     return label
    #
    # def score(self, X_test, y_test):
    #     label = self.predict(X_test)
    #     acc = sum(label == y_test)/float(len(X_test))
    #     return acc
    # model.predict([[4.4, 3.2, 1.3, 0.2]]),单个数据为二维数据


from sklearn import datasets
from sklearn.model_selection import train_test_split
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import math

# prepare the data
iris = datasets.load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['label'] = iris.target.astype(int)
df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
data = df.values[:100]
X, y = data[:100, :-1], data[:100, -1].astype(int)
X_train, X_test, y_train, y_test = train_test_split(X, y)

model = NavieBayes()
model.fit(X_train, y_train)
print(model.predict([4.4, 3.2, 1.3, 0.2])) # 0
model.score(X_test, y_test) # 1.0

# 对比
from sklearn.naive_bayes import GaussianNB

clf = GaussianNB()
clf.fit(X_train, y_train)
clf.predict([[4.4, 3.2, 1.3, 0.2]])
# array([0])
clf.score(X_test, y_test)
# 1.0

4.5 核外贝叶斯（Out-of-core naive Bayes）

可以用来处理大规模的分类问题，对于这些问题，整个训练集可能不适合在内存中。

参考：

https://blog.csdn.net/tick_tock97/article/details/79885868

《机器学习》-周志华

《统计学习方法》-李航

我不爱机器学习

关注

6
点赞
踩
33

收藏

觉得还不错? 一键收藏
4
评论
python3 联合概率，边缘概率，贝叶斯定理(含详细推导）

1、贝叶斯原理假设有两个随机变量X；Y（下方左图）； X的取值为 {}，其中 i=1,...,M(M个特征）； Y的取值为 {}，，其中 j=1,...,L（L个类），如下图所示，M=5, L=3。假设这两个变量的实例总数N，那用表示的实例数，即数组相应...
复制链接

扫一扫