面试整理：关于代价函数，正则化

 向AI转型的程序员都关注了这个号???

大数据挖掘DT数据分析  公众号： datadw

注：代价函数（有的地方也叫损失函数，Loss Function）在机器学习中的每一种算法中都很重要，因为训练模型的过程就是优化代价函数的过程，代价函数对每个参数的偏导数就是梯度下降中提到的梯度，防止过拟合时添加的正则化项也是加在代价函数后面的。在学习相关算法的过程中，对代价函数的理解也在不断的加深，在此做一个小结。

 

1. 什么是代价函数？

---

假设有训练样本(x, y)，模型为h，参数为θ。h(θ) = θ^Tx（θ^T表示θ的转置）。

（1）概况来讲，任何能够衡量模型预测出来的值h(θ)与真实值y之间的差异的函数都可以叫做代价函数C(θ)，如果有多个样本，则可以将所有代价函数的取值求均值，记做J(θ)。因此很容易就可以得出以下关于代价函数的性质：

• 对于每种算法来说，代价函数不是唯一的；

• 代价函数是参数θ的函数；

• 总的代价函数J(θ)可以用来评价模型的好坏，代价函数越小说明模型和参数越符合训练样本(x, y)；

• J(θ)是一个标量；

（2）当我们确定了模型h，后面做的所有事情就是训练模型的参数θ。那么什么时候模型的训练才能结束呢？这时候也涉及到代价函数，由于代价函数是用来衡量模型好坏的，我们的目标当然是得到最好的模型（也就是最符合训练样本(x, y)的模型）。因此训练参数的过程就是不断改变θ，从而得到更小的J(θ)的过程。理想情况下，当我们取到代价函数J的最小值时，就得到了最优的参数θ，记为：

例如，J(θ) = 0，表示我们的模型完美的拟合了观察的数据，没有任何误差。

（3）在优化参数θ的过程中，最常用的方法是梯度下降，这里的梯度就是代价函数J(θ)对θ₁, θ₂, ..., θ_n的偏导数。由于需要求偏导，我们可以得到另一个关于代价函数的性质：

• 选择代价函数时，最好挑选对参数θ可微的函数（全微分存在，偏导数一定存在）

 

2. 代价函数的常见形式

---

经过上面的描述，一个好的代价函数需要满足两个最基本的要求：能够评价模型的准确性，对参数θ可微。 

 

2.1 均方误差

在线性回归中，最常用的是均方误差(Mean squared error)，具体形式为：

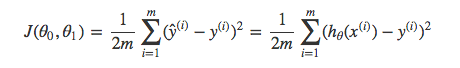
m：训练样本的个数；

h_θ(x)：用参数θ和x预测出来的y值；

y：原训练样本中的y值，也就是标准答案

上角标(i)：第i个样本

 

2.2 交叉熵

在逻辑回归中，最常用的是代价函数是交叉熵(Cross Entropy)，交叉熵是一个常见的代价函数，在神经网络中也会用到。下面是《神经网络与深度学习》一书对交叉熵的解释：

交叉熵是对「出乎意料」（译者注：原文使用suprise）的度量。神经元的目标是去计算函数y, 且y=y(x)。但是我们让它取而代之计算函数a, 且a=a(x)。假设我们把a当作y等于1的概率，1−a是y等于0的概率。那么，交叉熵衡量的是我们在知道y的真实值时的平均「出乎意料」程度。当输出是我们期望的值，我们的「出乎意料」程度比较低；当输出不是我们期望的，我们的「出乎意料」程度就比较高。

 

在1948年，克劳德·艾尔伍德·香农将热力学的熵，引入到信息论，因此它又被称为香农熵(Shannon Entropy)，它是香农信息量(Shannon Information Content, SIC)的期望。香农信息量用来度量不确定性的大小：一个事件的香农信息量等于0，表示该事件的发生不会给我们提供任何新的信息，例如确定性的事件，发生的概率是1，发生了也不会引起任何惊讶；当不可能事件发生时，香农信息量为无穷大，这表示给我们提供了无穷多的新信息，并且使我们无限的惊讶。

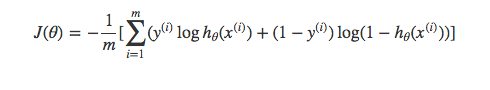
符号说明同上 

 

2.3 神经网络中的代价函数

学习过神经网络后，发现逻辑回归其实是神经网络的一种特例（没有隐藏层的神经网络）。因此神经网络中的代价函数与逻辑回归中的代价函数非常相似：

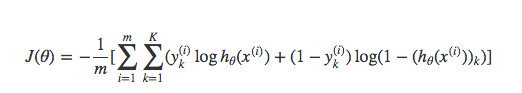
这里之所以多了一层求和项，是因为神经网络的输出一般都不是单一的值，K表示在多分类中的类型数。

例如在数字识别中，K=10，表示分了10类。此时对于某一个样本来说，输出的结果如下：

  1.1266e-004
  1.7413e-003
  2.5270e-003
  1.8403e-005
  9.3626e-003
  3.9927e-003
  5.5152e-003
  4.0147e-004
  6.4807e-003
  9.9573e-001

一个10维的列向量，预测的结果表示输入的数字是0~9中的某一个的概率，概率最大的就被当做是预测结果。例如上面的预测结果是9。理想情况下的预测结果应该如下（9的概率是1，其他都是0）：

   0
   0
   0
   0
   0
   0
   0
   0
   0
   1

比较预测结果和理想情况下的结果，可以看到这两个向量的对应元素之间都存在差异，共有10组，这里的10就表示代价函数里的K，相当于把每一种类型的差异都累加起来了。

 

3. 代价函数与参数

---

代价函数衡量的是模型预测值h(θ) 与标准答案y之间的差异，所以总的代价函数J是h(θ)和y的函数，即J=f(h(θ), y)。又因为y都是训练样本中给定的，h(θ)由θ决定，所以，最终还是模型参数θ的改变导致了J的改变。对于不同的θ，对应不同的预测值h(θ)，也就对应着不同的代价函数J的取值。变化过程为：

θ−−>h(θ)−−>J(θ)

θ引起了h(θ)的改变，进而改变了J(θ)的取值。为了更直观的看到参数对代价函数的影响，举个简单的例子：

有训练样本{(0, 0), (1, 1), (2, 2), (4, 4)}，即4对训练样本，每个样本对中第1个数表示x的值，第2个数表示y的值。这几个点很明显都是y=x这条直线上的点。如下图：

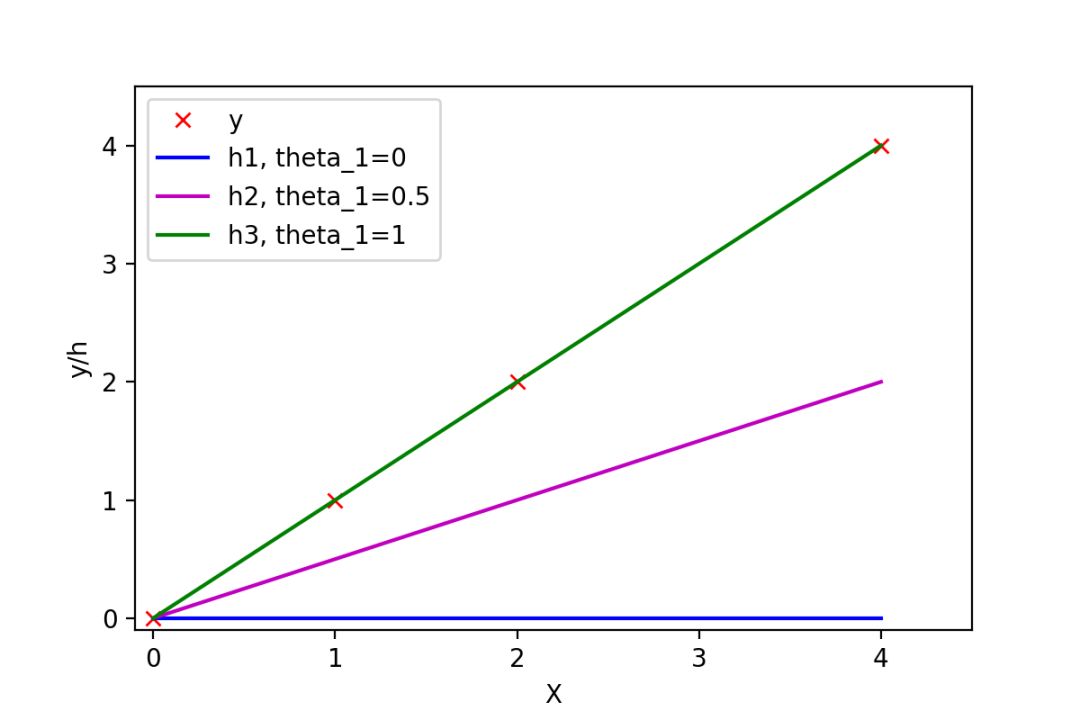
不同参数可以拟合出不同的直线

常数项为0，所以可以取θ₀=0，然后取不同的θ₁，可以得到不同的拟合直线。当θ₁=0时，拟合的直线是y=0，即蓝色线段，此时距离样本点最远，代价函数的值（误差）也最大；当θ₁=1时，拟合的直线是y=x，即绿色线段，此时拟合的直线经过每一个样本点，代价函数的值为0。

通过下图可以查看随着θ₁的变化，J(θ)的变化情况：

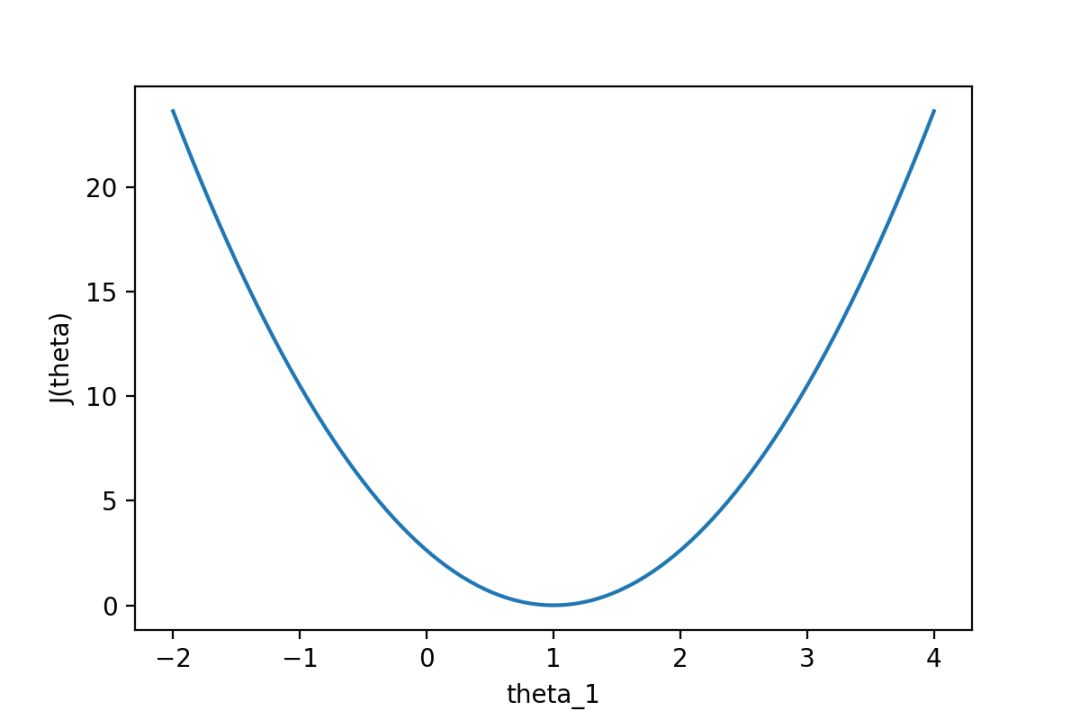
图2：代价函数J(θ)随参数的变化而变化

从图中可以很直观的看到θ对代价函数的影响，当θ₁=1时，代价函数J(θ)取到最小值。因为线性回归模型的代价函数（均方误差）的性质非常好，因此也可以直接使用代数的方法，求J(θ)的一阶导数为0的点，就可以直接求出最优的θ值（正规方程法）。

 

4. 代价函数与梯度

---

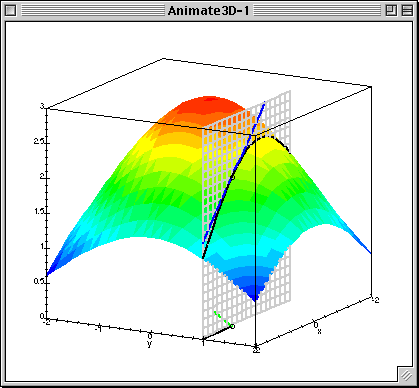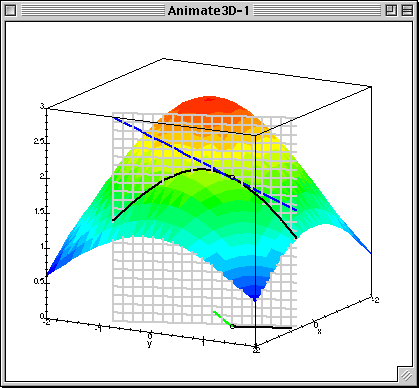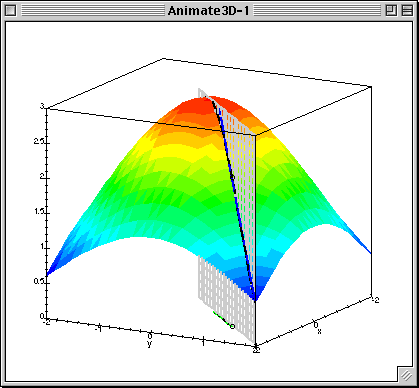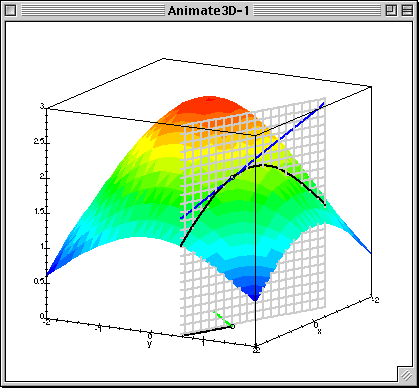
 梯度下降中的梯度指的是代价函数对各个参数的偏导数，偏导数的方向决定了在学习过程中参数下降的方向，学习率（通常用α表示）决定了每步变化的步长，有了导数和学习率就可以使用梯度下降算法（Gradient Descent Algorithm）更新参数了。下图中展示了只有两个参数的模型运用梯度下降算法的过程。

下图可以看做是代价函数J(θ)与参数θ做出的图，曲面上的一个点(θ₀, θ₁, J(θ))，有无数条切线，在这些切线中与x-y平面(底面，相当于θ₀, θ₁)夹角最大的那条切线就是该点梯度的方向，沿该方向移动，会产生最大的高度变化(相对于z轴，这里的z轴相当于代价函数J(θ))。

正则化（Regularization）

1. The Problem of Overfitting

1

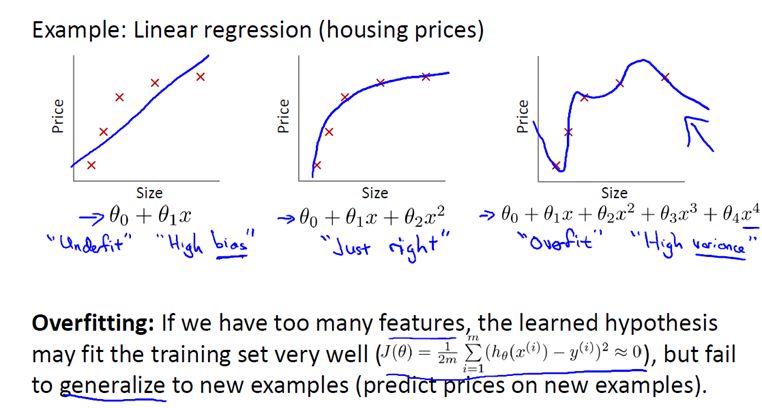
还是来看预测房价的这个例子，我们先对该数据做线性回归，也就是左边第一张图。

如果这么做，我们可以获得拟合数据的这样一条直线，但是，实际上这并不是一个很好的模型。我们看看这些数据，很明显，随着房子面积增大，住房价格的变化趋于稳定或者说越往右越平缓。因此线性回归并没有很好拟合训练数据。

我们把此类情况称为欠拟合(underfitting)，或者叫作叫做高偏差(bias)。

这两种说法大致相似，都表示没有很好地拟合训练数据。高偏差这个词是 machine learning 的研究初期传下来的一个专业名词，具体到这个问题，意思就是说如果用线性回归这个算法去拟合训练数据，那么该算法实际上会产生一个非常大的偏差或者说存在一个很强的偏见。

第二幅图，我们在中间加入一个二次项，也就是说对于这幅数据我们用二次函数去拟合。自然，可以拟合出一条曲线，事实也证明这个拟合效果很好。

另一个极端情况是，如果在第三幅图中对于该数据集用一个四次多项式来拟合。因此在这里我们有五个参数θ₀到θ_4，这样我们同样可以拟合一条曲线，通过我们的五个训练样本，我们可以得到如右图的一条曲线。

一方面，我们似乎对训练数据做了一个很好的拟合，因为这条曲线通过了所有的训练实例。但是，这实际上是一条很扭曲的曲线，它不停上下波动。因此，事实上我们并不认为它是一个预测房价的好模型。

所以，我们把这类情况叫做过拟合(overfitting)，也叫高方差(variance)。

与高偏差一样，高方差同样也是一个历史上的叫法。从第一印象上来说，如果我们拟合一个高阶多项式，那么这个函数能很好的拟合训练集（能拟合几乎所有的训练数据），但这也就面临函数可能太过庞大的问题，变量太多。

同时如果我们没有足够的数据集（训练集）去约束这个变量过多的模型，那么就会发生过拟合。

2

过度拟合的问题通常发生在变量（特征）过多的时候。这种情况下训练出的方程总是能很好的拟合训练数据，也就是说，我们的代价函数可能非常接近于 0 或者就为 0。

但是，这样的曲线千方百计的去拟合训练数据，这样会导致它无法泛化到新的数据样本中，以至于无法预测新样本价格。在这里，术语"泛化"指的是一个假设模型能够应用到新样本的能力。新样本数据是指没有出现在训练集中的数据。

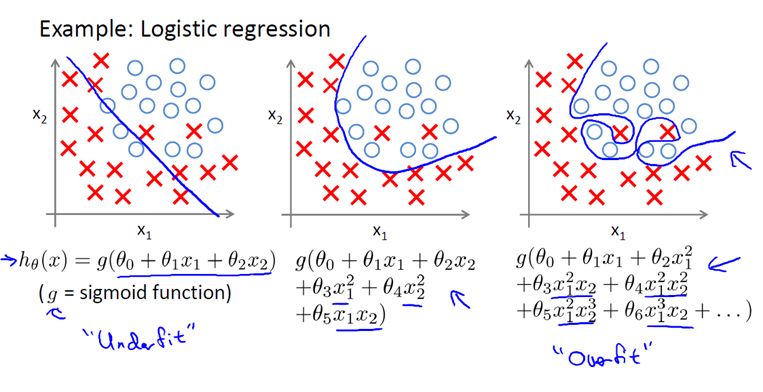
之前，我们看到了线性回归情况下的过拟合。类似的情况也适用于逻辑回归。

3

那么，如果发生了过拟合问题，我们应该如何处理？

过多的变量（特征），同时只有非常少的训练数据，会导致出现过度拟合的问题。因此为了解决过度拟合，有以下两个办法。

方法一：尽量减少选取变量的数量

具体而言，我们可以人工检查每一项变量，并以此来确定哪些变量更为重要，然后，保留那些更为重要的特征变量。至于，哪些变量应该舍弃，我们以后在讨论，这会涉及到模型选择算法，这种算法是可以自动选择采用哪些特征变量，自动舍弃不需要的变量。这类做法非常有效，但是其缺点是当你舍弃一部分特征变量时，你也舍弃了问题中的一些信息。例如，也许所有的特征变量对于预测房价都是有用的，我们实际上并不想舍弃一些信息或者说舍弃这些特征变量。

方法二：正则化

正则化中我们将保留所有的特征变量，但是会减小特征变量的数量级（参数数值的大小θ(j)）。

这个方法非常有效，当我们有很多特征变量时，其中每一个变量都能对预测产生一点影响。正如我们在房价预测的例子中看到的那样，我们可以有很多特征变量，其中每一个变量都是有用的，因此我们不希望把它们删掉，这就导致了正则化概念的发生。

接下来我们会讨论怎样应用正则化和什么叫做正则化均值，然后将开始讨论怎样使用正则化来使学习算法正常工作，并避免过拟合。

2. Cost Function

1

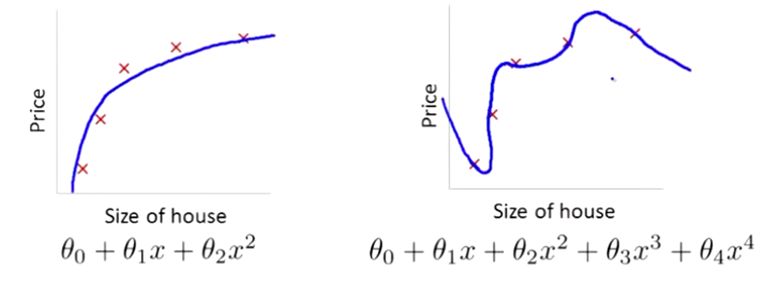
在前面的介绍中，我们看到了如果用一个二次函数来拟合这些数据，那么它给了我们一个对数据很好的拟合。然而，如果我们用一个更高次的多项式去拟合，最终我们可能会得到一个曲线，它能很好地拟合训练集，但却并不是一个好的结果，因为它过度拟合了数据，因此，一般性并不是很好。

让我们考虑下面的假设，我们想要加上惩罚项，从而使参数 θ₃ 和 θ₄ 足够的小。

这里我的意思就是，上图的式子是我们的优化目标，也就是说我们需要尽量减少代价函数的均方误差。

对于这个函数我们对它添加一些项，加上 1000 乘以 θ₃ 的平方，再加上 1000 乘以 θ₄ 的平方，

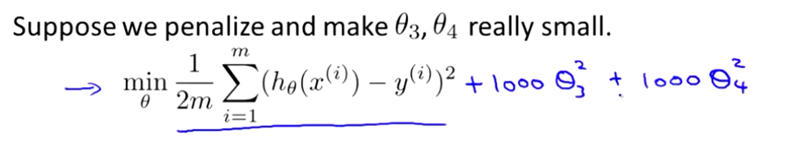
1000 只是我随便写的某个较大的数字而已。现在，如果我们要最小化这个函数，那么为了最小化这个新的代价函数，我们要让 θ₃ 和 θ₄ 尽可能小。因为，如果你在原有代价函数的基础上加上 1000 乘以 θ₃ 这一项 ，那么这个新的代价函数将变得很大，所以，当我们最小化这个新的代价函数时， 我们将使 θ₃ 的值接近于 0，同样 θ₄ 的值也接近于 0，就像我们忽略了这两个值一样。如果我们做到这一点（ θ₃ 和 θ₄ 接近 0 ），那么我们将得到一个近似的二次函数。

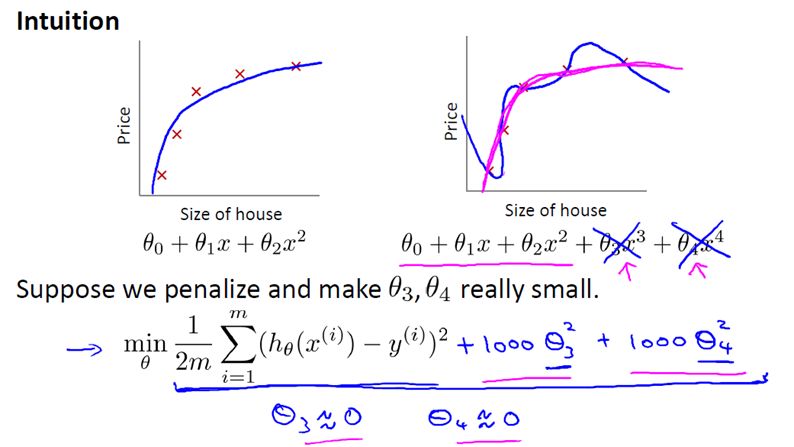
因此，我们最终恰当地拟合了数据，我们所使用的正是二次函数加上一些非常小，贡献很小项（因为这些项的 θ₃、 θ₄ 非常接近于0）。显然，这是一个更好的假设。

2

更一般地，这里给出了正规化背后的思路。这种思路就是，如果我们的参数值对应一个较小值的话（参数值比较小），那么往往我们会得到一个形式更简单的假设。

在我们上面的例子中，我们惩罚的只是 θ₃ 和 θ_{4 ，}使这两个值均接近于零，从而我们得到了一个更简单的假设，实际上这个假设大抵上是一个二次函数。

但更一般地说，如果我们像惩罚 θ₃ 和 θ₄ 这样惩罚其它参数，那么我们往往可以得到一个相对较为简单的假设。

实际上，这些参数的值越小，通常对应于越光滑的函数，也就是更加简单的函数。因此 就不易发生过拟合的问题。

我知道，为什么越小的参数对应于一个相对较为简单的假设，对你来说现在不一定完全理解，但是在上面的例子中使 θ₃ 和 θ₄ 很小，并且这样做能给我们一个更加简单的假设，这个例子至少给了我们一些直观感受。

来让我们看看具体的例子，对于房屋价格预测我们可能有上百种特征，与刚刚所讲的多项式例子不同，我们并不知道 θ₃ 和 θ₄ 是高阶多项式的项。所以，如果我们有一百个特征，我们并不知道如何选择关联度更好的参数，如何缩小参数的数目等等。

因此在正则化里，我们要做的事情，就是把减小我们的代价函数（例子中是线性回归的代价函数）所有的参数值，因为我们并不知道是哪一个或哪几个要去缩小。

因此，我们需要修改代价函数，在这后面添加一项，就像我们在方括号里的这项。当我们添加一个额外的正则化项的时候，我们收缩了每个参数。

顺便说一下，按照惯例，我们没有去惩罚 θ₀，因此 θ₀ 的值是大的。这就是一个约定从 1 到 n 的求和，而不是从 0 到 n 的求和。但其实在实践中
这只会有非常小的差异，无论你是否包括这 θ₀ 这项。但是按照惯例，通常情况下我们还是只从 θ₁ 到 θ_n 进行正则化。

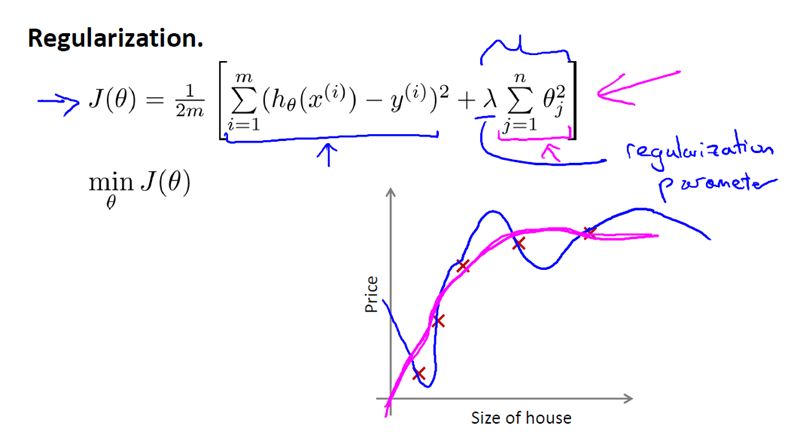
下面的这项就是一个正则化项

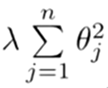
并且 λ 在这里我们称做正则化参数。

λ 要做的就是控制在两个不同的目标中的平衡关系。

第一个目标就是我们想要训练，使假设更好地拟合训练数据。我们希望假设能够很好的适应训练集。

而第二个目标是我们想要保持参数值较小。（通过正则化项）

而 λ 这个正则化参数需要控制的是这两者之间的平衡，即平衡拟合训练的目标和保持参数值较小的目标。从而来保持假设的形式相对简单，来避免过度的拟合。

对于我们的房屋价格预测来说，我们之前所用的非常高的高阶多项式来拟合，我们将会得到一个非常弯曲和复杂的曲线函数，现在我们只需要使用正则化目标的方法，那么你就可以得到一个更加合适的曲线，但这个曲线不是一个真正的二次函数，而是更加的流畅和简单的一个曲线。这样就得到了对于这个数据更好的假设。

再一次说明下，这部分内容的确有些难以明白，为什么加上参数的影响可以具有这种效果？但如果你亲自实现了正规化，你将能够看到这种影响的最直观的感受。

3

在正则化线性回归中，如果正则化参数值 λ 被设定为非常大，那么将会发生什么呢？

我们将会非常大地惩罚参数θ₁ θ₂ θ₃ θ₄ … 也就是说，我们最终惩罚θ₁ θ₂ θ₃ θ₄ …  在一个非常大的程度，那么我们会使所有这些参数接近于零。

如果我们这么做，那么就是我们的假设中相当于去掉了这些项，并且使我们只是留下了一个简单的假设，这个假设只能表明房屋价格等于 θ₀ 的值，那就是类似于拟合了一条水平直线，对于数据来说这就是一个欠拟合 (underfitting)。这种情况下这一假设它是条失败的直线，对于训练集来说这只是一条平滑直线，它没有任何趋势，它不会去趋向大部分训练样本的任何值。

这句话的另一种方式来表达就是这种假设有过于强烈的"偏见" 或者过高的偏差 (bais)，认为预测的价格只是等于 θ₀ 。对于数据来说这只是一条水平线。

因此，为了使正则化运作良好，我们应当注意一些方面，应该去选择一个不错的正则化参数 λ 。当我们以后讲到多重选择时我们将讨论一种方法来自动选择正则化参数 λ  ，为了使用正则化，接下来我们将把这些概念应用到到线性回归和逻辑回归中去，那么我们就可以让他们避免过度拟合了。

3. Regularized Linear Regression

之前我们已经介绍过，岭回归的代价函数如下：

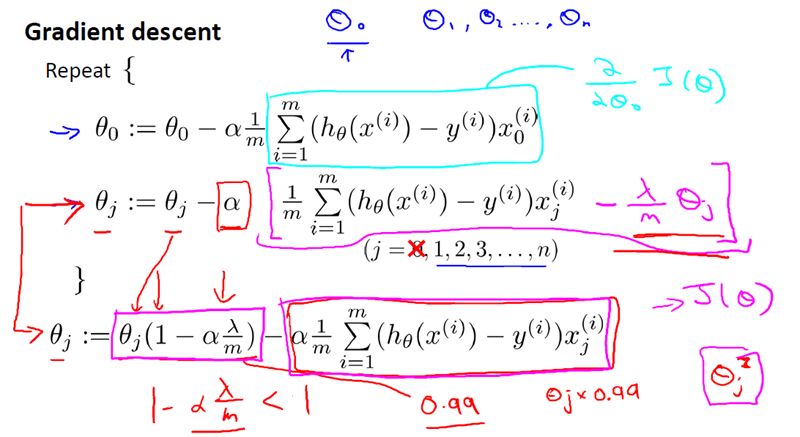
对于线性回归(的求解)，我们之前运用了两种学习算法，一种基于梯度下降，一种基于正规方程。

1

梯度下降，如下：

2

正规方程，如下：

3

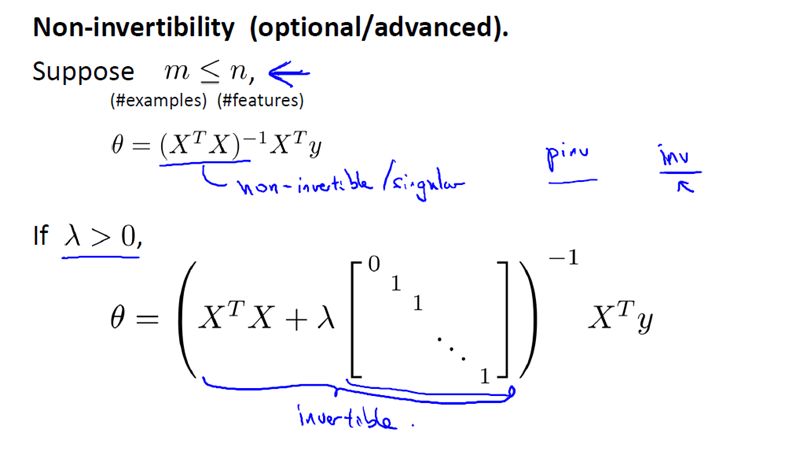
现在考虑 M（即样本量）， 比 N（即特征的数量）小或等于N。

通过之前的博文，我们知道如果你只有较少的样本，导致特征数量大于样本数量，那么矩阵 X^TX 将是不可逆矩阵或奇异（singluar）矩阵，或者用另一种说法是这个矩阵是退化（degenerate）的，那么我们就没有办法使用正规方程来求出 θ 。

幸运的是，正规化也为我们解决了这个问题，具体的说只要正则参数是严格大于零，实际上，可以证明如下矩阵：

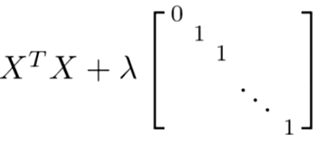
将是可逆的。因此，使用正则还可以照顾任何 X^TX 不可逆的问题。

所以，你现在知道如何实现岭回归，利用它，你就可以避免过度拟合，即使你在一个相对较小的训练集里有很多特征。这应该可以让你在很多问题上更好的运用线性回归。

在接下来的视频中，我们将把这种正则化的想法应用到 Logistic 回归，这样我们就可以让 logistic 回归也避免过度拟合，从而表现的更好。

4. Regularized Logistic Regression

Regularized Logistic Regression 实际上与 Regularized Linear Regression 是十分相似的。

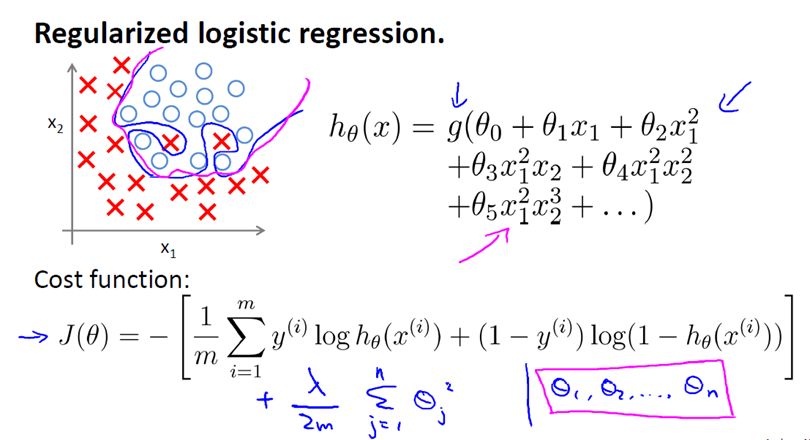
同样使用梯度下降：

如果在高级优化算法中，使用正则化技术的话，那么对于这类算法我们需要自己定义costFunction。

For those methods what we needed to do was to define the function that's called the cost function.

这个我们自定义的 costFunction 的输入为向量 θ ，返回值有两项，分别是代价函数 jVal 以及 梯度gradient。

总之我们需要的就是这个自定义函数costFunction，针对Octave而言，我们可以将这个函数作为参数传入到 fminunc 系统函数中（fminunc 用来求函数的最小值，将@costFunction作为参数代进去，注意 @costFunction 类似于C语言中的函数指针），fminunc返回的是函数 costFunction 在无约束条件下的最小值，即我们提供的代价函数 jVal 的最小值，当然也会返回向量 θ 的解。

上述方法显然对正则化逻辑回归是适用的。

5. 尾声

通过最近的几篇文章，我们不难发现，无论是线性回归问题还是逻辑回归问题都可以通过构造多项式来解决。但是，你将逐渐发现其实还有更为强大的非线性分类器可以用来解决多项式回归问题。下篇文章中，我们将会讨论。

人工智能大数据与深度学习

搜索添加微信公众号：weic2c

长按图片，识别二维码，点关注

---

大数据挖掘DT数据分析

搜索添加微信公众号：datadw

教你机器学习，教你数据挖掘

长按图片，识别二维码，点关注