左式堆

1 相关定义

1.1 零路径长度定义：

到没有两个儿子的节点最短距离， 即零路径长Npl 定义为 从 X 到一个没有两个儿子的 节点的最短路径的长；也即， 非叶子节点到叶子节点的最少边数，其中NULL的零路径长为-1， 叶子节点的零路径长为0；
（零路径长的定义—— 非叶子节点到叶子节点的最少边数，非常重要，因为左式堆的定义是基于零路径长的定义的）

1.２ 左式堆定义：

一棵具有堆序性质的二叉树 ＋ 零路径长：左儿子 ≧ 右儿子　＋　父节点 = min{儿子} +1；
（干货——左式堆的定义是建立在具有堆序性的二叉树上，而不是二叉堆上）

2 merge操作原则：

根值大的堆与根值小的堆的右子堆合并；（干货——merge操作原则）

3 merge操作存在的三种情况（设堆H1的根值小于H2）

• case1） H1只有一个节点；
• case2） H1根无右孩子；
• case3） H1根有右孩子；

补充（Complementary）：左式堆合并操作详解（merge）

左式堆合并原则：大根堆H2与小根堆H1的右子堆合并 （干货——左式堆合并原则）
具体分三种情况（设堆H1的根值小于H2）

• case1）H1只有一个节点（只有它自己而已）： H1只有一个节点，若出现不满足 零路径长：左儿子≧右儿子，交换左右孩子；
  
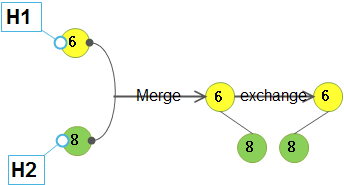
  注 ：上例中（中间所示堆），左儿子的零路径长为-1， 而右儿子的零路径长为0，所以不满足左式堆的条件， 需要交换左右孩子；
• case2）H1根无右孩子： H1根无右孩子，若出现不满足：零路径长：左儿子≧右儿子，需要交换左右孩子。
  
  注：上例中（中间所示堆），左儿子的零路径长为0， 而右儿子的零路径长为1，所以不满足左式堆的条件，需要交换；
• case3）H1根有右孩子：
  • step1）截取H1的右子堆R1， 和截取H2的右子堆R2；
  • step2）将R1 与 R2进行merge操作得到H3， 且取R1和R2中较小根作为新根； （Attention： 现在你将看到，截取后的H1 和 H2， 以及新生成的H3 都是 case2）；
  • step3）比较H3的左右孩子，是否满足左式堆要求，如果不满足则交换左右孩子；
  • step4）将H3与没有右子堆的H1进行merge操作，也即最后将case3 转换为了 case2；

结论

现在才知道，左式堆的merge操作其实是一个递归的过程，

递归求解情形：

• 将具有根植较大的堆H2与具有根值较小的堆H1的右子堆合并
• 将新产生的堆作为H1的右子堆
• 交换H1的左右子堆直至合理

看如下解析； （干货——这是最后解析 merge 操作啦）

注意

• 左式堆是建立在具有堆序性的二叉树上；
• 左式堆是建立在零路径长上；
• 左式堆的核心操作是 merge， 无论insert 还是 deleteMin 都是基于 merge操作的；
• 左式堆的merge操作执行后，还要update 左式堆根节点的零路径长， 左式堆根节点的零路径长 == min{儿子的零路径长} +1；
• update 后， 还需要比较 左右零路径长 是否满足左式堆的定义， 如果不满足，还需要交换左式堆根节点的左右孩子；

4 左式堆的插入操作

在知道左式堆合并的基础上，插入操作就很简单了。插入操作可以看成左式堆和只具有一个节点的左式堆的合并操作。那么其最坏时间复杂度也是log(N)。

5 左式堆的删除操作

左式堆的删除操作在理解合并操作的基础上也十分简单，分为如下两个步骤：

• 返回根节点值

• 删除根节点，将左子树和右子树合并，合并后的结果就是删除操作后的新左式堆。

6 左式堆的建堆过程

左式堆的建堆过程就是对输入元素重复插入过程，最坏时间复杂度Nlog(N)，平均时间复杂度O(N)。

7 左式堆的java代码实现。

二叉堆因为是完全二叉树的结构所以采用数组的存储结构，但是左式堆不是完全二叉树需采用链式的结构(需要支持合并操作，也需要采用链式存储结构)。

java代码的如下：

package DataStructureAndAlgorithms.DataStructure.LeftistHeap;

/**
 * 左式堆（递归）
 */
public class LeftistHeap1 {
    public static void main(String[] args) {
        LeftistHeap1 heap = new LeftistHeap1(11);//建立只有一个根节点值为11的左式堆
        for (int i = 1; i < 10; i++) {
            heap.insert(i);
        }
        while (!heap.isEmpty()) {
            System.out.print(heap.deleteMin() + " ");
        }
    }

    //左式堆的节点的定义
    private static class HeapNode {
        private int npl;//零路径长 null path length
        private HeapNode left;//左孩子节点
        private HeapNode right;//右孩子节点
        private int val;//当前节点元素值

        public HeapNode(int val) {
            this.val = val;
            left = null;
            right = null;
            npl = -1;
        }
    }
    private HeapNode root;

    public LeftistHeap1(int val) {
        root = new HeapNode(val);
    }

    //合并两侧左式堆
    private void merge(LeftistHeap1 heap) {
        if (heap != null) {
            root = internalMerge(root, heap.root);//第一次插入时，root 为新建的根节点 11，heap.root = 1
        }
    }

    private HeapNode internalMerge(HeapNode h1, HeapNode h2) {
        if (h1 == null) return h2;
        if (h2 == null) return h1;

        HeapNode result;//当前堆的根节点
        //大根堆的根节点作为新的根节点，小根堆作为新的右孩子
        if (h1.val >= h2.val) {
            h2.right = internalMerge(h2.right, h1);
            result = h2;
        } else {
            h1.right = internalMerge(h1.right, h2);
            result = h1;
        }
        //如果不满足结构性，则调整，另外子节点为空 --> npl = -1,
        int leftNPL = result.left == null ? -1 : result.left.npl;//左孩子的零路径长
        int rightNPL = result.right == null ? -1 : result.right.npl;//右孩子的零路径长
        //左式堆满足左子节点零路径长大于等于右子节点，否则左右交换
        if (leftNPL < rightNPL) {
            HeapNode temp = result.right;
            result.right = result.left;
            result.left = temp;
        }
        //更新npl值，当前节点的子节点到非叶子节点（没有两个子节点的节点）的最短距离 + 1
        result.npl = Math.min(leftNPL, rightNPL) + 1;
        return result;
    }

    /**
     * 插入操作可以看成左式堆和只具有一个节点的左式堆的合并操作
      * @param val
     */
    private void insert(int val) {
        LeftistHeap1 heap = new LeftistHeap1(val);
        merge(heap);
    }

    //对外暴露的删除函数
    private int deleteMin() {
        if (isEmpty())
            return -1; //-1这里代表错误码，堆为空不删除。
        HeapNode node = root;
        root = internalMerge(root.left, root.right);
        return node.val;
    }

    private boolean isEmpty() {
        return root == null;
    }
}