1.概要:
2.LSTM与GRU:

1) LSTM:

2)GRU:

3)概括的来说,LSTM和GRU都能通过各种Gate将重要特征保留,保证其在long-term 传播的时候也不会被丢失;还有一个不太好理解,作用就是有利于BP的时候不容易vanishing:

3.实验结果:
实验用了三个unit,传统的tanh,以及LSTM和GRU:
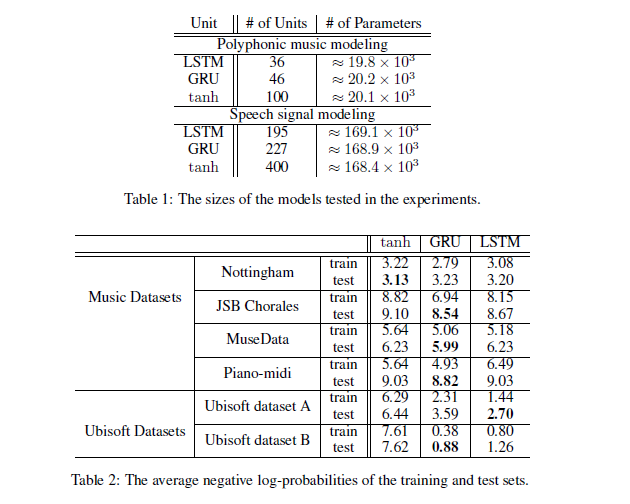
可以发现LSTM和GRU的差别并不大,但是都比tanh要明显好很多,所以在选择LSTM或者GRU的时候还要看具体的task data是什么
不过在收敛时间和需要的epoch上,GRU应该要更胜一筹:

4.代码(keras):
1)LSTM:
class LSTM(Recurrent):
'''
Acts as a spatiotemporal projection,
turning a sequence of vectors into a single vector.
Eats inputs with shape:
(nb_samples, max_sample_length (samples shorter than this are padded with zeros at the end), input_dim)
and returns outputs with shape:
if not return_sequences:
(nb_samples, output_dim)
if return_sequences:
(nb_samples, max_sample_length, output_dim)
For a step-by-step description of the algorithm, see:
http://deeplearning.net/tutorial/lstm.html
References:
Long short-term memory (original 97 paper)
http://deeplearning.cs.cmu.edu/pdfs/Hochreiter97_lstm.pdf
Learning to forget: Continual prediction with LSTM
http://www.mitpressjournals.org/doi/pdf/10.1162/089976600300015015
Supervised sequence labelling with recurrent neural networks
http://www.cs.toronto.edu/~graves/preprint.pdf
'''
def __init__(self, input_dim, output_dim=128,
init='glorot_uniform', inner_init='orthogonal', forget_bias_init='one',
activation='tanh', inner_activation='hard_sigmoid',
weights=None, truncate_gradient=-1, return_sequences=False):
super(LSTM, self).__init__()
self.input_dim = input_dim
self.output_dim = output_dim
self.truncate_gradient = truncate_gradient
self.return_sequences = return_sequences
self.init = initializations.get(init)
self.inner_init = initializations.get(inner_init)
self.forget_bias_init = initializations.get(forget_bias_init)
self.activation = activations.get(activation)
self.inner_activation = activations.get(inner_activation)
self.input = T.tensor3()
self.W_i = self.init((self.input_dim, self.output_dim))
self.U_i = self.inner_init((self.output_dim, self.output_dim))
self.b_i = shared_zeros((self.output_dim))
self.W_f = self.init((self.input_dim, self.output_dim))
self.U_f = self.inner_init((self.output_dim, self.output_dim))
self.b_f = self.forget_bias_init((self.output_dim))
self.W_c = self.init((self.input_dim, self.output_dim))
self.U_c = self.inner_init((self.output_dim, self.output_dim))
self.b_c = shared_zeros((self.output_dim))
self.W_o = self.init((self.input_dim, self.output_dim))
self.U_o = self.inner_init((self.output_dim, self.output_dim))
self.b_o = shared_zeros((self.output_dim))
self.params = [
self.W_i, self.U_i, self.b_i,
self.W_c, self.U_c, self.b_c,
self.W_f, self.U_f, self.b_f,
self.W_o, self.U_o, self.b_o,
]
if weights is not None:
self.set_weights(weights)
def _step(self,
xi_t, xf_t, xo_t, xc_t, mask_tm1,
h_tm1, c_tm1,
u_i, u_f, u_o, u_c):
h_mask_tm1 = mask_tm1 * h_tm1
c_mask_tm1 = mask_tm1 * c_tm1
i_t = self.inner_activation(xi_t + T.dot(h_mask_tm1, u_i))
f_t = self.inner_activation(xf_t + T.dot(h_mask_tm1, u_f))
c_t = f_t * c_mask_tm1 + i_t * self.activation(xc_t + T.dot(h_mask_tm1, u_c))
o_t = self.inner_activation(xo_t + T.dot(h_mask_tm1, u_o))
h_t = o_t * self.activation(c_t)
return h_t, c_t
def get_output(self, train=False):
X = self.get_input(train)
padded_mask = self.get_padded_shuffled_mask(train, X, pad=1)
X = X.dimshuffle((1, 0, 2))
xi = T.dot(X, self.W_i) + self.b_i
xf = T.dot(X, self.W_f) + self.b_f
xc = T.dot(X, self.W_c) + self.b_c
xo = T.dot(X, self.W_o) + self.b_o
[outputs, memories], updates = theano.scan(
self._step,
sequences=[xi, xf, xo, xc, padded_mask],
outputs_info=[
T.unbroadcast(alloc_zeros_matrix(X.shape[1], self.output_dim), 1),
T.unbroadcast(alloc_zeros_matrix(X.shape[1], self.output_dim), 1)
],
non_sequences=[self.U_i, self.U_f, self.U_o, self.U_c],
truncate_gradient=self.truncate_gradient)
if self.return_sequences:
return outputs.dimshuffle((1, 0, 2))
return outputs[-1]
def get_config(self):
return {"name": self.__class__.__name__,
"input_dim": self.input_dim,
"output_dim": self.output_dim,
"init": self.init.__name__,
"inner_init": self.inner_init.__name__,
"forget_bias_init": self.forget_bias_init.__name__,
"activation": self.activation.__name__,
"inner_activation": self.inner_activation.__name__,
"truncate_gradient": self.truncate_gradient,
"return_sequences": self.return_sequences}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
2)GRU:
class GRU(Recurrent):
'''
Gated Recurrent Unit - Cho et al. 2014
Acts as a spatiotemporal projection,
turning a sequence of vectors into a single vector.
Eats inputs with shape:
(nb_samples, max_sample_length (samples shorter than this are padded with zeros at the end), input_dim)
and returns outputs with shape:
if not return_sequences:
(nb_samples, output_dim)
if return_sequences:
(nb_samples, max_sample_length, output_dim)
References:
On the Properties of Neural Machine Translation: Encoder–Decoder Approaches
http://www.aclweb.org/anthology/W14-4012
Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling
http://arxiv.org/pdf/1412.3555v1.pdf
'''
def __init__(self, input_dim, output_dim=128,
init='glorot_uniform', inner_init='orthogonal',
activation='sigmoid', inner_activation='hard_sigmoid',
weights=None, truncate_gradient=-1, return_sequences=False):
super(GRU, self).__init__()
self.input_dim = input_dim
self.output_dim = output_dim
self.truncate_gradient = truncate_gradient
self.return_sequences = return_sequences
self.init = initializations.get(init)
self.inner_init = initializations.get(inner_init)
self.activation = activations.get(activation)
self.inner_activation = activations.get(inner_activation)
self.input = T.tensor3()
self.W_z = self.init((self.input_dim, self.output_dim))
self.U_z = self.inner_init((self.output_dim, self.output_dim))
self.b_z = shared_zeros((self.output_dim))
self.W_r = self.init((self.input_dim, self.output_dim))
self.U_r = self.inner_init((self.output_dim, self.output_dim))
self.b_r = shared_zeros((self.output_dim))
self.W_h = self.init((self.input_dim, self.output_dim))
self.U_h = self.inner_init((self.output_dim, self.output_dim))
self.b_h = shared_zeros((self.output_dim))
self.params = [
self.W_z, self.U_z, self.b_z,
self.W_r, self.U_r, self.b_r,
self.W_h, self.U_h, self.b_h,
]
if weights is not None:
self.set_weights(weights)
def _step(self,
xz_t, xr_t, xh_t, mask_tm1,
h_tm1,
u_z, u_r, u_h):
h_mask_tm1 = mask_tm1 * h_tm1
z = self.inner_activation(xz_t + T.dot(h_mask_tm1, u_z))
r = self.inner_activation(xr_t + T.dot(h_mask_tm1, u_r))
hh_t = self.activation(xh_t + T.dot(r * h_mask_tm1, u_h))
h_t = z * h_mask_tm1 + (1 - z) * hh_t
return h_t
def get_output(self, train=False):
X = self.get_input(train)
padded_mask = self.get_padded_shuffled_mask(train, X, pad=1)
X = X.dimshuffle((1, 0, 2))
x_z = T.dot(X, self.W_z) + self.b_z
x_r = T.dot(X, self.W_r) + self.b_r
x_h = T.dot(X, self.W_h) + self.b_h
outputs, updates = theano.scan(
self._step,
sequences=[x_z, x_r, x_h, padded_mask],
outputs_info=T.unbroadcast(alloc_zeros_matrix(X.shape[1], self.output_dim), 1),
non_sequences=[self.U_z, self.U_r, self.U_h],
truncate_gradient=self.truncate_gradient)
if self.return_sequences:
return outputs.dimshuffle((1, 0, 2))
return outputs[-1]
def get_config(self):
return {"name": self.__class__.__name__,
"input_dim": self.input_dim,
"output_dim": self.output_dim,
"init": self.init.__name__,
"inner_init": self.inner_init.__name__,
"activation": self.activation.__name__,
"inner_activation": self.inner_activation.__name__,
"truncate_gradient": self.truncate_gradient,
"return_sequences": self.return_sequences}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96




























 7145
7145

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








