Diamond iO：实用 iO 的第一缕曙光-CSDN博客

本文链接：https://blog.csdn.net/mutourend/article/details/147775807

1. 引言

当前以太坊基金会PSE的Machina iO团队宣布，其已经成功实现了 Diamond iO: A Straightforward Construction of Indistinguishability Obfuscation from Lattices —— 其在2025年2月提出的、结构简单的不可区分混淆（iO）构造，并完成了其端到端的完整工作流程。详细的开源代码见：

https://github.com/MachinaIO/diamond-io（Rust + Python）

当前的实现在细节上与理论构造略有不同，并仅支持一小部分电路功能。不过，它已经展示了 Diamond iO 所引入的新技术的具体效率，为实现实用化 iO 开辟了新的路径。

2. iO 拥有强大能力，但离实用尚远

在由数据驱动的算法不断加速科技发展的同时，控制这些海量数据的却是中心化实体，个人对自己数据的掌控力正不断减弱。

一个全球性的私密计算平台是实现技术加速与个人数据主权之间平衡、并进一步推动两者发展的唯一可行方案。随着委托给该平台的隐私信息的价值不断上升，必须依赖一个可以在任何安全级别下扩展的安全基础。

与多方计算（Multi-Party Computation, MPC）或多方同态加密（Multi-Party Fully Homomorphic Encryption, MP-FHE）等其他技术不同，MPC和MP-FHE面临隐私可扩展性问题（详情见PSE团队2025年1月博客Why We Can’t Build Perfectly Secure Multi-Party Applications (yet)），iO 完全消除了对可信委员会在分布式设置之后的持续依赖。 换句话说，iO 启用了一种可编程协议，它充当了完美的无需信任的第三方，其安全性仅依赖于密码学难题，就像 Nick Szabo 所定义的 The God Protocols 神之协议。

在一系列关于 iO 的研究之后，Aayush Jain、Huijia Lin 和 Amit Sahai 在 2020 年的突破性工作——Indistinguishability Obfuscation from Well-Founded Assumptions 展示了 iO 可以仅基于标准密码学假设构造，这些假设已经通过十多年研究得到牢固建立。然而，由于构造过程极其复杂，iO 长期以来一直被视为一个理论性的密码学原语。事实上，近期关于 iO 实现的研究——2015年论文Idea: Benchmarking Indistinguishability Obfuscation – A Candidate Implementation 报告称，对一个 2 位乘法电路进行混淆的模拟结果是：大约需要 $10^{27}$ 年的时间以及 20 ZB（泽字节）的内存。

3. Diamond iO：一个可实现的 iO 构造

Diamond iO 通过提出一个基于格的全新 iO 构造，成功克服了以往难以实现的障碍。这一构造足够简单，可以实际落地。此前 iO 方案中一个常见的瓶颈是严重依赖功能加密（functional encryption，FE）中开销高昂（且递归）的运算。Diamond iO 通过改用简单的矩阵运算解决了这一问题。

https://github.com/MachinaIO/diamond-io)实现了Diamond iO: A Straightforward Construction of Indistinguishability Obfuscation from Lattices 论文中第 4 节定义的构造。此次实现与理论构造之间有以下一些小差异：

RLWE 与 LWE。 论文在误差学习（learning with error，LWE）设定下描述该方案，而代码实现则采用了环误差学习（RLWE）设定。在实践中，用多项式环替代了有限域元素，使得每个矩阵中能打包更多信息位，并可利用数论变换高效地完成乘法运算。
伪随机函数（PRF）方案。 理论构造中通过 FHE 同态计算 PRF；而在代码实现中，不使用 FHE，而是根据评估者的输入位复用密钥，作为 PRF 密钥来执行。这一机制将在即将发布的论文更新版本中详细说明。
电路模型。 理论构造混淆整个电路，而代码实现中，混淆器设置一个私钥 $k$ 和一个电路 $C$ ，以获得一个只隐藏 $k$ 的混淆程序，电路 $C$ 则保持公开。评估者随后可以在不交互的情况下，对其输入 $x$ 执行混淆程序，得到 $C (k, x)$ ，而无法获取其他信息。这与实际应用场景（详情见2025年4月博客Why program obfuscation matters）一致，即通常只需隐藏签名或解密密钥，而functionality功能需保持透明。
FHE 方案。 理论构造采用了 GSW FHE（详情见2013年论文Homomorphic Encryption from Learning with Errors: Conceptually-Simpler, Asymptotically-Faster, Attribute-Based），而实现则采用了基于 RLWE 的更简单加密方法，出自 LPR10——2010年论文On Ideal Lattices and Learning with Errors Over Rings。该方案仅支持对加密的二进制向量进行线性同态操作。相比 GSW，它所需的密文位数更少。
缺少伪随机预言机。 伪随机预言机——见2023年论文The Pseudorandom Oracle Model
and Ideal Obfuscation（可通过哈希函数实现）在安全性证明中是必要的，确保 iO 能支持不仅仅是伪随机功能，还包括通用功能（详见 BDJ+24——见2024年论文Pseudorandom Obfuscation and Applications 第 5.4 小节）。不过目前该部分尚未在实现中加入，因为所需的哈希函数仍过于复杂。

尽管以上差异（除第一项外）均是为了降低 AKY24——2024年论文Compact Pseudorandom Functional Encryption from Evasive LWE 中功能加密方案的实现复杂度，但 Diamond iO 的关键创新点——即将评估者输入位插入由混淆器提供的 FE 密文的矩阵处理过程——仍按理论构造实现（仅作了些微优化）。因此，尽管存在部分差异，该实现依然成功展示了Diamond iO论文中所提出新技术的具体效率。

4. 超越理论：基准测试结果

在基准测试场景中，混淆器设置了一个公开电路 $C$ ，其算术深度（加法和乘法层数）和输入规模均可变。作为混淆算法的一部分，混淆器会对一个二进制向量形式的硬编码密钥 $k$ 进行采样，并将其嵌入到被混淆的电路中。随后，混淆后的电路被发布，任何评估者都可以在其动态选择的输入 $x$ 上运行该电路，获得 $C (k, x)$ ，无需与混淆器交互，也无法获取 $k$ 的信息（除非能从 $C (k, x)$ 中推断出来）。

// 公共电路 C
let mut public_circuit = PolyCircuit::new();

// 输入：BaseDecompose(ct)、评估者输入
// 输出：BaseDecompose(ct) * acc
{
    let inputs = public_circuit.input((2 * log_base_q) + 1);
    let mut outputs = vec![];
    let eval_input = inputs[2 * log_base_q];

    // 根据 add_n 和 mul_n 的值计算 acc
    let mut acc = if add_n == 0 {
        public_circuit.const_one_gate()
    } else {
        public_circuit.const_zero_gate()
    };
    for _ in 0..add_n {
        acc = public_circuit.add_gate(acc, eval_input);
    }
    for _ in 0..mul_n {
        acc = public_circuit.mul_gate(acc, eval_input);
    }

    // 计算输出
    for ct_input in &inputs[0..2 * log_base_q] {
        let muled = public_circuit.mul_gate(*ct_input, acc);
        outputs.push(muled);
    }
    public_circuit.output(outputs);
}

在下面的描述中，“乘法深度”指的是公共电路中的乘法门深度，而不是整个电路的深度。即使该深度为 0，整个被混淆和被评估的电路也至少有一个深度，因为最终的 FHE 解密步骤包含一次内积操作。

通过将公共电路设置为恒等函数并验证评估输出是否与混淆器采样的硬编码密钥相匹配，确认了实现的正确性。

需要特别强调的一个性能要点是：

混淆操作是每个应用仅需进行一次的过程。

由于可以假设混淆器拥有强大的硬件资源，因此优化的重点应放在评估阶段，它是一个重复执行、性能关键的过程。

4.1 基准测试设置

使用未启用任何功能标志（feature flags）编译的 dio CLI 可执行文件，在上述场景下对实现进行了基准测试。对于每个实验配置，分别测量了执行时间、内存消耗以及混淆电路的大小，并取其平均值。基准测试所用公共电路中的加法层和乘法层（即深度）根据实验设置进行了调整。

选用了根据 https://github.com/malb/lattice-estimator 评估能够提供至少 80 位安全性（对抗当前已知最佳攻击方式）的最优参数。这一过程通过所实现的模拟器脚本自动完成。

4.2 基准测试 1：电路复杂度（固定输入规模）

在第一个基准测试中，将输入规模固定为 1 位，通过改变公共电路中乘法的深度来扩展电路复杂度，如下表所示（表 1）。此处，忽略 FHE 解密过程中用于内积计算的一个乘法深度，因为这是与公共电路定义无关的通用操作。
表1——基准测试 1的试验设置：

乘法深度（Multiplicative depth）	参数配置	最终电路门数（输入 / 常量 / 加法 / 减法 / 乘法）
0	ID 33	46 / 108 / 36 / 0 / 180
5	ID 34	58 / 144 / 68 / 4 / 260
10	ID 35	76 / 198 / 106 / 4 / 370

这些实验在以下环境中进行：

机器配置： AWS i4i.8xlarge 实例（32 核 vCPU，256 GB 内存）
基准测试所用代码提交版本： f3b2fdc

基准测试 1 的结果： 表 2 总结了每个乘法深度下电路混淆执行时间、峰值内存使用以及混淆电路大小的结果。第二列、第三列和第四列分别表示混淆电路并写入磁盘所需时间、从磁盘加载混淆电路到内存所需时间，以及评估该电路所需时间。

表2——每个乘法深度下的基准测试1的结果：

乘法深度	混淆时间（分钟）	加载时间（分钟）	执行时间（分钟）	峰值内存使用（GB）	混淆电路大小（GB）
0	15.80	4.575	2.542	34.30	6.303
5	39.85	12.84	7.789	80.38	10.79
10	129.3	42.16	29.94	225.1	19.77

图1——不同乘法深度下的各阶段执行时间变化图：
在这里插入图片描述
图2——不同乘法深度下的峰值内存使用与混淆电路大小变化图：

图 1 展示了各个操作的执行时间随乘法深度增加而呈超线性增长的趋势。图 2 所示的峰值内存使用量和混淆电路大小也遵循相同趋势。

这一趋势可从理论上解释如下：

在评估阶段，累积误差的上界会随电路深度呈指数级增长。
- 为了保持正确性，模数 $q$ 的位长必须与电路深度成正比地增长。
- 在混淆电路中包含的矩阵中，最大的矩阵（即preimage原像矩阵）的大小大致随 $q$ 的位长或其平方而增长。
- 因此，其位长至少以深度的平方速度增加，导致总体执行时间的增长快于线性趋势。

4.3 基准测试 2：输入规模（固定电路复杂度）

在第二组基准测试中，将公共电路的复杂度保持与基准测试 1 中乘法深度为 0 的情形一致，并变更输入位数，如表 3 所示。

表3——基准测试 2 的实验设置：

输入规模（比特）	参数配置	最终电路门数量（输入 / 常量 / 加法 / 减法 / 乘法）
1	ID 33	46 / 108 / 36 / 0 / 180
2	ID 36	58 / 144 / 48 / 0 / 240
4	ID 39	82 / 216 / 72 / 0 / 360

这些实验在如下环境中进行：

机器配置： AWS i4i.16xlarge 实例（64 个 vCPU，512 GB 内存）
基准测试使用的代码提交版本： a2fe732

与基准测试 1 中的实现不同，基准测试 2 的实现仅在每次评估步骤中从磁盘加载所需的部分混淆电路，从而避免了即使在输入规模较大时也可能发生的内存溢出。

基准测试 2 的结果。 表 4 总结了不同输入规模下的混淆时间、评估时间、峰值内存使用和混淆电路大小。其中第三列包括在评估过程中从磁盘加载混淆电路所需的时间。

表4——不同输入规模下的基准测试2的结果：

输入规模（比特）	混淆时间（分钟）	评估时间（分钟）	峰值内存使用（GB）	混淆电路大小（GB）
1	12.55	2.925	20.80	6.303
2	52.01	11.54	62.97	20.76
4	372.8	85.19	270.5	88.05

图 3——输入规模递增下的执行时间变化图：
在这里插入图片描述

图 4——输入规模递增下的峰值内存使用和混淆电路大小变化图：
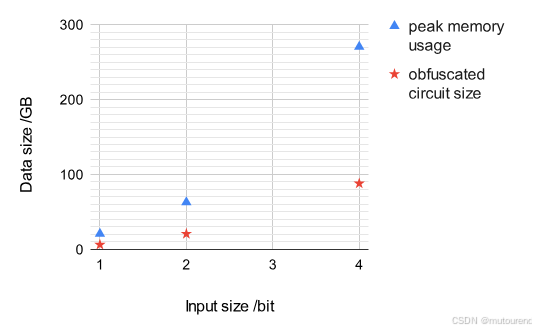
在这里插入图片描述

图 3 和图 4 展示了与基准测试 1 相比，基准测试 2 中的各项指标随着输入规模增长而上升得更快。理论分析表明，与乘法深度类似，模数 $q$ 的位长度也会随着输入规模线性增长。然而，这种增长不仅会导致每个矩阵变大，还会线性增加需要使用的原像矩阵数量。因此，理论上可以解释为何执行时间和数据大小的增长速度超过了基准测试 1 中观察到的水平。

5. 讨论：迈向实用可行性

这些基准测试结果表明，无论是混淆时间、评估时间，还是混淆电路的大小，在乘法深度和输入规模的变化下，增长趋势都是非线性的。然而值得鼓舞的是，评估时间的增长速度慢于其他两者，这是一个积极信号，因为评估是最频繁执行的过程。

尽管当前实现距离实际可用的电路规模似乎还有一定距离，但根据 GGH+13——2013年论文Candidate Indistinguishability Obfuscation and Functional Encryption for all circuits 和 BIS+17——2017年论文Lattice-Based SNARGs and Their Application to More Efficient Obfuscation 的观点，实际上并不需要支持对任意复杂电路的混淆。相反，只需要支持包含以下逻辑的电路即可：

通过零知识证明（ZKP）验证 FHE 评估的正确性，并根据结果有条件地使用嵌入的密钥解密给定密文。
这样一来，可以将应用逻辑外包给一个 FHE 程序，同时专注于高效地混淆一个具有固定乘法深度和输入规模的电路。

6. 未来研究方向

下一步将着手解决以下安全性与效率方面的挑战。

安全性挑战有：
- 关于 evasive LWE 假设的近期攻击。 以下四篇论文均发表于 Diamond iO 论文之后，它们提出了针对 evasive LWE 假设的新型攻击。尽管 Diamond iO 的安全性证明高度依赖这一假设，但据Machina iO团队所知，这些攻击目前仅在特定参数和采样器设定下有效，而这些设定并不一定适用于现实中基于该假设的密码方案。Machina iO团队目前正在评估这些攻击是否可以适用于Diamond iO构造中使用的具体参数和采样方式。
- 2025年论文 Simple and General Counterexamples for Private-Coin Evasive LWE（针对私密币 evasive LWE 的简单且通用的反例）
- 2025年论文 Evasive LWE: Attacks, Variants & Obfustopia（evasivse LWE：攻击、变体与混淆乌托邦）
- 2025年论文 Lattice-Based Post-Quantum iO from Circular Security with Random Opening Assumption（基于格的后量子 iO 构造：来自循环安全与随机揭示假设）
- 2025年论文 A Note on Obfuscation-based Attacks on Private-Coin Evasive LWE（关于基于混淆的对私密币 evasive LWE 的攻击研究）
- 分布式混淆。 细心的读者可能已经注意到，如果混淆器仍然掌握混淆程序中的秘密，那么 iO 几乎毫无意义。一个朴素的解决方案是将混淆过程置于 MPC（多方安全计算）中执行，但这在现实中极其不切实际。很期待探索更加可行的方式来实现混淆的分布式可信初始化，因为这个议题在现有文献中基本未被重视。
效率方面的挑战有：
- 评估过程中的噪声刷新。 如前所述，只需支持对一个验证零知识证明并随后解密给定 FHE 密文的电路进行混淆。然而，由于当前实现支持的输入规模有限，还无法对这样一个电路进行混淆。具体来说，由于输入规模越大，累计误差呈指数增长，导致模数位数线性增长，因此Machina iO团队正在研究在评估过程中降低误差的技术，如 HLL23——2023年论文Attribute-Based Encryption for Circuits of Unbounded Depth from Lattices: Garbled Circuits of Optimal Size, Laconic Function Evaluation, and More 中提出的用于 BGG+ 编码的技术。

7. Machina iO团队介绍

Machina（读音为“mah-kin-ah”）iO 是 Privacy and Scaling Explorations（PSE）项目中的一部分，致力于将不可区分混淆（iO）从理论推进到实践。将持续在研究与工程方面努力，并计划发布一系列文章，解释技术背后的核心理念、愿景，以及在实现过程中汲取的经验教训。

8. Machina iO团队致谢

衷心感谢 OpenFHE 和 openfhe-rs 的开发者们。这些开源格加密与 FHE 库中对 trapdoor 采样、RLWE 原语以及 Rust 绑定的优化实现，为构建 Diamond iO 提供了关键支持。同时也感谢 Yuriy Polyakov 教授在 preimage 采样方面提供的宝贵建议，以及对 Diamond iO 优化实现的深刻反馈。