[完]机器学习实战 第十四章 利用SVD简化数据

本章内容：

• SVD矩阵分解
• 推荐引擎
• 利用SVD提升推荐引擎的性能

餐馆可分为很多类别，不同的专家对其分类可能有不同依据。实际中，我们可以忘掉专家，从数据着手，可对记录用户关于餐馆观点的数据进行处理，并从中提取出其背后的因素。这些因素可能会与餐馆的类别、烹饪时采用的某个特定配料，或其他任意对象一致。然后，可利用这些因素来估计人们对没有去过的餐馆的看法。

提取这些信息的方法称为奇异值分解（Singular Value Decomposition，SVD）。从生物信息学到金融学等在内的很多应用中，SVD都是提取信息的强大工具。

本章会介绍SVD的概念及其能进行数据约简的原因，然后，介绍基于Python的SVD实现以及将数据映射到低维空间的过程。还将学习推荐引擎的概念和它们实际运行过程。为提高SVD的精度，我们将会把其应用到推荐系统中，该推荐系统将会帮助人们寻找到合适的餐馆，最后，会讲述一个SVD在图像压缩中的例子。

一、SVD的应用

奇异值分解的优缺点：

• 优点：简化数据，去除噪声，提高算法的结果。
• 缺点：数据的转换可能难以理解。
• 使用数据类型：数值型数据。

利用SVD，可使用小得多的数据集来表示原始数据集，这样会去除噪声数据和冗余信息。在此，我们主要是为了从数据中抽取信息。基于此，可把SVD看成是从有噪声数据中抽取相关特征。

1-1 隐形语义索引

最早的SVD应用之一是信息检索。将利用SVD的方法称为隐性语义索引（Latent Semantic Indexing，LSI）或隐性语义分析（Latent Semantic Analysis，LSA）。

在LSI中，一个矩阵是由文档和词语组成的。当我们在该矩阵上应用SVD时，就会构建出多个奇异值。这些奇异值代表了文档中的概念或主题，这一特点可以用于更高效的文档搜索。在词语拼写错误时，只基于词语存在与否的简单搜索方法会遇到问题。简单搜索的另一个问题就是同义词的使用。即，当查找一个词时，其同义词所在的文档可能并不会匹配上。如果从上千篇相似的文档中抽取出概念，那么同义词就会映射为统一概念。

1-2 推荐系统

SVD的另一个应用是推荐系统。简单版本的推荐系统能计算项或人之间的相似度。更先进的方法则先利用SVD从数据中构建一个主题空间，然后再在该空间下计算其相似度。图1给出的矩阵，由餐馆的菜和品菜师对这些菜的意见构成。品菜师可采用1-5之间的任意整数来对菜评级。若没品尝过某道菜，则评0级。

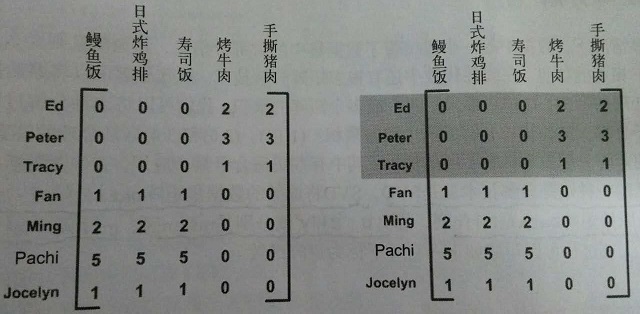
图1　餐馆的菜及其评级的数据。对此矩阵进行SVD处理则可以将数据压缩到若干概念中。在右边的矩阵当中，标出了一个概念。

对上述矩阵进行SVD处理，会得到两个奇异值。因此，就会仿佛有两个概念或主题与此数据集相关联。看看能否通过观察图中的0来找到这个矩阵的具体概念。观察有图的阴影部分，看起来Ed、Peter和Tracy对“烤牛肉”和“手撕猪肉”进行了评级，同时这三人未对其他菜评级。烤牛肉和手撕猪肉都是美式烧烤餐馆才有的菜，其他菜则在日式餐馆才有。

可以将奇异值想象成一个新空间。与图1中的矩阵给出的五维或者七维不同，我们最终的矩阵只有二维。这二维分别是什么呢？能告诉我们数据的什么信息？这二维分别对应图中给出的两个组，右图中已经标示出了其中的一个组。可基于每个组的共同特征来命名这二维，比如得到的美式BBQ和日式食品这二维。

如何将原始数据变换到上述新空间中呢？下一节会进一步详细地介绍SVD，将会了解到SVD是如何得到$U$和$V^T$两个矩阵。$V^T$矩阵会将用户映射到BBQ/日式食品空间去。类似地，$U$矩阵会将餐馆的菜映射到BBQ/日式食品空间去。真实的数据通常不会像图1中的矩阵那样稠密或整齐，这里如此只是为了便于说明问题。

推荐引擎中可能会有噪声数据，比如，某人对某些菜的评级就可能存在噪声，并且推荐系统也可将数据抽取为这些基本主题。基于这些主题，推荐系统就能取得比原始数据更好的推荐效果。

二、矩阵分解

在很多情况下，数据中的一小段携带了数据集中的大部分信息，而其他信息要么是噪声，要么就是毫不相关的信息。矩阵分解可将原始矩阵表示成新的易于处理的形式，新形式是两个或多个矩阵的乘积。

不同的矩阵分解技术具有不同的性质，其中有些更适合于某个应用，有些则更适合于其他应用。最常见的一种矩阵分解技术就是SVD。SVD将原始的数据集矩阵Data分解成三个矩阵$U$、$\Sigma$、$V^T$。如果原始矩阵Data是m行n列，则有如下等式：

$$Data_{m\times n}=U_{m\times m} \Sigma_{m\times n} V^T_{n\times n}$$

上述分解中会构建出一个矩阵$\Sigma$，该矩阵只有对角元素，其他元素均为0。另一个惯例就是，$\Sigma$的对角元素是从大到小排列的。这些对角元素称为奇异值（Singular Value），它们对应了原始数据集矩阵Data的奇异值。回想PCA章节，得到的是矩阵的特征值，它们告诉我们数据集中的重要特征。$\Sigma$中的奇异值也是如此。奇异值和特征值时有关系的。这里的奇异值就是矩阵$Data*Data^T$特征值的平方根。

矩阵$\Sigma$只有从大到小排列的对角元素。在科学和工程中，一致存在这样一个普遍事实：在某个奇异值的数目（r个）之后，其他的奇异值都置为0。这就意味着数据集中仅有r个重要特征，而其余特征则都是噪声或冗余特征。

三、利用Python实现SVD

NumPy由一个称为linalg的线性代数工具箱，利用此工具箱可实现如下矩阵的SVD处理：

[17