1.1 整数字符串转化
例题1 整数转化为字符串
#include <stdlib.h>
int main() {
int num = 65535;
char str[7] = {0};
char temp[7] = {0};
int i = 0, j = 0;
while(num) {
temp[i] = num%10 + '0';
i++;
num = num/10;
}
temp[i] = '\0';
printf("temp: %s\n", temp);
i = i - 1;
//逆转
while(i >= 0) {
str[j] = temp[i];
i--;
j++;
}
str[j] = '\0';
printf("str: %s\n", str);
char*itoa(intvalue,char*string,intradix);
//itoa(num, str, 10);
//printf("integer = %d, str = %s\n", num, str);
return 0;
}
int main() {
int num = 65535;
char str[7] = {0};
char temp[7] = {0};
int i = 0, j = 0;
while(num) {
temp[i] = num%10 + '0';
i++;
num = num/10;
}
temp[i] = '\0';
printf("temp: %s\n", temp);
i = i - 1;
//逆转
while(i >= 0) {
str[j] = temp[i];
i--;
j++;
}
str[j] = '\0';
printf("str: %s\n", str);
char*itoa(intvalue,char*string,intradix);
//itoa(num, str, 10);
//printf("integer = %d, str = %s\n", num, str);
return 0;
}
运行如图所示:且图中的注释代码也可以完成类似的功能。
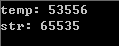
例题2 字符串转化为整数
int main() {
int i = 0, sum = 0;
char temp[7] = {'1','2','3','4','5','\0'};
while(temp[i]) {
sum = sum*10 + (temp[i] - '0');
i++;
}
int atoi(const char *nptr);
//sum = atoi(temp);
printf("sum: %d\n", sum);
return 0;
}
int i = 0, sum = 0;
char temp[7] = {'1','2','3','4','5','\0'};
while(temp[i]) {
sum = sum*10 + (temp[i] - '0');
i++;
}
int atoi(const char *nptr);
//sum = atoi(temp);
printf("sum: %d\n", sum);
return 0;
}
运行结果如图所示:
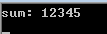
1.2 字符数组和strcpy
例题1 strcpy实现
char* strcpy1(char *strDest, const char *strSrc) {
if ((strSrc == NULL) || (strDest == NULL)) {
return NULL;
}
char* address = strDest;
while(*strSrc != '\0') {
*strDest = *strSrc;
strDest++;
strSrc++;
}
return address;
}
int main() {
const char srcstr[] = {"adgdkgdkfal"};
char strdst[256] = {0};
int length = 0;
strcpy1(strdst, srcstr);
printf("strdst: %s\n", strdst);
length = strlen(strcpy1(strdst, srcstr));
printf("length of strdst: %d", length);
return 0;
}
if ((strSrc == NULL) || (strDest == NULL)) {
return NULL;
}
char* address = strDest;
while(*strSrc != '\0') {
*strDest = *strSrc;
strDest++;
strSrc++;
}
return address;
}
int main() {
const char srcstr[] = {"adgdkgdkfal"};
char strdst[256] = {0};
int length = 0;
strcpy1(strdst, srcstr);
printf("strdst: %s\n", strdst);
length = strlen(strcpy1(strdst, srcstr));
printf("length of strdst: %d", length);
return 0;
}
运行结果如图所示:
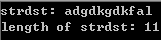
例题2 循环右移
#include <string.h>
#define MAX_LEN 256
void LoopMove(char *pStr, int steps) {
int len = strlen(pStr);
char tmp[MAX_LEN] = {0};
//char* strcpy(char *strDest, const char *strSrc)
strcpy(&tmp[0], pStr+(len-steps));
strcpy(&tmp[steps], pStr);
//strcpy() which uses '\0' to indicate the end. otherwise is string constant.
//must be line.
tmp[len] = '\0';
strcpy(pStr, tmp);
}
void LoopMove1(char *pStr, int steps) {
int len = strlen(pStr);
char tmp[MAX_LEN] = {0};
//void *memcpy(void *dest, const void *src, size_t n)
memcpy(&tmp[0], pStr+(len-steps), steps);
memcpy(&tmp[steps], pStr, len-steps);
memcpy(pStr, tmp, len);
}
int main() {
char data[] = {"abdweifalg"};
printf("before loopmove: %s\n", data);
//LoopMove(data, 3);
LoopMove1(data, 3);
printf("after loopmove: %s\n", data);
return 0;
}
#define MAX_LEN 256
void LoopMove(char *pStr, int steps) {
int len = strlen(pStr);
char tmp[MAX_LEN] = {0};
//char* strcpy(char *strDest, const char *strSrc)
strcpy(&tmp[0], pStr+(len-steps));
strcpy(&tmp[steps], pStr);
//strcpy() which uses '\0' to indicate the end. otherwise is string constant.
//must be line.
tmp[len] = '\0';
strcpy(pStr, tmp);
}
void LoopMove1(char *pStr, int steps) {
int len = strlen(pStr);
char tmp[MAX_LEN] = {0};
//void *memcpy(void *dest, const void *src, size_t n)
memcpy(&tmp[0], pStr+(len-steps), steps);
memcpy(&tmp[steps], pStr, len-steps);
memcpy(pStr, tmp, len);
}
int main() {
char data[] = {"abdweifalg"};
printf("before loopmove: %s\n", data);
//LoopMove(data, 3);
LoopMove1(data, 3);
printf("after loopmove: %s\n", data);
return 0;
}
运行结果如下图所示:
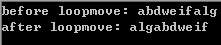
1.3 数组初始化与数组越界
例题1
#include <string.h>
void test1() {
char string[11];
char *str1 = "0123456789";
strcpy(string, str1);
printf("test1: %s\n", string);
}
void test2() {
char string[10], str1[10];
for(int i = 0; i < 9; i++) {
str1[i] = 'a';
}
str1[9] = '\0';
strcpy(string, str1);
printf("test2: %s\n", string);
}
void test3(char *str1) {
char string[10];
if (strlen(str1) < 10) {
strcpy(string, str1);
}
printf("test3: %s\n", string);
}
int main() {
char *str = "012345678";
test1();
test2();
test3(str);
return 0;
}
void test1() {
char string[11];
char *str1 = "0123456789";
strcpy(string, str1);
printf("test1: %s\n", string);
}
void test2() {
char string[10], str1[10];
for(int i = 0; i < 9; i++) {
str1[i] = 'a';
}
str1[9] = '\0';
strcpy(string, str1);
printf("test2: %s\n", string);
}
void test3(char *str1) {
char string[10];
if (strlen(str1) < 10) {
strcpy(string, str1);
}
printf("test3: %s\n", string);
}
int main() {
char *str = "012345678";
test1();
test2();
test3(str);
return 0;
}
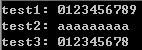
运行结果如下图所示:
例题2
#define MAX 255
int main() {
char p[MAX+1];
unsigned char ch;
for(ch = 0; ch < MAX; ch++) {
p[ch] = ch;
printf("ch: %d\n", ch);
}
p[ch] = ch;
printf("ch: %d\n", ch);
return 0;
}
int main() {
char p[MAX+1];
unsigned char ch;
for(ch = 0; ch < MAX; ch++) {
p[ch] = ch;
printf("ch: %d\n", ch);
}
p[ch] = ch;
printf("ch: %d\n", ch);
return 0;
}
1.4 字符串其他问题
例题1 strstr()函数实现:该函数返回值是主串中字符子串的位置以后的所有字符。
const char* strstr1(const char* string, const char* subStrSet) {
int i = 0, j = 0;
for(i = 0; string[i] != '\0'; i++) {
if (string[i] == subStrSet[j]) {
while(string[i++] == subStrSet[j++]) {
if (subStrSet[j] == '\0') {
return &string[i-j];
}
}
}
}
return NULL;
}
int main() {
char *string = "123456789";
char *substr = "46";
char *substr1 = "456";
char subStrR[10];
const char *p = subStrR;
p = strstr1(string, substr1);
printf("after strstr: %s", p);
return 0;
}
int i = 0, j = 0;
for(i = 0; string[i] != '\0'; i++) {
if (string[i] == subStrSet[j]) {
while(string[i++] == subStrSet[j++]) {
if (subStrSet[j] == '\0') {
return &string[i-j];
}
}
}
}
return NULL;
}
int main() {
char *string = "123456789";
char *substr = "46";
char *substr1 = "456";
char subStrR[10];
const char *p = subStrR;
p = strstr1(string, substr1);
printf("after strstr: %s", p);
return 0;
}
运行结果如图所示:

例题2 句子翻转,如"i come from tianjin." 转换为“tianjin. from com i”
#include <string.h>
int main() {
char charStr[] = {"i come from tianjin."};
int j = strlen(charStr) - 1;
char temp = 0;
int i = 0;
int begin = 0, end = 0;
while(j > i) {
temp = charStr[j];
charStr[j] = charStr[i];
charStr[i] = temp;
j--;
i++;
}
printf("charStr: %s\n", charStr);
i = 0;
while(charStr[i] != '\0') {
if (charStr[i] != ' ') {
begin = i;
while(charStr[i] && charStr[i] != ' ') {
i++;
}
i = i -1;
end = i;
}
while(end > begin) {
temp = charStr[begin];
charStr[begin] = charStr[end];
charStr[end] = temp;
begin++;
end--;
}
i++;
}
printf("charStr: %s", charStr);
return 0;
}
int main() {
char charStr[] = {"i come from tianjin."};
int j = strlen(charStr) - 1;
char temp = 0;
int i = 0;
int begin = 0, end = 0;
while(j > i) {
temp = charStr[j];
charStr[j] = charStr[i];
charStr[i] = temp;
j--;
i++;
}
printf("charStr: %s\n", charStr);
i = 0;
while(charStr[i] != '\0') {
if (charStr[i] != ' ') {
begin = i;
while(charStr[i] && charStr[i] != ' ') {
i++;
}
i = i -1;
end = i;
}
while(end > begin) {
temp = charStr[begin];
charStr[begin] = charStr[end];
charStr[end] = temp;
begin++;
end--;
}
i++;
}
printf("charStr: %s", charStr);
return 0;
}
运行结果如图所示:先全部翻转,再每个单词翻转。

1.5 字符子串问题
例题1 转换字符格式为原来字符串里的字符+该字符连续出现的个数
#include <string.h>
int main() {
char inchar[] = {"12344668899999"};
char outchar[50];
int len = strlen(inchar);
int k = 0, count = 1, j = 0;
for(k = 0; k < len; k++) {
if(inchar[k+1] == inchar[k]) {
count++;
} else {
// int sprintf( char *buffer, const char *format, [ argument] … )
sprintf(&outchar[j], "%c%d", inchar[k], count);
j = j + 2;
count = 1;
}
}
printf("outchar: %s", outchar);
return 0;
}
int main() {
char inchar[] = {"12344668899999"};
char outchar[50];
int len = strlen(inchar);
int k = 0, count = 1, j = 0;
for(k = 0; k < len; k++) {
if(inchar[k+1] == inchar[k]) {
count++;
} else {
// int sprintf( char *buffer, const char *format, [ argument] … )
sprintf(&outchar[j], "%c%d", inchar[k], count);
j = j + 2;
count = 1;
}
}
printf("outchar: %s", outchar);
return 0;
}
运行结果如图所示:























 825
825

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








