二叉查找树(Binary Search Tree)
一、二叉查找树的定义
----或是一棵空树;或者是具有如下性质的非空二叉树:
(1)左子树的所有结点均小于根的值;
(2)右子树的所有结点均大于根的值;
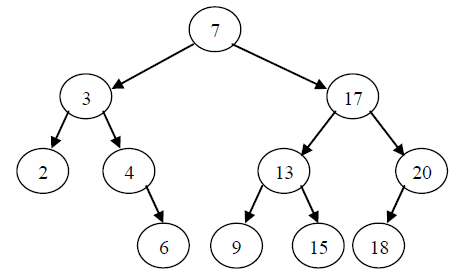
结论:中序遍历一棵二叉查找树可以得到一个按关键字递增的有序序列。
1、查找
查找的递归实现 :
private Node binTSearchRe(BinTreeNode rt, Object ele) {
if (rt == null)
return null;
switch (strategy.compare(ele, rt.getData())) {
case 0:
return rt; // 等于
case -1:
return binTSearchRe(rt.getLChild(), ele);// 小于
default:
return binTSearchRe(rt.getRChild(), ele);// 大于
}
}调用
// 返回查找表中与元素ele关键字相同的元素位置;否则,返回null
public Node search(Object ele) {
return binTSearch(root, ele);
}查找的非递归实现
private Node binTSearch(BinTreeNode rt, Object ele) {
while (rt != null) {
switch (strategy.compare(ele, rt.getData())) {
case 0:
return rt; // 等于
case -1:
rt = rt.getLChild();
continue;// 小于
default:
rt = rt.getRChild(); // 大于
}
}
return null;
}
查找分析
含有n个结点的二叉查找树的平均查找长度和树的形态有关。
在具有n个结点的二叉树中,树的最小高度为log n ,即在最好的情况下二叉查找树的平均查找长度与折半查找一样与log n 成正比。具有n个结点的二叉树可以退化为一个单链表,其深度为n-1,此时其平均查找长度为(n+1)/2,与顺序查找相同,这是最差的情况。在平均情况下,如果随机生成二叉查找树,其平均查找长度和log n 是等数量级的。
2、最大最小值
在二叉查找树中,最小元素总是能够通过根结点向左不断深入,直到到达最左的一个叶子结点找到;而最大元素总是能够通过根结点向右不断深入,直到到达最右的一个叶子结点找到。
Max
public Node max(BinTreeNode v) {
if (v != null)
while (v.hasRChild())
v = v.getRChild();
return v;
}3、前驱和后续
在二叉查找树中确定某个结点v 的后续结点的算法思想如下:如果结点v 有右子树,那么v 的后续结点是v 的右子树中关键字最小的;如果结点v 右子树为空,并且v 的后续结点存在,那么v 的后续结点是从v(包含v)到根的路径上第一个作为左孩子结点的父结点。
代码:求v在中序遍历序列中的后续结点
// 返回结点v在中序遍历序列中的后续结点
private BinTreeNode getSuccessor(BinTreeNode v) {
if (v == null)
return null;
if (v.hasRChild())
return (BinTreeNode) min(v.getRChild());
while (v.isRChild())
v = v.getParent();
return v.getParent();
}代码:求v在中序遍历序列中的前驱结点
// 返回结点v在中序遍历序列中的前驱结点
private BinTreeNode getPredecessor(BinTreeNode v) {
if (v == null)
return null;
if (v.hasLChild())
return (BinTreeNode) max(v.getLChild());
while (v.isLChild())
v = v.getParent();
return v.getParent();
}4、插入
为了判定新结点的插入位置,需要从根结点开始逐层深入,判断新结点关键字与各子树根结点关键字的大小,若新结点关键字小,则向相应根结点的左子树深入,否则向右子树深入;直到向某个结点的左子树深入而其左子树为空,或向某个结点的右子树深入而其右子树为空时,则确定了新结点的插入位置。
// 按关键字插入元素ele
public void insert(Object ele) {
BinTreeNode p = null;
BinTreeNode current = root;
while (current != null) { // 找到待插入位置
p = current;
if (strategy.compare(ele, current.getData()) < 0)
current = current.getLChild();
else
current = current.getRChild();
}
if (p == null)
root = new BinTreeNode(ele); // 树为空
else if (strategy.compare(ele, p.getData()) < 0)
p.setLChild(new BinTreeNode(ele));
else
p.setRChild(new BinTreeNode(ele));
}5、删除算法
对于二叉查找树,删除树上一个结点相当于删除有序序列中的一个记录,删除后仍需保持二叉查找树的特性。在二叉查找树中删除的结点不总是叶子结点,因此在删除一个非叶子结点时需要处理该结点的子树。
如何删除一个结点?
下面我们分三种情况讨论结点v 的删除:
⑴如果结点v为叶子结点,即其左右子树Pl和Pr均为空,此时可以直接删除该叶子结点v,而不会破坏二叉查找树的特性,因此直接从树中摘除v即可。
⑵如果结点v只有左子树Pl或只有右子树Pr,此时,当结点v是左孩子时,只要令Pl或Pr为其双亲结点的左子树即可;当结点v是右孩子时,只要令Pl或Pr为其双亲结点的右子树即可。
⑶如果结点v既有左子树Pl又有右子树Pr,此时,不可能进行如上简单处理。为了在删除结点v之后,仍然保持二叉查找树的特性,我们必须保证删除v之后,树的中序序列必须仍然有序。为此,我们可以先用中序序列中结点v的前驱或后序替换v,然后删除其前驱或后序结点即可,此时v的前驱或后序结点必然是没有右孩子或没有左孩子的结点,其删除操作可以使用前面规定的方法完成。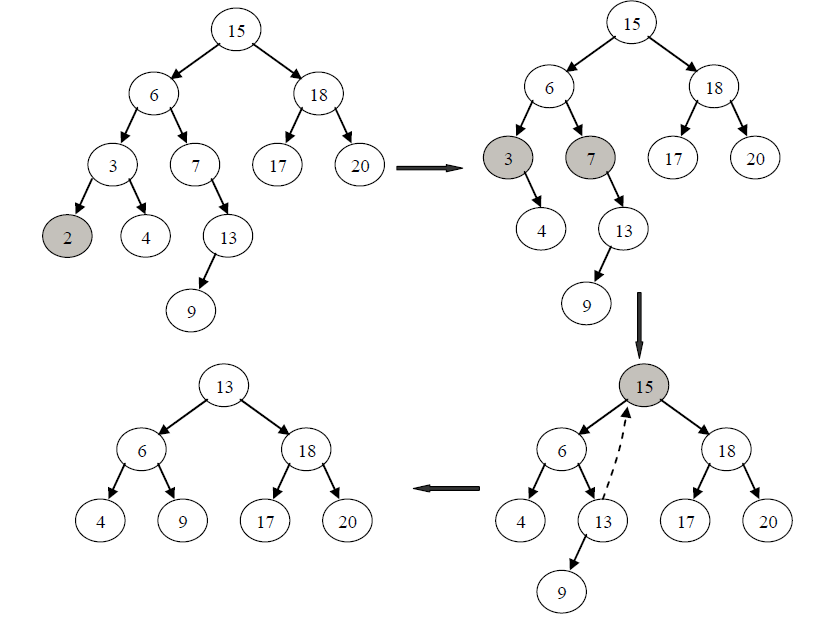
情况一举例:由于结点2 是叶子结点,则直接摘除即可。
情况2举例:例如在图所示的二叉查找树中删除结点3 和7,由于3 是左孩子,因此在删除结点3 之后,将其右子树设为其父结点6 的左子树即可;同样,因为7 是右孩子,因此在删除结点7之后,将其右子树设为其父结点6 的右子树即可。
情况3举例:例如在图所示的树中删除结点15,由于结点15既有左子树又有右子树,则此时,可以先找到其前驱结点13,并用13替换15,然后删除结点13即可。
public Object remove(Object ele) {
BinTreeNode v = (BinTreeNode) binTSearch(root, ele);
if (v == null)
return null; // 查找失败
BinTreeNode del = null; // 待删结点
BinTreeNode subT = null; // 待删结点的子树
if (!v.hasLChild() || !v.hasRChild()) // 确定待删结点
del = v;
else {
del = getPredecessor(v);
Object old = v.getData();
v.setData(del.getData());
del.setData(old);
}
// 此时待删结点只有左子树或右子树
if (del.hasLChild())
subT = del.getLChild();
else
subT = del.getRChild();
if (del == root) { // 若待删结点为根
if (subT != null)
subT.sever(); //断开与父亲的关系
root = subT;
} else if (subT != null) {
// del为非叶子结点
if (del.isLChild())
del.getParent().setLChild(subT);
else
del.getParent().setRChild(subT);
} else
// del为叶子结点
del.sever();
return del.getData();
}将数据元素构造成二叉查找树的优点:
①查找过程与顺序结构有序表中的折半查找相似,查找效率高;
②中序遍历此二叉树,将会得到一个关键字的有序序列(即实现了排序运算);
③如果查找不成功,能够方便地将被查元素插入到二叉树的叶子结点上,而且插入或删除时只需修改指针而不需移动元素。
总结:二叉查找树既有类似于折半查找的特性,又采用了链表存储,它是动态查找表的一种适宜表示。若数据元素的输入顺序不同,则得到的二叉查找树形态也不同。
附:全部代码
package dsa.adt;
import dsa.adt.BinaryTreeLinked;
import dsa.adt.SearchTable;
import dsa.strategy.Strategy;
import dsa.strategy.DefaultStrategy;
public class BSTree extends BinaryTreeLinked implements SearchTable {
protected BinTreeNode startBN; // 在AVL树中重新平衡的起始结点
// 构造方法
public BSTree() {
this(new DefaultStrategy());
}
public BSTree(Strategy strategy) {
this.root = null;
this.strategy = strategy;
startBN = null;
}
// 查询查找表当前的规模
public int getSize() {
return root == null ? 0 : root.getSize();
}
// 判断查找表是否为空
public boolean isEmpty() {
return getSize() == 0;
}
// 返回查找表中与元素ele关键字相同的元素位置;否则,返回null
public Node search(Object ele) {
return binTSearch(root, ele);
}
private Node binTSearchRe(BinTreeNode rt, Object ele) {
if (rt == null)
return null;
switch (strategy.compare(ele, rt.getData())) {
case 0:
return rt; // 等于
case -1:
return binTSearchRe(rt.getLChild(), ele);// 小于
default:
return binTSearchRe(rt.getRChild(), ele);// 大于
}
}
private Node binTSearch(BinTreeNode rt, Object ele) {
while (rt != null) {
switch (strategy.compare(ele, rt.getData())) {
case 0:
return rt; // 等于
case -1:
rt = rt.getLChild();
break;// 小于
default:
rt = rt.getRChild(); // 大于
}
}
return null;
}
// 返回所有关键字与元素ele相同的元素位置
public Iterator searchAll(Object ele) {
LinkedList list = new LinkedListDLNode();
binTSearchAll(root, ele, list);
return list.elements();
}
public void binTSearchAll(BinTreeNode rt, Object ele, LinkedList list) {
if (rt == null)
return;
int comp = strategy.compare(ele, rt.getData());
if (comp <= 0)
binTSearchAll(rt.getLChild(), ele, list);
if (comp == 0)
list.insertLast(rt);
if (comp >= 0)
binTSearchAll(rt.getRChild(), ele, list);
}
// 按关键字插入元素ele
public void insert(Object ele) {
BinTreeNode p = null;
BinTreeNode current = root;
while (current != null) { // 找到待插入位置
p = current;
if (strategy.compare(ele, current.getData()) < 0)
current = current.getLChild();
else
current = current.getRChild();
}
startBN = p; // 待平衡出发点
if (p == null)
root = new BinTreeNode(ele); // 树为空
else if (strategy.compare(ele, p.getData()) < 0)
p.setLChild(new BinTreeNode(ele));
else
p.setRChild(new BinTreeNode(ele));
}
// 若查找表中存在与元素ele关键字相同元素,则删除一个并返回;否则,返回null
public Object remove(Object ele) {
BinTreeNode v = (BinTreeNode) binTSearch(root, ele);
if (v == null)
return null; // 查找失败
BinTreeNode del = null; // 待删结点
BinTreeNode subT = null; // del的子树
if (!v.hasLChild() || !v.hasRChild()) // 确定待删结点
del = v;
else {
del = getPredecessor(v);
Object old = v.getData();
v.setData(del.getData());
del.setData(old);
}
startBN = del.getParent(); // 待平衡出发点
// 此时待删结点只有左子树或右子树
if (del.hasLChild())
subT = del.getLChild();
else
subT = del.getRChild();
if (del == root) { // 若待删结点为根
if (subT != null)
subT.sever();
root = subT;
} else if (subT != null) {
// del为非叶子结点
if (del.isLChild())
del.getParent().setLChild(subT);
else
del.getParent().setRChild(subT);
} else
// del为叶子结点
del.sever();
return del.getData();
}
// 返回以v为根的二叉查找树中最小(大)元素的位置
public Node min(BinTreeNode v) {
if (v != null)
while (v.hasLChild())
v = v.getLChild();
return v;
}
public Node max(BinTreeNode v) {
if (v != null)
while (v.hasRChild())
v = v.getRChild();
return v;
}
// 返回结点v在中序遍历序列中的前驱结点
private BinTreeNode getPredecessor(BinTreeNode v) {
if (v == null)
return null;
if (v.hasLChild())
return (BinTreeNode) max(v.getLChild());
while (v.isLChild())
v = v.getParent();
return v.getParent();
}
// 返回结点v在中序遍历序列中的后续结点
private BinTreeNode getSuccessor(BinTreeNode v) {
if (v == null)
return null;
if (v.hasRChild())
return (BinTreeNode) min(v.getRChild());
while (v.isRChild())
v = v.getParent();
return v.getParent();
}
}






















 461
461

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








